מוכיחים את הלא נודע

להוציא שורש של מספר ממשי זה קל. אולי לאדם קצת קשה לחשב במדוייק את שורש 2, אבל מחשב מסוגל לעשות זאת בשניות. יש טכניקות רבות לצורך כך, והחביבה עלי היא שיטת ניוטון-רפסון. כל מחשבון כיס מסוגל להוציא שורשים והפעולה הזו נראית לנו טבעית כמו ארבע פעולות החשבון הבסיסיות.

ועם זאת, אם אנו משנים את מערכת המספרים שלנו ועוברים מהמספרים הממשיים לאוסף השאריות מודולו n כאשר n הוא מכפלה של שני מספרים ראשוניים גדולים (אנסה להציג את הכל בצורה פורמלית בהמשך) הבעיה של הוצאת שורש הופכת לקשה הרבה יותר. עם זאת, העלאה בריבוע של מספר נותרת קלה מאוד לביצוע. כתוצאה מכך, יש לנו שתי פעולות שהאחת היא היפוכה של השניה, אבל בעוד כיוון אחד קל לביצוע השני קשה. זוהי “פונקציה חד כיוונית”, והיא אחד מהמושגים הבסיסיים והחשובים של הקריפטוגרפיה המודרנית.

למה זה טוב? הדוגמה הקלאסית היא פרוטוקול הזדהות. נניח שאני רוצה להתחבר למחשב מרוחק כלשהו ולקבל את הרשאות הגישה שלי. מן הסתם יהיה צורך בססמא כלשהי, אחרת כל אחד יהיה מסוגל להתחבר תחת שמי. ססמא פותרת את הבעיה; היא “סוד” שידוע רק לי ולא לאף אחד אחר, ולכן וידוא שאני אכן יודע אותו הוא וידוא שאני מי שאני מתיימר להיות.

מה הבעיות בססמא פשוטה? ראשית, המחשב שאני מתחבר אליו צריך לזכור אותה, ולכן לכאורה ניתן יהיה באמצעות חיטוט בקבצים שלו לאתר את הססמא. בפועל זו אינה בעיה; מה שנשמר על המחשב אינו הססמא אלא תוצאה של הפעלת פונקציה חד-כיוונית עליה. עוד דרישה מפונקציה חד-כיוונית היא שכמעט ולא יהיו “התנגשויות” בפונקציה - שני ערכים שממופים לאותה תוצאה - ולכן קל לבדוק שהתקבלה הססמא הנכונה (מפעילים עליה את הפונקציה ומשווים את התוצאה למידע השמור) אבל קשה לשחזר את הססמא המקורית גם אם מגלים את המידע השמור. למשל, במקרה שלנו הססמא תוכל להיות מספר כלשהו מודולו n, ומה שיהיה שמור במחשב הוא ריבוע המספר מודולו n.

אבל הבעיה השניה והחמורה בהרבה היא השאלה מה יישלח למחשב המרוחק. אם נשלח את הססמא עצמה יהיה קל למחשב לודא את נכונותה (כאמור, על ידי העלאה בריבוע והשוואה למספר ששמור אצלו תחת שמנו), אבל אז אנחנו לוקחים את הסיכון שכל מי שמצותת לקו התקשורת בינינו לבין המחשב (וההנחה היא שתמיד יש אויב מרושע שכזה) יצליח לשמוע את הססמא, ומעתה והלאה יוכל להעמיד פנים שהוא זה אנחנו.

לכן אנחנו צריכים קסם כאן: להיות מסוגלים לשכנע את המחשב שאנחנו יודעים את הססמא, מבלי שנגיד לו אותה. יותר מכך - אנחנו צריכים לשכנע אותו שאנחנו יודעים את הססמא מבלי שהדבר יחשוף, ולו ברמז, מהי הססמא הזו. הקסם שמקיים את התכונה הזו נקרא “הוכחה באפס ידע”.

מושג אפס הידע הוא מבלבל למדי. הכוונה אינה שבפרוטוקול כלל לא יועבר מידע (אחרת בשביל מה יש פרוטוקול), אלא שלא יתווסף למוודא שום ידע חדש - כש”ידע” פירושו “דברים שהמוודא (המוגבל פולינומית) לא מסוגל גם ככה לחשב בעצמו”. כך למשל להוכיח למישהו ש-1+1=2 פשוט על ידי כתיבת ההוכחה זו “הוכחת אפס ידע” כי המוודא ממילא מסוגל להגיע להוכחה בעצמו בלי קושי רב.

מכיוון שאנו פסימיים, אנחנו לא חוששים רק מציתות לפרוטוקול, אלא גם מכך שהגורם העויין יצליח להתחזות למחשב שאליו אנו מתחברים, וכך יהפוך בעצמו ל”מוודא” בפרוטוקול שלנו. על כן, דרישת אפס הידע תובעת שלא משנה מה יעשה המוודא, אנחנו כמוכיחים לא נוסיף לו ידע (בדומה לכך שדרישה סטנדרטית מפרוטוקול היא שלא משנה מה יעשה המוכיח, המוודא לא ישתכנע בנכונות שקר אלא בהסתברות נמוכה מאוד).

את הדיון הפורמלי יותר בכל זה, כמו גם הצגת מערכת ההוכחה הספציפית שמתאימה לבעיית הוצאת השורש, אציג בפוסט הבא. בינתיים אציג שתי דוגמאות קלאסיות ואינטואיטיביות יחסית להוכחות אפס ידע: בעיית “איפה אפי” ובעיית ה-3-צביעה של גרף.

“איפה אפי” (“Where’s Waldo” באנגלית) הוא גיבורה של סדרת ספרים שכל אחד מהם מורכב מתמונות רבות עמוסות באנשים, שבכל אחת מהן יש לאתר את אפי בתוך הקהל. אני אישית מעדיף את “ספר עולמי” וספרי “1000 מילים ראשונות” שיצאו בהוצאת מסדה פרס וא. קלין (מה קרה לספרים? מה קרה להוצאות? מתי יוציאו עוד ספרים כאלו?) שגם בהם היה צריך לחפש מישהו - כלב במקרה של ספר עולמי, ברווז וצפרדע במקרה של 1000 מילים ראשונות.

ובכן, נניח שיש לי תמונה של “איפה אפי”, גיליתי את אפי ואני רוצה להוכיח לכם שאני יודע איפה הוא - אבל מבלי שאגלה לכם איפה הוא מופיע בתמונה או אפילו אתן לכם רמז. בלתי אפשרי? מתברר שלא רק שאפשרי, גם קל למדי.

מה שעושים הוא כדלהלן: לוקחים דף נייר חלק וגדול מאוד (גדול בהרבה מהתמונה), חותכים במרכזו חור בגודל של אפי (כפי שאפי מופיע בתמונה המקורית). מבקשים מהמוודא להסתכל הצידה לרגע (אם הוא חושד שנחליף את התמונה באחת אחרת הוא מוזמן לבצע חיפוש גופני מלא עלינו), ואז שמים את הדף החלק על התמונה בצורה כזו שרק אפי מציץ מהחור שיצרנו. עכשיו קוראים למוודא.

מה המוודא רואה? רק נייר לבן שבמרכזו חור ובו אפי. כלומר, הוא מבין שהצלחנו למצוא את אפי בתמונה, אחרת לא היינו מצליחים להראות לו אותו דרך החור. עם זאת, אין לו מושג איפה בתמונה אפי נמצא, כי החלון לא מספק שום רמז כזה: רק אפי מופיע בו, ולא שום דבר מהסביבה שלו. בגלל שהנייר גדול בהרבה מהתמונה, גם אי אפשר לנחש באיזה איזור של התמונה אפי נמצא (מה היה קורה אם הנייר היה בדיוק בגודל התמונה?)

כמובן שיש שיטה אחרת להוכחה הזו והיא פשוט לגזור את אפי מהתמונה המקורית - אבל אנחנו מעדיפים שיטות פחות אלימות.

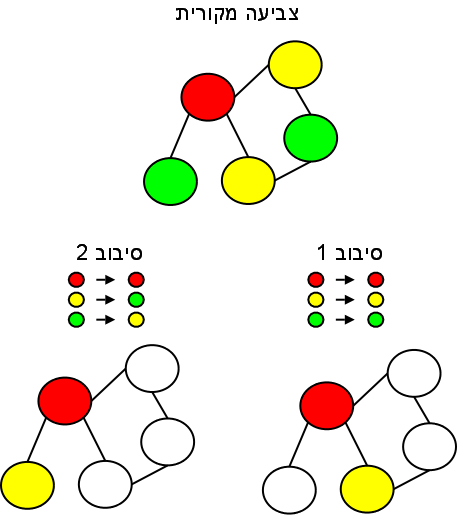
ומכאן - ל-3-צביעה של גרף. כבר הזכרתי את מושג הגרף בפוסט הקודם. צביעה של גרף היא פשוט צביעה של כל אחד מצמתי הגרף בצבע כלשהו, כשהאתגר הוא ששני צמתים שמחוברים בקשת לא יהיו צבועים באותו הצבע (אם זה לא מתקיים, הצביעה “אינה חוקית”). בעיית 3 הצביעה היא הבעיה הבאה: בהינתן גרף, יש לומר האם מספיקים 3 צבעים כדי לצבוע אותו צביעה חוקית, או לא (שאלה דומה, השאלה “האם בהינתן גרף שמייצג מפה תמיד מספיקים 4 צבעים כדי לצבוע אותו” הפכה למפורסמת מאוד, ואני מקווה לפרט עליה בעתיד).

מתברר שבעיית ה-3-צביעה הזו היא קשה למדי (קשה לבדוק את כל האפשרויות כי יש המון דרכים לצבוע גרף בשלושה צבעים - \( 3^n \) כאשר \( n \) הוא מספר הקודקודים - ולא מוכרת דרכים יעילות הרבה יותר לבדוק האם הגרף 3-צביע או לא) , ומצד שני היא גם חשובה למדי, כי פתרונה יגרור פתרון של המוני בעיות קשות דומות שניתנות ל”תרגום” אליה (היא מה שמכונה “בעיה NP-שלמה”). משמעות קיום הוכחת אפס ידע עבורה היא שקיימת הוכחה כזו עבור כל בעיה מהמחלקה NP שהזכרתי בפוסט הקודם (למעשה, יש הוכחת אפס ידע לכל בעיה שניתן להוכיח באמצעות הוכחה אינטראקטיבית מהסוג שראינו בפוסט הקודם, אך ההוכחה לכך מסובכת יותר).

ובכן, נניח שאני חכם והצלחתי לגלות 3-צביעה לגרף כלשהו. עכשיו אני רוצה להוכיח למוודא שהגרף אכן ניתן לצביעה בשלושה צבעים, אבל לא לגלות לו את הצביעה הזו או אפילו לתת לו רמז מה היא. איך אני עושה את זה?

הפרוטקול שלנו מורכב מסיבובים שבהם מתבצע בכל פעם אותו הדבר. בכל סיבוב לא נחשף למוודא שום מידע, ובכל זאת מובטח שאם הגרף 3-צביע, הוא לא ימצא רבב בהוכחה שלנו, ואם הגרף אינו 3-צביע, קיימת הסתברות חיובית וקבועה כלשהי שהוא יתפוס אותנו בקלקלתנו. כל סיבוב הולך כך:

ראשית, אנו בוחרים באופן אקראי פרמוטציה על הצבעים שלנו, וצובעים את הגרף בצורה דומה לצביעה המקורית שמצאנו, אך בהתאם לפרמוטציה. למשל, אם הפרמוטציה שלנו הייתה “ירוק עובר לאדום, אדום עובר לצהוב, צהוב עובר לירוק”, אז נצבע באדום כל צומת שבצביעה המקורית שלנו הייתה ירוקה, וכדומה (למה הצביעה עדיין חוקית?)

כעת נכסה את כל הקודקודים כך שלא ניתן יהיה לראות את צבעם, ונציג את הגרף המכוסה למוודא. המוודא יבחר באקראי שני צמתים שמחוברים בקשת. נסיר את הכיסוי משני הצמתים הללו. כעת קורה אחד משניים:

1. אם באמת הצביעה שלנו הייתה חוקית, הרי ששני הצמתים יהיו צבועים בצבעים שונים. בגלל שהגרלנו פרמוטציה על צבעי הצמתים, זה גם כל המידע שהמוודא יפיק - ששני הצמתים הללו צבועים בצבע שונה (וזה מידע שממילא יש לו כי כל שני צמתים המחוברים בקשת צריכים להיות צבועים בצבע שונה).
2. אם הצביעה שלנו אינה חוקית, אז יש שני צמתים שמחוברים בקשת שצבועים באותו הצבע. אם המוודא יבחר אותם באקראי, הלך עלינו. הסיכוי שהמוודא יבחר אותם הוא \( 1/k \), כאשר \( k \) הוא מספר הקשתות.

אם כן, התנאים מתקיימים. אמנם, נראה כי הסתברות של \( 1/k \) לגלות שקר היא עלובה למדי - אבל כמקודם, אם חוזרים על הפרוטוקול מספיק פעמים (כש”מספיק” פירושו “ממש לא הרבה ביחס לזמן שיקח לנו לבדוק את כל הצביעות האפשריות בעצמנו”), ההסתברות לטעות היא אפסית.

מכיוון שאפס-הידע הוא העיקר בפרוטקול הזה (בלעדיו, הוכחה אינטראקטיבית ל-3-צביעה היא קלה; פשוט שולחים את הצביעה) אני רוצה להתעכב שוב על טענת ה”המוודא לא לומד כלום” ולהמחיש אותה. נניח שבסיבוב אחד של הפרוטוקול חשפנו את צומת א’ וצומת ב’, וראינו שא’ צבוע אדום וב’ צהוב. בסיבוב שלאחר מכן חשפנו את צומת א’ וצומת ג’, וראינו שוב - א’ צבוע אדום, ג’ צהוב. האם למדנו מכך משהו? בפרט, האם למדנו שב’ ו-ג’ צבועים באותו הצבע?

התשובה היא שממש לא. ייתכן שבסיבוב הראשון הפרמוטציה שהגריל המוכיח הייתה “אדום->אדום, צהוב->צהוב, ירוק->ירוק” ובשני הייתה “אדום->אדום, צהוב->ירוק, ירוק->צהוב” ואז ב’ צבוע במקור בצהוב, וג’ בירוק והם שונים; אבל ייתכן שבסיבוב השני הוגרלה אותה פרמוטציה כמו בראשון, ואז ב’ וג’ שניהם צבועים במקור בצהוב והם זהים. בקיצור - המוודא לא לומד כלום, כי כל האפשרויות לצביעה אפשריות - פרט לאפשרות של “שני צמתים מחוברים בקשת צבועים באותו הצבע” (שאלת אתגר: למה המוודא חייב לבחור רק צמתים מחוברים בקשת? מה יקרה אם הוא יוכל לבקש מהמוכיח לחשוף גם צמתים שאינם מחוברים בקשת?).

ייתכן שתתהו איך מתבצעת בפועל ההסתרה של צמתי הגרף וחשיפתם. בצורה ידנית די ברור איך עושים זאת, אבל זו הוכחה איטית ומסורבלת. באמצעות מחשב הרבה יותר קשה לוודא שהמוכיח לא מרמה - צריך לוודא שברגע שהוא מציג את הגרף המכוסה למוודא הוא “מתחייב” על הצביעה שמוסתרת בו, ולא שהוא צובע את שני הצמתים שנבחרו ברגע האחרון, אחרי שהמוודא כבר בחר אותם. יש שיטות קריפטוגרפיות לעשות זאת, אך לא אכנס אליהן כרגע.

לסיכום, אני רוצה להזכיר לשם מה התכנסנו כאן - הוכחות לא קונסטרוקטיביות. לדעתי, ההוכחה ל-3-צביעות הגרף היא אחת מההוכחות הלא קונסטרוקטיביות היפות ביותר שאני מכיר. כאן האובייקט הוא לא מסובך, לא דרושות אקסיומות בחירה שונות ומשונות כדי לקבל אותו, ואנחנו זוכים לראות חלקים ממנו שוב ושוב ושוב. יותר קרוב מזה לקונסטרוקטיביות אי אפשר - ועם זאת, עדיין אין לנו שום מושג מהו. אפס מוחלט.