האם מכונות טיורינג חולמות על ריצופים של רבע המישור?

למרות שטרחתי להציג את המודל של מכונת טיורינג בפוסטים קודמים, טרם נתתי דוגמה קונקרטית לנוחות שנובעת מכך שהתיאור שלה הוא פשוט כל כך. אני מקווה לתקן את המעוות כעת, עם הרדוקציה מבעיית העצירה לבעיה של ריצוף רבע המישור באמצעות אריחי וונג, כשהפינה השמאלית-תחתונה נתונה.

נתחיל מזה שלא באמת נבצע את הרדוקציה מבעיית העצירה, אלא מבעיה קצת יותר “פשוטה” - הבעיה הבאה: בהינתן מכונת טיורינג, צריך להכריע האם היא עוצרת על הקלט הריק או לא. לכאורה, זה מקרה פרטי של בעית העצירה, ולכן אולי כריע; בפועל, אפשר לבצע בקלות רדוקציה מבעית העצירה אליו: בהינתן מכונה \( M \) וקלט \( x \) משתמשים בתעלול ה”סינון” שכבר ראינו במשפט רייס, בונים מכונה \( M_x \) שמריצה את \( M \) על \( x \) ורק אחרי שהריצה הסתיימה (אם היא הסתיימה) מתפנים להתעסק עם הקלט ה”אמיתי” של המכונה - בואו נניח שפשוט עוצרים תמיד. לכן, אם אלגוריתם שפותר את הבעיה “הפרטית” אומר על \( M_x \) שהיא עוצרת, אז \( M \) עוצרת על \( x \); ואם לא, אז לא.

עכשיו, לרעיון המרכזי של הרדוקציה - אנחנו רוצים להשתמש בריצוף כדי לבצע סימולציה של ריצת מכונת הטיורינג הנתונה על הקלט הריק. אנחנו רוצים שאם יהיה ריצוף אינסופי לרבע המישור, נוכל להביט בריצוף ו”לתרגם” אותו לריצה אינסופית של מכונת הטיורינג - ומכאן המסקנה הפשוטה, שהמכונה עוצרת על הקלט הריק אם ורק אם לא קיים ריצוף לרבע המישור כשהפינה ההיא נתונה.

אם כך, אנחנו רוצים להשתמש בריצוף כדי לתאר ריצה של מכונת טיורינג. לשם כך, צריך קודם כל למצוא דרך מתמטית לתאר ריצה, ובפרט את שלבי הריצה. לשם כך משתמשים במושג של קונפיגורציה. קונפיגורציה (“תיאור רגעי”?) היא כל המידע הנחוץ לתיאור שלב מסויים של ריצת מכונת הטיורינג. כאן “נחוץ” זה רק המידע שהכרחי על מנת לדעת מה יהיה הצעד הבא של המכונה; אפשר לחשוב על עוד נתונים מעניינים (כמה זמן עבר מאז תחילת הריצה, למשל) שלא נכללים בו. המושג רלוונטי גם למחשבים אמיתיים; למשל, תוכנות האמולציה בדרך כלל מציעות אפשרות של “שמירת מצב” ששומרת במדויק את מצב המכונה, כולל הזיכרון והאוגרים הפנימיים, ובכך מאפשרת לשחזר במדוייק את אותה נקודת זמן במהלך הריצה גם בעתיד (ובפרט, לתת אפשרות שמירת משחקים נוחה מאוד).

ממה מורכבת קונפיגורציה של מכונת טיורינג? ראשית, כל תוכן הסרט (כולל התאים הריקים). מכיוון שהסרט אינסופי, גם התוכן אינסופי. באופן עקרוני, בכל נקודת זמן אפשרית רק חלק סופי מהסרט תפוס על ידי קלט ואינו ריק, ולכן אפשר לייצג את התוכן באמצעות ייצוג סופי - כאן דווקא הייצוג האינסופי יותר טוב לנו, כפי שנראה עוד מעט.

שנית, יש עוד שני נתונים הכרחיים - מיקום הראש הקורא על פני הסרט, והמצב הפנימי שבו מכונת הטיורינג נמצאת. מי שיודע את כל המידע הזה יודע במדוייק לא רק מה יהיה הצעד הבא של המכונה, אלא גם איך תיראה הקונפיגורציה הבאה.

נותר לחשוב על דרך קומפקטית לכתוב את הקונפיגורציה. קצת מצחיק לומר “קומפקטית” בהתחשב בכך שמה שנכתוב יהיה אינסופי באורכו, אבל המוטיבציה כבר מתחילה להתבהר - אנחנו רוצים שהריצוף ייצג סדרת קונפיגורציות של ריצת מכונת הטיורינג. דרך אפשרית אחת היא שכל שורה תייצג קונפיגורציה, ושתי שורות סמוכות יהיו חוקיות מבחינת הריצוף אך ורק אם מהקונפיגורציה שמייצגת השורה הנמוכה יותר אפשר להגיע בצעד אחד לקונפיגורציה שמייצגת השורה הגבוהה יותר. אם כן, אנחנו רוצים לייצג את התוכן של הסרט באמצעות אריחי וונג, ואיכשהו לדחוף פנימה, מקודד באמצעות אריחים, גם את מיקום הראש הקורא והמצב הפנימי של המכונה.

הטריק הוא פשוט יחסית - קונפיגורציה היא סדרה של תווים מהסוג שיכול להופיע על הסרט (במקרה שלנו אנחנו מסתפקים בשלושה - 0, 1 ו”ריק”). בנוסף לכך, עבור האיבר בסדרה שמייצג את התא שהראש הקורא נמצא בו כרגע, יהיה סימון נוסף - סימון עבור המצב שבו נמצאת המכונה.

כך למשל הקונפיגורציה “תוכן הסרט מתחיל ב-010110 ואחר כך רק תאים ריקים, הראש הקורא נמצא בתא השלישי והמכונה נמצאת במצב הפנימי p” תתואר באופן הבא:

\( 0,1,(0,p),1,1,0,\flat,\dots \)

אפשר להגדיר כעת בצורה פורמלית מתי קונפיגורציה אחת נובעת מהשניה - אשאיר זאת כתרגיל למי שמתעניין בהיבטים הפורמליים של העסק (שבסופו של דבר, הם הכרחיים).

אם כן, מתווה הדרך שלנו ברור. יהיו אריחים כדי לתאר את האיברים 0, 1 ו”תא ריק” בסדרה. בנוסף, יהיו אריחים נוספים שמסוגלים לתאר זוגות של תו ומצב, ושולטים על השינוי שהמכונה תבצע בקונפיגורציה. אפשר לעשות את כל זה עם מספר סופי של סוגי אריחים, מכיוון שמכונת הטיורינג ניתנת לתיאור באמצעות פונקצית מעברים סופית.

רק רעיון עקרוני אחרון - כל אריח מייצג לא קונפיגורציה אחת, כי אם שתיים; התו שמצוייר על חלקו התחתון מתאר את הקונפיגורציה הראשונה, והתו שמצוייר על חלקו העליון מתאר את הקונפיגורציה השניה, שנובעת ממנה.

וכעת, לבניה עצמה - לאוסף האריחים שנבנים בהינתן מכונת טיורינג שרוצים לבדוק.

נתחיל מהשורה הראשונה. היא מיוחדת, מכיוון שצריך איכשהו “לאתחל” את המכונה - להכריח את הסרט כולו להיות ריק ואת הראש הקורא להיות בהתחלה. מספיקים שני סוגי אריחים בשביל זה:

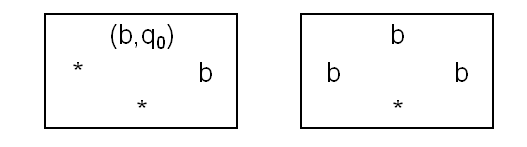ראשית, שימו לב לדרך המשונה שבה אני מתאר אריח. במקום צבעים, אני כותב סימנים על הצדדים של הריבוע (שהפך אצלי למלבן). כמובן שזה לא משנה כלום - כל עוד אני אשתמש רק במספר סופי של סימנים (וזה מה שאעשה), אפשר לקודד כל סימן באמצעות צבע, וכו’. כרגיל בחישוביות, בעיות ייצוג שכאלו הן ממש לא רלוונטיות.

האריח השמאלי הוא האריח החשוב ביותר כאן; זה האריח שאנו דורשים שיהיה בפינה השמאלית התחתונה, זה שמתחיל את הכל. הצד העליון שלו אומר שבקונפיגורציה שהוא מייצג, המכונה נמצאת במצב ההתחלתי (\( q_0 \)) בתא הראשון, ושהתא הזה ריק (סימנתי “ריק” באמצעות b, מלשון blank). ה-b שנמצא בצד ימין מטרתו לאפשר אך ורק לאריחים מהסוג השני שציירתי כאן להתחבר אליו; לא יהיו עוד אריחים שכתוב b על הצד השמאלי שלהם. האריח השני מטרתו “לאתחל” את שאר הסרט להיות ריק גם כן; החשיבות שלו בכך שעל צידו העליון כתוב רק b, כלומר הוא מייצג תא ריק (וכזה שהראש אינו עליו) בקונפיגורציה.

נסו לשחק קצת עם המלבנים ולחשוב איך תיראה השורה הראשונה בריצוף שמשתמש רק בהם ושם את האריח השמאלי בקצה השמאלי של השורה. עכשיו קיראו ברצף את התווים שעל החלק העליון של האריחים - תקבלו בדיוק את הסדרה עליה אנו רוצים לחשוב כעל קונפיגורציה התחלתית:

\( (b,q_0),b,b,b,\dots \)

טוב, עכשיו לשאר הקונפיגורציות. מקונפיגורציה אחת עוברים לשניה בצורה די פשוטה - כל תו שלא בסביבה המיידית של הראש הקורא פשוט “מפעפע” הלאה לקונגפיגורציה הבאה:

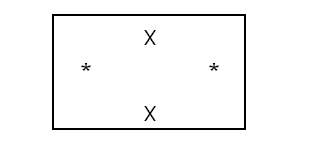כאן הצגתי “אב-טיפוס” של אריחים - צריך להחליף את ה-x בתווים קונקרטיים - במקרה שלנו 0,1, או b. שימו לב שכעת משתמשים בכוכביות בתור אמצעי החיבור (ולכן הברנש הזה לא מסוגל להתחבר לשורה התחתונה). עוד דבר שמעניין לשים אליו לב הוא שהברנש הזה, אם ניתן לו לפעול לבדו, מסוגל לרצף את כל רבע המישור בעצמו (איך?) ולכן זה הכרחי שנדרוש את הפינה השמאלית התחתונה כפי שדרשנו. אם יש את הפינה הזו, האריח הזה לבדו לא מסוגל לעשות שום דבר, כי הוא אינו מתאים לסימני השפה שמציינים “הראש הקורא כאן” (והם, כזכור, מהצורה (x,q) כש-x הוא תו ו-q הוא מצב).

מה נשאר? לתאר מה קורה בסביבתו של הראש הקורא. לצורך פשטות אפשר להניח שהוא חייב תמיד לזוז ימינה או שמאלה, ושבריצה שלו הוא אף פעם לא “נופל” מהסרט (כלומר, מנסה לצעוד שמאלה כשהוא כבר כך בקצה השמאלי של הסרט). אלו הגבלות על המודל שעדיין נותנות מכונה שקולה בכוחה - זה תרגיל לא רע (אם כי די משמים) להוכיח זאת.

גם כאן אני לא מציג אריחים קונקרטיים, אלא רק את התבנית הכללית לייצור אריחים - וייתכן שבשיטה הזו יווצר מספר גדול של אריחים. העיקר הוא שהמספר יהיה סופי - והוא יהיה סופי כי יש רק מספר סופי של מעברים בפונקצית המעברים של המכונה.

אם כן, יהיה מעבר כלשהו \( \delta(q,x)=(p,y,R) \). משמעות מה שכתבתי כאן הוא “אם אתה במצב הפנימי q ורואה את האות x, עבור למצב הפנימי p, כתוב y על הסרט, והזז את הראש הקורא צעד אחד ימינה”. כאן x,y הם סימן כלשהו מהשפה: ייתכן למשל ש-x=0 ואילו y=b ואז, כשרואים 0, מרוקנים את התא בסרט.

והנה שני האריחים שצריך כדי למדל את הפעולה הזו:

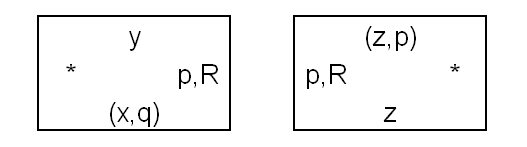מה קורה כאן? אם בשורה הקודמת הקונפיגורציה הכילה את (x,q), הרי שהאריח במקום המתאים לראש הקורא הכיל (x,q) על הצד העליון שלו. בדיוק אל ה-(x,q) הזה האריח השמאלי מתחבר. שימו לב לשינוי שמתרחש בקונפיגורציה בתוך האריח הזה - הצד העליון שלו מכיל את y לבד. כלומר, הראש הקורא כבר לא עמנו, והתו שהיה קודם x הפך ל-y.

לאן הראש הקורא הולך? ימינה. לכן נכנס הסימן שעל צדו הימני של האריח לפעולה. הוא מכיל שני פרטי מידע: הראשון, שהראש זז ימינה (ולכן כתוב שם R), והשני, שהמכונה עוברת למצב p. כעת, הדברים היחידים שיודעים להתחבר לאריח שמצד ימין שלו יש סימן שכזה הם כאלו שבהם אותו הסימן מופיע על הצד השמאלי - ואלו בדיוק האריחים שמתוארים בצד הימני של האיור. מה שהם עושים הוא ברור למדי - הופכים את מה שהיה z בקונפיגורציה הקודמת ל-(z,p) - כלומר, אותו הדבר (אין שינוי בתו), בתוספת הראש הקורא וההימצאות של המכונה במצב p.

מבלבל? ייתכן מאוד. זו מהרדוקציות שהכברת מילים רק מסבכת אותן עוד יותר - הדבר הפשוט ביותר לעשותו הוא להסתכל על האיורים של האריחים, לחשוב איך הם יכולים להתחבר אחד לשני, ומה זה אומר על הקונפיגורציות שהם מייצגים (זכרו - כל שורה היא קונפיגורציה).

האם נותרו עוד אריחים? כן, אבל רק כאלו שמטפלים בתזוזה שמאלה של הראש הקורא במקום ימינה. דרך סבירה לבדוק האם הרדוקציה ברורה היא לחשוב כיצד האריחים הללו אמורים להיראות. זהו, נגמרה הרדוקציה. להוכיח שהיא “עובדת” לא אוכיח כאן; אני לא מנסה להיות מדויק.

אם כן, מבעיית העצירה - משהו שנראה “מנותק” למדי, מכיוון שמכונות טיורינג לא קיימות בעולם הפיזי - הגענו להוכחת אי כריעות של משהו שונה לגמרי (טוב, לא לגמרי; כפי שראינו, הקשר בינו לבין מכונות טיורינג די ישיר), שבניסוחו המקורי אין שום צל ורמז למכונות טיורינג. כמובן שזה לא הסוף לבעיות לא כריעות שאינן עוסקות ישירות במכונת טיורינג - הבעיה העשירית של הילברט, שכבר הזכרתי כאן, היא דוגמה בולטת, וגם בעיית המילה מתורת החבורות, שעליה טרם דיברתי, היא דוגמה בולטת נוספת. אני מקווה בעתיד לחזור לבעיות הללו יותר בפירוט.