כמה מעלות טובות לרדיאן עלינו

אחד מהחיפושים שהוביל נפש תועה לשווא אל הבלוג הזה היה “כמה מעלות אלגברה פאי”. הניחוש שלי הוא שפשר השאלה הוא איך פאי, ברדיאנים, מתרגם למעלות. זה תירוץ מצויין לדבר קצת על מהם רדיאנים ולמה פתאום, באמצע הלימודים הבית ספריים, מפסיקים להשתמש במעלות ועוברים לדבר עליהם. לשם כך קודם כל צריך לדבר על מה שבכלל מודדות הן מעלות והן רדיאנים - זווית. זו אולי נראית שאלה פשוטה ומטופשת, אבל מהי בעצם זווית?

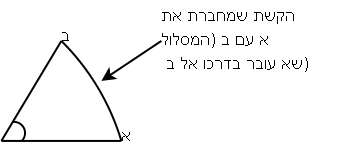
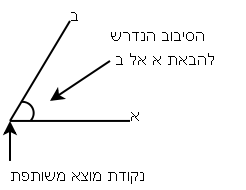הדרך הטובה ביותר שאני מכיר לתאר זווית היא פשוט בתור “כמות סיבוב”. נהוג לחשוב על זה כך: קחו שני קווים ישרים בעלי נקודת התחלה משותפת ואותו אורך (פורמלית קוראים לשני דברים כאלו “קטעים”, כי קו הוא אינסופי, אבל מה זה חשוב). ה”זווית” שבין שני הקווים היא כמות הסיבוב שנדרשת כדי להניח אחד מהם על השני. תכף ומייד מתברר שההגדרה הזו היא מה שמכונה במתמטיקה “לא מוגדרת היטב”, פשוט כי יש שתי דרכים לסובב את הישרים כך שיונחו אחד על השני - הדרך הקצרה והדרך הארוכה (אורך שתיהן שוות רק כששני הקווים פונים לכיוונים מנוגדים). מכאן שכל שני קווים מגדירים שתי זוויות ולא אחת.

אם כן, זוהי זווית, אבל כדי למדוד אותה יש צורך ביחידות (אי אפשר להגיד “סיבוב קצר”, “סיבוב קצת יותר גדול” וכדומה). בשביל לעשות זאת, רצוי להתחיל מסיבוב “מלא” (לוקחים קו; מסובבים אותו סביב ציר שנמצא באחת מנקודות הקצה שלו, עד שהוא חוזר למקום שבו היה בהתחלה; מודדים את כמות הסיבוב שנדרשה לשם כך) ולהגיד כמה יחידות הוא מכיל. על פניו, הגדרה “טבעית” תהיה להגיד שסיבוב מלא הוא יחידה אחת, כלומר 1, ולכן רבע סיבוב (שיוצר את מה שמכונה “זווית ישרה”) יהיה בגודל 1/4, וכן הלאה. זה לא רעיון מופרך, אך לא משתמשים בו.

מה שכן משתמשים בו, לפחות בהתחלה, הוא מעלות. לסיבוב המלא נותנים שרירותית את הגודל 360 מעלות, ואז זווית ישרה תהיה בת 90 מעלות, למשל. למרות שזו החלטה שרירותית לכאורה, יש בה הגיון רב. היא ככל הנראה נובעת מהבבלים הקדמונים, שהייתה להם חיבה למספר 60 (הוא היה בסיס מערכת הספירה שלהם, שהייתה מתקדמת מאוד לזמנה), וייתכן מאוד שהושפעה מכך שיש 365 ימים בשנה. היתרון הברור של 360 על פני 1 הוא שאת 360 אפשר לחלק בהמון דרכים שונות, ולכן לתת ייצוג מספרי פשוט (במספרים שלמים, במקום בשברים) להמוני זווית קטנות שהן שבר פשוט של סיבוב שלם (\( 360=2^33^25 \) ולכן אפשר לייצג במעלות שלמות דברים כמו “חצי סיבוב”, “רבע סיבוב”, “שמינית סיבוב”, “שליש סיבוב”, “תשיעית סיבוב”, “חמישית סיבוב”, “עשירית סיבוב”, וכדומה). למעשה, אפשר לקבל אישוש כלשהו לכמה השיטה הזו מוצלחת בכך שעד היום אנחנו משתמשים בה למרות שהמספרים שלה אינם “טבעיים” כמו כפולות של 10, ובוודאי שאינם “טבעיים” כמו הרדיאנים שתכף אציג.

אם כן, במשך רוב שנות בית הספר, ובפרט בלימודי הגאומטריה האוקלידית, משתמשים במעלות ותו לא. גם בחיי היום יום משתמשים במעלות. הרדיאנים צצים לראשונה בדרך כלל רק כשהתלמידים מגיעים ללימודי החשבון הדיפרנציאלי והאינטגרלי. רק על עצמי לספר ידעתי: כשלימדו אותי את המושג לראשונה, לא הבנתי כלום. בפרט לא הבנתי למה צריך אותו ואיך מגיעים אליו. כל מה שהבנתי הוא את נוסחת המעבר ממדידה במעלות למדידה ברדיאנים, וגם אותה שכחתי כל הזמן. מה לעשות - אחרי שמתרגלים למעלות, מדידה באמצעות פאי נראית לא טבעית בעליל. האתגר הקשה של הצגת הרדיאנים הוא המוטיבציה לקיומם; אומרים שהם “טבעיים”, ומצד שני, קשה להסביר למה למישהו שטרם למד חשבון דיפרנציאלי. אעדיף קודם להציג אותם ורק אחר כך להגיע לנימוק בדיוק מסיבה זו - כדי שגם מי שטרם נתקל בחשבון דיפרנציאלי יוכל לפחות להבין על מה מדובר כשמדברים על רדיאנים.

הצעתי קודם שיטה אחרת למדידה - לוקחים את “הסיבוב המלא” בתור 1. מהו “הסיבוב המלא” המדובר? אם מסתכלים על נקודת הקצה השנייה של הקו הישר שמסובבים, רואים שכאשר מסובבים אותו סיבוב מלא, הוא יוצר מעגל (תזכורת לשונית קטנה - מעגל הוא כל הנקודות שנמצאות על שפת הצורה שנוצרת. עיגול הוא גם ה”בפנוכו” של הצורה הזו). כאשר מסובבים אותו סיבוב חלקי, הוא יוצר חלק ממעגל - מה שמכונה “קשת” (Arc). כעת, למעגל כבר קיימים שני גדלים מדידים שמשוייכים אליו - הרדיוס שלו, והיקפו. הרדיוס של מעגל הוא מרחק הנקודות של המעגל מנקודת המרכז שלו. מכיוון שנקודת המרכז שלנו היא אחת מקצוות הישר שמסובבים, וכל נקודה על המעגל נמצאת על קצהו השני של הישר, הרדיוס במקרה הזה הוא אורכו של הישר שמסובבים. כעת, היקף המעגל תלוי ברדיוס - מן הסתם מעגלים בעלי רדיוס גדול יותר יהיו בעלי היקף גדול יותר - אך בכל זאת הוא קבוע במובן מסויים - היחס שלו ושל הרדיוס הוא מספר קבוע (למיטב זכרוני, ההוכחה נובעת מתכונות דמיון משולשים, בנוסף להגדרה המדוייקת של “היקף”, אך לא ניכנס לכך בינתיים). כלומר, אם מגדילים את הרדיוס של מעגל פי 2, גם היקפו גדל פי 2. זהו קשר פשוט ונאה מאוד. כדי שאפשר יהיה לקשר את הרדיוס וההיקף באמצעות נוסחה פשוטה כדאי לתת סימון לקבוע של היחס בין ההיקף והרדיוס; בפועל, ניתן סימון לקבוע של היחס בין ההיקף וקוטר המעגל (קוטר המעגל הוא אורך כל ישר שמחבר שתי נקודות על המעגל ועובר דרך המרכז - אורכו הוא פעמיים הרדיוס). הסימון הזה הוא פאי, \( \pi \). בשל כך, מתקיים הקשר הבא בין הרדיוס \( r \) ובין ההיקף \( c \): \( c=2\pi r \).

איך זה מתקשר לרדיאנים? ובכן, הלך המחשבה הוא זה: במקום להגדיר שרירותית את גודל הסיבוב של “מעגל שלם” בתור המספר 1 או המספר 360, אפשר להשתמש בגודל “טבעי” שכבר קיים עבורו - היקפו. הבעיה היא שההיקף, כאמור, אינו קבוע ותלוי ברדיוס המעגל. אם כן, כדי לקבל מספר קבוע, מגדירים את גודל הסיבוב של “מעגל שלם” בתור היקפו חלקי רדיוסו - מקבלים שגודל הסיבוב הזה הוא המספר \( 2\pi \).

כעת יש לנו גם אפשרות למדוד זוויות אחרות: באופן כללי, כשנתונה לנו זווית באמצעות שני ישרים שווי אורך, מהסוג שתיארתי קודם, אפשר לחשב את אורך הקשת שמחברת אותם (במובן מסויים זהו המרחק שהישר הראשון צריך לעבור עד שיגיע אל הישר השני - שכן הוא נע בסיבוב ולא בצורה ישרה, ולכן הקו הישר שמחבר בין שתי קצוות הישרים אינו המרחק האמיתי ביניהם) ולחלק באורכם. לרוב כדי להימנע מכל החלוקה הזו, פשוט מגדירים את הזווית באמצעות שני ישרים שאורכם 1. ה”יחידות” של אופן המדידה הזה נקראות “רדיאנים” - אבל למעשה, אלו אינן יחידות שרירותיות; מכיוון שאפשר להגדיר את הרדיאן בצורה פורמלית בתור אורך חלקי אורך (אורך הקשת חלקי אורך הישר שמסובבים), היחידות הן של מספרים “טהורים” - מה שמכונה בפיזיקה “גודל חסר ממד” (כלומר, שאינו תלוי במערכת המדידה שלנו). יתר על כן, הצלחנו לקשר את הכמות שמתארת זווית לכמות שמתארת מושג מרכזי עוד יותר - אורך, ולכן הרדיאנים הם אכן יחידות “טבעיות”. את היתרון של ה”טבעיות” הזו אראה בפוסט הבא.

הקשר בין מעלות לרדיאנים הוא, בתקווה, קצת יותר ברור כעת: אם במעגל יש 360 מעלות (שמסומנות \( 360^\circ \)) ו-\( 2\pi \) רדיאנים, אז מתקיים הקשר \( 2\pi=360^\circ \). לכן, מעלה אחת היא \( \frac{\pi}{180} \) רדיאנים, ואילו רדיאן אחד הוא \( \frac{180}{\pi} \) מעלות. בפרט, בתשובה לשאלה שפתחה את הדיון הזה, פאי רדיאנים הוא בדיוק 180 מעלות.

ומה על המוטיבציה? ובכן, אני מתכנן לזרוק לחלל האוויר בפוסט הבא את סינוס וקוסינוס, ואת הגבול \( \lim_{x\to 0} \frac{\sin(x)}{x}=1 \), ואולי גם טיפה טורי פורייה; אבל אשמח לשמוע עוד דוגמאות למקומות שבהם נוח להשתמש ברדיאנים ולא במעלות (וגם אשמח לראות הוכחה פורמלית לכך שפאי קבוע, אם כבר מדברים על כך, או הפניה לספר שמוכיח זאת).