“הוא חיפש על העץ…”

יש שתי גישות אפשריות לעיסוק בגרפים; האחת היא לחשוב על הגרף כעל יצור מתמטי אבסטרקטי ולנסות לחקור אותו - מה התכונות שלו, ואיזה אלגוריתמים בודקים אותן בצורה יעילה. משפט אוילר שעליו דיברתי בפוסט שעבר הוא דוגמה לאופן פעולה זה. הרעיון בגישה זו הוא שידוע לנו שגרף הוא אבסטרקציה שניתן להחיל על אלף ואחד דוגמאות שונות, ולכן אם פתרנו בעיה עבור גרף, פתרנו אותה גם עבור כל הדוגמאות הללו “בבת אחת” - ובחלקן ייתכן מאוד שלבעיה יש חשיבות. בפוסט הקודם ראינו שיש לפתרון של בעיית המסלולים האוילריאניים חשיבות הן לשאלה של צורות שאפשר לצייר מבלי להרים את הדף מהנייר, והן לשאלה של טיול שעובר בכל גשר בדיוק פעם אחת.

הגישה השנייה היא זו שמנסה להשתמש בגרפים לא בתור אבסטרקציה לכלום אלא בתור אובייקט מתמטי עם חיים משל עצמו, וליצור גרפים “מועילים”. הדוגמאות הבולטות ביותר לגישה זו הן של העצים השונים והמשונים שבהם משתמשים במדעי המחשב - וכדי להציג אותן, כדאי ראשית כל להגדיר את המושג של “עץ”. לפני ההגדרה הפורמלית, הגדרה לא פורמלית: עץ הוא גרף שנראה כמו אילן יוחסין. הגדרה פורמלית לעץ (לא מכוון) היא “גרף קשיר וחסר מעגלים”. בפועל, עץ הוא גרף שנראה, למשל, כך:

כלומר, הוא מורכב ממספר “ענפים” ש”מתפצלים” שוב ושוב (למרות שגם “שרוך” אחד ארוך נחשב עץ). הרעיון הבסיסי בעץ הוא שבין כל שני צמתים שבו מחבר מסלול אחד ויחיד. מכאן שאם נבחר צומת “בסיסי”, אפשר לחשוב על כל שאר העץ כצמתים שאליהם מגיעים על ידי מסלולים שיוצאים מאותו צומת בסיסי. לצומת הזה קוראים “שורש”. אם לוקחים עץ לא מכוון ורוצים לכוון אותו, בוחרים צומת שישמש כשורש, ומכוונים את הקשתות בצורה שתשמר את העובדה שלכל צומת ניתן להגיע מהשורש - כלומר, אם במסלול שיוצא מהשורש אל הצומת B מגיעים אליו מהצומת A, אז הקשת שבין A ו-B תכוון מ-A אל B. בסופו של דבר מגיעים לצמתים שרק אפשר להיכנס אליהם, לא לצאת - צמתים כאלו נקראים “עלים” (נסו לחשוב מדוע לעלה נכנסת רק קשת בודדת ולא כמה).

ישנה סדרה של תכונות שקולות שמגדירות עץ, ועוזרות לתת אינטואיציה לגביו. הנה כמה מהן - נסו לחשוב מדוע בכל עץ הן מתקיימות, ומדוע אם הן מתקיימות, הגרף הוא עץ:

• גרף קשיר שכל הסרת קשת ממנו תהפוך אותו ללא-קשיר.
• גרף חסר מעגלים שכל קשת שנוסיף לו תהפוך אותו לבעל מעגל.
• גרף קשיר עם n צמתים ו-n-1 קשתות (כאן אנו מניחים שהגרף בעל מספר סופי של צמתים - ישנם שימושים מתמטיים שבהם יש משמעות גם לגרפים אינסופיים).
• גרף חסר מעגלים עם n צמתים ו-n-1 קשתות.

כעת לשימוש בסיסי: עץ חיפוש. לפני כן צריך להסביר איך בכלל מבצעים חיפושים כשיש לנו אוספי מידע. בגישה הפשוטה ביותר, אפשר לחשוב על המידע שלנו בתור סדרה של פריטים, שלכל אחד יש “מספר מזהה” ייחודי משל עצמו. למספר כזה קוראים “מפתח” (באופן כללי המפתח לא חייב להיות מספר, אבל נוח לרוב להניח שהוא מספר או לפחות ניתן לתרגם אותו למספר כך שלשני מפתחות שונים יתאימו מספרים שונים).

כשבאוסף הפריטים שלנו אין בכלל סדר, הדרך היחידה לחפש בו איבר (כלומר, מישהו עם מפתח ספיציפי) היא לעבור על כל הפריטים שבו ולבדוק אותם; כי אם אין סדר, אז לא משנה כמה פריטים כבר בדקנו, תמיד ייתכן שהאחד שאנחנו מחפשים הוא זה שטרם בדקנו. סיבוכיות זמן הריצה של החיפוש הזה היא אם כן לינארית במספר הפריטים - תכפילו את מספר הפריטים פי 2, וזמן הריצה יגדל פי 2. האם יש דרך יעילה יותר?

מסתבר שסידורים שונים של הפריטים יכולים לשפר מאוד את יכולת החיפוש שלנו. שיטות אחסון יעילות שכאלו הן אחד מהנושאים הבסיסיים והמרכזיים ביותר בתחום במדעי המחשב שעוסק במבני נתונים. לעתים קרובות סוג מבנה הנתונים שבו משתמשים תלוי בתכונות של המידע שאותו רוצים לאחסן; כאן אדבר רק על שיטת אחסון פשוטה עבור מידע “כללי” (כלומר, כזה שמאופיין רק על ידי המספר המזהה, ומה שרוצים לעשות איתו הוא רק למצוא אותו).

אם הנתונים ממויינים כך שהמספרים הסידוריים שלהם רצים מהקטן אל הגדול, אז ניתן לבצע חיפוש בסיבוכיות לוגריתמית - כלומר, אם מכפילים את כמות הפריטים פי 2, זמן החיפוש יגדל רק ב-1 (לא יוכפל). שיטת חיפוש שכזו לדוגמה היא “חיפוש בינארי”. הרעיון הוא כזה: בדוק את האיבר האמצעי ברשימת הפריטים; אם הוא מי שחיפשנו, אחלה. אחרת, השווה את המספר הסידורי שלו למספר הסידורי שאנחנו מחפשים. אם המספר שאנחנו מחפשים גדול יותר, בדוק את האיבר האמצעי בחצי הרשימה שמכילה את כל הפריטים שמספרם גדול יותר מהאיבר האמצעי; אחרת, בדוק את האיבר האמצעי החצי הרשימה שמכילה את הפריטים שמספרם קטן יותר.

האלגוריתם הזה מצמצם את גודל רשימת הפריטים שבה הוא מחפש בחצי כל סיבוב, כשכל סיבוב דורש רק קריאה אחת, ולכן מספר הקריאות הכולל יהיה לוגריתמי בגודל הרשימה. יש רק בעיה אחת עם האלגוריתם, שהיא בחצי הדרך שבין תיאוריה ופרקטיקה - איך בדיוק ניגשים, בהינתן רשימה, לאיבר האמצעי בה?

בתכנות, שיטת אחסון נפוצה ופשוטה היא באמצעות מערך - איזור רציף בזכרון שמחולק ל”תאים”, כשכל תא מכיל פריט מידע. היתרון שבמערך הוא הגישה המהירה לכל איבר שבו - אם יודעים את כתובת תחילת המערך, את גודל כל תא במערך (הגודל של כל תא הוא אחיד) ואת מספר התא שאליו רוצים לפנות, אפשר לחשב את הכתובת המדוייקת בזכרון של התא, ולגשת אליו ישירות. דבר שכזה מכונה “גישה בזמן קבוע” - וכפי שנראה בהמשך, זה לא תמיד כך במבנים אחרים.

אם כן, אפשר לאחסן את המידע במערך, ואז לבצע את אלגוריתם החיפוש ביעילות. מה הבעיה במערך? שקשה להוסיף או להוריד ממנו איברים. אם אנחנו מסירים איבר, התוצאה תהיה תא ריק בתוך המערך - כלומר, זכרון מבוזבז (במסדי נתונים שיכולים להיות עצומים בתיאוריה אבל גם קטנטנים  זו בעיה מהותית), ואין שום דרך להוסיף איבר אם המערך הנוכחי מלא, כי ייתכן שהזכרון שמעבר לגבולות המערך כבר תפוס, ואם נקצה זכרון במקום אחר, נפגע בכך שהמערך רציף (ולכן גם בזמן הגישה המהיר לאיבריו). מכאן שצריך להחליט כבר בזמן הקצאת המערך כמה איברים הוא יוכל להכיל, מה שגורם לבזבוז הזכרון שכבר תיארתי ולכך שאם נצטרך להוסיף איבר למערך מלא, נהיה בבעייה. כמובן שקיימים פתרונות לבעיה זו - למשל, הקצאה של המערך מחדש בגודל כפול והעתקת המערך המקורי אליו - אבל יש גם גישה אחרת, שזונחת לגמרי את השימוש במערך - שימוש בעצים.

הרעיון בעצים (ובאח הקטן שלהם, רשימות מקושרות) הוא לשמור את המידע ב”תפזורת” בתוך הזכרון של המחשב - כל פריט מידע מאוחסן בשטח משלו, בלי הרציפות שמערך מבטיח. הרעיון הוא שכל פריט מידע “מצביע” על פריטי מידע אחרים - כלומר, זוכר את הכתובת שלהם. למשל, ברשימה מקושרת עם האיברים , A,B, כל מה שצריך לזכור הוא את כתובת A; ב-A עצמו יש את הכתובת של B וב-B את הכתובת של C, כך שאם רוצים להגיע ל-C צריך רק “לטייל” על הרשימה.

הבעיה כאן ברורה - זמן ההגעה לאיבר כלשהו של הרשימה תלוי באורך הרשימה, בעוד שבמערך הוא היה קבוע. העניין הוא שבמערך זמן הגישה היה קבוע רק אם ידענו במפורש לאיזה איבר אנחנו רוצים להגיע; לעתים קרובות היינו צריכים לחפש אותו גם במערך, וחיפוש בינארי היה דורש מאיתנו סיבוכיות זמן לוגריתמית. אם כן, האם ניתן לבנות מבנה נתונים “מקושר” כמו הרשימה המקושרת שבו גישה לאיבר כלשהו (שמזוהה על פי המפתח שלו) תדרוש זמן לוגריתמי? התשובה היא שאכן, הדבר אפשרי; והרעיון הוא בדיוק של שימוש בעץ חיפוש.

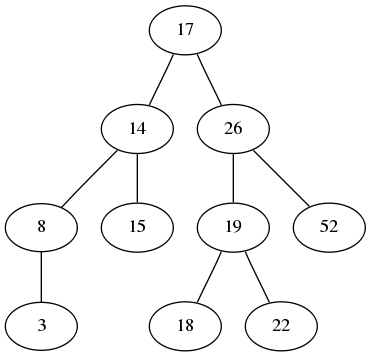
הרעיון בעץ חיפוש הוא פשוט - הבסיס של העץ, ומה שהמשתמש מחזיק מצביע אליו, הוא השורש. לשורש יש מספר בנים, שניתן למספר - הראשון, השני, השלישי וכו’ (בעץ בינארי, שבו יש לכל היותר שני בנים בכל צומת, מתייחסים אליהם כאל “הבן הימני” ו”הבן השמאלי”). כל אחד מהבנים הללו הוא בעצמו שורש של העץ שמתחיל ממנו והלאה - תת-עץ של העץ המקורי. הכלל המנחה בניית עצי חיפוש הוא זה: כל הצמתים בתת העץ של הבן הראשון קטנים יותר (בערך המספרי של המפתח שלהם) מכל הצמתים בתת העץ של הבן השני, וכן הלאה. המקרה הפשוט ביותר הוא של עץ בינארי, שבו הקריטריון הוא זה: בבן השמאלי יש את כל הצמתים שערך המפתח שלהם קטן מזה של השורש, ובבן הימני את כלו אלו שערך המפתח שלהם גדול יותר. הדוגמה שציירתי לעיל הייתה של עץ חיפוש בינארי שכזה.

אם כן, אלגוריתם חיפוש איבר בעץ חיפוש בינארי דומה מאוד לאלגוריתם החיפוש הבינארי שראינו - מתחילים מהשורש (“האיבר האמצעי” בחיפוש הבינארי) ומשווים את המפתח אליו. אם הם שווים - אחלה. אם המפתח של השורש גדול יותר, ממשיכים את החיפוש בתוך הבן השמאלי; אחרת, ממשיכים אותו בבן הימני. ממשיכים ככה עד שמוצאים את האיבר או “נתקעים” (כלומר, אין בן שמאלי/ימני למרות שצריך להיכנס אליו).

כל זה מאוד נחמד, אבל למרבה הצער, חסר ערך לחלוטין. הסיבה לכך היא שסיבוכיות אלגוריתם החיפוש במקרה הגרוע ביותר היא כעומק העץ (כלומר, כאורך המסלול הארוך ביותר מהשורש עד לאחד מהעלים), ועומק העץ עשוי להיות זהה (או קרוב מאוד) למספר הצמתים שבו - למשל, אם העץ הוא “שרוך” - ושרוך שכזה הוא פשוט רשימה מקושרת בתחפושת:

עם זאת, כל עוד שומרים על העץ מאוזן, כלומר שבתת העץ הימני של כל צומת יהיה בערך אותו מספר צמתים כמו בתת העץ השמאלי, העומק של העץ הוא לוגריתמי במספר הצמתים שבו, ולכן אלגוריתם החיפוש יהיה יעיל. על כן, עיקר העיסוק בעצי חיפוש הוא בעצים שמצליחים להישאר מאוזנים גם כאשר מכניסים ומוציאים מהם איברים, תוך הקטנת הזמן שפעולות אלו דורשות ככל הניתן. שתי דוגמאות לעצי חיפוש מאוזנים שכאלו הם עצי AVL ועצים אדומים-שחורים; בשניהם מאחסנים מידע נוסף בכל צומת שמקל על שימור האיזון של העץ.

דוגמת עצי החיפוש היא סטנדרטית ובסיסית; משתמשים בהם בכל מקום. עם זאת, אני חותר לדוגמה שלטעמי היא מעניינת עוד יותר, ובעלת יישומים מפתיעים יותר - עצי סיומות (Suffix trees) ושימושיהם בחיפוש מילים בטקסט ובכיווץ מידע.