מי שהיה נשוי שלוש נשים

הפעם אני רוצה לדבר על בעיה מתמטית חביבה שצצה במקום שנראה בלתי קשור בעליל - בתלמוד, במה שנראה לכאורה בתור דאגה לנשותיו של פוליגמיסט.

מקור החידה הוא במשנה במסכת כתובות (י’, ד’), שאומרת כך:

“מי שהיה נשוי שלש נשים ומת, כתובתה של זו מנה ושל זו מאתים ושל זו שלש מאות ואין שם (בעיזבונו) אלא מנה - חולקין בשוה; היו שם מאתים - של מנה נוטלת חמשים, של מאתים ושל שלש מאות שלשה שלשה של זהב; היו שם שלש מאות - של מנה נוטלת חמשים ושל מאתים מנה ושל שלש מאות ששה של זהב. וכן שלושה שהטילו לכיס (השקיעו בשותפות) - הותירו או פחתו, כך הן חולקין”

“מנה” כאן הוא 100, כך שהמשנה, בתרגום לעברית (כמו תרגום התנ"ך לעברית המתרגש ובא עלינו) הוא זה: אם יש לנו שלושה נושים, שהדרישות שלהם הם ל-100, 200 ו-300 ש”ח, ואין מספיק כסף כדי לשלם להם את מלוא הסכום, מבדילים בין שלושה מקרים אפשריים: אם יש רק 100 ש”ח, מחלקים את הסכום שווה בשווה בין כולם; אם יש 200, הרי שנותנים 50 לזה שדורש 100, ו-75 לשני האחרים; ואם יש 300, אז נותנים 50 לראשון, 100 לשני ו-150 לשלישי. במקרה הזה הנושים הן נשים, אבל כל העסק תקף באופן כללי למקרי פשיטת רגל שכאלו, שבהם צריך לחלק רכוש חלקי בין הנושים.

תמיד פשוט לסכם את הכלל המדובר בטבלה, אז הנה היא:

		הכתובה
		100	200	300
גודל העיזבון	100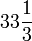
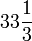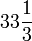	200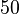
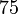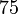	300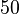

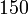(הטבלה מועתקת בזדון מויקיפדיה, אבל מותר לי כי אני כתבתי אותה במקור)

לכאורה מדובר בבעיה סגורה - נתנו לנו בדיוק את הכלל שלפיו יש לנהוג, וגמרנו. אלא שכמובן, אנחנו רוצים לדעת מה לעשות גם במקרים שבהם גודל העיזבון הוא לא 100, 200 או 300, אלא בכל מקרה אפשרי. לכן צריך להתבונן בטבלה ולהסיק את הכלל שלפיו היא נוצרה - דהיינו, כלל שיתאים לכל שלושת המקרים. כאן נוצרת לנו בעיה.

השורה הראשונה מציגה שיטת חלוקה שנשמעת הגיונית - שווה בשווה. זה בא למנוע מצב לא הוגן שבו בגלל שיש נושה שטוען לחוב עצום, הנושים האחרים יקבלו רק פרוטות - כלומר, זה הפתרון שמנסה להתחשב בכמה שיותר נושים. גם הפתרון השלישי נשמע הגיוני - חלוקה יחסית, כשכל נושה מקבל מהעיזבון סכום שחלקו מהעיזבון הכולל הוא כמו החלק של הנושה מהחוב הכולל (אם חצי מהחוב הוא שלך, תקבל חצי מהעיזבון). לעומת זאת, בשורה השנייה כלל לא ברור ההיגיון - למה דופקים את זה בעל החוב הקטן ביותר, בעוד ששני האחרים מתחלקים שווה בשווה? מה ההגיון כאן? האם יש הגיון?

ובכן, אין לי שמץ של מושג בתלמוד, אבל כששמעתי על העסק הזה בהרצאה של ישראל אומן, שאני מניח שמבין קצת יותר ממני (אם כי הוא הזהיר מראש שגם ההבנה שלו מוגבלת), הצלחתי להבין שלמרות שפרשני התלמוד ניסו להסביר את העניין הזה, הם לא ממש הצליחו, ובסופו של דבר דחו את השיטה המוזרה והעדיפו חלוקה שווה בשווה, וזהו.

קדימה למאה ה-20. אי שם בשליש הראשון של המאה ה-20 ממציא ג'ון פון-נוימן, מחשובי המתמטיקאים של המאה, את תורת המשחקים (בהתבסס, כמובן, גם על עבודות קודמות של מתמטיקאים אחרים). תורת המשחקים חוקרת בין היתר סיטואציות כאלו, של חלוקות; באופן כללי יותר היא מתעסקת במשחקים שבהם יש שיתוף פעולה בין קבוצות של שחקנים, ובשאלה איך “הוגן” לחלק את הרווחים שהקבוצות יפיקו משיתופי הפעולה הללו. שתי דוגמאות קלאסיות, שאותן יצא לי ללמוד (ורק אותן אני ממש מכיר) הן ה”ליבה” של המשחק, וערך שפלי (על שם המתמטיקאי לויד שפלי) שלו. אלו שתי דרכים שונות להגדיר את החלוקה ה”הוגנת” של הרווחים, ומכאן כבר ברור שאין דרך יחידה שהיא נכונה או מוצדקת; יש פשוט גישות שונות, שדורשות אקסיומות שונות. האקסיומות של ערך שפלי, למשל, נשמעות פשוטות וטבעיות - שכל הרווחים יתחלקו בין השחקנים, ששחקן שהוספתו לקבוצה לא תורמת רווח שהשחקן לא מרוויח ממילא לא יקבל יותר מאשר הרווח הזה, וכו’; ארבע האקסיומות שלו מספיקות כדי להבטיח שהוא תמיד יהיה קיים, ותמיד יהיה יחיד (“ערך” כאן הוא שם טיפה מבלבל; ערך שפלי הוא חלוקה לשחקנים של מה שכל השחקנים יכולים להשיג אם ישתפו פעולה). בין כל מושגי הפתרון השונים נמצא גם מושג בשם “גרעינון” (nucleolus), שבקרוב נחזור אליו.

הלאה, לשנות השמונים. ישראל אומן הוא כבר מתמטיקאי ותיק ומכובד, בעל רקורד מרשים בתורת המשחקים (שיזכה אותו יום אחד גם בפרס נובל). הוא יכול להרשות לעצמו “להשתעשע” (לא שאני רומז, חלילה, שחוקרים ללא רקורד לא יכולים או צריכים לעשות זאת). הוא ובנו שלמה (שנפל לאחר מכן במלחמת לבנון הראשונה) מנהלים דיון על מאמר של ברי א’וניל שעוסק בבעיות אחרות מהתלמוד שרלוונטיות לתורת המשחקים, ושלמה מספר לישראל על עניין מי שהיה נשוי לשלוש נשים. אומן מתלהב, מנסה לפתור את החידה יחד עם עמיתו מיכאל משלר (שנפטר לפני מספר חודשים), וביחד הם מגלים כי מושג הגרעינון המדובר מתאים בדיוק לפתרון שהתלמוד מציע. כאן אני צריך להתערב ולהסביר איך, בדיוק, אבל איני יודע; אני צריך לרענן את הידע שלי בתורת המשחקים (וללמוד את המושג הזה, שאיני מכיר) כדי לענות במדוייק על השאלה. אולי מישהו יסביר זאת בתגובות, ואולי אחזיר את החוב בפוסט מאוחר יותר.

ובכן, טוב ויפה. אבל מי שהמציא את המשנה הזו כנראה לא חשב על מושג הגרעינון, שמוגדר בצורה מתמטית פורמלית ואבסטרקטית למדי. השאלה היא, אם כן, האם ניתן לתאר את הכלל המנחה בעזרת מונחים שמתקשרים למשנה? שהגיוני שעליהם חשבו בעת המצאת המשנה? כעת, משאומן ומשלר ידעו מה הם בעצם מחפשים - מה הכלל המנחה במקרה הכללי - כנראה שהחיפוש הפך לקל יותר (או לפחות כך אומן אמר), והתשובה התגלתה בשיטת חלוקה תלמודית אחרת - “שניים אוחזין”.

גם לשניים אוחזין, שבמסכת בבא מציעא, יש ציטוט:

“שנים אוחזין בטלית… זה אומר: כולה שלי. וזה אומר: חציה שלי… זה נוטל שלשה חלקים, וזה נוטל רביע”

מדובר בשיטה מחוכמת למדי, לטעמי. אם ננסח את הסיטואציה של שניים אוחזין בעזרת הניסוח הכללי שלנו, יש לנו שני נושים, עיזבון של 100 ש”ח, והנושים דורשים 50 האחד, והשני דורש 100. אם כן, אין מספיק כסף כדי לחלק לשניהם את הכל. אפשר כמובן להפעיל את שתי שיטות החלוקה שאנו מכירים - חלוקה שווה בשווה תותיר את דורש ה-50 מאושר, עם כל החוב שהוא רצה לקבל; חלוקה “יחסית” תיתן 66.67 ש”ח לנושה של ה-100 ש”ח,ו-33.33 ש”ח לנושה של ה-50 ש”ח. כלומר, השיטה שמציעים בשניים אוחזין לא זהה לאף אחת משתי השיטות הללו. מתבקש לשאול “אם כן, מה השיטה הנכונה?” אבל שוב חשוב להזכיר שאין שיטה נכונה אחת, כל עוד לא החלטנו מה אנחנו רוצים לדרוש מהשיטה.

אם כן, מה ההגיון בשניים אוחזין לפיו זה שדורש 50 יקבל 25, וזה שדורש 100 יקבל 75? הרעיון הוא לבצע חלוקה שווה בשווה, אבל לא של כל הסכום; רק של החלק השנוי במחלוקת. הרי זה שדורש 50 בעצם אומר לנושה השניה “אני מסכים ש-50 ש”ח שייכים לך, אני רוצה רק את ה-50 הנותרים”. אם כן, ניתן 50 לנושה של ה-100; וכעת את ה-50 שנותרו נחלק שווה בשווה, כך שכל אחד יקבל עוד 25. הנושה של ה-50 יקבל 25, והנושה של ה-100 יקבל 75. שיטה מעניינת ונאה, לטעמי.

מה שאומן ומשלר שמו אליו לב הוא ששיטת “מי שהיה נשוי” היא בעצם הכללה של שניים אוחזין למקרה שבו יש יותר משני שחקנים. כמובן, המושג “הכללה” אינו מוגדר היטב ואפשר לחשוב על כמה דרכים שונות להכליל את השיטה הזו. המובן המדוייק של “הכללה” כאן הוא זה: אומן ומשלר קוראים לחלוקה (של עיזבון למספר כלשהו של נושים) “תואמת שניים אוחזין” אם היא מקיימת את התכונה הבאה - לכל זוג שחקנים, אם ניתן לכל שאר השחקנים את הסכום שהחלוקה נותנת להם ונחלק את מה שנשאר בין הזוג על פי “שניים אוחזין”, הרי שהחלוקה ששניים אוחזין תיתן תהיה זהה למה שהם אכן מקבלים בחלוקה המקורית.

מבלבל? בוודאי. לכן מסתכלים על דוגמאות. ניקח את המקרה שבו מחלקים 200 על פי הכלל המוזר שבטבלה. נניח שבעל החוב של ה-300 ש”ח התרצה, לקח את ה-75 ש”ח שלו ונעלם אל עבר השקיעה. נותרנו עם 125 ש”ח, ואז פתאום מתחילים שני בעלי החוב האחרים ללכת מכות. הם לא מוכנים לקבל את ההסדר המקורי - בפרט, זה שמקבל 50 מתאונן - ורוצים הסדר חדש. שניהם מסכימים ש”שניים אוחזין” זו השיטה הנכונה לחלק בה את הכסף. אם כן, אנחנו מחלקים ביניהם 125 ש”ח, כשאחד רוצה 100 והשני רוצה 200. כלומר, הסכום השנוי במחלוקת הוא 100, והנושה הראשון מוותר לשני מראש על 25 ש”ח; את ה-100 ש”ח השנויים במחלוקת הם מחלקים שווה בשווה. הנושה הראשון מקבל 50, והשני מקבל 75. הם מקבלים בדיוק את הסכום שבמקור רצינו לתת להם - כלומר, לא הייתה שום סיבה שהם יתחילו ללכת מכות, ופתאום החלוקה הלא הוגנת נראית קצת יותר הגיונית.

טיפלנו כאן רק בזוג שחקנים אחד - זה של ה-100 וזה של ה-200 נניח שדווקא זה של ה-100 התרצה, לקח את ה-50 שלו והלך. נותרו זה של ה-200 וזה של ה-300, ויש לנו רק 150 לחלק להם - כלומר, כל הסכום שנוי במחלוקת, ולכן הם חייבים לחלק אותו שווה בשווה. אם כן גם הזוג הזה “בסדר”, וקל לראות שגם הזוג השלישי “בסדר”, ושכל הטבלה גם כן בסדר ומקיימת את הכלל. לכן הכלל המקסים הזה, שהוא הכללה פשוטה של כלל שכבר קיים בתלמוד, נותן לנו קריטריון אחיד שמייצר את הטבלה כולה - ויותר מכך, ניתן להכללה לכל קבוצה של נושים וחובות.

כמובן, לא ברור אם מי שכתב את המשנה התכוון לפתרון הזה (שכזכור, מתאים גם לגרעינון, אבל בוודאי זה לא מה שעבר לכותב המשנה בראש); אבל חייבים להודות שזה משכנע למדי, וכנראה יהיה הדבר הקרוב ביותר לפתרון שהחידה הזו תזכה לו אי פעם (ניתן לראות את המאמר המקורי של אומן ומשלר, בקובץ PDF, כאן).

נותרנו רק עם בעיה אחת - הצלחנו להגדיר מתי חלוקה היא “תואמת שניים אוחזין”, אבל לא הראנו איך מוצאים אותה, או אם תמיד קיימת כזו. אומן ומשלר הוכיחו שהיא תמיד קיימת ויחידה והציעו אלגוריתם שמוצא אותה, אבל אני רוצה להציג כאן דווקא הוכחה מאוחרת יותר של מרק קמינסקי, שאומן הראה בהרצאתו, תוך מתן קרדיט מתאים לממציא. אני סבור שההוכחה פשוט יפהפיה, אחת ההוכחות המתמטיות המקסימות ביותר שנתקלתי בהן מעודי. במקום לנסות לנמק מדוע, הנה הרעיון הבסיסי: חוק הכלים השלובים.

חוק הכלים השלובים הוא חוק פיזיקלי, שמתבסס על הרעיון המתמטי יחסית של “שאיפה למינימום אנרגיה” של מערכות בטבע (כי ככל שיש במערכת פחות אנרגיה, כך היא יותר יציבה. בערך). הוא עוסק במצב שבו יש לנו מספר כלים המכילים נוזל, ומחוברים זה לזה באופן שמאפשר לנוזל לנוע בחופשיות. במצב שכזה, גובה פני המים בכל הכלים יהיה שווה (לא במדוייק, כמובן; כמו כל דבר בטבע, מה שיקרה הוא רק שנראה שהנוזל “שואף” למצב הזה). הנה תמונה שממחישה מה קורה במציאות:

מה לחוק פיזיקלי ולמתמטיקה? ישירות, כלום; בפועל, החוק משמש כאמצעי לשיפור ההבנה של ההוכחה. הרעיון הבסיסי הוא לייצג את החוב של כל נושה בתור כלי שנפחו הוא בדיוק כגודל החוב ובנוי בצורה מחוכמת שתכף אסביר, לייצג את העיזבון בתור נוזל, לחבר את הכלים של כל הנושים יחדיו, לשפוך את הנוזל לתוך הכלים ולתת לחוק הכלים השלובים לעשות את שלו - אחרי שיישפך כל הנוזל, אפשר יהיה לנתק את כל הכלים זה מזה, וכמות הנוזל שבכל כלי תהיה בדיוק כמות הכסף שמגיעה לאותו בעל חוב.

הנה המחשה של העניין, שוב מויקיפדיה העברית (ושוב, אני מרשה לעצמי כי אני יצרתי את התמונות הללו):

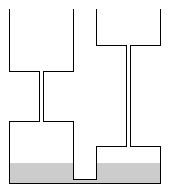
בתמונה הזו יש לנו שני נושים, ואפשר לראות את המבנה המוזר של הכלים שלהם. כל כלי מורכב משני חלקים בעלי נפח זהה, בצורה כזו ששני החלקים התחתונים מתחילים מאותו גובה, ושני החלקים העליונים מסתיימים באותו גובה. מקפידים על כך שהרוחב של כל כלי יהיה זהה, כך שההבדלים היחידים הם באורכים של שני חלקי כל כלי. בין החלק התחתון לעליון בכל כלי מחברת צינורית דקה שמאפשר מעבר נוזל אבל כמות הנוזל שנמצאת בתוכה היא אפסית.

אם כן, החלק התחתון של כל כלי מסמל מחצית מן הדרישה של בעל החוב, והחלק העליון מסמל את החצי השני. כעת, אם העסק באמת עובד כפי שהוא אמור לעבוד, הרי שכשנשפוך פנימה חוב, נקבל חלוקה שהיא בדיוק על פי “שניים אוחזין”. האמנם?

אומן מפריד בין שלושה מקרים. ראשית, ייתכן שיש מעט מדי נוזל ואפילו החלק התחתון של שני הכלים לא יתמלא. במקרה הזה מה שקיבלנו הוא חלוקה שווה בשווה של החוב. האם זה גם מה שהיה צריך להתקיים? כן, בתנאי שכמות הנוזל הכוללת (בשני הכלים גם יחד) אינה עולה על קיבולת הכלי הקטן יותר - במילים אחרות, גודל העיזבון כולו אינו גדול אפילו מהדרישה של הנושה הראשון, ולכן כל הסכום שנוי במחלוקת. די ברור שזו אכן הסיטואציה כאן, כי כמות הנוזל הכוללת בשני הכלים תהיה שווה לדרישה של הנושה הראשון בדיוק ברגע שבו כמות הנוזל בכלי שלו תהיה שווה לחצי מהדרישה שלו - כלומר, כשרק החלק התחתון של הכלי יתמלא.

ומה קורה כשמוזים נוזל כך שהחלק התחתון של אחד הכלים מתמלא? כאן יש לנו שתי אפשרויות - או שגם החלק התחתון של הכלי השני יתמלא, או שלא. הנה שתי האפשרויות:

בכל אחד משני המקרים הללו קורה אותו הדבר בדיוק - בעל הכלי הגדול יותר מקבל את כל הנוזל הנוסף. האם זה גם מה שהיה צריך לקרות? כן, כי “חלוקה שווה של הסכום השנוי במחלוקת” כבר בוצעה בדיוק עד שהתמלא חלקו הראשון של הכלי הקטן יותר; מכאן והלאה שאר הנוזל אינו שנוי במחלוקת, ולכן מגיע לבעל הכלי הגדול יותר.

ומה המקרה השלישי? המקרה שבו פני הנוזל עולים כל כך הרבה שגם חלקו העליון של הכלי הקטן יותר מתחיל להתמלא:

זה קצת מבלבל. מה זה בא לתאר? למה שגם בעל הכלי הקטן יקבל כסף? הרי חשבנו שכבר טיפלנו בכל הסכום השנוי במחלוקת!

בואו נחשוב לרגע מה קורה כשגובה הנוזל הוא כזה שהחלק העליון בכלי הקטן טרם התחיל להתמלא, אבל עוד טיפה ויתמלא. הכלי האחר מלא כמעט לגמרי; מה טרם התמלא בו? רק החלק העליון ביותר, ששווה בנפחו בדיוק לחלק העליון בכלי הקטן. אם כן, מהי כמות הנוזל הכללית שנשפכה עד עתה? בדיוק מה שיש בכלי הגדול ועוד מה שיש בכלי הקטן, בחלקו התחתון; אבל מה שיש בחלקו התחתון שווה בנפחו לחלקו העליון, כלומר למה שעוד נשאר לכלי הגדול עד שיתמלא לגמרי. בקיצור (ולא חשוב אם לא הבנתם את הנימוק) - אנחנו מגיעים לסיטואציה השלישית כאשר העיזבון גדול משתי הדרישות של הנושים. זו סיטואציה חדשה עבורנו; עד כה חשבנו על מקרים שבהם אחד הנושים אמר על הטלית “כולה שלי”, והנה סיטואציה שבה שני הנושים מסכימים שיש חלק בטלית ש”לא מגיע להם”. מצד שני, עדיין אין מספיק נוזל כדי למלא את הכלים של שניהם גם יחד, ולכן כל הנוזל צריך להתחלק איכשהו ביניהם - אבל איך?

הרעיון הוא שכל אחד יוותר לשני קצת. נניח שיש לנו שני בעלי חוב, אחד של 100 ש”ח והשני של 150 ש”ח, ושיש 200 ש”ח לחלק לשניהם. אז הראשון מוותר לשני על 100 ש”ח, והשני מוותר לראשון על 50 ש”ח; המריבה נותרת רק על 50 השקלים הנותרים, שיתחלקו שווה בשווה. כרגיל, תמונה אחת מסבירה הכי טוב:

הקו האדום מייצג את ה-100 ש”ח של נושה מס’ 1, והכחול את ה-150 ש”ח של נושה מס’ 2; החלק האמצעי הוא זה של הסכום השנוי במחלוקת. החלק השנוי במחלוקת מתחלק שווה בשווה, ולכן ההפרש בין הסכום שנושה מס’ 2 יקבל והסכום שנושה מס’ 1 יקבל הוא בדיוק ההפרש בין הסכום שעליו נושה מס’ 1 ויתר, והסכום שעליו נושה מס’ 2 ויתר. נסו להבהיר לעצמכם למה (ומה לעזאזל אמרתי כאן) - זה דורש חישוב קצר.

אומן ניסח את התכונה הזו יותר באלגנטיות: “ההפרש בין הכתובות הוא ההפרש בין המנות”, או בתרגום לשפת הנושים והחובות - ההפרש בין החובות יהיה גם ההפרש בין הכסף שכל אחד יקבל. זה הכלל שמנחה את החלוקה במקרה הזה, ואם נחזור לכלים השלובים, נראה שזו בדיוק התכונה שהם מקיימים. ברור לנו שבכלי הגדול יש יותר נוזל מאשר בכלי הקטן, אבל כמה יותר? בדיוק כנפח החלק של הכלי הגדול שהוא רחב בזמן שבכלי הקטן יש באותו גובה רק את הצינורית הדקיקה. כל החלק הזה שווה בגודלו להפרש שבין הנפחים של הכלים - כלומר, של החובות - ומכיוון שכמות הנוזל שהם קיבלו בשאר חלקי הכלים שלהם זהה, זה יהיה גם ההפרש בין המנות שהם יקבלו.

אם כן, הכלים השלובים מקיימים את “שניים אוחזין” לכל זוג כלים נפרד, אבל איך זה מוביל למקרה הכללי? כאן מגיע החלק היפה ביותר - זה מגיע באופן מיידי. הנה דוגמה לסיטואציה שבה יש ארבעה בעלי חוב:

הנוזל נשפך לכלים והתאזן על פי שניים אוחזין; כעת, מדוע החלוקה הזו היא תואמת שניים אוחזין? כי אם ננתק את כל הכלים פרט לשניים, גובה פני הנוזל לא ישתנה - וכבר ראינו שעבור כל זוג, אכן מתקיימת תכונת שניים אוחזין. זהו, זה הכל.

אם כן, אלגוריתם שמחשב את החלוקה פשוט יבצע סימולציה של שפיכת הנוזל לכלים. מכיוון ששפיכת הנוזל היא תהליך רציף, ואילו המחשב מבצע חישובים בדידים, האלגוריתם יתקדם בקפיצות; קודם הוא יקפוץ מהמצב שבו כל הכלים ריקים למצב שבו נשפך לכלים נוזל כך שחלקו התחתון של הכלי הקטן ביותר התמלא - עד אז, כולם קיבלו בדיוק אותה כמות. כעת הוא ימשיך לחלק את הכמות שנותרה מהעיזבון בין כל השחקנים פרט לזה עם הכלי הקטן ביותר, עד שעוד חלק תחתון יתמלא, וכן הלאה וכן הלאה. אחרי שכל הכלים התחתונים יתמלאו, הרי שהעיזבון הוא לפחות כגודל חצי מהדרישות; לכן במקרה כזה אפשר פשוט “להתחיל מהסוף” - בסיטואציה שבה כל הכלים מלאים, ודווקא גורעים מהם נוזל עד שסכום הנוזל בכל הכלים שווה לעיזבון.

האם אכן זה מה שהתלמוד התכוון אליו? האם מלמדים את השיטה הזו כיום בלימודי התלמוד? אני משאיר את העיסוק בשאלות הללו לתגובות.