מספרים קונגרואנטים, ואיך זה קשור לעקומים אליפטיים

עקומים אליפטיים זכו לחשיפה רחבה יחסית בעשורים האחרונים, במיוחד בשל הקשר שלהם להוכחת המשפט האחרון של פרמה, והקשר שלהם לקריפטוגרפיה. לטעמי אכן מדובר בתחום מעניין ביותר, אף כי איני מבין בו כמעט שום דבר. למרות זאת אנסה לתאר (כאן ובפוסטים עתידיים) מקצת מהתיאוריה שלהם; בתקווה, אוכל אפילו לתאר באופן כללי ביותר את הרעיון שמאחורי הוכחת המשפט האחרון של פרמה.

אתחיל מבעיה “קלאסית” בתורת המספרים שהפתרון אליה - שהוא מודרני מאוד, משנות השמונים של המאה ה-20 - עובר דרך עקומים אליפטיים - בעיית המספרים הקונגרואנטיים. שורשיה של הבעיה נמצאים כבר אצל היוונים הקדמונים, אך ניסוח מפורש שלה יש רק אצל המתמטיקאים הערביים בני המאה ה-10. השאלה עוסקת במשולשים ישרי זווית, כלומר משולשים שצלעותיהן מקיימות את משפט פיתגורס המפורסם: \( a^{2}+b^{2}=c^{2} \). כזכור, היוונים לא אהבו מספרים אי רציונליים, ולכן התעניינו במשולשים ישרי זווית שכל צלעותיהם רציונליות, והשאלה היא מהם השטחים האפשריים למשולשים שכאלו. בפרט, מהם השטחים שהם מספר שלם. אם יש לנו משולש ישר זווית עם שוקיים \( a,b \) אז שטחו הוא \( \frac{ab}{2} \). לכן אפשר לנסח את הבעיה כבעיה בתורת המספרים: אילו מספרים טבעיים \( n\in\mathbb{N} \) מקיימים \( n=\frac{ab}{2} \) עבור \( a,b \) רציונליים, שבנוסף לכך גם מקיימים ש-\( \sqrt{a^{2}+b^{2}} \) רציונלי? מספרים כאלו נקראים (מסיבה שאינה ברורה לי והיא כנראה היסטורית) “מספרים קונגרואנטים”.

ובכן, קל מאוד לייצר משולשים ישרי זווית שכל צלעותיהם הם מספרים שלמים: אלו הן השלשות הפיתגוריות. אזכיר בחטף שאפשר לייצר שלשות פיתגוריות באופן סדרתי: לוקחים \( x,y \) הזרים זה לזה ואחד מהם לפחות הוא זוגי, ואז מגדירים \( a=x^{2}-y^{2},b=2xy,c=x^{2}+y^{2} \) והופס - קיבלנו שלשה פיתגורית. מכיוון ש-\( b \) הוא זוגי, אז \( \frac{ab}{2}=xy\left(x^{2}-y^{2}\right) \) הוא שלם. לכן קיבלנו דרך פשוטה לייצר המוני מספרים קונגרואנטים. לכן הבעיה איננה עם ייצור של מספרים שכאלו, אלא עם בדיקה, בהינתן מספר טבעי כלשהו, האם הוא קונגרואנטי או לא. כלומר, האם קיים משולש ישר זווית עם צלעות רציונליות ששטחו שווה למספר זה.

למשל, עבור השלשה הפיתגורית \( a=3,b=4,c=5 \) נקבל שטח של \( 6 \), ולכן \( 6 \) הוא מספר קונגרואנטי. מה עם מספרים קטנים יותר, למשל 5? ובכן, מסתבר ש-5 הוא כן מספר קונגרואנטי, אבל בבירור המשולש ששטחו הוא 5 אינו יכול להיות בעל צלעות שהן מספרים טבעיים; כי אם \( 5=\frac{ab}{2} \) אז \( ab=10 \), אבל אז \( a=5,b=2 \) או ש-\( a=1,b=10 \), ובשני המקרים הללו נקבל \( c \) שאינו שלם (ובעצם אינו רציונלי). אז מדוע 5 הוא כן קונגרואנטי? כי אם נתבונן על המשולש שצלעותיו הן \( 1\frac{1}{2},6\frac{2}{3},6\frac{5}{6} \), על ידי חישוב זריז אפשר לראות שזהו אכן משולש “חוקי”(משפט פיתגורס מתקיים) וששטחו הוא 5. אם כן, זה לא מקרי שאנחנו מדברים על צלעות רציונליות ולא על צלעות שלמות; אם מרשים צלעות רציונליות, יותר מספרים שלמים יכולים להתקבל בתור שטח.

ייתכן שאתם תוהים כעת מדוע להגביל את עצמנו ולדרוש שהשטח יהיה שלם ולא לדבר על שטח רציונלי - כלומר, לשאול את השאלה אילו מספרים רציונליים יכול להתקבל כשטח של משולש ישר זווית עם צלעות רציונליות. הסיבה פשוטה: אם \( a,b,c \) הן צלעותיו של משולש כזה ו-\( s \) הוא מספר רציונלי כלשהו, אז גם \( sa,sb,sc \) הן צלעותיו של משולש ישר זווית עם צלעות רציונליות. שטחו של המשולש הזה יהיה \( \frac{\left(sa\right)\left(sb\right)}{2}=s^{2}\frac{ab}{2} \), כלומר כפל של שטח המשולש המקורי בריבוע. לא קשה להראות שבאמצעות כפל כזה בריבוע, מכל מספר רציונלי אפשר לקבל מספר שלם שאיננו מתחלק על ידי ריבוע של מספר שלם (מספר שכזה נקרא “חופשי מריבועים”). למשל, הבה ונתבונן במשולש שצלעותיו הן \( \frac{3}{2},\frac{4}{2},\frac{5}{2} \); שטחו הוא \( \frac{3}{2} \). על ידי כפל ב-\( 2^{2} \) נקבל 6 - בדיוק השטח של המשולש \( a=3,b=4,c=5 \) שעליו דיברנו כבר. למעשה המשולש \( \left(\frac{3}{2},\frac{4}{2},\frac{5}{2}\right) \) אינו שונה מהותית מהמשולש \( \left(3,4,5\right) \); הזוויות שבתוכו זהות - הוא דומה למשולש \( \left(\frac{3}{2},\frac{4}{2},\frac{5}{2}\right) \). פרט לגודל, הם נראים אותו דבר בדיוק (ולכן \( \left(\frac{3}{2},\frac{4}{2},\frac{5}{2}\right) \) נראה כאילו אנחנו מסתכלים על \( \left(3,4,5\right) \) “יותר מרחוק”). פורמלית, אפשר להגדיר מחלקות שקילות על מספרים רציונליים, כך ששני מספרים הם שקולים אם ורק אם אפשר לקבל אחד מהשני על ידי כפל בריבוע; מה שאמרתי קודם ניתן לניסוח פורמלי כטענה שלכל מחלקת שקילות ניתן לבחור נציג שהוא מספר שלם חופשי מריבועים, וכדי לעסוק בשאלת המספרים הקונגרואנטים, אם כן, די לטפל בנציגים. לאחר מכן, אם יהיה לנו מספר רציונלי \( r \) כלשהו ונרצה לדעת אם הוא שטח של משולש ישר זווית רציונלי או לא, פשוט נכפול אותו ב-\( s^{2} \) מתאים, נקבל מספר טבעי חופשי מריבועים, ונפתור את הבעיה עבורו.

עכשיו משהבנו מהם מספרים קונגרואנטים, אציג הגדרה שונה ושקולה עבורם: \( n \) הוא קונגרואנטי אם ורק אם קיים \( x \) רציונלי שהוא ריבוע של מספר רציונלי, כך ש-\( x+n,x-n \) שניהם ריבועים של מספרים רציונליים. הגדרה זו, ולא הניסוח המקורי, היה מה שעניין את הערבים.

במבט ראשון לא ברור מה הקשר בין שתי הבעיות, ולכן אתאר בקצרה את הרעיון: אם \( \left(a,b,c\right) \) הוא משולש ישר זווית רציונלי כך ש-\( n=\frac{ab}{2} \), אז נגדיר \( x=\left(\frac{c}{2}\right)^{2} \). במילים אחרות, \( x=\frac{a^{2}+b^{2}}{4} \), ועל כן \( x+n=\frac{a^{2}+2ab+b^{2}}{4}=\left(\frac{a+b}{2}\right)^{2} \), ובדומה \( x-n=\left(\frac{a-b}{2}\right)^{2} \), כך שבמקרה זה \( x+n \) ו-\( x-n \) הם אכן ריבועים של מספרים רציונליים. בכיוון ההפוך, אם יש לנו \( x \) שמקיים את התכונה הנ”ל, אז אפשר לבנות ממנו משולש מתאים עם \( a=\sqrt{x+n}-\sqrt{x-n},b=\sqrt{x+n}+\sqrt{x-n},c=2\sqrt{x} \) (שימו לב כיצד אנו משתמשים כאן בכך ש-\( x,x+n,x-n \) הם כולם ריבועים של משהו רציונלי).

צורת ההצגה הזו מאפשרת לנו לראות בקלות יחסית עד כמה השאלה “האם המספר \( n \) הוא קונגרואנטי?” יכולה להיות בעייתית גם במקרים של ערכים ספציפיים של \( n \): בפרט, עבור \( n=1 \) השאלה היא האם קיים \( x \) כך ש-\( x,x+1,x-1 \) כולם ריבועים של מספרים רציונליים. מכיוון ש-\( x+1 \) ריבוע ו-\( x-1 \) ריבוע, אז \( \left(x+1\right)\left(x-1\right) \) הוא חזקה רביעית של מספר רציונלי שנסמנה \( a^{4} \). בדומה, גם \( x^{2} \) הוא חזקה רביעית של מספר רציונלי שנסמנו \( c^{4} \). אז בעצם ראינו ש-\( a^{4}=\left(x+1\right)\left(x-1\right)=x^{2}-1=c^{4}+1 \), ובמילים אחרות - \( a^{4}+1^{4}=c^{4} \) והופס, על ידי כפל במכנה המשותף של \( a,c \) - קיבלנו הפרכה למשפט האחרון של פרמה עבור חזקה רביעית. זה מבהיר לנו מייד כי \( n=1 \) אינו מספר קונגרואנטי, כי אנחנו יודעים שהמשפט האחרון של פרמה נכון (מדוע זה לא עובד עבור כל \( n \)? כי הסתמכנו על כך ש-\( n^2=m^4 \) עבור \( m \) שלם כלשהו, מה שבלתי אפשרי עבור \( n \) חופשי מריבועים הגדול מ-1).

אם כן, הבעיה של בדיקה האם מספר הוא קונגרואנטי איננה טריוויאלית. מה שאנחנו רוצים למצוא הוא דרך פשוטה כלשהי לאפיין את המספרים הקונגרואנטיים. במילים אחרות, למצוא אלגוריתם שמקבל מספר \( n \) ואומר אם הוא קונגרואנטי או לא. ברור שאפשר פשוט לעבור סדרתית על כל המשולשים עם צלעות רציונליות שקיימים (כי אוסף כל השלשות של מספרים רציונליים הוא בן מניה ולכן אפשר לעבור סדרתית על איבריו) אבל זה מבטיח לנו רק שנעצור ונגיד “כן” על מספרים שהם כן קונגרואנטיים; זה לא אומר לנו מתי נוכל לעצור אם מספר איננו קונגרואנטי. זהו לב הבעיה - בעיה שנותרה פתוחה אלפי שנים.

בשנות השמונים פרסם Tunnel פתרון כמעט מלא לבעיה. “כמעט מלא” במובן זה שאחד הכיוונים בו לא הוכח לחלוטין, אלא התבסס על נכונות השערה מפורסמת מאוד בתורת המספרים - השערת בירץ' וסווינרטון-דייר. למעשה, המשפט של טאנל לא נזקק למלוא הכוח של ההשערה אלא רק למקרה פרטי מאוד שלה, ומאז כבר הוכיחו מקרה פרטי של המקרה הפרטי הזה - אך למיטב ידיעתי, טרם הוכיחו את המקרה הפרטי המדובר במלואו, כך שהבעיה עוד לא נפתרה סופית, אך כל הסימנים מעידים על כך שזמנה קרב, בדומה לאופן שבו העידו הסימנים על כך שזמנה של בעיית המשפט האחרון של פרמה קרב. נראה לי שהכי פשוט יהיה להציג את הקריטריון שנתן טאנל ורק לאחר מכן להתחיל לדון עליו.

נניח לרגע ש-\( n \) אי זוגי וחופשי מריבועים. אז על פי טאנל, \( n \) הוא קונגרואנטי אם ורק אם מספר הפתרונות בשלמים של המשוואה \( n=2x^{2}+y^{2}+32z^{2} \) הוא כפול ממספר הפתרונות בשלמים של המשוואה \( n=2x^{2}+y^{2}+8z^{2} \). עבור \( n \) זוגי יש צמד משוואות דומות. זהו. שימו לב שמכיוון שמדובר על פתרונות בשלמים למשוואה הזו, וכל המשתנים הם בריבוע, יש רק מספר סופי של הצבות שיש לבצע כדי לספור את מספר הפתרונות של המשוואה, והוא אפילו לא גדול מהותית ביחס ל-\( n \), כלומר הפתרון הוא אפילו יעיל יחסית (“יחסית”, כי בדרך כלל כשמדובר על אלגוריתמים במספרים נדרשת יעילות ביחס לגודל הייצוג של המספר ולא ביחס לגודל שלו עצמו - אבל נעזוב את זה).

אם כן, השאלה המקורית היא פשוטה למדי מבחינת הניסוח שלה. גם הקריטריון הסופי הוא פשוט למדי מבחינת הניסוח שלו. מה שקורה באמצע, לעומת זאת, לחלוטין לא פשוט; המתמטיקה שמובילה מבעיית המספרים הקונגרואנטים אל הפתרון שלה עוברת דרך המתמטיקה המודרנית של המאה ה-20, עמוק אל תוך השטח שפתר גם את המשפט האחרון של פרמה - עקומים אליפטיים ותבניות מודולריות. הייתי שמח לומר שאני מסוגל להסביר את הפתרון בשלמותו, אבל לפחות כרגע אני מאוד, מאוד לא בקיא בפרטיו, ויכול להסביר רק את הרעיון הכללי. נתחיל מהאופן שבו עקומים אליפטיים נכנסים בכלל לסיפור.

כאמור, אם \( n \) קונגרואנטי אז קיים \( x \) רציונלי כך ש-\( x,x+n,x-n \) הם ריבועים כולם. לכן גם מכפלתם היא ריבוע, שנסמנו \( y^{2} \), ומכפלה זו שווה ל- \( x\left(x+n\right)\left(x-n\right)=x\left(x^{2}-n^{2}\right)=x^{3}-n^{2}x \). בקיצור, אם \( n \) קונגרואנטי אז קיים זוג \( \left(x,y\right) \) של נקודות רציונליות כך ש-\( y^{2}=x^{3}-n^{2}x \). המשוואה הזו היא דוגמה קלאסית לעקום אליפטי.

קצת קשה לתת את ההגדרה המדוייקת לעקום אליפטי בלי להשתמש במושגים מתקדמים למדי; ההגדרה של ויקיפדיה העברית לעקום אליפטי מעל שדה \( K \) היא “עקום אלגברי פרויקטיבי, לא סינגולרי, מעל \( K \) מגנוס 1, עם נקודה קבועה המוגדרת מעל \( K \)”. עקום אלגברי הוא מקרה פרטי של יריעה אלגברית, שם שאולי נשמע מפחיד אבל אינו כל כך נורא בשורה התחתונה: יריעה אלגברית היא פשוט אוסף כל הנקודות שמאפסות פולינום מסויים במספר משתנים (או, כמו שקורה לרוב, אוסף של פולינומים שכאלו) מעל שדה נתון. כך למשל הפולינום עבור העקום האליפטי שלנו הוא \( f\left(x,y\right)=y^{2}-x^{3}+n^{2}x \). התחום העוסק ביריעות אלגבריות נקרא גאומטריה אלגברית; זהו תחום מתקדם ומודרני למדי במתמטיקה, ואין לי שום סיכוי להציג אותו בצורה ראויה בשלב זה. לכן אסתפק בתיאור עקומים אליפטיים בשיטת “Bottom-up’’ - אגדיר אותם בצורה צרה יחסית, שמפספסת את התיאוריה הכללית שמסביב, וכאילו שלא די בכך - גם אתעלם ממקרי קצה על ימין ועל שמאל.

אם כן, לצורך שלנו, עקום אליפטי הוא פשוט אוסף הנקודות שמאפסות משוואה מהצורה \( y^{2}=p\left(x\right) \), כש-\( p \) הוא פולינום ממעלה שלישית, מעל שדה \( \mathbb{F} \) כלשהו. הן המשוואה שמגדירה את העקום והן השדה שממנו נלקחים הפתרונות משנים באופן מהותי את המבנה שלו ולכן נהוג בדרך כלל לתאר את שניהם גם יחד: למשל \( E/\mathbb{F} \) או \( E\left(\mathbb{F}\right) \) הן צורות סימון מקובלות. על \( p\left(x\right) \) דורשים דרישה נוספת - שכל שלושת שורשיו יהיו שונים (אין ל-\( p \) בהכרח שורשים ב-\( \mathbb{F} \), אך תמיד יש לו שורשים בהרחבה סופית כלשהי של \( \mathbb{F} \)) - דרישה זו מבטיחה שהעקום יהיה “חלק” - לא אסביר כרגע מה זה אומר או למה זה אומר את זה או למה צריך את זה.

אם המציין של \( \mathbb{F} \) שונה מ-2 או 3, כלומר אם המשוואות \( 1+1=0 \) ו-\( 1+1+1=0 \) אינן נכונות ב-\( \mathbb{F} \) (בשדה \( \mathbb{Z}_{2} \) המשוואה \( 1+1=0 \) דווקא כן נכונה, למשל) אז אפשר על ידי התחכמויות אלגבריות לכתוב כל עקום אליפטי בעזרת המשוואה הבאה: \( y^{2}=x^{3}+ax+b \). העקום מאופיין, אם כן, על ידי הפרמטרים \( a,b \). בעקום שדיברנו עליו למעלה \( a=-n^{2} \) ו-\( b=0 \).

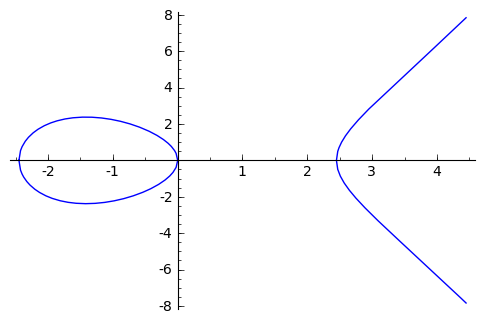
הנה איך כל זה נראה מעל \( \mathbb{R} \):

התמונה קצת מבלבלת כי יש עקומים שלא נראים כך, ומורכבים רק מחתיכה אחת, אבל זה נותן את הרעיון הכללי. כמו שאפשר לראות מהתמונה, עקומים אליפטיים לא מזכירים בכלל אליפסות. אז למה “אליפטיים”? מסיבות היסטוריות (קשר לאינטגרלים אליפטיים, שנקראים כך כי הם צצו לראשונה בהקשר של חישוב אורך קשת של אליפסה) שלא אציג כרגע.

בנוסף לכל הצרות, לכל עקום אליפטי יש נקודה נוספת, לא מתוך \( \mathbb{F} \), שנמצאת “באינסוף”. הדרך הפורמלית והמדוייקת לתאר אותה היא להסתכל על מרחב פרוייקטיבי מעל \( \mathbb{F} \) (ושם נקודת ה”אינסוף” מתקבלת בתור פתרון חוקי לגמרי למשוואה שמגדירה את העקום) אבל גם זה נושא לפוסט בפני עצמו ולכן לעת עתה נסתפק בהבנה שקיימת כזו נקודה ושהיא חוקית לגמרי מבחינה מתמטית. את הנקודה הזו מסמנים בדרך כלל ב-\( \mathcal{O} \), מסיבה שתכף תתברר.

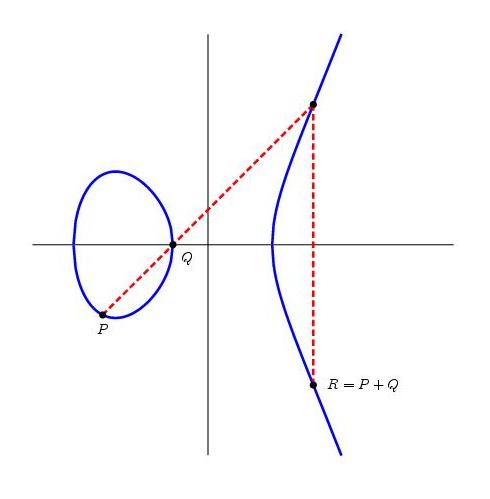
כעת הפאנץ’ - כל עקום אליפטי מהווה חבורה אבלית, ביחס לפעולת “חיבור”משונה למדי (משונה, במבט ראשון). מכיוון שהתגובה הראשונית לתיאור הפעולה הזו היא משעשעת למדי, אתאר אותה כאן בזריזות - הסבר אמיתי יגיע בפוסט נפרד. באופן כללי, הרעיון הוא כזה: כדי לחבר שתי נקודות \( P,Q \) על העקום, יש להעביר את הישר שעובר דרך שתיהן. אם הוא לא חתך שוב את העקום, אז סכום הנקודות יהיה \( \mathcal{O} \); אבל אם הוא כן חתך אותו שוב… ובכן, מתבקש להגדיר את נקודות החיתוך בתור \( P+Q \), נכון? אבל במקום זה, לוקחים את השיקוף ביחס לציר \( x \) של נקודת החיתוך בתור \( P+Q \). מה, לא ברור?

הנקודה באינסוף \( \mathcal{O} \) משמשת בתור היחידה ביחס לחיבור, כלומר \( P+\mathcal{O}=P \) לכל \( P \). ההופכי של כל נקודה \( P \) הוא פשוט השיקוף שלה ביחס לציר \( x \), ולכן אפשר לתאר את כלל החיבור גם באופן הבא: אם \( P,Q,R \) הן שלוש נקודות של העקום שנמצאות על אותו ישר, אז \( P+Q+R=\mathcal{O} \) (למה זה באמת שקול למה שתיארתי קודם?). לבסוף צריך להבהיר איך מחברים נקודה עם עצמה - אם רוצים לחשב את \( P+P \) הרי לא ניתן להעביר ישר “דרך \( P \) וגם דרך \( P \)“כי ישנם אינסוף ישרים שכאלו. מה שכן עושים הוא לקחת את הישר שמשיק לעקום האליפטי בנקודה \( P \) (כאן נכנסת לתמונה העובדה שהעקום הוא חלק, ולכן ניתן להעביר לו משיק שכזה), ומכאן ממשיכים כרגיל - מוצאים את נקודת החיתוך הנוספת עם העקום (אם אין כזו, \( P+P=\mathcal{O} \)) ולוקחים את השיקוף שלה.

כל זה נשמע מאוד מוזר, כל עוד לא רואים מהיכן הפעולה הזו מגיעה. לעת עתה תצטרכו לסמוך עלי שיש הסבר הגיוני ואפילו יפה לכל זה, ושארחיב עליו בעתיד; לעת עתה אני רוצה להסביר איך כל זה מתקשר לעניין המספרים הקונגרואנטיים.

ובכן, מה שראינו עד כה היה שאם \( n \) הוא מספר קונגרואנטי, אז קיימת נקודה \( \left(x,y\right) \) עם קוארדינטות רציונליות כך ש-\( y^{2}=x^{3}-n^{2}x \). במילים אחרות, קיימת נקודה על העקום האליפטי \( y^{2}=x^{3}-n^{2}x \) מעל השדה \( \mathbb{Q} \) - אסמן אותו כ-\( E_{n}\left(\mathbb{Q}\right) \). ניתוח יותר זהיר של הסיטואציה מראה שלא כל נקודה על העקום מתקבלת באופן הזה, ושגם אם יש נקודה על העקום, זה עדיין לא מבטיח ש-\( n \) קונגרואנטי. אז איך כל זה עוזר לנו? כי באמצעות הניתוח הזהיר (שלא אציג כרגע) אפשר להראות ש-\( n \) הוא קונגרואנטי אם ורק אם \( E_{n}\left(\mathbb{Q}\right) \) מכיל אינסוף נקודות. בכך הפכה בעיית המספרים הקונגרואנטיים לבעיה על עקומים אליפטיים. רק אעיר שה”ניתוח הזהיר” מתבסס בצורה חזקה מאוד על ניתוח הפעולה שמוגדרת על נקודות העקום - בפרט, הוא מראה שנקודה שמוכיחה ש-\( n \) קונגרואנטי חייבת להיות בעלת התכונה שכשאשר מחברים אותה לעצמה שוב ושוב מקבלים כל הזמן נקודות שונות (ובמתמטית: הסדר שלה אינסופי), כך שלא דיברתי כאן “סתם” על הפעולה.

השלב הבא הוא מה שכיניתי השערת בירץ’ וסווינרטון-דייר. מן הסתם גם כדי לתאר את ההשערה הזו צריך פוסט שלם (והרבה יותר מכך), ולכן אסתפק כרגע בתמצית צנועה של החלק שרלוונטי עבורנו - ההשערה עוסקת בעקומים אליפטיים מעל הרציונליים (ומעל הרחבות סופיות של הרציונליים - שדות מספרים - אבל עזבו את זה) וקובעת בין היתר כי מספר הנקודות על עקום שכזה הוא אינסופי אם ורק אם פונקציה מרוכבת מסויימת שמוגדרת עבור העקום - פונקצית ה-\( L \) של העקום, שהיא מעין הכללה של פונקצית הזטא של רימן - מתאפסת בנקודה \( 1 \). זה מעביר את הדיון מעיסוק בעקומים אליפטיים לעיסוק בפונקציות \( L \), שבסופו של דבר מביא לקריטריון של טאנל שהצגתי למעלה. הבעיה היא שהשערת בירץ’ וסווינרטון-דייר היא השערה בלבד, למרות שכל הראיות האמפיריות מצביעות על נכונותה (מה עניין ראיות אמפיריות לכאן? ובכן, בדומה למשפט המספרים הראשוניים או לעניין ה-Monstrous Moonshine שהזכרתי כאן בעבר, גם ההשערה הזו גובשה על בסיס נתונים אמפיריים, במקרה זה שנאספו בידי מחשב). ההשערה הוכחה חלקית, מה שפתר את העניין עבור מספר רב של \( n \)-ים, אך לא עבור כולם. בפרט, משפט של Coates-Wiles מ-79 (אותו ווילס שהוכיח, חמש עשרה שנים לאחר מכן, את המשפט האחרון של פרמה) מוכיח כיוון אחד מהשניים הנדרשים - שאם ישנן אינסוף נקודות על העקום, אז פונקצית ה-\( L \) שלו מתאפסת. מכאן שאם מספר הוא קונגרואנטי, אנו יודעים בודאות כי הוא מקיים את הקריטריון של טאנל; אבל לא מובטח כי כל מספר שמקיים את הקריטריון הוא אכן קונגרואנטי (ומציאת מספר קונגרואנטי שאינו מקיים את הקריטריון תהיה הפרכה להשערת בירץ’ וסווינרטון-דייר!).

אם כן, זוהי (מאוד בגדול) בעיית המספרים הקונגרואנטיים; אבל סיפורם של העקומים האליפטיים לא נגמר כאן, אלא בקושי מתחיל.