מהם המספרים הממשיים?

בהמשך לפוסט הקודם, אני מתחיל כעת בסדרת הפוסטים שתנסה לתאר בצורה פשוטה את יסודות החשבון הדיפרנציאלי והאינטגרלי ברמה שתתאים גם לתלמידי תיכון, ואנחנו חייבים להתחיל מלתאר את ה”עולם” שבו פועל החשבון הזה - עולם שכוכביו הראשיים הם מה שנקרא “המספרים הממשיים” (Real Numbers). כמו שקורה בדרך כלל במתמטיקה, קיימות הכללות רבות של החדו”א לעולמות אחרים, שבהם אין מספרים ממשיים (או שיש הרחבות של המספרים הממשיים - דוגמת המספרים המרוכבים, למי שמכיר) והתוצאה היא תיאוריות יפות ומרתקות; אבל כדי להבין אותן רצוי להבין קודם את המקרה הפשוט של המספרים הממשיים (ואנסה להסביר בהמשך באיזה מובן זהו אכן “המקרה הפשוט ביותר”). הפוסט יהיה ארוך למדי כי אני לא חושב שנכון לפצל אותו לכמה חלקים; אני ממליץ לכם לקחת הפסקה מתישהו.

במושג “מספרים ממשיים” נתקלים כבר בתיכון, ולכן יש לי שאלה לקוראים, בפרט לאלו שחסרים השכלה מתמטית אוניברסיטאית - האם תוכלו להגיד לי מהם המספרים הממשיים? בספרי לימוד תיכוניים לרוב מופיעה הגדרה בסגנון “כל המספרים שעל ציר המספרים” שלא אומרת לנו יותר מדי - מהו ציר המספרים ואיך מחליטים מה מופיע בו בכלל? עם זאת, ההגדרה הזו גם תופסת באופן מסויים תכונה חשובה של המספרים הממשיים - הרצף שלהם, העובדה שאנחנו תופסים את ציר המספרים כולו באמצעותם. גם לזה נחזור מאוחר יותר.

לעת עתה בואו נעשה חזרה מהירה על מהם מספרים בכלל - בראשית ימי הבלוג כתבתי סדרת פוסטים בנושא למעוניינים, וכעת אקצר יותר. המשחק מתחיל עם המספרים \( 1,2,3,\dots \) ודומיהם המוכרים לנו כבר מחיי היום יום - אלו הם המספרים הטבעיים. בשלב הבא אפשר להוסיף למשחק את אפס. בתרבות שלנו, שבה רווח המנהג לקרוא לאנשים “אפס”, המושג נראה לנו טבעי לגמרי - אבל בעבר הוא לחלוטין לא היה מובן מאליו ואפשר לכתוב פוסטים היסטוריים מרתקים (אפילו ספרים) בעניין זה. התכונה שמעניינת אותנו באפס היא שהוא איבר נייטרלי ביחס לחיבור - כאשר מוסיפים אותו למספר, נאמר \( n \), מקבלים שוב \( n \). השלב הבא הוא הוספת מספרים מוזרים עוד יותר - המספרים השליליים. מינוס \( n \) הוא מספר שהתכונה המאפיינת אותו (אפילו המגדירה אותו, במובן מסויים) הוא שכאשר מחברים לו \( n \) מקבלים אפס. גם המספרים השליליים השתרשו בחיי היום יום שלנו זה לא מכבר - יש לנו חוב בבנק, שהוא יתרה של מינוס כך וכך שקלים; יש לנו קומות שמתחת לקומת הכניסה לבניין, שהן קומות מינוס משהו. בדומה, ים המלח נמצא בגובה מינוס 421 מטר ביחס לפני הים.

משיש לנו את כל המספרים הללו, אנחנו מציירים את “ציר המספרים”- קו ישר שבמרכזו 0, ועליו מסומנות נקודות במרווחים שווים. שתי הנקודות הראשונות סביב 0 הן 1 ומינוס 1 (הנוהג הוא ש-1 יופיע מימין ל-0 ומינוס 1 משמאל). שתי הנקודות הבאות הן 2 ומינוס 2, וכן הלאה. קו הוא יצור “רציף”- ציירנו אותו במשיכת עט בודדת, בלי להרים את העט מהדף. לכן אינטואיטיבית ניתן לחשוב שכל נקודה על ציר המספרים - לא רק אלו שסימנו במיוחד - מסמנת מספר, ולכל המספרים שמתקבלים כך לקרוא “מספרים ממשיים”. למי שזה מפריע לו (בצדק…) אפשר לנקוט בגישה קצת יותר פורמלית - להגיד שנקודה כלשהי על חלקו הימני של הציר מסמנת מספר שמתאים לאורך של הקטע שבין נקודה זו ובין 0 (ונקודה על חלקו השמאלי מתאימה למינוס האורך של קטע זה). אם אנחנו יוצאים מנקודת הנחה שאורכים של קווים הם משהו “אמיתי”, ושנכון להגדיר מספרים על פיהם, האינטואיציה שלנו מפוייסת מאוד; כמובן שזו עדיין לא הגדרה מתמטית-פורמלית, אבל זו ההגדרה שאליה ספרי הלימוד מכוונים - והיא לא כל כך גרועה, בהתחשב בכמה שהסיפור האמיתי מסובך יותר.

כעת אנחנו מרחיבים את המספרים שלנו על ידי הכנסת שברים לתמונה. נניח שניקח בציר המספרים את הקטע שבין 0 ל-1, ונשים בו נקודה חדשה בדיוק באמצע - איזה מספר הנקודה הזו תייצג? אפשר לחשוב על זה כך - היחס שבין מרחק הנקודה הזו מאפס, לבין מרחק הנקודה 1 מאפס, הוא בדיוק 1 ל-2; כלומר, המרחק של הנקודה הזו מאפס נכנס בדיוק פעמיים במרחק של 1 מאפס. כותבים את זה \( \frac{1}{2} \) וקוראים לזה “חצי”, או “1 חלקי 2”.

באופן דומה אפשר לסמן שתי נקודות במרווחים שווים בקטע שבין 0 ו-1, ולקבל את \( \frac{1}{3} \) ו-\( \frac{2}{3} \) (למה?). ובאופן כללי אפשר לסמן \( n \) נקודות במרווחים שווים ולקבל את המספרים \( \frac{1}{n},\frac{2}{n},\dots,\frac{n-1}{n} \). ולא חייבים להסתפק בקטע שבין 0 ו-1. למשל, אם נסמן נקודה בדיוק באמצע הדרך בין 1 ו-2, נקבל את \( \frac{3}{2} \); הרעיון כאן הוא שאם נחבר קטע זה לעצמו פעמיים, נקבל בדיוק את 3. בצורה הזו קיבלנו את כל השברים מהצורה \( \frac{a}{b} \) כאשר \( a,b \) שניהם מספרים שלמים (אין בעיה עם זה שהם יהיו שליליים), פרט למקרה אחד בעייתי - אין משמעות לכל המשחק הזה אם \( b=0 \). למשל, \( \frac{1}{0} \) היה צריך להתפרשן אצלנו בתור “אורך הקטע שכאשר מסתכלים על 0 עותקים סמוכים שלו, מקבלים את 1”, אבל לא קיים כזה קטע - 0 עותקים של קטע כלשהו הם 0, ולעולם לא יהיו 1. אם כן, מדוע לא לומר ש-\( \frac{0}{0}=0 \), משהו שאוסרים עליו במפורש בתיכון? ובכן, כי הגדרה כזו תשבור את חוקי החשבון שאנחנו מכירים. אם אנחנו רוצים לחבר את \( \frac{a}{b},\frac{x}{y} \) אנחנו משתמשים במה שנקרא “מכנה משותף” - את \( \frac{a}{b} \) אנו כופלים ומחלקים ב-\( y \) ומקבלים \( \frac{ay}{by} \). ל-\( \frac{x}{y} \) אנחנו מעניקים טיפול דומה ומקבלים את \( \frac{bx}{by} \), ועכשיו יש לנו מכנה משותף לשני המספרים ואפשר לחבר אותם “כרגיל”ולקבל \( \frac{ay+bx}{by} \). אם ננסה להפעיל את זה על \( \frac{0}{0} \) יקרה הדבר המוזר הבא: \( \frac{a}{b}=\frac{a}{b}+0=\frac{a}{b}+\frac{0}{0}=\frac{a\cdot0+b\cdot0}{b\cdot0}=\frac{0+0}{0}=\frac{0}{0}=0 \). כלומר, קיבלנו שכל מספר שווה לאפס - ואנחנו לא רוצים שדבר כזה יקרה. לכן ההגדרה של \( \frac{0}{0}=0 \) היא ממש הרסנית אם אנחנו לא משנים את כללי החשבון שלנו בהתאם - וכללי החשבון שלנו יקרים לנו בהרבה מאשר האפשרות לתת שם אחר לאפס. אגב, שימו לב שהשתמשתי כאן בכך ש-\( a\cdot0=0 \) לכל \( a \); האם אתם יכולים להוכיח זאת ממש, על פי כללי החשבון? (אפשר, וההוכחה אפילו אינה כה מסובכת אף כי יכול להיות בעייתי לגלות אותה בלי נסיון קודם בתעלולים כאלו).

נראה ששברים מסיימים לנו את העניין. יש להם את התכונה היפה שבין כל שני שברים קיים עוד שבר (להבדיל, בין המספרים השלמים 1 ו-2 לא קיים עוד מספר טבעי) - למשל, אפשר לקחת את הקו שמחבר את שתי הנקודות על ציר המספרים שמתאימות השברים ואז להסתכל באמצע שלו - גם נקודה זו תהיה שבר. הדעת נותנת שכל נקודה על ציר המספרים תוכל להתקבל באופן שכזה. אלא שזה לחלוטין לא נכון. כאן אני קופץ לחומר שלא בהכרח מראים בבית הספר - לא כל המספרים על ציר המספרים הם שברים. למעשה, רובם לא. עבורי, ההבנה של הדבר הזה (שלא הבנתי כלל בתיכון, וגם לא נתתי עליו את דעתי כלל) הייתה אחת מנקודות הציון החשובות בדרך שלי להתאהבות במתמטיקה.

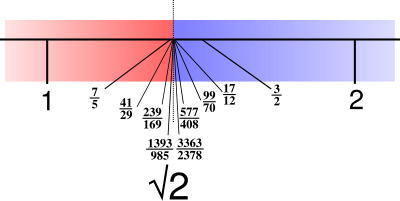
אם כן, אילו מספרים אינם שברים? למשל, \( \sqrt{2} \) אינו שבר. אם נצייר ריבוע שאורך צלעו הוא 1, אז אורך אלכסונו יהיה \( \sqrt{2} \) (ממשפט פיתגורס), כך שבבירור \( \sqrt{2} \) הוא אורכו של קטע “חוקי” כלשהו, ולכן - על פי ההגדרה שלנו - מספר ממשי. אלא שכל נסיון לכתוב את \( \sqrt{2} \) כשבר יוביל לסתירה. הראיתי בעבר את ההוכחה לכך, והנה תקציר: אם \( \sqrt{2}=\frac{a}{b} \) אז \( 2=\frac{a^{2}}{b^{2}} \), כלומר \( a^{2}=2b^{2} \), ומכיוון שהריבוע של \( a \) זוגי גם הוא זוגי, כלומר \( a=2c \), כלומר \( 4c^{2}=2b^{2} \), כלומר \( 2c^{2}=b^{2} \), ומכיוון שהריבוע של \( b \) זוגי, גם \( b \) זוגי. מכאן שגם \( a \) וגם \( b \) זוגיים. אבל אם כך היה הדבר, אפשר היה לחלק את שניהם ב-2 ולקבל מ-\( \frac{a}{b} \) שבר אחר (שבו המונה והמכנה קטנים יותר) וגם הוא שווה ל-\( \sqrt{2} \), וגם בו המונה והמכנה שניהם מתחלקים ב-2. אבל אי אפשר לחזור על התעלול הזה לנצח כי בכל פעם המונה והמכנה קטנים (ושניהם שלמים חיוביים) ולכן בסוף בהכרח נגיע לסתירה (כלומר, ניווכח שלא ייתכן שגם \( a \) וגם \( b \) זוגיים). ההוכחה הזו היא דוגמה מובהקת להוכחה מתמטית “אמיתית” - יש בה הנחה בשלילה, יש בה תעלול רעיוני מחוכם למדי של “נצא ממצב מסויים ונגיע למצב דומה לו, אבל עם מספרים קטנים יותר - וזה תהליך שאי אפשר לחזור עליו לנצח” (רעיון זה נפוץ מאוד במתמטיקה), וכן - יש בו גם טיפה טכניקה.

באופן דומה ומחוכם קצת יותר אפשר להראות שגם \( \sqrt{n} \) הוא לא שבר עבור כל \( n \) שאיננו ריבוע של מספר טבעי. אבל הסיפור לא נגמר במספרים כאלו בלבד. למשל, גם השורש השלישי של 2 איננו שבר, והרביעי וכן הלאה. והמצב מסובך עוד יותר: שורש של \( n \) הוא בסך הכל פתרון של המשוואה \( x^{2}=n \), ומה שאמרנו כאן הוא שאין למשוואה הזו פתרון שהוא שבר. אבל יש עוד המון משוואות בעולם, למשל \( x^{2}+x-1=0 \), וגם למשוואה זו אין פתרון שהוא שבר, אבל הוא כן נמצא על ציר המספרים הממשיים (איך רואים דבר כזה? ובכן, משוואה כזו מגדירה את מה שנקרא פרבולה, שהיא עקומה בעלת צורה מסויימת. אם מציירים אותה במישור רואים שהיא חותכת את ציר המספרים בשתי נקודות - אלו הם ה”פתרונות” של המשוואה). אלו מכם שנוסחת השורשים עוד לא נמאסה עליהם לחלוטין יוכלו לראות שפתרון למשוואה הוא \( \frac{-1+\sqrt{5}}{2} \) - כלומר משהו שמערבב שברים עם שורשים. וגם כאן הסיפור עוד לא נגמר ואפשר לדבר על יצורים מסובכים עוד יותר. הבה וניקח למשל מעגל שאורך קוטרו הוא בדיוק 1 - מהו היקפו? אם מקבלים זה שההיקף גם הוא מספר ממשי, אפשר להראות (וזה כבר קצת מאתגר) שהיקף זה איננו שבר, ואפשר גם להראות (וזה כבר ממש מאתגר) שהיקף זה אפילו איננו פתרון של משוואה (פורמלית - משוואה שמקדמיה הם בעצמם שברים). להיקף זה יש שם שבו הוא מוכר קצת יותר טוב: \( \pi \).

התגלית הזו, שקיימים מספרים שאינם שברים, מיוחסת לפיתגוראים (פיתגורס ותלמידיו - לא ברור מי גילה מה). גרסא אחת מדברת על \( \sqrt{2} \) שמגיע מריבוע; גרסא אחרת מדברת על \( \sqrt{5} \) שמופיע בפנטגרם, ובכל מקרה ההוכחה היא גאומטרית באופיה ולא זהה להוכחה שתיארתי למעלה. האגדה מספרת שאחד מתלמידיו של פיתגורס - היפאסוס - גילה את התגלית הזו לעולם הרחב והוטבע בשל כך על ידי הפיתגוראים; הפיתגוראים ביססו את תפיסת העולם שלהם על כך שכל מספר ניתן להצגה כיחס בין שני שלמים, והתגלית הזו ערערה אותם. כך נוצרה הבדלה בין מספרים שניתן להביע בתור יחס כזה, שנקראו מספרים רציונליים (כאשר רציו כאן פירושו ככל הנראה יחס והשם ככל הנראה אינו מרמז שהמספרים הללו “הגיוניים” יותר מאחרים - אם כי קראתי גם טענות שטוענות אחרת), וכאלו שלא - “אי רציונליים”. הממשיים הם המספרים הרציונליים והאי רציונליים יחדיו, אבל זוהי כמובן אמירה ריקה כי לא ברור אילו מספרים אי רציונליים קיימים בכלל. אם אתם תוהים כעת מדוע הממשיים נקראים “ממשיים”- ובכן, ככל הנראה כדי להנגיד אותם למספרים הדמיוניים (למי שלא מכיר - יש דבר כזה), ואם זו אכן הסיבה מדובר בתקלה היסטורית מצערת שכבר מאוחר מדי לשנות.

בתקופת היוונים, מספרים נתפסו כאורכים של קטעים, כך שלאפס ולמספרים שליליים לא הייתה משמעות רבה. עם השנים והתהפוכות שהמתמטיקה עברה, גם אופן ההתייחסות למספרים השתנה, כשלמהפך החשוב ביותר אחראית שיטת הספרה שהשתרשה בסופו של דבר - ייצוג מספרים באמצעות ספרות, כאשר הערך שאותו כל ספרה מייצגת תלוי במיקום שלה בייצוג. למשל, 21 פירושו “עשרים ואחד” ואילו 12 פירושו “שניים-עשר” למרות ששני הייצוגים הללו מכילים בדיוק את אותן הספרות. ההבדל הוא ששתיים מייצג את ספרת העשרות בייצוג הראשון, ואת ספרת האחדות בייצוג השני. כיום הדברים הללו די מובנים מאליהם עבורנו, שכן הורגלנו אליהם; אבל בשעתו הייתה זו דרך הצגה חדשנית ורבת עוצמה, שפישטה עד מאוד את היכולת לבצע חישובים אריתמטיים (שעד כה נעשו במהירות באמצעות כלי עזר דוגמת חשבוניה - בציור רואים תחרות של ממש שנערכה בין משתמש חשבוניה ו”אלגוריסט” שהשתמש באריתמטיקה) בעוד ששיטת הייצוג שהייתה רווחת עד אז, באמצעות ספרות רומיות (שבהן אין את הרעיון של קביעת ערך על פי מיקום - \( \mbox{I} \) הוא תמיד המספר 1, אם כי לעתים מופע שלו במספר אומר שצריך לחסר אותו ולא לחבר אותו) הייתה מסורבלת ולא צלחה לכאלו מטלות.

ראוי להעיר כאן שהרעיון של ספרות שערכן נקבע לפי מקומן היה ידוע כבר לבבלים ולבני המאיה (הם השתמשו בבסיסי הספירה 60 ו-20 בהתאמה, בעוד שאצלנו משתמשים בבסיס 10; מן הסתם בבסיסים אלו יש המון “ספרות” ולכן כל ספרה יוצגה באופן דומה לשיטה הרומית), אך השיטה “שלנו” הומצאה בידי ההודים אי שם במאה ה-6 לספירה, ורק במאה ה-9 לספירה התגלתה למערב בזכות המתמטיקאי הפרסי אל-ח’ואריזמי - אולי חשוב המתמטיקאים של תקופת ימי הביניים, שבה המתמטיקה האירופאית (שכה פרחה בימי היוונים העתיקים) הייתה מצויה בעידן חושך משלה, בעוד התרבות המוסלמית היא זו שקידמה את המתמטיקה בימים הללו.

בשיטה העשרונית הספרה הראשונה מייצגת אחדות, השנייה מייצגת עשרות וכן הלאה - אבל איך מייצגים שברים? כותבים נקודה בתוך המספר, ואז הספרה הראשונה שמימין לנקודה מייצגת עשיריות, הספרה השניה מייצגת מאיות וכדומה. כך למשל \( 0.123 \) מייצג את המספר \( \frac{1}{10}+\frac{2}{100}+\frac{3}{1000}=\frac{123}{1000} \). אנחנו לומדים בבית הספר איך לכתוב שברים בצורה עשרונית באמצעות חילוק ארוך עם שארית; ומהר מאוד מגלים שיש מספרים שבהם העסק לא נגמר ויש להם אינסוף ספרות אחרי הנקודה. כך למשל \( \frac{1}{3}=0.333\dots \) (שלוש הנקודות אומרות “כאן המספר לא נגמר אלא ממשיך וממשיך”). תזכורת קצרה לגבי האופן שבו זה קורה עבור \( \frac{1}{3} \): אנחנו לא יכולים לחלק את 1 ב-3 כי 1 קטן מדי, ולכן אנו כותבים 0 (1 נכנס ב-3 0 פעמים) ונותרים עם שארית 1. כעת אנו מכפילים את השארית הזו ב-10 ומקבלים 10; וכעת אפשר לחלק את זה ב-3 ומקבלים 3 (שאותו אנו כותבים מייד אחרי הנקודה) ושארית 1. גם את השארית הזו כופלים שוב ב-10 ומחלקים ב-3, ושוב מקבלים תוצאה 3 ושארית 1, וכן הלאה וכן הלאה; בבירור אפשר להמשיך עם תהליך החלוקה הזה לנצח ובכל פעם נקבל תוצאה 3 ושארית 1. אנחנו “תקועים בלולאה אינסופית”.

אפשר להראות שכל מספר רציונלי שננסה לכתוב כשבר עשרוני יתנהג כך - או שהכתיבה שלו תהיה סופית (כמו \( \frac{123}{1000} \) מיודענו) ואז אפשר לחשוב עליו כאילו מרגע מסויים מופיעים בו רק אפסים (כלומר, \( 0.123=0.123000\dots \)), או שהכתיבה שלו תהיה אינסופית, אך מחזורית - תהיה קבוצת ספרות כלשהי שפשוט תחזור על עצמה מרגע מסויים ועד אינסוף. אבל כדאי לשים לב שאפשר לכתוב מספרים עשרוניים אינסופיים שאינם מחזוריים באופן הזה, למשל \( 0.101100111000\dots \) שבו בהתחלה מופיע \( 10 \), אחר כך \( 1100 \) ובאופן כללי - מופיעה סדרה באורך \( n \) של אחדות, אז סדרה באורך \( n \) של אפסים, אז סדרה באורך \( n+1 \) של אחדות, וכן הלאה. אתם מוזמנים להציע עוד מספרים לא מחזוריים משל עצמכם (ויש דברים יצירתיים שאפשר להציע למשל, מספר שבו יש 0 אחרי הנקודה למעט בספרות שהמיקום שלהן הוא ראשוני, ושם יש 1), אבל אני מניח שכבר הבנתם את הרעיון - מצאנו דרך תיאור כלשהי למספרים שאינם רציונליים. הגישה של המתמטיקאים במשך שנים רבות הייתה לחשוב על כל סדרה כזו כמספר לגיטימי; ולמעשה, זה המצב גם כיום, אך כבר איננו בוחרים להגדיר את המספרים הממשיים באופן זה, בגלל קשיים טכניים שהדבר יוצר (איך מחברים שני מספרים אינסופיים? הרי החיבור צריך להתחיל מהקצה הימני!).

רק לקראת סוף המאה ה-19, הציעו שני מתמטיקאים דרכים מדוייקות “לבנות” את המספרים הממשיים, ובשני המקרים הבנייה התבססה על המספרים הרציונליים. שניהם הושפעו מהרוח שנשבה במאה ה-19 וכבר תיארתי בפוסט הקודם, של הגברת הדיוק (מילה אהובה על מתמטיקאים בהקשר הזה היא “ריגורוזיות”) של המתמטיקה. ריכארד דדקינד המציא את הבניה שלו כבר ב-1858 אך לא טרח לפרסם אותה שכן לא חשב שיש בה עניין גדול לקהילה המתמטית. רק כאשר גאורג קנטור פרסם ב-1872 את הגישה שלו דדקינד חש שגם לו יש מה להציע ופרסם את רעיונותיו. שתי הבניות הן שונות באופיין ולכל אחת הכללות משל עצמה; אציג כאן את זו של דדקינד שכן זו של קנטור מצריכה מושגים שכדי להבין אותם צריך להכיר קצת חדו”א קודם כל. עם זאת, אני רוצה לחכות מעט עם הבניה ולפני כן לשאול את עצמנו - מה בעצם אנחנו רוצים להשיג?

בשורה התחתונה אנחנו רוצים לעשות חדו”א. עוד לא אמרתי מה זה חדו”א, כך שלא ברור מה בעצם אנחנו צריכים, אבל אני יכול לרמוז - במערכת המספרים שבה נעבוד, יהיה הכרחי עבורנו שנוכל לבצע חיבור, חיסור, כפל וחילוק. את זה אי אפשר לעשות רק עם המספרים השלמים, למשל (אי אפשר לחלק את 1 ב-2 ולקבל מספר שלם) אבל בהחלט אפשר לעשות עם הרציונליים. לקבוצה שבה אפשר לבצע את פעולות החשבון הללו והן מתנהגות “כפי שאנחנו מצפים מהן” (כלומר: מקיימות את חוקי החילוף, הקיבוץ והפילוג, 0 הוא נייטרלי לחיבור ו-1 הוא נייטרלי לכפל) קוראים שדה. אם כן, אנו רוצים לעבוד בתוך שדה, לכל הפחות. אפשר היה להגיד כעת שנזדקק גם להוצאות שורש, אבל זה לא כל כך נכון - לא באמת נזדקק להוצאות שורש. אם כן, למה הכרחי למי שעוסק בחדו”א להגדיל את המספרים הרציונליים? זו אינה שאלה טריוויאלית כלל. כדאי להעיר כאן שהרבה דברים יפים במתמטיקה נעשים תוך התמקדות במספרים הרציונליים ובשדות שמקבלים מהם אחרי שמוסיפים להם מספר מוגבל של שורשים (למשל, מסתכלים על שדה כל המספרים מהצורה \( a+b\sqrt{2} \) כאשר \( a,b \) רציונליים). זהו, למשל, התחום שבו עוסקת תורת המספרים האלגברית (שהיא תחום מתקדם יותר במתמטיקה מאשר החדו”א שעליו אדבר). אם כן, הממשיים אינם הכרחיים לצורך עיסוק “כללי” במתמטיקה. אבל בחדו”א מתבססים לעתים קרובות על תכונה של הממשיים שמכונה “אקסיומת החסם העליון”. כדי להסביר מדוע מסתמכים עליה ובאיזה מקומות הצורך הזה צץ, צריך להעמיק קצת בחדו”א ולא אוכל לעשות זאת כרגע; בינתיים אתאר את האקסיומה עצמה (לא להתבלבל - “אקסיומה” במובן המתמטי המודרני אינה משהו שהוא מובן מאליו לכל; זהו פשוט דרך להגיד “תכונה שאנו מצפים שתתקיים באובייקט שעליו אנחנו מדברים, ואם הוא לא מקיים אותה אין משחק”).

תכונה אחת של המספרים שטרם דיברתי עליה כלל היא קיום סדר עבורם. ניתן להשוות כל שני איברים ולהגיד מי מהם גדול יותר. 1 גדול מ-0 ובוודאי שגדול ממינוס 1, אבל קטן מ-2. מסמנים \( a\le b \) אם \( a \) קטן או שווה ל-\( b \). גם ברציונליים נשמרת תכונת הסדר הזו, ואנו רוצים שגם בממשיים היא תתקיים. כעת, אם נתונה קבוצה כלשהי של מספרים, אז כל מספר שגדול מכל המספרים בקבוצה מכונה “חסם מלמעלה” (או “חסם מלעיל” כמו שאוהבים לומר לפעמים) של הקבוצה. למשל, 0 הוא חסם מלמעלה של קבוצת כל השליליים; לקבוצת כל החיוביים אין חסם מלמעלה; קבוצת “כל השנים שבהן מכבי ת”א זכתה באליפות” חסומה מלמעלה על ידי, נניח, 3,000; אבל גם על ידי 2,100 וכדומה. אם כן, לקבוצה \( A \) יכולים להיות הרבה מאוד חסמים, ואנחנו יכולים לדבר על (זהירות, הגענו לקטע מבלבל) - החסם מלמעלה הקטן ביותר של הקבוצה \( A \). החסם הזה (המינימום של קבוצת כל החסמים מלמעלה של \( A \)) נקרא החסם העליון של \( A \), ובעברית - הסופרמום (קרי: סופרימום) של \( A \), ומסמנים אותו כ-\( \sup A \).

וכעת לפאנץ’, עוד לפני שתספיקו לשאול את השאלה. אם אנחנו מגבילים את העולם שלנו למספרים רציונליים, ישנן קבוצות שחסומות מלמעלה אך אין להן חסם עליון. והנה הדוגמה: קבוצת כל המספרים הרציונליים הקטנים מ-\( \sqrt{2} \), ובכתיב מתמטי: \( A=\left\{ a\in\mathbb{Q}|a<\sqrt{2}\right\} \). זהו סימון סטנדרטי אך קשה למי שאינו מכיר - האות \( \mathbb{Q} \), מהמילה Quotient, מייצגת את הרציונליים; \( \in \) מייצג “שייך ל-“, והקבוצה מתוארת באמצעות שני חלקים. צריך לקרוא אותה משמאל לימין ואז יוצא משהו בסגנון “כל המספרים הרציונליים אשר מקיימים (ופה מגיע החלק השני) שהם קטנים מ-\( \sqrt{2} \)). קרוב לודאי שחלק מכם יתרגזו כעת, ובצדק, על ההגדרה הטיפשית הזו - אמרתי ש-\( \sqrt{2} \) איננו רציונלי אבל עכשיו אני מתעקש לדבר רק על רציונליים, ולכן “אסור” לי בכלל לאזכר את \( \sqrt{2} \)! אין בעיה, אני אומר, אז נשנה את הגדרת \( A \) באופן הבא: \( A=\left\{ a\in\mathbb{Q}|a^{2}<2\right\} \). עם הגדרה זו אין בעיה של ממש והיא תופסת בדיוק את אותם האיברים פרט למספרים שליליים קטנים מספיק, שממילא לא מעניינים אותנו.

למה אין ל-\( A \) חסם עליון? הבה וניקח מספר רציונלי חיובי כלשהו, \( a>0 \). אז אנחנו יודעים ש-\( a^{2}\ne2 \). נניח לרגע ש-\( a^{2}<2 \), אז אני טוען שקיים \( b \) רציונלי כך ש-\( a<b \) ועם זאת \( b^{2}<2 \). והדרך שבה אני הולך להוכיח זאת כבר תהיה דרך חדו”אית למהדרין - זו ההזדמנות הראשונה שלנו לראות את סגנון ההוכחות שהולך בחדו”א.

אני אגדיר את \( b \) להיות המספר הבא: \( b=a+\delta \), כאשר \( \delta \) (האות היוונית דלתא) הוא מספר רציונלי שאני טרם מתחייב על גודלו. בינתיים נחשוב עליו כעל משתנה, ועוד מעט נחליט מה הוא יהיה על פי מה שיהיה לנו נוח; לעת עתה אני רק דורש ש-\( \delta>0 \) ולכן אכן מתקיים ש-\( b>a \); וש-\( \delta \) רציונלי ולכן גם \( b \) רציונלי (סכום של שני רציונליים הוא רציונלי). כעת, אני רוצה שיתקיים \( b^{2}<2 \), כלומר שיתקיים \( \left(a+\delta\right)^{2}<2 \). לאחר פתיחת סוגריים אקבל שאני רוצה שיתקיים \( a^{2}+\delta\left(2a+\delta\right)<2 \).

עכשיו אשתמש בתעלול כדי להיפטר מה-\( \delta \) שבסוגריים. עוד לא בחרתי את ערכו של \( \delta \) אבל אתם אולי מרגישים כבר כעת שאני רוצה שהוא יהיה קטן. אם כן, אין לי בעיה להוסיף עוד הנחה למשחק: \( \delta<a \). מכאן ש-\( \delta\left(2a+\delta\right)<\delta\cdot3a \), ולכן אם אראה ש-\( a^{2}+\delta\cdot3a<2 \) מתקיים עבור \( \delta \) כלשהו, הראיתי גם ש-\( a^{2}+\delta\left(2a+\delta\right)<2 \) מתקיים עבורו. שימו לב להזנחה הזו! היא מקלה עלי את החיים מבחינה טכנית, ולא פוגמת כלל בנכונות ההוכחה. הקושי שב”התרגלות” לביצוע הזנחות שכאלו הוא אחד מהקשיים העיקריים של סטודנטים באוניברסיטה כשהם מתמודדים לראשונה עם חדו”א. בלי לזהות מקומות שבהם אפשר “להקל על החיים” כך, התרגילים הטכניים הקשים של חדו”א אוניברסיטאית הופכים לקשים פי כמה.

נמשיך. אני רוצה למצוא \( \delta \) כך ש-\( a^{2}+\delta\cdot3a<2 \). זה כבר תרגיל אי שוויונים תיכוני: מעבירים אגף, מחלקים, ומקבלים \( \delta<\frac{2-a^{2}}{3a} \). מכיוון ש-\( a^{2}<2 \) (כך הנחנו - זוכרים?) הרי שהמספר באגף שמאל הוא גדול מאפס. בנוסף, \( a \) רציונלי ולכן גם הוא עצמו רציונלי; לכן אפשר פשוט לבחור \( \delta=\frac{1}{2}\cdot\frac{2-a^{2}}{3a} \) ולקבל את מה שרצינו: \( \delta \) שהוא גם גדול מאפס וגם מקיים את אי השוויון שנדרש בהתחלה. וכעת אפשר… לא, לא, לא! לא כל כך מהר. מה פספסתי? ובכן, שכחתי את ההנחה ש-\( \delta<a \) שהוספתי לעצמי קודם. זו לא בעיה - אני אגדיר את \( \delta \) להיות המספר הקטן יותר מבין זוג המספרים \( \frac{1}{2}\cdot\frac{2-a^{2}}{3a} \) ו-\( \frac{1}{2}\cdot a \). אבל זה בור שצריך להכיר ולא ליפול לתוכו.

תמה לה ההוכחה. מצד אחד, זו הוכחה טכנית. מצד שני, היא שונה מאוד באופייה מתרגיל תיכוני רגיל. בפרט שימו לב להזנחה שביצעתי באמצע, לכך שכל התרגיל הוא עם הפרמטר \( a \) שלא נראה שמשרת מטרה כלשהי, ולכן שהפתרון הסופי נראה מכוער לאללה (\( \frac{1}{2}\cdot\frac{2-a^{2}}{3a} \)) וזה ממש לא מפריע לי ואני לא מחפש דרך “לפשט” אותו. אבל ההבדל האמיתי הוא שלתרגיל הזה הייתה מטרה - אני מנסה לשכנע אתכם שלקבוצה כלשהי אין חסם עליון.

ובכן, הראיתי שאם \( a \) הוא רציונלי בתוך \( A \) עצמה, אז קיים רציונלי אחר בתוך \( A \) שגדול ממנו; מכאן שאם יש ל-\( A \) חסם עליון, הוא לא יכול להיות איבר של \( A \) עצמה. אבל אם \( a^{2}>2 \) אז בהוכחה דומה מאוד לזו שנתתי (תבחרו \( b=a-\delta \)) אפשר להראות שקיים \( b \) רציונלי כך ש-\( b^{2}>2 \) ועם זאת \( b<a \). בגלל ש-\( b^{2}>2 \) אז \( b \) הוא חסם מלמעלה של \( A \); ולכן הראיתי כרגע ש-\( a \) איננו חסם עליון של \( A \), כי קיים חסם מלמעלה אחר שקטן ממנו. המסקנה: \( a \) היה יכול להיות חסם עליון של \( A \) רק אם הוא היה מקיים \( a^{2}=2 \), אבל אין מספר רציונלי שמקיים זאת. סוף הסיפור.

אם כן, מה החסם העליון של \( A \)? כמובן, \( \sqrt{2} \). ההוכחה שנתתי למעלה “נשברת” כשמפעילים אותה על \( a=\sqrt{2} \) פשוט כי \( 2-a^{2}=0 \). לכן לקבוצה \( A \) כן יש חסם עליון אם מכניסים למשחק את \( \sqrt{2} \). ועכשיו אפשר סוף סוף להגדיר את הממשיים בצורה כמעט פורמלית: הממשיים הם בדיוק המספרים שאנחנו צריכים שיהיו במשחק כדי שלכל קבוצה (לא ריקה) שחסומה מלמעלה יהיה חסם עליון. התכונה הזו, “לכל קבוצה לא ריקה חסומה מלמעלה יש חסם עליון” היא מה שנקרא “אקסיומת החסם העליון”. העובדה שהרציונליים לא מקיימים את האקסיומה הזו מצביעה שבמובן מסויים, בקבוצת הרציונליים יש “חורים” והיא לא תופסת את כל הישר הממשי, בעוד שבקבוצת הממשיים שכן מקיימת אותה אין חורים כאלו - היא “רציפה”.

הזכרתי כבר קודם את המושג “שדה” והערתי שהרציונליים והממשיים שניהם שדות. אם מוסיפים לתמונה את היכולת להשוות בין כל שני איברים, השדה הופך לשדה סדור. המספרים הממשיים הם השדה הסדור היחיד בו מתקיימת אקסיומת החסם העליון (כלומר, אפשר להוכיח שאם יש שני שדות סדורים שמקיימים את אקסיומת החסם העליון, הם “אותו הדבר” במובן שלא אציג כאן באופן מדויק). מנקודת מבט מתמטית, זוהי ההגדרה של המספרים הממשיים; מה שדדקינד וקנטור עשו היה להציג בניות של הממשיים באמצעות אבני בניין פשוטות יותר, שהראו שההגדרה אינה ריקה מתוכן אלא באמת קיים אובייקט העונה לתנאי ההגדרה. קנטור ודדקינד שניהם מגיעים אל אותו האובייקט, אך בדרכים שונות. קשה להסביר פורמלית בשלב זה למה הכוונה ב”מגיעים אל אותו האובייקט בדרכים שונות” (כי אם מסתכלים על התוצר הסופי ה”יבש” של מה שהם עשו, הוא לא נראה זהה) ולכן אסתפק בהצגת הבניה של דדקינד ואסיים בזאת.

דדקינד ממשיך עם הרעיון שאיתו התחלתי קודם, של הקבוצה \( A \) שלא היה לה חסם עליון. הוא מגדיר חתך בתור קבוצה \( A \) של מספרים רציונליים כך שאם \( a\in A \) ו-\( b<a \), אז גם \( b\in A \). במילים, אם \( a \) הוא איבר של \( A \) ו-\( b \) קטן מ-\( a \), אז גם \( b \) שייך ל-\( A \). למה “חתך”? שכן הקבוצה הזו “חותכת” את המספרים הרציונליים לשתי קבוצות - כל מי ששייך ל-\( A \), וכל מי שאינו שייך ל-\( A \) ולכן הוא בהכרח גדול מכל אברי \( A \) (אם \( a \) אינו שייך ל-\( A \) אבל קטן מ-\( b \) שכן שייך ל-\( A \), אז מהגדרת \( A \) גם \( a \) חייב להיות שייך אליה…). על ציר המספרים \( A \) היא קו שנמתח ממינוס אינסוף ואז נעצר איפה שהוא, ומייד אחר כך מתחילה הקבוצה של כל מי שאינו ב-\( A \). השאלה היא רק מה קורה בנקודת החיתוך עצמה.

עוד שתי דרישות שדדקינד דורש מ-\( A \) הוא ש-\( A \) תהיה חסומה, אך שלא תכיל את החסם העליון של עצמה, אפילו אם הוא קיים. כעת דדקינד מגדיר את המספרים הממשיים באמצעות החתכים הללו - כל מספר ממשי מתאים ל-\( A \) כלשהי, כאשר, כפי שניתן היה לנחש, הקבוצה \( A \) מייצגת את המספר שהוא החסם העליון של \( A \). בתמונה אנחנו רואים את החתך שמגדיר את שורש 2.

כאן הכיף רק מתחיל - צריך להגדיר פעולות של חיבור, חיסור, כפל וחילוק על הקבוצות הללו באופן שעדיין יהיה הגיוני, וצריך להוכיח שאקסיומת החסם העליון מתקיימת עבור אוסף הקבוצות הזה. אלו הם פרטיים טכניים לא טריוויאליים שאיני רוצה להפיל עליכם בפוסט הזה; העיקר הוא ברעיון הבניה עצמו, שלדעתי הוא זר ומוזר לכל מה שרואים בתיכון. כמובן, ייתכן שתרגישו ש”מרמים” אתכם בבנייה הזו שלכאורה מניחה את המבוקש; אך אני מבטיח שקריאה זהירה בטקסט שמתאר את הבניה במפורש עשויה להניח את דעתכם שלא מניחים כאן מאום מראש.

אם כן, אלו הם המספרים הממשיים, ומעתה ואילך נוכל לשכוח את רוב הדיון שהתרחש כאן ולחשוב עליהם פשוט בתור “שדה סדור שמקיים את אקסיומת החסם העליון”. אני מקווה שהצלחתי להמחיש כאן שיש בהם מעט יותר מאשר רק “כל המספרים שעל ציר המספרים”.