המלון של הילברט, או - מדוע יש גדלים שונים של אינסוף

אחת מהתוצאות היפות-ועם-זאת-נגישות במתמטיקה היא קיומם של אינסוף גדלים שונים של “אינסוף”. כבר סיפרתי עליה בראשית ימי הבלוג, אבל נראה לי כדאי לתת לה פוסט חדש, שינסה גם להיות נגיש יותר מקודמו; אני מקווה שאת הפוסט הזה יוכלו להבין גם אנשים חסרי כל ידע במתמטיקה, כל עוד יש להם סבלנות ורצון ללמוד.

צריך להתחיל מהשאלה הפשוטה - מהו אינסוף? יש מן הסתם תשובות רבות לשאלה הזו - ספרים לא מעטים נכתבו עליה בדיוק. לכן אדבר רק על המושג שבו יעסוק הפוסט הזה, של אינסוף בתור כמות. אנחנו נוהגים להשתמש במספרים טבעיים כדי למנות כמויות - אחד אלוהינו, שני לוחות הברית, שלושה אבות, ארבע אמהות… אלו שימושים של המספרים 1,2,3,4. באופן יותר מתמטי, אפשר להגיד שאלו גדלים של קבוצות. קבוצת ה”אמהות”, למשל, היא מגודל 4. קבוצת המספרים הטבעיים הזוגיים שקטנים או שווים ל-10 היא מגודל 5: המספרים הם 2,4,6,8,10. אבל כמה מספרים טבעיים זוגיים יש בכלל? ועזבו אותך מזוגיים - כמה מספרים טבעיים יש בכלל? התשובה לשאלה הזו היא “אינסוף”.

אני אוהב להמשיל את האינסוף הזה ל”כמה שתרצה”. נניח שיש לנו מכולה עם 1,000 עגבניות. אם אנשים יבואו ויקחו עגבניות באופן חופשי, מהר מאוד לא ישאר כלום - אחרי ש-1,000 איש ייקחו כל אחד עגבניה אחת, המכולה תתרוקן. אם, לעומת זאת, במכולה היו אינסוף עגבניות, אז לא משנה כמה עגבניות היו לוקחים ממנה, היא לא הייתה מתרוקנת - כמות העגבניות בה הייתה נותרת אינסוף.

המתמטיקאי דיוויד הילברט אהב להמחיש את העניין המוזר הזה עם סיפור על מלון בעל אינסוף חדרים - חדר מס’ 1, חדר מס’ 2, וכן הלאה. למרות אינסוף חדריו, המלון היה הצלחה מסחררת ובתפוסה מלאה, אבל אז בא אורח עיקש ורצה להשתכן בחדר. מנהל המלון מצא פתרון פשוט: הוא ביקש בנימוס מהאורח בחדר 1 לעבור לחדר 2. מהאורח בחדר 2 הוא ביקש לעבור לחדר 3, וכן הלאה. בצורה הזו התפנה מקום חדש בחדר 1, ואף אחד מהאורחים הקיימים לא נותר ללא חדר (אם כי כולם נאלצו לעבור…). המוזרות הזו - הרי זה תעלול שאי אפשר לעשות במלון עם מספר סופי של חדרים - היא מהתכונות המאפיינות של האינסוף.

הילברט ממשיך בסיפור ומספר על תופעות יותר מוזרות. למשל, פתאום בא אוטובוס וממנו יורדים אינסוף אורחים - אורח מס’ 1, אורח מס’ 2 וכן הלאה. מה יעשה בעל המלון עכשיו? יתחכם מעט יותר. מהאורח בחדר 1 הוא יבקש כמקודם לעבור לחדר 2; מהאורח בחדר 2 הוא יבקש לעבור לחדר 4; מהאורח בחדר 3 - לחדר 6. באופן כללי, מהאורח בחדר מס’ \( n \) הוא יבקש לעבור לחדר מס’ \( 2n \) - הוא הכפיל את מס’ החדר. כעת מה קרה? כל האורחים עברו לחדרים הזוגיים במספר, ולכן התפנו אינסוף חדרים - כל החדרים האי-זוגיים. וכעת אפשר לשכן בהם את כל אינסוף האורחים החדשים.

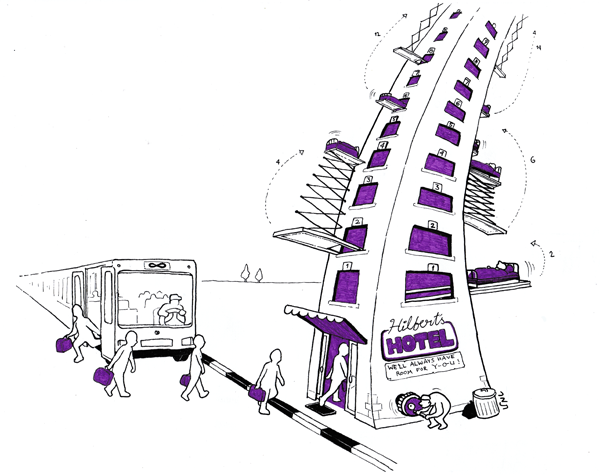
(איור: תמר עקביה)

ועכשיו העלילה מסתבכת עוד יותר - פתאום באים אינסוף אוטובוסים, הממוספרים ב-1,2,3 וכן הלאה; ומכל אוטובוס יורדים אינסוף אנשים - “אורח מס’ 1 מאוטובוס מס’ 1”וכדומה. ומה יעשה בעל המלון המסכן כעת?

בעל המלון כלל אינו מתרגש, מכיוון שהוא יודע תעלול מתמטי נחמד (מי שלא יבין אותו - לא נורא). מספר הוא ראשוני אם הוא מתחלק רק ב-1 ובעצמו. למשל, 2 הוא ראשוני, וכך גם 3,5,7,11 אבל לא 9, למשל, כי 9 מתחלק ב-3 (ומה עם 1? הוא אינו נחשב ראשוני ויש לכך סיבות טובות, אבל זה לא נושא הפוסט). מה שיעניין אותנו בראשוניים הוא שאם ניקח שני מספרים ראשוניים שונים זה מזה, \( p,q \) אז לא רק שהם שונים זה מזה, אלא גם שאם נעלה כל אחד מהם בחזקה מספר מסויים של פעמים (לא בהכרח אותו מספר עבור שניהם) גם התוצאה של זה תהיה בהכרח שונה (בנוסחה מתמטית זה מסומן כ-\( p^{n}\ne q^{m} \) לכל \( n,m \) טבעיים).

אז מה שבעל המלון עושה הוא פשוט - ראשית, הוא מבקש מכל האורחים לעבור לחדר שגדול פי 2 ממספר החדר שלהם, כמקודם. כעת כל החדרים האי זוגיים התפנו. כעת, את האורחים של אוטובוס מס’ 1 הוא משכן בכל החדרים שמספרם הוא חזקה של 3: את אורח מס’ 1 מאוטובוס זה, בחדר מס’ 3; את אורח מס’ 2 בחדר מס’ \( 3^{2}=9 \); את אורח מס’ 3 בחדר מס’ \( 3^{3}=27 \), וכן הלאה. מכיוון שחזקה של מספר אי זוגי היא אי זוגית בעצמה מובטח לנו שאף אורח מאוטובוס מס’ 1 לא יפלוש לחדר של אחד מהאורחים הקיימים במלון.

כעת את אנשי אוטובוס מס’ 2 הוא משכן בחדרים שהם חזקות של 5: \( 5,25,125 \) וכן הלאה. ואת אנשי אוטובוס 3? בחדרים שהם חזקות של 7. ובאופן כללי? את אנשי אוטובוס מס’ \( n \) הוא משכן בחדרים שהם חזקות של הראשוני האי-זוגי ה-\( n \). יש משפט ידוע ולא קשה שמראה כי קיימים אינסוף ראשוניים (וכולם, פרט ל-2, הם אי זוגיים) ולכן ניתן לטפל כך בכל האוטובוסים.

בקיצור, בעל המלון הוא רב תושייה ביותר ושולט היטב במתמטיקה, וזה מוביל אותנו באופן טבעי לשאלה פשוטה - האם יש אתגר שאיתו בעל המלון לא יכול להתמודד? האם ייתכן שיגיעו “יותר מדי” אורחים ובעל המלון יצטרך לוותר? התשובה היא שכן, ושכמות האורחים הזו היא בדיוק אינסוף “גדול יותר” מאשר אינסוף החדרים שיש במלון. זה מביא אותנו לשאלה המרכזית בנושא - איך למדוד “גודל” של קבוצות אינסופיות?

כשמדובר על קבוצה סופית יש דרך פשוטה למדוד את הגודל שלה - פשוט סופרים איבר איבר כמה יש. כשמדובר על קבוצות אינסופיות לא ניתן לעשות זאת כי הספירה לא תיגמר לעולם. לכן משתמשים בקריטריון “השוואתי”- מנסים להגיד כמה איברים יש בקבוצה האינסופיות ביחס לקבוצות אינסופיות אחרות. כדי להבין את העניין כדאי לראות דוגמה עבור קבוצות סופיות: נניח שיש לנו אצטדיון בעל 10,000 מקומות ישיבה והוא מלא אנשים, ואנו רוצים לדעת בערך כמה יש. אפשר לבקש מכל האנשים לשבת ולראות מה קורה - אם נותרו מקומות ישיבה פנויים אז יש פחות מ-10,000 אנשים באצטדיון; אם נותרו אנשים עומדים, יש יותר מ-10,000 אנשים באצטדיון; ואם לא קרה לא זה ולא זה, אנחנו יודעים שיש בדיוק 10,000 אנשים באצטדיון. מה שביצענו כאן הוא התאמה בין האנשים ובין המושבים באצטדיון. כדי שהתאמה תראה שוויון בגודל של קבוצות, היא צריכה לקיים שתי תכונות: ראשית, שלכל אדם יהיה מושב שהוא שלו בלבד והוא לא חולק אותו עם אחרים; ושנית, שלא יהיו מושבים פנויים.

גם בדוגמת המלון ביצענו התאמה - התאמה בין “קבוצת האורחים של המלון” ובין “קבוצת החדרים של המלון”. במקרה שלנו, “קבוצת החדרים של המלון” הייתה פשוט קבוצת המספרים הטבעיים. לקבוצה שאפשר להתאים אותה למספרים הטבעיים - “לשכן במלון של הילברט” - קוראים “קבוצה בת מניה”(כי ניתן למנות את איבריה - לדבר על “איבר מס’ 1, איבר מס’ 2…” וכן הלאה).

כאן מדגדג לי להתחיל לתאר באופן מדויק את התורה המתמטית שמסתתרת מאחורי כל המושגים הללו - אבל זה ירחיק אותי ממטרת הפוסט הזה, שמטרתה בסך הכל לשכנע את הקורא בקיום מספר גדלים שונים של אינסוף. אם כן, מה שאני רוצה להראות היא קבוצת אורחים שהיא גדולה מכדי להיות בת מניה. שלא משנה איך ננסה לשכן אותה במלון של הילברט, תמיד יישאר אורח בלי חדר. למרבה המזל, די קל לתאר את קבוצת האורחים הזו.

לכולנו (רובנו?) יש מספר זהות, ועד כמה שהאסיר יכול להתלונן שהוא אינו מספר אלא אדם חופשי, נוח לפעמים להתייחס אלינו באמצעות מספרי הזהות שלנו. מספר הזהות בישראל הוא בן 9 ספרות, אבל אין בעיה לדבר גם על מספר זהות בן 10 ספרות, או 11, או 12… אבל כל אלו לא יאתגרו את המלון של הילברט, אז אני אציע משהו מוזר: לכל אחד מהאורחים יהיה מספר זהות בן אינסוף ספרות. למי שזה מפריע לו כדאי לזכור שמלכתחילה מלון עם אינסוף חדרים זה לא הכי סביר בעולם, וגם אינסוף אוטובוסים עם אינסוף אורחים לא, אז מה רע בלסבך טיפה את העניינים ולדבר על אורחים שמספר הזהות שלהם הוא אינסופי?

אם כן, בואו נניח שלכל סדרה אינסופית של ספרות יש אורח שמעוניין להשתכן במלון של הילברט. ואני טוען שלא משנה מה בעל המלון יעשה כעת, יהיה אורח שנשאר בחוץ. איך נראה דבר כזה? נניח בשלילה שכל האורחים שוכנו איכשהו במלון, ואז “נבנה” את מספר הזהות של מישהו שבטוח - במאה אחוזים - שלא שוכן במלון. השיטה שבה אני אשתמש נקראת “האלכסון של קנטור” על שם ממציאה (והממציא של כל העיסוק הזה באינסופים).

אז כל האורחים שוכנו במלון. אני הולך לחדר מס’ 1, דופק בדלת, ושואל את האורח שבפנים “סליחה, מה הספרה הראשונה בתעודת הזהות שלך?”. הוא אומר לי, נניח, “7”, אז אני רושם לעצמי על דף נייר “8” וצוחק צחוק מרושע.

ואז אני הולך לחדר 2 ושואל את האורח שבפנים מה הספרה השנייה בתעודת הזהות שלו. הוא אומר לי, נניח, ש-3, ואז אני כותב בדף שלי את הספרה 4 וצוחק צחוק מרושע. כעת כתוב לי בדף 84.

הלאה - חדר 3, האורח אומר לי שהספרה השלישית בתעודת הזהות שלו היא 9, ואני כותב לי 0 בדף וצוחק צחוק מרושע. כעת כתוב לי בדף 840.

בשלב הזה עוצרים אותי אנשים עם חלוקים לבנים ורשתות ושואלים אותי מה אני עושה. אני מסביר להם בנימוס שאני בונה, לאט לאט, מספר זהות של אורח שבודאות לא משוכן במלון. הנה למשל, כל מספר זהות שמתחיל ב-840 הוא בודאות לא מספר הזהות של אורח ששוכן בחדרים מס’ 1, 2 או 3; כי לאורח בחדר מס’ 1, ספרת הזיהוי הראשונה היא 7, ואילו במספר הזהות שאני בונה הספרה הראשונה היא 8; ועבור השני, ספרת הזהות השנייה שלו היא 3, אבל אצלי ספרת הזהות השנייה היא 4; וכן הלאה וכן הלאה. באופן כללי, את האורח מס’ \( n \) אני אשאל על ספרת הזהות ה-\( n \)-ית שלו; כך בכל אורח חדש אני מוסיף ספרה אחת למספר הזהות ואף פעם לא נקלע לקשיים בסגנון “כבר החלטתי מה תהיה הספרה הראשונה בתעודת הזהות אבל על סמך מה שהאורח הנוכחי אמר לי אני חייב לשנות אותה.”, כי כאמור - אני בכל פעם מתעסק בספרה אחרת.

תהליך התשאול הזה מניב סדרה אינסופית של ספרות - כלומר, מספר זהות של מישהו. אותו מישהו, כאמור, לא יכול להיות משוכן באף חדר במלון - כי לכל \( n \), מספר הזהות שלו לא מתאים למספר הזהות של האורח שבחדר \( n \) כי הספרה ה-\( n \)-ית במספרי הזהות שלהם שונה. זה הסוף.

ייתכן שחלקכם צועקים עכשיו שאני רמאי ושקרן ושהחבר’ה בחלוקים הלבנים צריכים לקחת אותי מייד. זה המחיר של להיות לא מדויק - אני יכול לתאר את כל מה שעשיתי כאן בצורה יותר מתמטית-פורמלית, אבל זו לא מטרת הפוסט. יותר מכל, מטרת הפוסט הייתה לגרום לכם להרגיש שקורה כאן משהו מוזר. שהמלון של הילברט יותר מופרע משהיה נדמה במבט ראשון. שיש, במובן מאוד קונקרטי ומוחשי, סוגים שונים של אינסוף, ושבמתמטיקה יש רעיונות שהם מאוד מעניינים ושוברי מסגרות. אני מקווה שהפוסט גם הצליח בזה.