נגזרת - בשביל מה זה טוב? (בעיות קיצון, חלק ב')

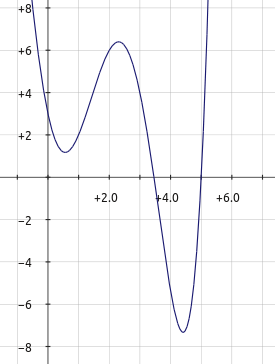
בפוסט הקודם עסקנו בשתי בעיות “מציאותיות” ובסופו של דבר בנינו מודל מתמטי עבורן שבא לידי ביטוי בפונקציה ממשית מסויימת. זה מעביר אותנו לבעיה הכללית הבאה: נתונה פונקציה ממשית \( f\left(x\right) \), ואנו רוצים למצוא ערכי \( x \) שעבורם \( f\left(x\right) \) היא מקסימלית או מינימלית. הנחת היסוד שלנו הוא ש-\( f\left(x\right) \) היא פונקציה “נחמדה” - ניתן לגזור אותה, ולהפיק מהנגזרת מידע על \( f \) עצמה. כמו כן, אם \( f \) גזירה אז היא בפרט רציפה ולכן ניתן לצייר אותה בצורה פשוטה בתור קו אחד רציף. באופן פשטני, פונקציה כזו תיראה בתור קו שעולה למעלה, ואז יורד למטה, ואז שוב עולה, ואז שוב יורד, וכדומה (כמובן, היא יכולה להיות אפילו יותר משעממת - \( f\left(x\right)=x \) היא “קו ישר שכל הזמן עולה”). בואו נסתכל על דוגמה:

מה שאנחנו רואים הוא שלפונקציה יכולות להיות הרבה נקודות מינימום ומקסימום מקומיות. נקודות שאם מסתכלים רק בהן ובסביבה קטנה שלהן, בהן הפונקציה מקבלת את הערך המקסימלי/מינימלי באותה הסביבה. אם אנחנו רוצים להבין איך הפונקציה פחות או יותר נראית, כל הנקודות הללו מעניינות אותנו; ואם אנחנו מעוניינים רק בערך המקסימלי שלה בכלל, גם אז הן מעניינות אותנו - נמצא את כולן ונבדוק באיזו מהן הפונקציה מקבלת את הערך הגדול ביותר.

בואו ננסה להבין מה קורה בנקודת מקסימום, ונחזור לאנלוגיה הרגילה שלנו של “הפונקציה מתארת מיקום, הנגזרת שלה מתארת מהירות, הנגזרת של הנגזרת מתארת תאוצה”. חשבו על כדור שנבעט לו לשמיים - בהתחלה הוא עולה עולה עולה, והעלייה הופכת איטית יותר ויותר, עד שהוא פתאום “נעצר”, ואז מתחיל ליפול. הנקודה שבו הוא נעצר היא נקודת המקסימום שאליה הגובה הגיע. אנחנו יכולים לאפיין אותה באופן הבא: הן מימין והן משמאל לנקודת הזמן הזו, הגובה של הכדור קטן יותר מאשר הוא בנקודת הזמן עצמה. פורמלית, נקודת מקסימום מקומי \( x_{0} \) מקיימת \( f\left(x_{0}-h\right)\le f\left(x_{0}\right) \) ו-\( f\left(x_{0}+h\right)\le f\left(x_{0}\right) \) עבור כל ה-\( h \) החיוביים שהם קטנים מגודל כלשהו (שיכול להיות קטן כרצוננו - כל שאמרנו הוא שצריך שהנקודת תהיה המקסימלית בסביבה כלשהי אך לא דרשנו כלום על גודלה).

כאן נכנס החשבון הדיפרנציאלי לתמונה. מהי הנגזרת של \( f \) בנקודה \( x_{0} \)? כאן אפשר ללכת בדיוק לפי ההגדרה. אם הנגזרת קיימת, אז היא שווה לגבול \( \lim_{h\to0}\frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h} \). כאן \( h \) יכול להיות גם חיובי וגם שלילי, אבל ההבנה שלנו לגבי מה שהולך כאן משתפרת אם אנחנו בוחרים להסתכל על כל אחד מהמקרים לחוד. נסמן ב-\( h\to0^{+} \) את “\( h \) שואף לאפס מימין”, שפירושו ש-\( h \) מקבל ערכים שהולכים ומתקרבים לאפס אבל כולם חיוביים. בדומה נשתמש גם בסימון \( h\to0^{-} \). למי שהסימון הזה עדיין מציק לו בגלל מחסור בפורמליות, הנה הגדרה פורמלית: \( \lim_{h\to a^{+}}g\left(h\right)=L \) אם ורק אם לכל \( \varepsilon>0 \) קיימת \( \delta>0 \) כך שלכל \( a\le h<a+\delta \) מתקיים \( \left|g\left(h\right)-L\right|<\varepsilon \). כעת ארשה לעצמי להשתמש בסימון הזה בחופשיות.

אם כן, מהו \( \lim_{h\to0^{+}}\frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h} \)? אנחנו לא יודעים את הערך המדוייק של הנגזרת, אבל דבר אחד אפשר לומר בודאות - היא קטנה או שווה לאפס. למה? ובכן, כי היצור \( \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h} \) הוא שלילי או אפס תמיד - \( h \) חיובי, אבל המונה תמיד שלילי או אפס ל-\( h \) קטנים מספיק כי \( f\left(x_{0}\right)\ge f\left(x_{0}+h\right) \) לכל ה-\( h \)-ים הקטנים מספיק. גבול של פונקציה שהיא אי-חיובית באיזור הנקודה אליה שואפים גם הוא אי-חיובי (זה תרגיל פשוט להוכיח את זה - אם הגבול דווקא כן חיובי אפשר למצוא סביבה כלשהי של הנקודה אליה שואפים שבה הפונקציה אף היא חיובית).

את אותו תעלול אפשר לעשות גם עבור \( \lim_{h\to0^{-}}\frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h} \) אבל כאן מתהפכים היוצרות - המכנה הוא עדיין אי-חיובי, אבל כעת המונה הוא שלילי (כי \( h \) נלקח מבין המספרים הקטנים מאפס). לכן המנה היא אי-שלילית, ולכן גם הגבול הוא אי שלילי. קיבלנו ש-\( f^{\prime}\left(x_{0}\right) \) הוא מצד אחד אי שלילי, ומצד שני אי חיובי, ולכן \( f^{\prime}\left(x_{0}\right)=0 \). מסקנה: בנקודת מקסימום הנגזרת מתאפסת. באותו אופן מראים גם שבנקודת מינימום הנגזרת מתאפסת. לתוצאה הזו קוראים “משפט פרמה”, אם כי אין הכוונה ל”משפט האחרון של פרמה” המפורסם - פרמה היה מתמטיקאי עסוק וגילה דברים בתחומים רבים, כולל בתחום שרק עשרות שנים אחר כך, בימי ניוטון ולייבניץ, יהפוך להיות החשבון הדיפרנציאלי והאינטגרלי שאנו מכירים.

החישוב היבש שלמעלה הוא לדעתי התחלה לא רעה להבין מה קורה שם ולמה זה נכון, אבל אינטואיציה טובה יותר באה אם חושבים על הנגזרת בתור שיפוע המשיק לפונקציה בנקודה. משיק, זכרו, הוא קו שהכיוון שלו הוא הכיוון שאליו הפונקציה “הולכת”. נקודת מקסימום היא מעין גבעה; עד אליה המשיק הוא בשיפוע חיובי - האף שלו מצביע למעלה. מייד אחרי הגבעה האף של המשיק מצביע למטה. באמצע הדרך המשיק היה צריך להשפיל את האף שלו. דמיינו אותו מסתובב - אי שם באמצע הסיבוב המשיק הוא מאוזן לגמרי. זוהי דוגמה לרציפות: תנועת הסיבוב שהמשיק מבצע היא רצופה - הוא לא “קופץ” לפתע ממצב שבו הוא מצביע למעלה למצב שבו הוא מצביע למטה אלא עובר בכל מצבי הביניים האפשריים, וזה שבו הוא מיושר לגמרי בפרט. מכיוון שחלקיק שניה לפני המצב הזה המשיק עוד מצביע למעלה ולכן הפונקציה עולה, וחלקיק שניה אחרי כן הראש מצביע למטה והפונקציה יורדת, הרגע שבו הוא מאוזן לחלוטין הוא בדיוק בראש הגבעה. משיק מאוזן פירושו שיפוע 0, ולכן נגזרת 0. מכאן האינטואיציה שלי.

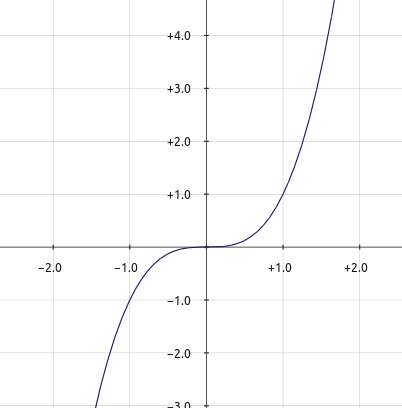
אם כן, שיטת העבודה שלנו כדי למצוא נקודות מינימום ומקסימום היא פשוטה - גוזרים את הפונקציה ובודקים באילו נקודות הנגזרת מתאפסת. כל נקודת מינימום או מקסימום תצוץ כך. לרוע המזל, יש סיכוי שיצוצו עוד נקודות. הביטו בגרף של \( f\left(x\right)=x^{3} \):

בנקודה \( x=0 \) הפונקציה מתיישרת לשניה, והנגזרת (\( 3x^{2} \)) אכן מתאפסת. אבל הפונקציה ממשיכה לעלות גם אחר כך. לפונקציה הזו בכלל אין נקודות מינימום ומקסימום. אז מה קרה כאן? ב-\( x=0 \) היה לפונקציה מה שמכונה “נקודת פיתול”. נקודה שבה היא עוברת מקמירות לקעירות או להיפך; והנה כי כן צריך להבין גם את שני המושגים הללו כדי להבין עד הסוף מה המידע שהנגזרת נותנת לנו.

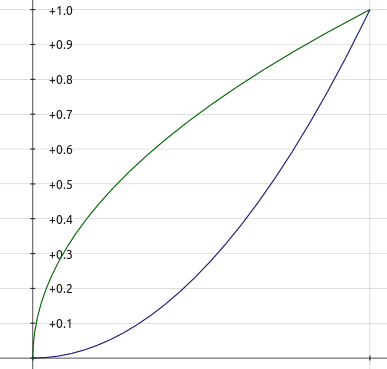
בואו נביט בגרפים של שתי הפונקציות הבאות, \( f\left(x\right)=x^{2} \) ו-\( g\left(x\right)=\sqrt{x} \):

שתיהן פונקציות עולות. שתיהן מקיימות \( f\left(0\right)=g\left(0\right)=0 \) \( f\left(1\right)=g\left(1\right)=1 \), כלומר הן מתחילות מגובה 0 בזמן 0, ומגיעות לגובה 1 בזמן 1, ועם זאת מבט אחד בגרף של שתיהן מבהיר לנו ששתיהן בעלות אופי שונה לגמרי. מה ההבדל? ש-\( f\left(x\right)=x^{2} \) היא פונקציה קמורה בעוד \( g\left(x\right)=\sqrt{x} \) היא פונקציה קעורה. השמות מבלבלים: \( f\left(x\right)=x^{2} \) היא הפונקציה שיותר דומה לקערה (“פרבולה צוחקת” - זה יהיה יותר ברור אם נצייר את הפונקציה גם לערכים שליליים של \( x \)) ולמרות זאת המילה “קעורה” שמורה לפונקציה שנראית כמו קערה הפוכה. באנגלית המילה המתאימה ל”קמורה” היא Convex ול”קעורה” היא Concave ויש קצת יותר הגיון בהן, אבל לא ניכנס לכך כאן.

אז מה ההבדל האיכותי ביניהן ואיך אפשר לתאר אותו במדוייק? ההבדל הוא ש-\( x^{2} \) היא פונקציה שהמהירות שלה גדלה עם הזמן, בעוד ש-\( \sqrt{x} \) היא פונקציה שהמהירות שלה קטנה עם הזמן. תחשבו על שני רצים - אחד שמתחיל מהר והולך ומתעייף - זה \( \sqrt{x} \); ואחד שמתחיל לאט אבל לאט לאט הופך למהיר יותר ויותר - זה \( x^{2} \). הרץ הראשון יתחיל את המירוץ ביתרון, אבל מתישהו שני הרצים ייפגשו בדרך (בדיוק ב-\( x=1 \)) ומכאן ואילך הרץ השני יהיה בעל ההובלה. איפה טמון ההבדל המתמטי בין שני הרצים? הראשון הוא בעל מהירות התחלתית גבוהה אבל תאוצה שלילית (מהירותו קטנה), ואילו השני מתחיל עם מהירות התחלתית נמוכה אבל תאוצה חיובית (מהירותו גדלה). “תאוצה” היא, כזכור, הנגזרת השנייה של פונקציה (קצב השינוי של קצב השינוי שלה), ומכאן המסקנה: פונקציה היא קמורה בנקודה כלשהי (ליתר דיוק - בסביבה של נקודה כלשהי) אם הנגזרת השנייה שלה באותה נקודה היא חיובית, והיא קעורה אם הנגזרת השנייה שלילית.

יש לקמירות וקעירות גם הגדרה כללית יותר, שעובדת גם עבור פונקציות שהן לא בהכרח גזירות. ההגדרה שנתתי כרגע הייתה “נקודתית”, אבל בפועל קמירות וקעירות הן תכונות שבאות לידי ביטוי על פי התנהגות הפונקציה בתוך קטע שלם, לא רק בנקודה מבודדת. לכן בואו נביט על קטע \( \left[a,b\right] \). הוא מייצג פרק זמן מסויים, שבמהלכו שני הרצים שלנו, זה של \( f \) וזה של \( g \), עוברים את המרחק שבין \( f\left(a\right) \) ל-\( f\left(b\right) \). בואו נכניס לתמונה כעת רץ שלישי, \( h \), שגם הוא רץ מ-\( f\left(a\right) \) אל \( f\left(b\right) \) (כלומר, \( f\left(a\right)=g\left(a\right)=h\left(a\right) \) ו-\( f\left(b\right)=g\left(b\right)=h\left(b\right) \)) אבל הוא הרץ הכי יציב מבין שלושתם: את כל הדרך הוא עובר במהירות קבועה. אם נצייר את גרף הריצה שלו, הוא יהיה קו ישר ששיפועו \( \frac{h\left(b\right)-h\left(a\right)}{b-a} \).

הטענה שלי היא כזו: הרץ שהתחיל לאט ואט אט מגדיל את מהירותו, שתואר על ידי \( f \), תמיד מפגר מאחורי הרץ היציב \( h \) עד לנקודה שבה הם נפגשים. כלומר, לא ייתכן שיש רגע שבו \( f\left(x\right)>h\left(x\right) \) בכל הקטע \( \left[a,b\right] \). למה? חשבו על זה כך: בהתחלה מהירות הריצה של \( f \) קטנה מזו של \( h \) (כי אם היא הייתה גדולה מזו של \( h \) בהתחלה, והמהירות של \( f \) רק גדלה עוד ועוד עם הזמן, אז בנקודה \( b \) בהכרח \( f \) היה חייב להיות הרחק מעבר ל-\( h \)). כדי ש-\( f \) יצליח להשיג את \( h \) חייב להיות רגע שבו מהירותו של \( f \) עוברת את זו של \( h \), אבל מאותו רגע ואילך המהירות של \( f \) תהיה גדולה יותר תמיד מזו של \( h \), ולכן אחרי הפעם הראשונה שבה הוא יעקוף אותו, \( h \) לעולם לא ישיג אותו מחדש. נקודת המפגש הזו היא רק ב-\( b \) ולכן עד אז \( f \) חייב לפגר אחרי \( h \). מטיעונים סימטריים לגמרי מקבלים ש-\( g \) תמיד משיג את \( h \) עד לנקודה \( b \).

במילים אחרות, אם משרטטים את התנועה של \( f \), ואז בוחרים שתי נקודות על הגרף ומותחים ביניהן קו, אז הגרף של \( f \) בין אותן שתי נקודות יהיה תמיד מתחת לקו. בדומה עם \( g \) הגרף של הפונקציה יהיה תמיד מעל לקו. בנוסחה אומרים שפונקציה (כללית) \( f \) היא קמורה בקטע \( \left[a,b\right] \) אם לכל \( x\in\left[a,b\right] \) מתקיים \( f\left(x\right)\le\frac{f\left(b\right)-f\left(a\right)}{b-a} \). לפונקציות קעורות זה אותו דבר עם היפוך סימן אי השוויון.

בואו נמשיך עוד רגע עם האנלוגיה ל”הרץ שנע במהירות קבועה” כדי להבין עוד תופעה מבלבלת אחת שמתרחשת עם פונקציות קמורות וקעורות. בואו נניח ש-\( f \) היא קמורה - כזכור, זה אומר שהיא מייצגת “רץ שהמהירות שלו גדלה כל הזמן”. בואו ניקח נקודה כלשהי על גרף הפונקציה ונצייר את המשיק לאותה נקודה. מהו המשיק הזה? קו ישר, ששיפועו מייצג את המהירות הרגעית של \( f \) ברגע שמיוצג על ידי אותה נקודה. נקודות אחרות על הישר מייצגות את “איפה נמצא רץ שמהירותו קבועה ושווה למהירות בנקודת ההשקה ברגעים אחרים”. תדמיינו לעצמכם את הרץ של \( f \) מתרוצץ לו, ואז פתאום אנחנו מקפיאים את התמונה ומציירים לידו רץ חדש, כך שמהירות הרץ החדש שווה למהירות של \( f \) ברגע שהקפאנו. כעת אנו ממשיכים להריץ את הסרט, מה קורה? ברור ש-\( f \) יעבור את הרץ החדש, כי המהירות של \( f \) תהיה גדולה משל הרץ החדש (אמרנו ש-\( f \) מגדיל כל הזמן את מהירותו בעוד שהרץ החדש רץ במהירות קבועה).

אוקיי, עכשיו בואו נריץ את הסרט אחורה. האינטואיציה שלי אומרת שבמקרה הזה הרץ החדש צריך להשיג את \( f \) כי הוא מהיר יותר - ככל שמריצים את הסרט אחורה, המהירות של \( f \) נהיית קטנה יותר ויותר ביחס לזו של הרץ החדש. אבל האינטואיציה שלי פשוט שגויה - אם נריץ את הסרט אחורה, עדיין נראה את \( f \) משיג את הרץ החדש. למה? ובכן, כי אם הרץ החדש היה משיג את \( f \), והמהירות של הרץ החדש גדולה מזו של \( f \) עד לשלב שבו הם נפגשים (ואז היא שווה), איך בדיוק \( f \) יצליח להשיג אותו כך שהם ייפגשו?

הסרט המלא, אם כן, הוא זה: \( f \) רץ לו בניחותא ולאט לאט מגדיל את מהירותו. הרץ החדש רץ אליו במהירות קבועה ולאט לאט מצמצם את הפער… מתקרב… מתקרב… משיג אותו! אבל בשניה שאחר כך \( f \) כבר נהיה מהיר מדי והרץ החדש נשאר מאחור. כלומר, הרץ החדש אף פעם לא עובר את \( f \). ובמתמטיקה: המשיק ל-\( f \) בנקודה כלשהי, בתנאי ש-\( f \) קמורה בסביבת הנקודה הזו, נמצא כולו מתחת לגרף הפונקציה. שימו לב לבלבול - המשיק כולו מתחת, אבל אם מסתכלים על המיתר שמחבר שתי נקודות בסביבה של נקודת ההשקה, המיתר כולו מעל. אני מקווה שעם כל האינטואיציות שניסיתי לתת כאן העסק קצת פחות מבלבל.

עבור פונקציות קעורות כל הדיון עובד באותה מידה, כצפוי, ומקבלים שהמשיק בנקודה כלשהי הוא תמיד מעל לגרף הפונקציה.

טוב, סיימנו את הדיון הזה בפונקציות קמורות וקעורות - איך זה מתקשר לנקודות מינימום ומקסימום? בפשטות - בנקודת מינימום הפונקציה קמורה, ובנקודת מקסימום הפונקציה קעורה. זה נותן לנו קריטריון מיידי לזיהוי נקודות קיצון: אם הנגזרת הראשונה של הפונקציה היא אפס והשנייה היא חיובית, אז זוהי נקודת מינימום, אם הנגזרת הראשונה היא אפס והשניה שלילית, זוהי נקודת מקסימום, ואם גם הנגזרת השניה היא אפס אנחנו בצרות - הכל יכול לקרות.

שתי הדוגמאות הבסיסיות ל”הכל יכול לקרות” הן פשוטות מאוד: \( f\left(x\right)=x^{3} \) ו-\( f\left(x\right)=x^{4} \). בדוגמה של \( f\left(x\right)=x^{3} \) מה שקורה בנקודה \( x=0 \) הוא מה שקראתי לו “נקודת פיתול” - רגע לפני הפונקציה קעורה ורגע אחרי היא קמורה, וכל זה מבלי שהיא תפסיק לעלות מעלה. פורמלית זה מתבטא בכך שהנגזרת הראשונה בסביבות הנקודה הזו היא חיובית, והנגזרת השניה היא שלילית לפני 0 וחיובית אחרי 0. אם נחזור לדוגמת הרץ, מה שיש לנו פה הוא אדם שרץ ומאיט אט אט, נעצר לשבריר שניה ב-\( x=0 \), ואז מתחיל להאיץ מחדש. במשך כל הזמן הזה הוא מתקדם קדימה.

לעומת זאת ב-\( f\left(x\right)=x^{4} \) הנגזרת הראשונה היא אפס אבל שלילית לפני אפס וחיובית אחריו - מכאן שיש לנו פה נקודת מינימום - הרץ רץ “אחורה” עד ל-\( x=0 \) ואז התחיל לרוץ “קדימה”. אם היינו מנסים להבין זאת דרך הנגזרת השנייה היינו מסתבכים בצרות - הנגזרת השנייה היא גם כן אפס. וגם השלישית! רק הנגזרת הרביעית אינה אפס אלא מספר חיובי. זה מוביל אותנו לקריטריון המוזר הבא: אם הנגזרת הראשונה שאינה מתאפסת היא רציפה ומספרה זוגי, הנקודה היא היא נקודת מינימום או מקסימום (בהתאם לערכה של אותה נגזרת שלא התאפסה), ואם היא נגזרת (רציפה) שמספרה אי זוגי, הנקודה היא נקודת פיתול. תכף אסביר את הקריטריון הזה אבל עוד קודם לכן אעיר שזה לא סוף הסיפור - הנגזרת עשויה להיות לא מוגדרת בכלל, ולמרות זאת עדיין תהיה משמעות לשאלה אם הנקודה היא נקודת מינימום, מקסימום או פיתול (כל אלו הן תכונות “מקומיות” שלא דורשות נגזרת שניה אלא רק ראשונה). במקרים כאלו ייתכן שהנקודה לא תהיה לא נקודת מינימום, לא נקודת מקסימום וגם לא נקודת פיתול - דוגמה לפתולוגיה כזו היא הפונקציה \( f\left(x\right)=x^{2}\sin\left(\frac{1}{x}\right) \) שמוגדרת להיות 0 בנקודה 0, ואפשר להוכיח שהיא רציפה ואפילו גזירה (פעם אחת בלבד!) ב-\( x=0 \), וערך הנגזרת שם הוא 0, אבל אין שם לא נקודת קיצון וגם לא נקודת פיתול. בחיי היום יום בדרך כלל לא נתקלים בתופעות מטורללות שכאלו.

טוב, אז בואו נבין את הקריטריון שהצגתי לזיהוי נקודות קיצון אל מול נקודות פיתול. אני חושב שכדאי להתחיל כאן מהסוף - מהנגזרת הראשונה שאינה אפס - ולטפס מעלה. בואו נניח ש-\( f^{\left(n\right)}\left(x_{0}\right)=C \) כך ש-\( C>0 \) וה-\( n \) שהוא לכאורה חזקה של \( f \) מציין שזוהי הנגזרת ה-\( n \)-ית. כמו כן \( f^{\left(1\right)}\left(x_{0}\right)=\dots=f^{\left(n-1\right)}\left(x_{0}\right)=0 \). אז מה קורה כאן?

מכיוון ש-\( C>0 \) אז \( f^{\left(n\right)} \) (שהיא רציפה, הנחנו) היא חיובית בסביבה של \( x_{0} \). לכן \( f^{\left(n-1\right)} \) היא פונקציה עולה בסביבות \( x_{0} \). מכיוון שב-\( x_{0} \) היא אפס, הרי שלפני \( x_{0} \) היא שלילית, ואחרי כן היא חיובית. זה אומר, וכאן העסק מתחיל להיות מבלבל, ש-\( f^{\left(n-2\right)} \) היא שוב פונקציה שהיא תמיד חיובית. למה? כי לפני \( x_{0} \) היא ירדה, ובדיוק ב-\( x_{0} \) היא הייתה אפס, אז לפני כן היא הייתה חייבת להיות חיובית; ואחרי \( x_{0} \) היא שוב עולה מעלה. אבל זה אומר ש-\( f^{\left(n-2\right)} \) לא שונה עקרונית מ-\( f^{\left(n\right)} \), ולכן אפשר להמשיך את המשחק הזה עוד ועוד עד שמגיעים חזרה למעלה. נקבל בסופו של דבר ש-\( f^{\prime} \) היא או פונקציה שלילית-ואז-חיובית, ואז נקבל ש-\( x_{0} \) היא נקודת מינימום, או ש-\( f^{\prime} \) היא חיובית תמיד ואז \( f^{\prime\prime} \) היא הפונקציה שהיא שלילית-ואז-חיובית, כלומר \( x_{0} \) היא נקודת פיתול.

ואחרי כל המהומה הזו, איך אני פותר את השאלות שמהן התחלתי את הדיון? ובכן, האתגר הראשון היה למצוא איפה ל-\( \sin\left(2\theta\right) \) יש מקסימום בהינתן ש-\( \theta \) הוא בין 0 ל-90 מעלות. גזירה של הפונקציה מניבה את \( 2\cos\left(2\theta\right) \). קוסינוס מתאפס בתשעים מעלות, כך שהפונקציה הזו מתאפסת ב-45 מעלות. גזירה נוספת מניבה את \( -4\sin\left(2\theta\right) \), וכשמציבים 45 מעלות ל-\( \theta \)מקבלים שערך הנגזרת השנייה בנקודה ה”חשודה” הוא -4. נגזרת שנייה שלילית - נקודת מקסימום. סיימנו; 45 מעלות היא הזווית האופטימלית (ומי שמדגדג לו לצעוק עלי להשתמש כאן ברדיאנים - אל).

נעבור לדוגמת החתונות. שם, כזכור, המטרה הייתה למצוא את המינימום של הפונקציה \( f\left(x\right)=A+\left(b-c\left(x\right)\right)x \) כאשר \( c\left(x\right) \) היא פונקציה אחרת כלשהי (שהאופי שלה ישפיע מאוד על התוצאה). אם נגזור את \( f \) נקבל \( f^{\prime}\left(x\right)=\left(b-c\left(x\right)\right)-xc^{\prime}\left(x\right) \). מייד שמים לב למשהו מעניין - הפרמטר \( A \), שתיאר את ההוצאות הקבועות על חתונה, בכלל לא משתתף במשחק. מה שחשוב הוא רק המחיר למנה \( b \), והאופי של התשלומים שמשלמים האורחים, \( c \). פוטנציאל לנקודת קיצון יש במקום שבו הפונקציה מתאפסת, כלומר \( \left(b-c\left(x\right)\right)-xc^{\prime}\left(x\right)=0 \), כלומר \( b=c\left(x\right)+xc^{\prime}\left(x\right) \). אנו מעוניינים מראש רק בערכי \( x \) חיוביים כי הם מייצגים מספר חיובי - מספר האורחים שהוזמנו לחתונה. כעת אין מנוס אלא לבדוק דוגמאות קונקרטיות של \( c\left(x\right) \) ולראות מה קורה איתן.

דרך פשוטה לבנות פונקציה כזו היא להחליט מה יהיו חלק מהערכים שלה בנקודות מסויימות ואז לבצע אינטרפולציה: למצוא פונקציה פשוטה שמקבלת את הערכים באותן הנקודות. אני אבצע אינטרפולציה פשוטה במיוחד, שבהינתן שתי נקודות מחזירה את הקו הישר שעובר דרכן. בואו נניח שאם יש 0 אורחים אז התשלום הממוצע הוא \( 4b \), ואם יש 100 אורחים אז התשלום הממוצע הוא \( \frac{b}{2} \). זה תרגיל פשוט לראות שבמקרה הזה, \( c\left(x\right)=4b-\frac{7b}{200}x \). הנגזרת גם היא פשוטה: \( c^{\prime}\left(x\right)=-\frac{7b}{200} \), ולכן כדי שיתקיים השוויון שלעיל צריך להתקיים \( b=4b-\frac{7b}{200}x-\frac{7b}{200}x \), כלומר \( 3b=\frac{7b}{100}x \), כלומר \( x=\frac{300}{7} \) - בערך 42 אורחים. שימו לב שהתוצאה הסופית לא תלויה אפילו ב-\( b \): היא תלויה רק בפרמטרים שאני בחרתי (תשלום שבהתחלה הוא פי ארבע וכשיש 100 אורחים קופץ להיות חצי). אנחנו רואים, אם כן, שבסופו של דבר התשובה לשאלה “כמה אורחים כדאי להזמין” תלויה באופן כמעט בלעדי ביכולת שלנו להעריך כמה מהר יצנח התשלום שלהם, וזה כמובן נתון שלא ניתן להגיע אליו באופן מתמטי טהור נטו - הוא תלוי באלף ואחד גורמים וכנראה שאומדנים על בסיס סטטיסטיקות עבר הם הדרך הטובה ביותר להעריך אותו. אל תתנו לאנשים לסובב אתכם עם מספרים כשהם מנסים לטעון משהו על המספר האופטימלי של מוזמנים בחתונה שלכם!

עוד דוגמה קטנה לסיום: מהו המלבן בעל השטח הגדול ביותר ביחס להיקף שלו? אם אתם רוצים לבנות גדר לשטח ריבועי ולהשקיע כמה שפחות מאמץ וחומרים בבניה ושהשטח שאתם לוכדים יהיה מקסימלי, מה כדאי לכם לעשות? בואו נניח שיש לנו בסך הכל \( N \) מטרים של גדר שאפשר להשתמש בהם. אם נבנה מלבן שאורך צלעו האחת \( x \), אז אורך צלעו השניה יהיה חייב להיות \( \frac{N}{2}-x \) (בדקו זאת!) ולכן השטח יהיה \( f\left(x\right)=x\cdot\left(\frac{N}{2}-x\right)=\frac{N}{2}x-x^{2} \). הנגזרת היא \( f^{\prime}\left(x\right)=\frac{N}{2}-2x \) והיא מתאפסת כאשר \( 2x=\frac{N}{2} \), כלומר כאשר \( x=\frac{N}{4} \). קל לבדוק במצב כזה שזוהי אכן נקודת מקסימום (הנגזרת השנייה שלילית) ומכאן, באופן לחלוטין לא מפתיע, שריבוע היא הצורה הטובה ביותר.

אם כן, זה הרעיון הכללי של שימוש בנגזרות לפתרון בעיות קיצון. זה שימוש כה מיידי ופשוט, עד כי הוא נלמד גם בבית הספר - ולטעמי זו הזדמנות אחת לראות כבר בבית הספר יופי מתמטי. כאן מגיע מושג הנגזרת, שלכאורה מדבר על משהו לא קשור, וניתן להשתמש בו כדי לפתור בעיות מעניינות שהמילה “נגזרת” לא מוזכרת ולו ברמז בתיאור שלהן. למרות כל הזמן שחלף מאז שנתקלתי בשימוש הזה של נגזרות לראשונה, ולמרות שבבית הספר הוא הסתכם בגזירה שוב ושוב של המוני פונקציות מייגעות, אני עדיין מתלהב כשאני כותב עליו.