אנליזה מרוכבת - זה הרגע לגלות את הנפשות הפועלות

אחרי שמציגים את המושגים הבסיסיים שקשורים למספרים מרוכבים, יש שתי דרכים להמשיך ולפתח את האנליזה המרוכבת. דרך אחת היא לקחת את ההגדרות המוכרות מחשבון דיפרנציאלי ואינטגרלי של מספרים ממשיים, להכליל אותן ולהתחיל להוכיח משפטים; דרך אחרת היא קודם כל להציג כמה מהפונקציות העיקריות שבהן אנו מתענייינים באנליזה המרוכבת ולהסביר קצת על האופן שבו נהוג לתאר אותן בצורה גרפית. אני מעדיף לנקוט בגישה השניה - וכמובן, לתאר דברים בצורה שהיא יחסית לא פורמלית.

מאינפי אנחנו מכירים כמה פונקציות בסיסיות וחשובות - פולינומים, הפונקציה האקספוננציאלית \( e^{x} \), הפונקציות הטריגונומטריות \( \sin x,\cos x \), פונקציית השורש \( \sqrt{x} \) ופונקציית הלוגריתם \( \ln x \). אלו הפונקציות שיעניין אותי בשלב ראשון לתאר איך מכלילים אותן למספרים המרוכבים.

כרגיל, הכי קל לעבוד עם פולינומים. יש לנו פעולות חיבור וכפל במספרים המרוכבים, ופולינום הוא פונקציה שלוקחת מספר מרוכב כלשהו, כופלת אותו בעצמו מספר כלשהו של פעמים, כופלת את התוצאה בעוד מספר מרוכב קבוע כלשהו (“מקדם”) ואז מחברת כמה וכמה כפולות כאלו.

פורמלית זו כל פונקציה מהצורה \( p\left(z\right)=a_{n}z^{n}+a_{n-1}z^{n-1}+\dots+a_{1}z+a_{0} \) כאשר \( a_{0},\dots,a_{n}\in\mathbb{C} \) ו-\( a_{n}\ne0 \). המעלה של הפולינום היא \( n \), ל-\( a_{n} \) קוראים המקדם המוביל של הפולינום ול-\( a_{0} \) קוראים המקדם החופשי. וזה בערך כל מה שאני רוצה לומר על פולינומים כרגע.

הפונקציה הבאה ברמת הפשטות שלה היא הפונקציה האקספוננציאלית. הייתי שמח לתת לה הגדרה שאני מרוצה ממנה, אבל בשלב הזה של הדיון אין לנו עדיין יכולת לעשות את זה - הגדרה “נכונה” של הפונקציה מערבת טורי חזקות, ועוד לא דיברנו על התורה של טורי חזקות במספרים המרוכבים (אם כי אגלה כבר מראש שזה אותו הדבר בדיוק כמו במספרים הממשיים). לכן אני נוקט בהגדרה שתיראה מוזרה, אולי אפילו כמו הונאה: אני מגדיר \( e^{a+ib}=e^{a}\left(\cos b+i\sin b\right) \) (כאשר \( e^{a} \) זו הפונקציה האקספוננציאלית הממשית, הרי \( a \) הוא מספר ממשי). במילים אחרות, אני משתמש בנוסחת אוילר שהזכרתי בפוסט הקודם בתור הגדרה. קשה להגיד שעשיתי משהו לא חוקי - מותר לי להגדיר פונקציה בכל אופן שאני מוצא לנכון כל עוד מה שאני מגדיר אכן מקיים את הדרישות מפונקציה (שלכל קלט אפשרי יהיה קיים פלט יחיד), אבל לא ברור למה ההגדרה שלי היא “נכונה”.

השלב הבא עשוי להיות מעליב עוד יותר עבור הקורא שלא אוהב להרגיש שמרמים אותו. אני רוצה להגדיר פונקציות טריגונומטריות מרוכבות, כלומר \( \sin z,\cos z \). איך אעשה את זה? ובכן, קודם כל אני שם לב לכך שהפונקציות הטריגונומטריות הממשיות ניתנות להסקה מתוך נוסחת אוילר, באופן הבא:

אם \( e^{i\theta}=\cos\theta+i\sin\theta \) אז \( e^{-i\theta}=\cos\theta-i\sin\theta \) (זה נובע מכך ש-\( \cos\left(-\theta\right)=\cos\theta \) ואילו \( \sin\left(-\theta\right)=-\sin\theta \) - במילים, \( \cos \) היא פונקציה זוגית ואילו \( \sin \) היא פונקציה אי זוגית). לכן \( e^{i\theta}+e^{-i\theta}=2\cos\theta \), כלומר \( \cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2} \). בדומה, \( \sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i} \). אם כן, למה לא להגדיר את הפונקציות הטריגונומטריות בצורה דומה, רק עבור מספר מרוכב כלשהו? נגדיר:

\( \sin z=\frac{e^{iz}-e^{-iz}}{2i} \)

\( \cos z=\frac{e^{iz}+e^{-iz}}{2} \)

נראה קצת עקום - אנחנו מגדירים סינוס וקוסינוס מרוכבים על ידי אקספוננט מרוכב שמוגדר על ידי סינוס וקוסינוס ממשיים. מצד שני, זה גם קצת משעשע.

כעת אפשר לדבר על פונקציות השורש והלוגריתם. הפונקציות הללו הן הופכיות של פונקציות שכבר הגדרנו: שורש הוא ההופכי של \( z^{2} \), ולוגריתם הוא ההופכי של \( e^{z} \). צריך להוכיח שהופכי כזה בכלל מוגדר, אבל נעזוב את זה לבינתיים ונתמקד בבעיה המעניינת הרבה יותר שיש לנו: יש כמה פונקציות הופכיות שונות. זה המושג של ענפים שהזכרתי בפוסט הקודם. לפני שניכנס לנושא הזה, בואו ננסה לחשוב לרגע על הפונקציות שכבר ראינו באופן גאומטרי יותר - ובד בבד לדון בשאלה איך אפשר לצייר אותן.

איך מציירים פונקציות ממשיות כולנו יודעים. הנה למשל הגרף של \( f\left(x\right)=x^{2} \):

 

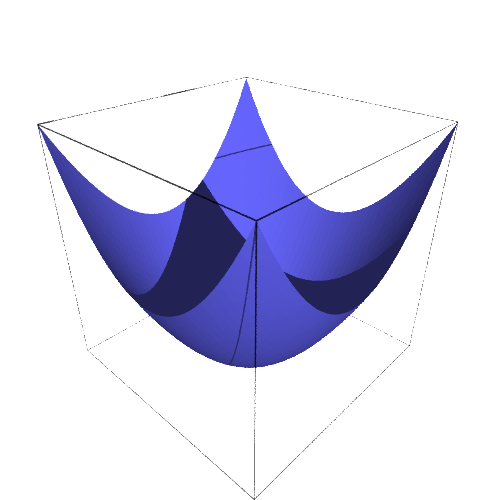
הרעיון בגרף הוא פשוט: ציר אחד מתאר את ערכי ה-\( x \) שהפונקציה מקבלת, והציר השני מתאר את ערכי הפלטים הפלטים שהפונקציה יכולה לקבל. אנחנו מסמנים כל נקודה מהצורה \( \left(x,f\left(x\right)\right) \), וקיבלנו ייצוג ויזואלי יפה של הפונקציה. אפשר לעשות תעלול דומה גם עבור פונקציות שמקבלות שני מספרים ממשיים ומחזירות מספר ממשי בודד - במקרה הזה הגרף ייראה כמו משטח, שהערך של הפונקציה קובע את הגובה שלו. הנה המשטח שמתאים ל-\( f\left(x,y\right)=x^{2}+y^{2} \):

פורמלית, הגרף הזה הוא אוסף כל השלשות \( \left(x,y,f\left(x,y\right)\right) \) במרחב, כלומר תת-קבוצה של \( \mathbb{R}^{3} \).

כל זה טוב ויפה, אבל מה עושים עם פונקציות מרוכבות? כל מספר מרוכב מתואר על ידי זוג של מספרים ממשיים, כך שהגרף של פונקציה מרוכבת יהיה אוסף של נקודות שנראות ככה: \( \left(a+bi,\mbox{Re}f\left(a+bi\right)+\mbox{Im}f\left(a+bi\right)i\right) \), או כשננסה לצייר אותן בתוך מרחב ממשי כלשהו, רביעיות של נקודות שנראות כך: \( \left(a,b,\mbox{Re}f\left(a+bi\right),\mbox{Im}f\left(a+bi\right)\right) \). הבעיה היא שאנחנו לא יודעים לצייר דברים ארבע-ממדיים בצורה נוחה במיוחד. זה לא אומר שאי אפשר לעשות את זה - אפשר להשתמש, למשל, בצבעים כדי להוסיף מימד נוסף לתמונה וגם עושים את זה - אבל אני לא הכי אוהב את הגישה הזו. יש גישה אחרת לכל העניין, שבמובנים מסויימים עוזרת הרבה יותר להבין את הפונקציות - להסתכל לא על כל הפונקציה בבת אחת, אלא לראות מה היא עושה לתת-קבוצות “נחמדות” של \( \mathbb{R}^{2} \). בשיטה הזו מציירים גרף אחד שהוא תת-קבוצה של המישור המרוכב לפני הפעלת הפונקציה, וגרף אחר שהוא התמונה של אותה תת-קבוצה אחרי הפעלת הפונקציה. לעתים קרובות גם מוסיפים חצים במרווחים שווים כדי לתת תחושה של כמה הפונקציה “מנפחת” או “מכווצת”. הדרך הטובה ביותר להסביר את זה היא לתת דוגמה:

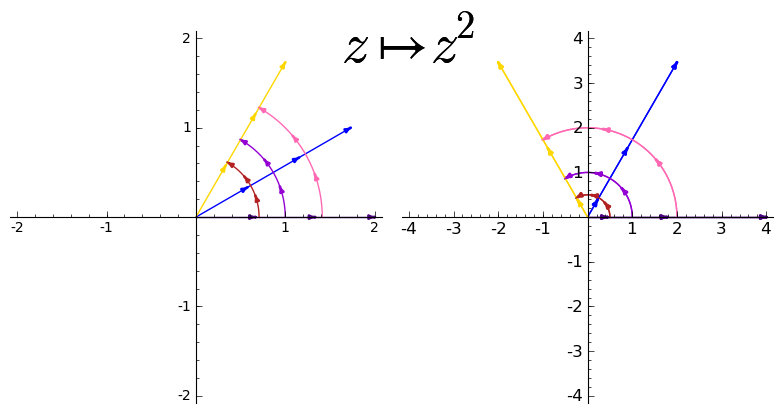
מה הולך כאן בכלל? ובכן, ראשית אני מתנצל אם האיורים נראים חובבניים - הם באמת כאלו! לא הצלחתי למצוא שום כלי שייצר בדיוק את מה שרציתי, אז כתבתי סקריפט ב-Sage (שאפשר לראות כאן) שיעשה את זה בשבילי. אני מקווה שהאיורים מספיק ברורים כדי להבין את הנקודות שאני רוצה להמחיש.

ובכן, האיור מורכב משני מישורים - השמאלי הוא המקור והימני הוא התמונה. במישור השמאלי אנחנו רואים כל מני עקומות במישור - במקרה שלנו אלו שלושה קווים ישרים ושלוש קשתות. כל הישרים הם מאורך 2, ויוצרים זוויות של \( 0^{\circ},30^{\circ},60^{\circ} \) עם הכיוון החיובי של ציר \( x \). הקשתות הן כולן מהזווית \( 0^{\circ} \) ועד \( 60^{\circ} \), והן נבדלות ברדיוס המעגלים שלהן (כל קשת היא חלק ממעגל שמרכזו בראשית הצירים): הרדיוסים הם \( \sqrt{\frac{1}{2}},1,\sqrt{2} \). למה רדיוסים כאלו? כדי שיצא נחמד אחר כך.

עכשיו, המישור הימני ממחיש מה קורה לעקומים הללו אחרי שמפעילים עליהם את הפונקציה \( f\left(z\right)=z^{2} \). בואו ניקח לדוגמה את הקטע שהזווית שלו עם ציר \( x \) היא \( 60^{\circ} \), כלומר \( \frac{\pi}{3} \) רדיאנים: המשוואה של עקום כזה היא \( z\left(t\right)=te^{i\frac{\pi}{3}} \) כאשר \( 0\le t\le2 \) (“עקום” בהקשר של המרחב הממשי הוא פונקציה \( f:\mathbb{R}\to\mathbb{R}^{2} \) שנהוג לסמן בתור \( f\left(t\right)=\left(x\left(t\right),y\left(t\right)\right) \); כאשר \( f\left(t\right) \) מחזיר מספר מרוכב הוא מכיל בו זמנית את המידע על קואורדינטת ה-\( x \) ועל קואורדינטת ה-\( y \)). על כן, אחרי שנפעיל את \( f\left(z\right)=z^{2} \) על העקום, נקבל את העקום החדש \( \left(te^{i\frac{\pi}{3}}\right)^{2}=t^{2}e^{i\frac{2\pi}{3}} \). מה קרה? האורך של העקום הועלה בריבוע, בעוד שהזווית של העקום הוכפלה פי 2. ואכן, בציור די קל לראות שהאורך החדש של הקטע הוא פחות או יותר 4, ושהזווית שלו גדלה מספיק כדי להעביר אותו לרביע השני (מדידה מדוייקת תראה שהיא אכן \( 120^{\circ} \)). באופן דומה אפשר להבין את מה שקרה לשני הקטעים האחרים, כשהמעניין מביניהם הוא זה שקשה לראות, שפשוט נח על ציר \( x \) ולא זז משם גם אחרי הפעלת הפונקציה (כי זווית 0, כשכופלים אותה ב-2, נותרת 0). שימו לב גם לחצים - אני מצייר חץ בכל פעם שהפרמטר \( t \) עובר עוד רבע מהתחום הכולל שלו, ולכן בגרף של המקור הם במרווחים שווים; בגרף של התמונה המרווחים כבר אינם שווים - מדוע?

עכשיו, מה קורה לקשתות? אותו הדבר! הרדיוס של הקשת מועלה בריבוע, בעוד שאורך הקשת גדל פי 2. זה אומר, בפרט, שמעגל שלם של \( 360^{\circ} \) הולך לעבור לשני מעגלים שמכסים האחד את השני; עוד נחזור לזה. הקשתות שלי נבחרו כך שאחת מהן תגדל ברדיוסה (משורש 2 ל-2), השניה לא תשתנה (מ-1 ל-1) ואילו השלישית תקטן (מהשורש של חצי - שגדול מחצי - אל חצי).

אני חושב ששילוב שתי דרכי ההתבוננות הללו - מה העלאה בריבוע עושה לקטעים שיוצאים מהראשית, ומה היא עושה לקשתות שמקיפות את הראשית - עוזרות לתת תחושה טובה מאוד של איך \( z^{2} \) מתנהגת. ואם הבנו את \( z^{2} \), אז בעצם \( z^{n} \) לכל \( n \) טבעי זה אותו רעיון. עכשיו אפשר לעבור לפונקציה יותר מתוחכמת.

הפונקציה המתבקשת היא אקספוננט: אנחנו מתארים ממילא מספרים מרוכבים עם אקספוננט, אז למה לא לקחת את זה לשלב הבא?

מה הולך כאן? יש לנו שתי קבוצות של ישרים - אופקיים ואנכיים. הישרים האופקיים עוברים לישרים שיוצאים מהראשית בזווית כלשהי (“קרניים”); הישרים האנכיים הופכים למעגלים. למה זה? פשוט למדי. המשוואה של ישר אופקי היא \( z\left(t\right)=t+bi \) כאשר \( b \) קבוע ומתאר את הגובה של הישר ביחס לציר \( x \) (גובה שיכול להיות גם שלילי, כמובן). אחרי הפעלת אקספוננט, נקבל \( e^{t+bi}=e^{t}\cdot e^{bi} \). כלומר, ישר שנמצא בזווית \( b \) עם הכיוון החיובי של ציר \( x \). נסו רגע לדמיין בעיני רוחכם אנימציה (צר לי, אני לא מוכשר מספיק כדי לתכנת משהו אינטראקטיבי) - קחו ישר אופקי והרימו/הורידו אותו, ודמיינו את התמונה שלו מסתובבת בהתאם.

נעבור לישרים אנכיים, כלומר מהצורה \( a+ti \). כאן הם יעברו ל-\( e^{a}\cdot e^{ti} \), כלומר למעגל בעל רדיוס קבוע (\( e^{a} \)) שמסתובב כל הזמן (בכל פעם שבה \( t \) עובר על פני אורך של \( 2\pi \) מהישר הוא משלים עוד סיבוב; בכוונה ציירתי קטעים שאורכם \( 2\pi \). דמיינו מה קורה כשמזיזים את הישר האנכי ימינה ושמאלה - כשמזיזים ימינה המעגל “מתנפח”, וכשמזיזים שמאלה הוא “מתכווץ” עד אינסוף (ככל שהישר יותר שמאלי כך המעגל בעל רדיוס קטן יותר; שימו לב שבראשית הצירים הרדיוס יהיה 1 ואחר כך הוא ימשיך לקטון - אין פה סימטריה ביחס לצירים).

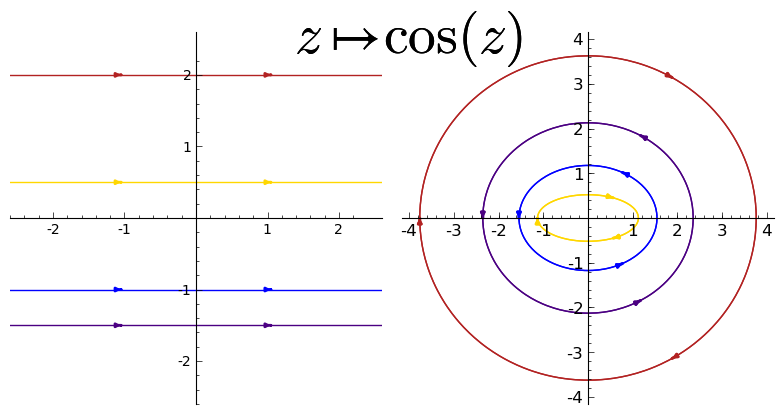
עכשיו בואו נעבור לקוסינוס, וננסה לנחש קודם כל מה יקרה. קוסינוס הוא \( \frac{e^{iz}+e^{-iz}}{2} \). אפשר להתעלם מהחלוקה ב-2 שכנראה לא תהיה מהותית להבנת הגיאומטריה פה - נסתכל על \( e^{iz}-e^{-iz} \). איך המכפלה ב-\( i \) במכנה משפיעה? היא מחליפה את תפקידי החלק הממשי והמדומה. בואו נסתכל שניה על \( e^{iz} \) לבדה - אם נציב \( z=a+bi \) נקבל \( e^{-b+ai}=e^{-b}e^{ai} \), כלומר כאן הסיבוב דווקא נקבל על ידי \( a \) ואילו \( b \) שולט על הרדיוס, אבל באופן הפוך למה שקרה באקספוננט - כאן ככל ש-\( b \) גדול יותר (קחו ישר אופקי ותרימו אותו מעלה מעלה) כך הרדיוס יהיה קטן יותר.

אבל, זה רק חלק מהסיפור! יש לנו גם את \( e^{-iz} \) במשחק, והוא יהפוך ל-\( e^{b-ai}=e^{b}e^{-ai} \). ההבדל בינו ובין \( e^{iz} \) הוא בכך שכיוון הסיבוב מתהפך (בגלל ש-\( a \) הוכפל במינוס 1), ושככל ש-\( b \) גדול יותר כך הערך של \( e^{iz} \) גדול יותר. במובן מסויים \( e^{iz} \) ו-\( e^{-iz} \) משלימים אחד את השני - כל אחד מהם הופך ליותר ויותר דומיננטי עבור ישרים אופקיים שהולכים ומתרחקים מראשית הצירים. לכן די ברור שעבור ערכים גדולים מאוד או קטנים מאוד של \( b \) נקבל משהו שנראה כמו מעגל. אבל עבור ערכים קטנים? האם אתם יכולים לנחש מה נראה?

ובכן, אולי אתם יכולים, אני בטח שלא יכול. במקום זאת, בואו נחשב דברים בפועל עם נוסחת אוילר: \( e^{-b}e^{ai}=e^{-b}\cos a+ie^{-b}\sin a \), ובדומה \( e^{b}e^{-ai}=e^{b}\cos a-ie^{b}\sin a \). לכן, אם נסכום את שניהם, נחשוב על \( a \) בתור פרמטר \( t \) ונסתכל על העקום שנקבל, נראה שקיבלנו עקום מהצורה \( \left(\frac{e^{-b}+e^{b}}{2}\cos t,\frac{e^{-b}-e^{b}}{2}\sin t\right) \). את הנוסחה הזו אולי אתם מכירים בתור ההצגה הפרמטרית של אליפסה. ואכן, אם נסתכל על מה שנקבל עבור ערכי \( b \) קטנים נראה בבירור אליפסה; כמובן, גם עבור ערכי \( b \) גדולים (בערכם המוחלט) אנחנו מקבלים אליפסה ולא מעגל, אבל אליפסה שנראית מאוד מאוד דומה למעגל.

והנה התמונה:

(שימו לב - והסבירו לעצמכם - לכיווני החצים על האליפסות השונות).

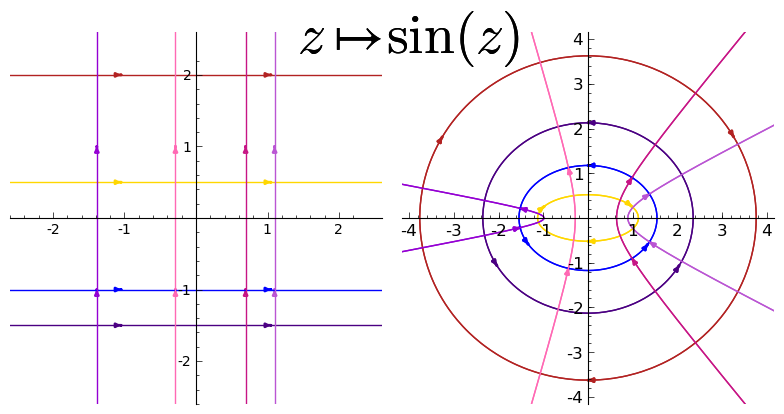
כל זה - רק עבור ישרים אופקיים, שבהם \( a \) משתנה ו-\( b \) קבוע. מה קורה עבור ישרים אנכיים, מהצורה \( a+ti \)? טוב, כאן קורה משהו מוזר מאוד שיש סיכוי שלא יהיה מוכר ללא מעט קוראים, כי בבית הספר בכלל לא נתקלים במשהו כזה. אנחנו נקבל עקום מהצורה \( \left(\frac{e^{t}+e^{-t}}{2}\cos a,\frac{e^{t}-e^{-t}}{2}\sin a\right) \) (קצת הפכתי את הסימן של \( t \) כדי שיתאים לסטנדרט שאני בא לתאר) אם עכשיו אסמן \( \alpha=\cos a \) ו-\( \beta=\sin a \) אני אוכל לכתוב את העקום גם בצורה שונה: \( \left(\alpha\cosh t,\beta\sinh t\right) \), כאשר \( \cosh \) ו-\( \sinh \) הן פונקציות ממשיות שידועות בתור פונקציות היפרבוליות, וראוי להקדיש להן פוסט שלם משל עצמן - מה שלא אעשה כעת. רק אעיר שהן מוגדרות בתור \( \cosh x=\frac{e^{x}+e^{-x}}{2} \) ו-\( \sinh x=\frac{e^{x}-e^{-x}}{2} \) (הדמיון בין הגדרה זו להגדרה של סינוס וקוסינוס מרוכבים הוא כמובן לא מקרי, וגם לא הבחירה בשמות “קוסינוס היפרבולי” ו”סינוס היפרבולי” עבור הפונקציות). כפי שהעקום שמתואר על ידי הפרמטריזציה \( \left(\alpha\cos t,\beta\sin t\right) \) מתאר אליפסה, כך העקום שמתואר על ידי הפרמטריזציה \( \left(\alpha\cosh t,\beta\sinh t\right) \) מתאר היפרבולה, ומכאן ה”היפרבולי” בשם הפונקציות. לכן לא מפתיע כל כך - עבור מי שיודע איך היפרבולה אמורה להיראות - לראות את התמונה הבאה:

אפשר לנחש בשלב הזה שתמונה של סינוס תהיה דומה, אולי עם החלפת תפקידים של ישרים אנכיים ואופקיים, אבל כאן מצפה לנו עוד הפתעה קטנה - החלק השני של ההיפרבולה:

מאיפה זה הגיע? ובכן, אפשר לבצע את החישוב המפורש או לנקוט בדרכי קיצור, אבל בסופו של דבר זה נובע מהתכונה הישנה לפיה קוסינוס היא פונקציה זוגית ואילו סינוס היא פונקציה אי זוגית.

לא סיימנו לטפל בפונקציות כי טרם הגענו לחלק המעניין באמת - הגדרת פונקציות שהן הופכיות של פונקציות אחרות (שורש, לוגריתם). עם זאת, נחכה עם זה קצת, ובפוסט הבא סוף סוף נלכלך את הידיים עם קצת אנליזה. אני מקווה שנהנתם בינתיים - הגרפים שהצגתי מבהירים, לטעמי, עד כמה הפונקציות המוכרות לנו הופכות למעניינות כשמסתכלים עליהן במישור המרוכב, והאופן שבו פתאום נכנסות לתמונה צורות גאומטריות מבית הספר כמו אליפסות והיפרבולות הוא בכלל בונוס משמעותי.