טורי פורייה - מה זה בכלל?
מתמטיקאים אוהבים לפרק דברים לגורמים. כל מספר טבעי קל יותר להבין אם מפרקים אותו למכפלה של ראשוניים. גם עם פונקציות ממשיות זה עובד כך - אחד מהדברים האהובים על מתמטיקאים הוא לקחת פונקציה ממשית \( f\left(x\right) \) ולכתוב אותה בתור טור חזקות: \( f\left(x\right)=\sum_{n=0}^{\infty}a_{n}x^{n} \). בצורה הזו הפונקציה נכתבת כסכום אינסופי של פונקציות פשוטות במיוחד - \( x^{n} \) - כשלכל פונקציה פשוטה שכזו יש מקדם, \( a_{n} \), שהוא מספר ממשי שמלמד אותנו עד כמה הרכיב \( x^{n} \) משתתף בסכום שמהווה את \( f\left(x\right) \). אם אנחנו יודעים ייצוג של \( f\left(x\right) \) כטור חזקות קל מאוד לעשות איתה דברים מסויימים - למשל, כדי לגזור אותה די לנו לגזור את הטור “איבר איבר”, ואת זה קל מאוד לעשות כי אנחנו יודעים איך גוזרים פונקציה פשוטה כמו \( x^{n} \) - מקבלים \( f^{\prime}\left(x\right)=\sum_{n=1}^{\infty}na_{n}x^{n-1} \). באופן דומה גם אינטגרל לפונקציה ניתן לתיאור על ידי ביצוע אינטגרציה לטור “איבר איבר”. אמנם, לא כל פונקציה אפשר לתאר כטור שכזה, ולא תמיד קל למצוא את הטור, אבל זו המחשה פשוטה ונאה לכוח שבפירוק שכזה.
הטור שתיארתי כרגע נקרא טור טיילור, והוא לחלוטין לא האופן היחיד שבו ניתן לפרק פונקציה לגורמים. הדרך שאני רוצה לתאר כעת, שהומצאה בידי פורייה, מפרקת את הפונקציה לרכיבים שמצד אחד אינם פשוטים כמו \( x^{n} \), ומצד שני הם מעניינים יותר במובן מסויים - פונקציות מחזוריות; ספציפית, סינוסים וקוסינוסים. הפירוק הזה נותן לנו דרך התבוננות חדשה על פונקציות, שלעתים קרובות מאוד נותנת לנו תובנות חדשות עליהן; ללא צל של ספק, הפירוק הזה של פורייה הוא אחד מהרעיונות הפורים והחשובים ביותר במתמטיקה. בפוסט הזה (ובהמשכיו) אני רוצה לתת תיאור על קצה המזלג שלו. מראש אזהיר שאני לא מראה שימושים כאן, למרות שכאמור - יש אינספור שימושים. אחת מהסיבות שבגללן אני כותב את הפוסט הזה היא כדי שאוכל בעתיד להציג תוצאות שעושות שימוש בסוג כלשהו של אנליזת פורייה ואוכל להפנות לכאן בשביל הבסיס.
עוד אזהרה היא שהפוסט הזה מניח ידע קודם במתמטיקה, ספציפית ידע כלשהו באלגברה לינארית ובחשבון אינפיניטסימלי וטיפה על מרחבי הילברט. זה מצער אותי מאוד, אבל טורי פורייה הם פשוט לא נושא שאפשר להציג בצורה טובה, לטעמי, בלי להיכנס לפרטים הטכניים שלהם (שדורשים אינפי) ובלי להציג קצת מהתמונה הגדולה שסביבם (שדורשת אלגברה).
דבר אחד שצריך להבין כשמדברים על אנליזת פורייה הוא שמדובר על תחום רחב, עם המון גרסאות שונות שעמוק בפנים הן כולן נובעות מאותו בסיס משותף. אם שמעתם על פורייה יש סיכוי לא רע ששמעתם לפחות על שלושה דברים: טורי פורייה, התמרת פורייה והתמרת פורייה הבדידה. אלו שלושה דברים שונים, אבל עם קשרים מאוד חזקים ביניהם. אני הולך בפוסטים הקרובים לדבר על כולם ולהציג את הקשרים הללו, אבל לפחות בינתיים אני לא הולך עמוק מכך לתיאוריה הכללית יותר - אז קחו בחשבון שאנחנו רק מגרדים פה את פני השטח. בפוסט הזה אני הולך לדבר רק על טורי פורייה, אז לעת עתה נשכח מכך שאמורים להיות עוד סוגים.
נתחיל מהכוכבים שלנו - הפונקציות הטריגונומטריות, סינוס וקוסינוס. כבר הצגתי אותן פעם בבלוג בצורה שאני מחשיב לצורה ה”נכונה” להסתכל עליהן - בתור הפתרונות הבסיסיים של משוואה דיפרנציאלית חשובה מסויימת. אולי התכונה הבולטת ביותר של שתי הפונקציות הללו היא שהן מחזוריות, עם מחזור של \( 2\pi \); באופן כללי, פונקציה \( f \) היא מחזורית עם מחזור \( a \) אם \( f\left(x\right)=f\left(x+a\right) \). כעת נשאלת השאלה - אילו פונקציות מחזוריות אפשר לכתוב בתור צירוף לינארי כזה של סינוסים וקוסינוסים?
התשובה - וזו תשובה די מפתיעה - היא שהרבה.
אני הולך לדבר רק על פונקציות עם מחזור של \( 2\pi \), אבל זה לא באמת מגביל אותי - אפשר את מה שאני עושה כאן להכליל לפונקציות עם מחזורים שונים עם תיקונים קטנים בלבד. כמו כן, אם \( f:\mathbb{R}\to\mathbb{R} \) היא פונקציה מחזורית, אין לי צורך אמיתי להתעסק עם כל \( \mathbb{R} \) בתור התחום שלה - מספיק לי להבין את הפונקציה הזו בתוך קטע מאורך \( 2\pi \) כדי שאבין אותה בכל הישר הממשי (כי ההתנהגות שלה מחוץ לקטע הזה זהה להתנהגות שלה בתוך הקטע). לכן אני הולך לדבר מעכשיו על פונקציות כלשהן \( f:\left[-\pi,\pi\right]\to\mathbb{R} \), והשאלה שלי היא מתי אפשר להציג אותן בתור צירוף לינארי של סינוסים וקוסינוסים. כעת, מכיוון שאני מדבר על מרחב של פונקציות ממשיות, הרי שזה לא מרחב סוף-ממדי; וכבר דיברתי בבלוג על כך שזה עושה לנו בעיות אם אנחנו רוצים להסתפק בצירופים לינאריים סופיים ואנחנו מעדיפים לדבר על צירופים לינארים אינסופיים. מה יהיו אברי הבסיס שלי? סינוסים וקוסינוסים, אבל לא רק \( \sin x \) ו-\( \cos x \) אלא \( \sin nx \) ו-\( \cos nx \) לכל \( n \) טבעי. בלשון של מרחבי הילברט, אני רוצה לטעון שקבוצת הפונקציות הללו היא מערכת אורתונורמלית שלמה במרחב של פונקציות שהן “נחמדות מספיק”. בשביל להשתמש במושג כמו “אורתונורמליות” אני צריך להגדיר מכפלה פנימית, אז הנה היא:
\( \left\langle f,g\right\rangle =\int_{-\pi}^{\pi}f\left(x\right)g\left(x\right)dx \)
והמרחב שלי יכלול את כל הפונקציות שההגדרה הזו “עובדת” בשבילן - כלומר, כל הפונקציות שמקיימות \( \int_{-\pi}^{\pi}f^{2}\left(x\right)dx<\infty \).
כדי לפשט חישובים בהמשך, בואו ניזכר בכמה תכונות של סינוסים וקוסינוסים. ראשית כל, סינוס הוא מה שנקרא פונקציה אי זוגית, ואילו קוסינוס הוא מה שנקרא פונקציה זוגית. פונקציה אי זוגית היא פונקציה שמקיימת \( f\left(-x\right)=-f\left(x\right) \) ופונקציה זוגית היא פונקציה שמקיימת \( f\left(-x\right)=f\left(x\right) \). לפונקציות אי זוגיות שאינטגרביליות בתחום מסויים שהוא סימטרי סביב הראשית יש את התכונה הנחמדה שהאיטגרל שלהן הוא 0, כי
\( \int_{-a}^{a}f\left(x\right)dx=\int_{0}^{a}f\left(x\right)dx+\int_{-a}^{0}f\left(x\right)dx=\int_{0}^{a}f\left(x\right)dx+\int_{0}^{a}f\left(-x\right)dx= \)
\( =\int_{0}^{a}f\left(x\right)dx-\int_{0}^{a}f\left(x\right)dx=0 \)
מה שאומר שבפרט, במקרה שלנו, \( \int_{-\pi}^{\pi}\sin nxdx=0 \). עכשיו, קוסינוס זה סיפור די דומה אבל לא זהה. בגלל שהוא פונקציה זוגית, אז \( \int_{-\pi}^{\pi}\cos nxdx=2\int_{0}^{\pi}\cos nxdx \). בואו נזכור שקוסינוס הוא בסך הכל סינוס שנתנו לו יתרון של \( \frac{\pi}{2} \) במירוץ, כלומר \( \cos x=\sin\left(x+\frac{\pi}{2}\right) \) ובאופן כללי יותר, \( \cos nx=\sin\left(nx+\frac{\pi}{2}\right) \). זה אומר שקוסינוס הוא פונקציה אי-זוגית אם מסתכלים עליו סביב הנקודה \( \frac{\pi}{2} \) ולא סביב 0, ולכן \( \int_{0}^{\pi}\cos nxdx=0 \).
הדבר האחרון שצריך לזכור הוא את הזהויות הטריגונומטריות הנוגעות למכפלה של סינוסים וקוסינוסים. הנה הן:
\( \sin x\sin y=\frac{\cos\left(x-y\right)-\cos\left(x+y\right)}{2} \).
\( \cos x\cos y=\frac{\cos\left(x-y\right)+\cos\left(x+y\right)}{2} \).
\( \sin x\cos y=\frac{\sin\left(x+y\right)+\sin\left(x-y\right)}{2} \).
כל הזהויות הללו עושות באופן כללי את אותו הדבר - הופכות מכפלה של שני סינוסים או שני קוסינוסים לסכום-עם-מקדמים של סינוסים וקוסינוסים בודדים (שלא מוכפלים באף אחד).
עכשיו קל לראות שכל הסינוסים והקוסינוסים הללו אורתוגונליים אחד לשני. \( \int_{-\pi}^{\pi}f\left(x\right)g\left(x\right)dx \) כאשר \( f,g \) הם סינוסים או קוסינוסים הולך להפוך לסכום אינטגרלים של כמה סינוסים וקוסינוסים וכבר ראינו שכל האינטגרלים הללו יצאו 0. אתם מוזמנים לנסות כמה מקרים באופן מפורש כדי להשתכנע. יש רק מקרה אחד שבו זה יכול להשתבש - כאשר אנחנו כופלים פונקציה בעצמה. במקרה הזה, נקבל בנוסחאות \( \cos\left(x-x\right)=\cos0=1 \) ולכן נקבל אינטגרל שונה מאפס. למשל:
\( \left\langle \sin nx,\sin nx\right\rangle =\int_{-\pi}^{\pi}\sin nx\sin nxdx=\frac{1}{2}\int_{-\pi}^{\pi}\left(1-\cos nx\right)=\frac{1}{2}\cdot2\pi=\pi \)
באופן דומה, נקבל \( \pi \) גם עבור קוסינוס. אבל רגע, זה לא מה שאנחנו רוצים, אם אנחנו רוצים בסיס אורתונורמלי! אנחנו רוצים לקבל 1! לכן מה שנעשה הוא לתקן קצת את המכפלה הפנימית - ההגדרה ה”נכונה” היא זו:
\( \left\langle f,g\right\rangle =\frac{1}{\pi}\int_{-\pi}^{\pi}f\left(x\right)g\left(x\right)dx \)
עכשיו כל הפונקציות הטריגונומטריות הן אורתונורמליות - כמעט. נשאר לנו עדיין המקרה של \( \cos\left(0x\right)=1 \). דווקא הפונקציה התמימה הזו אינה אורתונורמלית, כי \( \frac{1}{\pi}\int_{-\pi}^{\pi}dx=2 \). כדי לקבל פונקציה קבועה אורתונורמלית אצטרך לקחת את \( \frac{\sqrt{2}}{2} \) שלא נראית טוב במיוחד, אז מה עושים? נדבוק ב-\( \cos\left(0x\right) \) ופשוט יהיה לו מקדם קצת מוזר, כפי שתכף נראה.
עכשיו אנחנו מרוצים - הקבוצה \( \left\{ \sin nx\ |\ n\in\mathbb{N}\right\} \cup\left\{ \cos nx\ |\ n\in\mathbb{N}\right\} \) היא סדרה אורתונורמלית במרחב שלנו (שוב, למעט הקטע הזה עם הקבוע, שאינו בעייתי). אבל למעשה, היא יותר מזה - היא מה שקראתי לו סדרה אורתונורמלית שלמה, מה שאומר שאין איבר במרחב שאורתוגונלי לכל אבריה ושונה מאפס. ההוכחה של הטענה הזו מורכבת יותר ממה שעשיתי עד כה ואמנע ממנה לעת עתה כי זה פוסט מבוא שמנסה בעיקר להציג את הרעיונות ולא להוכיח דברים לעומק. מה שחשוב הוא המסקנה: כל פונקציה במרחב שלנו ניתנת לתיאור בתור צירוף לינארי אינסופי של אברי הקבוצה. את הצירוף הלינארי הזה נהוג לסמן בצורה הבאה:
\( f\left(x\right)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\cos nx+\sum_{n=1}^{\infty}b_{n}\sin nx \)
אבל צריך להיות זהירים מאוד לגבי האופן שבו אנחנו קוראים את הביטוי הזה. הוא נראה כאילו הוא אומר שלכל \( x \) שנציב באגף שמאל, נקבל את אותו מספר באגף ימין. זה לא נכון. השוויון פה אומר, פורמלית, שאם ניקח את אגף שמאל ונחסר ממנו את אגף ימין וניקח את הנורמה של כל זה במרחב שלנו, אז נקבל 0. זה מה שנקרא התכנסות בנורמה. השאלה מה קורה לכל \( x \) - שאלת ההתכנסות הנקודתית - היא מורכבת יותר ואתייחס אליה בהמשך.
קרוב לודאי שאתם תוהים למה כתבתי את המקדם החופשי בתור \( \frac{a_{0}}{2} \) ולא סתם בתור \( a_{0} \) - זה נובע מהבעיה של המקדם החופשי שדיברתי עליה ותכף נראה למה זה פותר אותה. בואו נדבר עכשיו על השאלה הבוערת - איך מוצאים את המקדמים הללו עבור פונקציה \( f \) קונקרטית? ובכן, מכיוון שהסדרה של הפונקציות הטריגונומטריות אורתונורמלית, אנחנו גם יודעים מה יהיו המקדמים: כזכור, אם \( e_{n} \) הוא איבר של סדרה אורתונורמלית, אז המקדם שלו בצירוף הלינארי שנותן את \( f \) הוא \( \left\langle f,e_{n}\right\rangle \). למקדם הזה קוראים - כמה הולם - מקדם פורייה של \( f \) (ביחס לסדרה הספציפית שלנו). כלומר, אנחנו מקבלים את הנוסחאות הבאות:
\( a_{n}=\left\langle f,\cos nx\right\rangle =\frac{1}{\pi}\int_{-\pi}^{\pi}f\left(x\right)\cos nxdx \)
\( b_{n}=\left\langle f,\sin nx\right\rangle =\frac{1}{\pi}\int_{-\pi}^{\pi}f\left(x\right)\sin nxdx \)
הנוסחאות הללו עובדות עבור \( n\ge1 \), אבל במקרה של \( a_{n} \) הינדסנו את הכל כדי שהיא תעבוד גם עבור \( a_{0} \). מה שקורה הוא שמכיוון ש-\( 1 \) אינה אורתונורמלית, אז \( \left\langle f,1\right\rangle \) לא יחזיר את המקדם של \( 1 \) בייצוג של \( f \), אלא את המקדם הזה כשהוא מוכפל בנורמה של 1, כלומר 2. כלומר המקדם צריך להיות \( \frac{a_{0}}{2} \) שבו אנו משתמשים, והכתיב המוזר הזה משתלם לנו כי יש לנו נוסחה יחידה עבור \( a_{n} \) בלי חלוקה למקרים.
עכשיו אפשר לשים את התיאוריה הכללית בצד לרגע ולראות מקרה פרטי, בעיניים. בלי לראות דוגמה קונקרטית ולהרגיש אותה כל העסק לא ממש שווה כלום, כי קשה לראות את ה”קסם”. מה שנעשה הוא לקחת פונקציה פשוטה, אבל כזו שבכלל לא מזכירה סינוסים וקוסינוסים פרט לכך שהיא מחזורית, ולראות איך יוצא טור הפורייה שלה. יותר חשוב מכך - לראות איך הטור הזה נראה כשמציירים אותו.
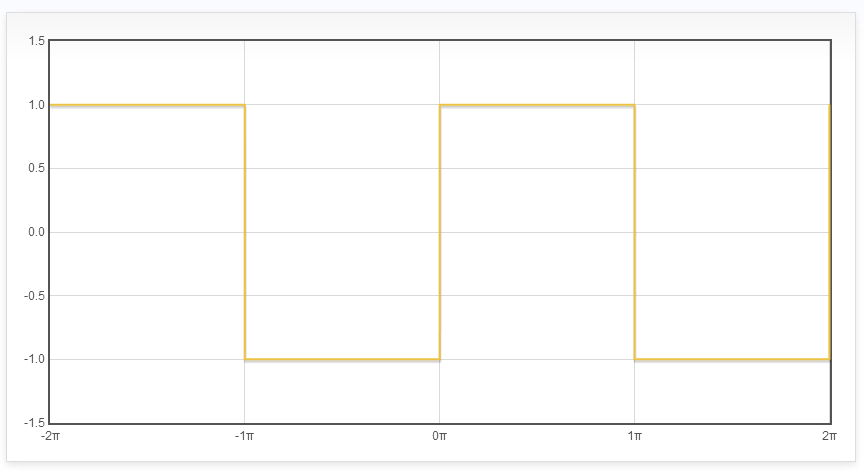
הפונקציה בסך הכל תקבל את הערכים 1 ו-\( -1 \), כשהיא מחליפה ביניהם אחרי מרחק של \( \pi \). כלומר, נגדיר
\( f\left(x\right)=\begin{cases}-1 & -\pi\le x<0\\1 & 0\le x\le\pi\end{cases} \)
וכמובן, אפשר להרחיב את הפונקציה הזו לכל \( \mathbb{R} \) באופן מחזורי (כלומר, שיתקיים \( f\left(x+2\pi\right)=f\left(x\right) \)). התוצאה היא פונקציה שנראית כך:
זה מזכיר את סינוס בכך שזו פונקציה מחזורית שהערכים המינימלי והמקסימלי שלה הם \( -1 \) ו-\( 1 \), אבל כאן הדמיון נגמר - סינוס עוברת בצורה רציפה בין כל הערכים שלה והפונקציה הזו לא; סינוס היא פונקציה עגולה ונחמדה, והפונקציה הזו ישרה. איך סכום של הרבה סינוסים יכול לתת לנו את הזוועה הזו?
ובכן, יש לנו נוסחה פשוטה לחישוב מקדמים, בואו נשתמש בה!
\( \left\langle f,\cos nx\right\rangle =\frac{1}{\pi}\int_{-\pi}^{\pi}f\left(x\right)\cos nx=\frac{1}{\pi}\left[\int_{-\pi}^{0}-\cos nxdx+\int_{0}^{\pi}\cos nxdx\right] \)
\( =\frac{2}{\pi}\int_{0}^{\pi}\mbox{cos}nxdx=0 \)
קיבלנו 0 כי, כזכור, \( \mbox{cos}nx \) הוא אנטיסימטרי סביב \( \frac{\pi}{2} \) וכל זה. ומה יקרה עם סינוס?
\( \left\langle f,\sin nx\right\rangle =\frac{2}{\pi}\int_{0}^{\pi}\mbox{sin}nxdx=\frac{2}{\pi}\left[-\frac{\cos nx}{n}\right]_{0}^{\pi}=\frac{2}{\pi}\left[\frac{-\cos n\pi+1}{n}\right] \)
עכשיו הכל תלוי בשאלה מהו \( \cos n\pi \). אם \( n \) זוגי, אז \( \cos n\pi=1 \); לעומת זאת, אם \( n \) אי זוגי אז \( \cos n\pi=-1 \). במקרה שבו \( n \) זוגי המונה יתאפס ונקבל מקדם 0; במקרה השני נקבל \( \frac{4}{\pi n} \). אם לסכם:
\( \left\langle f,\sin nx\right\rangle =\begin{cases}\frac{4}{\pi n} & n\equiv_{2}1\\0 & n\equiv_{2}0\end{cases} \)
ולכן אפשר לכתוב את טור הפורייה הבא:
\( f\left(x\right)=\frac{4}{\pi}\left(\sin x+\frac{1}{3}\sin3x+\frac{1}{5}\sin5x+\dots\right)=\frac{4}{\pi}\sum_{k=0}^{\infty}\frac{\sin\left(2k+1\right)x}{2k+1} \)
ושוב, זו אינה התכנסות נקודתית! כלומר, השוויון שכתוב שם לא אומר שהשוויון מתקיים לכל \( x \). קל לראות את זה, למשל, על ידי הצבת \( x=0 \): באגף שמאל נקבל \( 1 \) על פי הגדרת \( f \), אבל באגף ימין נקבל 0. אז את השוויון צריך להבין בתור התכנסות בנורמה - כפי שכבר אמרתי, ההפרש בין שני האגפים שואף לאפס כאשר מספר המחוברים באגף ימין שואף לאינסוף, כשהשאיפה לאפס היא על פי הנורמה שנובעת מהמכפלה הפנימית שהצגנו קודם.
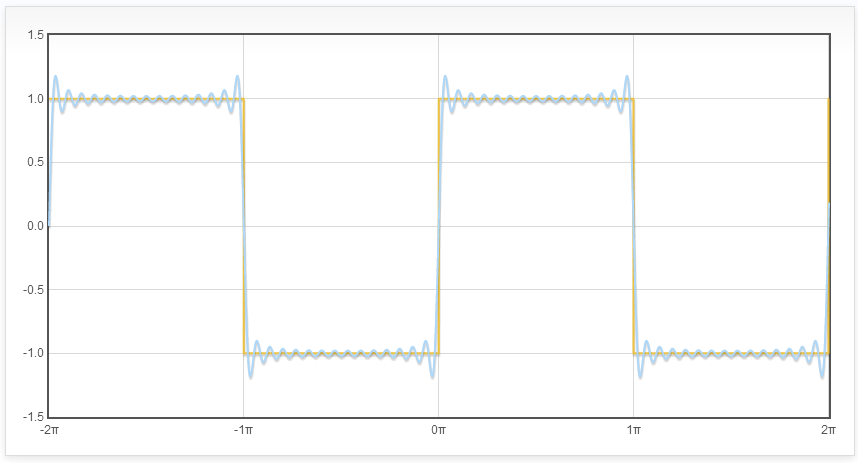
בואו ונראה איך נראה, למשל, סכום 15 האיברים הראשונים של הטור שבאגף ימין (בכחול):
זה נראה די טוב! המבנה הכללי זהה לזה של הפונקציה שאנחנו מנסים לקרב עם הטור. ה-0 ב-\( x=0 \) די ברור כעת - זה בדיוק השלב שבו הטור (שמגדיר פונקציה רציפה) “מטייל” בין \( 1 \) ל-\( -1 \). הדבר היחיד שנראה קצת מציק הוא הצ’ופצ’יקים הבולטים בקצוות של הקטעים, בדיוק ליד נקודות אי-הרציפות של הפונקציה המקורית. הצ’ופצ’יקים הללו נמצאים שם לא במקרה - מדובר על תופעה שנקראת אפקט גיבס ואולי אתאר מתישהו בפוסט נפרד. לבינתיים, הנה משהו שחלקכם יוכלו לשחק איתו: גרסה אינטראקטיבית של הטור שבה אתם יכולים לבחור את כמות האיברים בסכום ולראות מה קורה - איך מתרחש הקסם שבו אוסף של סינוסים הופך לאט לאט למשהו שנראה בדיוק כמו \( f \) (ושימו לב איך הקפיצה ליד נקודות אי הרציפות אמנם מתכווצת מבחינת הרוחב שלה, אבל הגובה שלה נותר תמיד מעל רמה מסויימת ולא טריוויאלית של שגיאה).
יש עוד נקודה שכדאי לתת עליה את הדעת בדוגמה שלי. אמרנו שטור פורייה הוא טור של סינוסים וקוסינוסים, אז איפה הקוסינוסים? ובכן, בחישוב הפורמלי ראינו שהמקדמים של כולם יצאו 0, אבל האם זה מקרי? כמובן שלא. \( f \) שלנו היא בבירור פונקציה אנטי-סימטרית סביב \( x=0 \) כמעט בכל נקודה, בדיוק כמו סינוס עצמה. זה מבטיח שהמקדמים של \( \cos x \) עבורה יצאו 0 ונקבל טור טיילור שהוא טור סינוסים בלבד. באופן דומה, פונקציה סימטרית תהיה בעלת טור קוסינוסים בלבד. בשני המקרים הסימטריה או האנטי-סימטריה לא חייבות להיות מושלמות - גם אם הן נכשלות במספר סופי של נקודות זה לא ישפיע על כלום כי אינטגרל של פונקציה לא משתנה אם משנים את הפונקציה במספר סופי של נקודות. יותר מכך, אם \( f \) היא אנטיסימטרית אז \( f\left(x\right)\sin nx \) היא סימטרית, ואם \( f \) סימטרית כך גם \( f\left(x\right)\cos nx \). זה אומר שאפשר לפשט טיפה את נוסחת האינטגרל ולהתעסק רק עם חצי מהתחום:
אם \( f \) אנטיסימטרית אז \( f\left(x\right)=\sum b_{n}\sin nx \) כאשר \( b_{n}=\frac{2}{\pi}\int_{0}^{\pi}f\left(x\right)\sin nxdx \)
אם \( f \) סימטרית אז \( f\left(x\right)=\sum a_{n}\cos nx \) כאשר \( a_{n}=\frac{2}{\pi}\int_{0}^{\pi}f\left(x\right)\cos nxdx \)
באופן כללי, כל פונקציה ניתן לתאר בתור סכום של פונקציה זוגית ופונקציה אי זוגית: אם \( f \) היא פונקציה כלשהי, אז \( \frac{f\left(x\right)+f\left(-x\right)}{2} \) היא פונקציה זוגית, \( \frac{f\left(x\right)-f\left(-x\right)}{2} \) היא פונקציה אי זוגית, ומתקיים \( f\left(x\right)=\frac{f\left(x\right)+f\left(-x\right)}{2}+\frac{f\left(x\right)-f\left(-x\right)}{2} \) (תרגיל נחמד: להוכיח שזה הייצוג היחיד של \( f \) כסכום של פונקציה זוגית ופונקציה אי זוגית). אז אפשר לחשוב על הסינוסים בטור הפורייה בתור הייצוג של החלק האנטי סימטרית ועל הקוסינוסים בתור הייצוג של החלק הסימטרי.
עכשיו בואו נעבור לדבר קצת על שאלת ההתכנסות הנקודתית. נניח ש-\( f\left(x\right)=\frac{a_{0}}{2}+\sum a_{n}\cos nx+\sum b_{n}\sin nx \), כשהשוויון מייצג, כרגיל, התכנסות בנורמה. מה בעצם הבעיה המרכזית שמונעת מאיתנו להיות בטוחים שיש גם התכנסות נקודתית? פשוט מאוד, העובדה שציינתי כבר קודם: המקדמים נקבעים על ידי חישוב של אינטגרל שכולל את \( f \); אבל אם נשנה את הערך של \( f \) בנקודה אחת, זה לא ישנה את הערך של האינטגרלים. בעצם, לכל טור פורייה \( \frac{a_{0}}{2}+\sum a_{n}\cos nx+\sum b_{n}\sin nx \) אנחנו מסוגלים למצוא מחלקה לא קטנה של פונקציות שמתוארות על ידו. אם תחשבו על זה רגע, תשימו לב שכל הפונקציות הללו יהיו במרחק 0 אחת מהשניה כשאנחנו מודדים מרחקים עם הנורמה שנובעת מהמכפלה הפנימית שלנו, וזה לא הכי תקין מתמטית כי פונקציית מרחק (“מטריקה”) אמורה להבטיח ששני איברים הם במרחק 0 אחד מהשני רק אם הם זהים. למטריקה שכושלת בעניין הזה קוראים “פסאודומטריקה” והדרך המקובלת “לתקן” אותה היא להגדיר יחס שקילות על אברי המרחב שלנו - שני איברים הם שקולים אם המרחק ביניהם הוא 0. עכשיו אפשר לעבור מהמרחב שלנו למרחב חדש, שהוא מרחב המנה שמתקבל מיחס השקילות הזה, ובו המטריקה תהיה תקינה. ועכשיו, איזה נציג אנחנו רוצים לבחור לכל מחלקת שקילות?
אתם לא חייבים להבין את כל הנאום שלמעלה כדי להבין את הרעיון: אותו טור פורייה מייצג כמה פונקציות שונות, והשאלה היא מי מביניהן היא הפונקציה ה”מוצלחת” ביותר, מבחינת זה שההתכנסות הנקודתית בה אופטימלית. באופן כללי זו גם לא שאלה טריוויאלית, אבל תחת תנאים מסויימים אפשר להבטיח התכנסות נקודתית. אתן אחד מהם שיחסית קל לנסח, למרות שיש עוד: אם הפונקציה רציפה וגזירה אז הטור שלה מתכנס אליה נקודתית. גם אם נקלקל ונוסיף נקודות אי רציפות של “קפיצה” בין שני ערכים, הטור עדיין יתכנס נקודתית פרט לנקודות אי הרציפות שבה הטור יתכנס לממוצע של שני הערכים (בדיוק מה שקרה עם הדוגמה שלנו). מה שכן, ההתכנסות הזו היא לא בהכרח התכנסות במידה שווה, למי שמכירים את המושג. לא פורמלית, התכנסות במידה שווה פירושו שאם נסכום מספיק איברים של הטור, אז לא תהיה לנו בשום מקום שגיאה “גדולה”. אפקט גיבס - הצ’ופצ’יקים ליד נקודות אי הרציפות - הוא דוגמה נגדית במקרה שלנו להתכנסות במידה שווה; ככל שנסכום יותר איברים כך הצ’ופצ’יק יתכווץ - יהיו פחות ערכים שבהם יש צ’ופצ’יק - אבל הוא לעולם לא יקטן מספיק בגובה שלו, כלומר תמיד תהיה נקודה כלשהי שבה יש שגיאה גדולה יחסית (אם נחבר עוד ערכים אז הנקודה הזו תהפוך למדוייקת יותר, אבל עדיין תהיה נקודה אחרת שבה יש שגיאה גדולה).
מה על פונקציות שהן “סתם” רציפות, בלי הנחות מיוחדות לגבי הנגזרת שלהן? רציפות היא תכונה מאוד נחמדה מצד אחד, שמונעת מאיתנו “לקלקל” פונקציות בצורה נקודתית כדי להבטיח שטור הפורייה שלהן יטעה באותן נקודות - אבל עדיין, אם אין לנו שליטה על גודל הנגזרת, הפונקציה יכולה להיות די משוגעת. לא אתן דוגמאות נגדיות מפורשות, אבל ניתן לבנות פונקציות רציפות שטור הפורייה שלהן בכלל לא מתכנס נקודתית בשום מקום. אז מה עושים? ובכן, מסתבר שגרסה יותר כללית של התכנסות עדיין עובדת כאן. בואו נסתכל שניה על סדרת הסכומים החלקיים של טור פורייה כלשהו, כלומר נגדיר \( S_{m}\left(x\right)=\frac{a_{0}}{2}+\sum_{n=1}^{m}\left(a_{n}\cos nx+b_{n}\sin nx\right) \). ייתכן, כאמור, שהסדרה \( S_{0}\left(x\right),S_{1}\left(x\right),S_{2}\left(x\right),\dots \) לא מתכנסת בכלל עבור ערכים מסויימים של \( x \), אבל אפשר להסתכל על סדרת הממוצעים שלה:
\( \sigma_{m}\left(x\right)=\frac{S_{0}\left(x\right)+\dots+S_{m}\left(x\right)}{m+1} \)
ניתן להוכיח - ושוב, לא אעשה זאת כרגע - שאם \( f \) היא פונקציה רציפה ואנו סוכמים את טור הפורייה שלה בצורה הזו של סדרת הממוצעים, אז הסכום הזה מתכנס לערך של \( f \) בכל נקודה שבה \( f \) רציפה. שיטת הסכימה הזו - סכימה של הממוצעים - נקראת “סכימת צזארו” והזכרתי אותה לא מזמן בפוסט שעסק בשוויון המוזר \( 1+2+3+\dots=-\frac{1}{12} \). שם הסכימה הזו נתנה את הסכום הלא אינטואיטיבי \( 1-1+1-1+1-\dots=\frac{1}{2} \), ולא מעט אנשים התקשו לקבל אותו כלגיטימי; אני מקווה שהשימוש הנוכחי של סכימת צזארו, שמראה שאפשר עם קצת תושייה לשחזר את הפונקציה המקורית גם מתוך טור פורייה שאינו מתכנס נקודתית, יסייע קצת להפחתת הסקפטיות בנוגע לשיטת הסכימה הנחמדה הזו.
לסיום הפוסט הזה אני רוצה לחשב את טור הפורייה של עוד פונקציה פשוטה - מכיוון שהחישוב הזה יניב תוצאה יפה ולא טריוויאלית (שכבר הראיתי בבלוג בדיוק באותו האופן אבל מי זוכר). הפונקציה היא \( f\left(x\right)=x \) בתחום \( \left[-\pi,\pi\right] \). זו פונקציה אנטיסימטרית ולכן הפיתוח שלה הוא לטור סינוסים \( f\left(x\right)=\sum b_{n}\sin nx \) כאשר \( b_{n} \) נתון על ידי האינטגרל \( \frac{2}{\pi}\int_{0}^{\pi}x\sin nxdx \). זה לא אינטגרל מסובך, אבל צריך להשתמש בתעלול אינטגרציה בסיסי בשבילו - אינטגרציה בחלקים. נקבל:
\( \int_{0}^{\pi}x\sin nxdx=\left[-\frac{x\cos nx}{n}\right]_{0}^{\pi}-\int_{0}^{\pi}\frac{\cos nx}{n}dx=\left(-1\right)^{n+1}\frac{\pi}{n} \)
(האינטגרל עם הקוסינוס מתאפס, כפי שכבר ראינו לא מעט בפוסט)
מסקנה, אחרי שנכפול מחדש ב-\( \frac{2}{\pi} \): \( b_{n}=\frac{2}{n}\left(-1\right)^{n+1} \). כלומר, ניתן לכתוב את הטור במפורש כך:
\( x=2\sin x-\sin2x+\frac{2}{3}\sin3x-\frac{1}{2}\sin4x+\dots \)
אבל זה לא מה שנחמד. מה שנחמד הוא מה שקורה כאשר אנחנו מחשבים את הנורמה של הפונקציה הזו. בואו נחשב אותה לרגע בצורה ישירה:
\( \|x\|^{2}=\frac{1}{\pi}\int_{-\pi}^{\pi}x^{2}dx=\frac{1}{\pi}\left[\frac{x^{3}}{3}\right]_{-\pi}^{\pi}=\frac{1}{\pi}\frac{\pi^{3}+\pi^{3}}{3}=\frac{2}{3}\pi^{2} \)
עדיין לא נראה מעניין במיוחד, אבל אפשר להשתמש ב”משפט פיתגורס” של מרחבי מכפלה פנימית אינסוף ממדיים - שוויון פרסבל, שאומר שאם \( f=\sum a_{n}e_{n} \) כאשר \( e_{n} \) הם אברי בסיס אורתונורמלי, אז \( \|f\|^{2}=\sum a_{n}^{2} \). במקרה שלנו, \( b_{n}^{2}=\frac{4}{n^{2}} \), אז קיבלנו את השוויון הבא:
\( \frac{2}{3}\pi^{2}=\sum_{n=1}^{\infty}\frac{4}{n^{2}} \)
ועל ידי חלוקה ב-4 של שני האגפים נקבל:
\( \sum_{n=1}^{\infty}\frac{1}{n^{2}}=\frac{\pi^{2}}{6} \)
השוויון הזה הוא אחת התוצאות החביבות עלי במתמטיקה - באגף שמאל יש לנו את אחד הטורים המתכנסים הפשוטים ביותר. על פניו בכלל לא ברור איך לחשב את סכומו; ופתאום, באגף ימין יש לנו את הסכום באופן מדויק, וצץ שם \( \pi \) השד יודע מאיפה למרות שלסכום הזה אין לכאורה שום קשר למעגלים. לדעתי זה נפלא. אם אתם רוצים לראות עוד הוכחות (ההוכחה של אוילר נפלאה אפילו עוד יותר) - כאמור, כבר יש לי פוסט על התוצאה הזו. עם זאת, אפשר להשתמש בטורי פורייה של פונקציות נוספות כדי לקבל עוד סכומים דומים, אבל לבינתיים נראה לי שהנקודה הובהרה.
נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: