על משוואות בלי פתרון, ולמה זה לא רציונלי

בניית מערכת המספרים שלנו הגיעה בפעם הקודמת לנקודת שיא מסויימת - קיבלנו את השדה (ממציין 0…) הקטן ביותר - ולכן גם האובייקט הבסיסי בענף של תורת השדות. משמעות המילה “שדה” היא שקיבלנו סגירות לארבע פעולות החשבון הבסיסיות, ולכן גם את היכולת לפתור כל משוואה ממעלה ראשונה. אולם הצרות מתחילות כבר במשוואות ממעלה שנייה - ולמעשה, עד שנגיע אל המרוכבים הן לא ייפתרו לגמרי. הבעיה הראשונה היא כבר במשוואה \( x^2-2=0 \) שאין לה פתרון: את המספר שאנו מכנים “שורש שתיים”, שמשמעותו היא “המספר החיובי שכשמעלים אותו בריבוע מקבלים שתיים” לא ניתן להציג בתור מספר רציונלי - כלומר, בתור מנה של שני מספרים שלמים. מכאן שהוא לא מספר רציונלי, או כפי שנהוג לומר - הוא מספר אי רציונלי (Irrational).

כאן נשאלת השאלה הפשוטה - רגע, אם אנחנו קוראים “מספרים” רק לדברים שבנינו עד עכשיו, ומה שאנחנו קוראים לו “שורש שתיים” לא מתאים בכלל להגדרה הזו, למה אנחנו קוראים לו “מספר”? לא עדיף לומר שאין כזה דבר, שורש שתיים?

ייתכן שהשאלה הזו נראית מעט מוזרה לנו, שהתרגלנו לחשוב על שורש שתיים כדבר מה קיים: פשוט לוקחים את הספרה 2, מציירים מעליה \( \sqrt{2} \), וחסל! אלא שכמובן שהדברים אינם עובדים בדרך הזו; אם הנימוק הזה היה מקובל עלינו, היה עלינו לקבל מייד גם את קיומם של המספרים המרוכבים: פשוט לוקחים את המספר “מינוס אחד” (שאין לנו ספק יותר - אני מקווה - שקיים), מציירים מעליו שורש, וחסל. אם כן, בינתיים שורש שתיים מוטל בספק לפחות כמו i הידוע לשמצה.

אולם יש לשורש שתיים יתרון עצום, שאין ל-i המסכן: יש לו אינטואיציה גאומטרית, ואחת חזקה מאוד.

כשאנו מציירים קטע, אנו מייחסים לו אוטומטית מספר כלשהו - ה”אורך” שלו. המשמעות הפורמלית של המושג הזה לא ברורה בכלל, אבל המשמעות האינטואיטיבית (שהיא זו שמעניינת אותנו כאן) ברורה לחלוטין - ומבלי שנרד לעומקם של דברים, אנו (טוב, לפחות אני) מרגישים שהאורך הזה “קיים” במובן שבו מספרים קיימים. (אגב, שימו לב לכך שהדבר נותן משמעות רק למספרים חיוביים - איננו מכירים קטעים בעלי אורך שלילי, ואפילו לא בעלי אורך אפס, למרות ש”נקודה” היא מועמד טוב לכך - אבל זה כבר דיון פילוסופי אחר לגמרי). 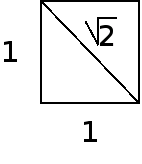כעת, אחת מהצורות הגיאומטריות הפשוטות ביותר היא הריבוע - יצור המורכב מארבעה קטעים באותו אורך המתחברים זה לזה בזוויות ישרות. נסמן את אורך כל אחד מהקטעים הללו בתור “1”. זוהי בחירה שרירותית, שפירושה שנמדוד אורכי קטעים אחרים ביחס לצלע הריבוע: כך למשל אם קטע כלשהו הוא מאורך “2” פירוש הדבר הוא שאורכו כפול מאורך צלע הריבוע. גם למספרים רציונליים קל לחשוב על משמעות: אם קטע כלשהו הוא באורך 3/5, פירוש הדבר הוא שאורכו כפול חמש שווה בגודלו לאורך צלע הריבוע כפול שלוש. בגישה אחרת, ניתן לומר שזה אומר שקיים קטע קטן עוד יותר, שנכנס מספר שלם של פעמים הן בצלע הריבוע והן בקטע שאורכו 3/5 - במקרה שלנו קטע זה הוא 1/5, שנכנס שלוש פעמים בקטע שבאורך 3/5, וחמש פעמים בצלע הריבוע. אם קטע קטן משותף שכזה קיים עבור שני קטעים, אומרים שיש להם מידה משותפת. לא קשה להראות (נסו!) שאם יש לקטע כלשהו מידה משותפת עם קטע באורך 1, אורכו של קטע זה הוא מספר רציונלי. והנה, כבר בריבוע החביב צץ לנו מושג האי רציונליות ישר לפרצוף, ועוד עם הקטע הבסיסי ביותר שניתן לחשוב עליו בריבוע פרט לצלעות - האלכסון. הקו שמחבר שני קודקודים מנוגדים. גיאומטריה אלמנטרית אומרת לנו שהאלכסון הוא היתר במשולש ישר זווית (ששוקיו הן שתיים מצלעות הריבוע), ואנו משתמשים במשפט פיתגורס (שלא אוכיח כאן, אך אני מקווה שאתם מקבלים כנכון - יש לו למעלה ממאה הוכחות שונות!) כדי לקבל שאורך האלכסון הוא \( \sqrt{1^2+1^2}=\sqrt{2} \).

וכאן, כאמור, מגיע הבוקס לפנים, שכן שורש שתיים אינו רציונלי - ובמילים אחרות, אין לאלכסון הריבוע מידה משותפת עם צלע הריבוע.

התגלית הזו מיוחסת כבר לפיתגוראים - תלמידיו (ויש שיאמרו חסידיו הקנאים) של פיתגורס, שחיו בסביבות השנים 500 לפנה”ס. חשוב לציין שהתגלית בניסוחה המקורי דיברה על “אין מידה משותפת” ולא על “המספר שורש שתיים הוא אי רציונלי” - מושג המספר לא היה קיים אצל הפיתגוראים בצורה שבה אנו מכירים בו כיום, והם חשבו על “מספר” בתור אורך של קטע. מפאת חוסר בקיאות לא אכנס כאן לתורה המיסטית השלמה שפיתחו הפיתגוראים סביב המספרים שלהם - רק אומר שהיא התבססה במידה רבה על מספרים שניתן להביע בתור יחסים בין מספרים שלמים, ולכן גילוי המספרים האי רציונליים היווה מכה עבורם, והאגדות מספרות שהם הטביעו את זה מביניהם שגילה את ה”סוד” לעולם הרחב (אגב, איני בטוח אם התגלית אכן הייתה על אלכסון הריבוע - בגרסה אחרת ששמעתי, התגלית הגיעה בכלל מאורך של קטע בתוך פנטגרם - מה ששקול להוכחה ששורש חמש אינו רציונלי, לא שורש שתיים).

העובדה שאלכסון הריבוע הוא יצור גאומטרי שאיננו מטילים ספק רב בקיומו מונעת מאיתנו לומר “זה לא הגיוני, ולכן אין אורך לאלכסון הריבוע”, ואכן - כדאי להבהיר ש”מספר אי רציונלי” אין פירושו “מספר לא הגיוני”, ממש כפי שפירוש “מספר רציונלי” אין פירושו “מספר הגיוני”. עם זאת, האטימולוגיה של המילה ratio היא (בערך) במילה הלטינית של “לחשב”, ויש הגיון מאחורי הדבר - אין ייצוג סופי “פשוט” למספר אי רציונלי - כאמור, לא ניתן לייצג אותו כמנה בין שני מספרים שלמים, ואם מנסים לכתוב אותו כשבר עשרוני (או בכל בסיס ספירה אחר), אין קץ למספר הספרות שצריך לכתוב, ואין בהן מחזוריות.

טוב ויפה, אבל למה בעצם שורש 2 הוא אי רציונלי? ההוכחה לכך (זו האלגברית המקובלת כיום, לא הגאומטרית) פשוטה עד להפתיע, והיא זכתה לכך שהמתמטיקאי האנגלי בן המאה העשרים, ג’.ה. הארדי (G. H. Hardy) יכלול אותה בתור דוגמה ל”יופי מתמטי” בספרו “התנצלותו של מתמטיקאי” (A Mathematician’s Apology) (המילה “התנצלות” אולי אינה מדוייקת, שכן הכוונה אינה ל”בקשת סליחה”, אלא להצדקה - אולם “הצטדקותו של מתמטיקאי” נשמע גרוע אף יותר). קטונתי מלהיות הארדי, אבל אנסה גם אני להעביר כאן את פרטי ההוכחה.

השיטה שבה נפעל היא “הוכחה בדרך השלילה” - נניח שהטענה שאנו מבקשים להוכיח אינה נכונה, ונגיע מההנחה הזו למשהו שאנו יודעים בודאות שהוא שגוי. מכיוון שהוא שגוי, אחת מהנחותינו בטעות יסודה - ומכיוון שאנו פחות או יותר בטוחים בקשר לכל ההנחות פרט לזו הנוגעת לטענה שאנו מנסים להוכיח, אנו מסיקים שההנחה שהיא אינה נכונה הייתה טעות. למרות שזו דרך הוכחה בסיסית ומקובלת במתמטיקה, יש גם כאלו שאינם מקבלים אותה, וגם אתם אינכם חייבים.

ובכן, נניח ששורש 2 הוא כן רציונלי, אז קיימים שני מספרים שלמים, a,b ששורש שתיים הוא מנתם: \( \sqrt{2}=\frac{a}{b} \). ייתכן שאתם זוכרים מפוסט קודם משהו שאמרתי על כך שלאותו מספר רציונלי יש מספר רב של ייצוגים, ושבוחרים לעתים קרובות ייצוג “קנוני” של שבר מצומצם, כלומר שבו a,b לא מתחלקים באף מספר משותף חוץ מ-1 - ובכן, זה אחד מהמקרים הללו. ה”משהו שאנו יודעים בודאות שהוא שגוי” שנגיע אליו הוא שדווקא כן קיים מחלק משותף ל-a ול-b - במקרה הזה, המספר 2.

ראשית, נעלה בריבוע את שני אגפי השוויון שראינו קודם, ונקבל \( 2=\frac{a^2}{b^2} \). נעביר אגפים ונקבל \( 2b^2=a^2 \). פירוש הדבר הוא שהמספר \( a^2 \) הוא זוגי - כי הצגנו אותו בתור מספר כלשהו כפול 2.

כעת, לא קשה להוכיח (נסו!) שאם מעלים מספר זוגי בריבוע מקבלים מספר זוגי, ואילו אם מעלים מספר אי זוגי בריבוע מקבלים מספר אי זוגי. לכן, אם \( a^2 \) זוגי, בהכרח גם \( a \) זוגי. כלומר, אפשר לכתוב \( a=2t \) כאשר t הוא מספר שלם כלשהו.

אבל מה קיבלנו כעת? קיבלנו ש-\( 2b^2=a^2=(2t)^2=4t^2 \) ולכן, לאחר צמצום ב-2, נקבל \( b^2=2t \). מכאן שגם b זוגי - ולכן גם הוא וגם a מתחלקים ב-2, וזו הסתירה המבוקשת. אם כן, ראינו בעיה אחת שיש לשדה המספרים הרציונליים. יש דרך לא רעה להתגבר על בעיה זו, ולהבטיח שלכל משוואה פולינומית יש פתרון. בפרט, דרך זו מכניסה לתמונה ישר גם את i הידוע לשמצה. אלא שלא זו הדרך שבה נלך.

במקום זאת, נצביע על בעיות נוספות, לא אלגבריות, שיש למספרים הרציונליים, ועל הדרך המקובלת לפתור אותן - פתרון שיחסל את בעיית שורש שתיים לחלוטין, אבל ישאיר את בעיית השורש של מינוס אחת על כנה. לפתרון הזה קוראים “המספרים הממשיים”.