צ’ומפ צ’ומפ

בתגובה לאחד מהפוסטים הקודמים הזכיר לי אלון עמית את אחת הדוגמאות האלגנטיות והיפות ביותר שאני מכיר להוכחה לא קונסטרוקטיבית, ואני סבור שהיא מתאימה מאוד לסיום העיסוק בהוכחות לא קונסטרוקטיביות (לפחות לעת עתה). כוכב הדוגמה הוא משחק מטופש ותמים ביותר בשם Chomp.

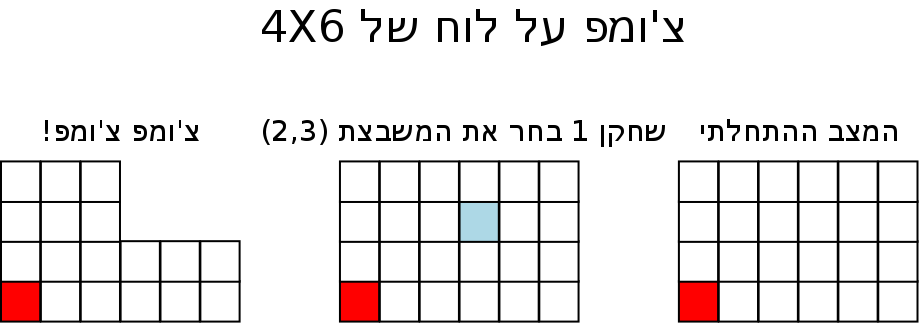
המשחק הולך כך: לוח המשחק הוא מלבן הבנוי מריבועים (ממדי המלבן יכולים להשתנות ממשחק למשחק - זה מה שלכאורה מוסיף אתגר). ישנם שני שחקנים המשחקים לסירוגין. בכל סיבוב אחד השחקנים בוחר אחת מהמשבצות, ומסיר מהלוח אותה ואת כל המשבצות שנמצאות במלבן שהיא הפינה השמאלית התחתונה שלו - במילים אחרות, כל משבצת שנמצאת לימינה או מעליה.

המשבצת השמאלית התחתונה ביותר בלוח היא “מורעלת” - מי שלוקח אותה, הפסיד. לכן, מטרת המשחק היא לגרום ליריב לקחת אותה. בכך המשחק מזכיר מעט את המשחק “נים”, שגם בו המטרה היא לא להיות זה שלוקח את האובייקט האחרון.

מה שהופך את המשחק הזה למעניין היא העובדה שאפשר להוכיח (בצורה פשוטה ביותר) שהשחקן שפותח תמיד יכול לנצח במשחק (בכל לוח, ובלי תלות בשאלה מה עושה השחקן השני), אבל ההוכחה הזו אינה קונסטרוקטיבית; היא אינה מצביעה כלל על הדרך שבה השחקן הזה צריך לשחק כדי לנצח.

ההוכחה עצמה היא טריוויאלית, אבל היא מתבססת על משפט ידוע ומוכר מתורת המשחקים - משפט צרמלו. המשפט מוצג במספר וריאציות (שכולן די שונות מהנוסח המקורי של צרמלו עצמו), ואציג כאן אחת מהפשוטות שבהן, אשר ממנה נובע שב-Chomp אחד משני השחקנים בהכרח מסוגל לנצח בלי תלות במה שעושה היריב.

לפני כן כדאי לומר מילה או שתיים על המושג המתמטי של “משחק”. בהגדרה מקושקשת משהו אפשר לומר ש”משחק” הוא כל סיטואציה בה משתתף אחד או יותר נוקט בסדרה של החלטות כדי להגיע לתוצאה שהיא אופטימלית בעיניו. מילת המפתח כאן היא “החלטה” - אם אין החלטות, המשחק די חסר טעם.

משחקים לשחקן יחיד לא חסרים, ושלוש הדוגמאות המוכרות של ימינו, באדיבותה של חברת מיקרוסופט, הן סוליטייר, פריסל ושולה המוקשים. עם זאת, העניין האמיתי מתעורר כאשר יש שני שחקנים או יותר - במצב זה, השחקן אינו תלוי רק בעצמו כדי לקבוע את תוצאת המשחק; הוא צריך להביא בחשבון גם את מה שהשחקנים האחרים יעשו.

כאשר רוצים לתאר משחק בצורה מתמטית, ישנן מספר דרכים לעשות זאת. גישה אחת, שנכנסת אל תוך המכניקות הפנימיות של המשחק, מתארת אותו בתור עץ מכוון שכל צומת בו מייצג סיטואציה אפשרית כלשהי במשחק (למשל, השורש שלו מייצג את המצב ההתחלתי של המשחק, והעלים את סוף המשחק) ויש קשת מצומת אחד לצומת שני אם בחירות השחקנים במצב שמגולם באב יכולות להוביל למצב שמגולם בבן (יש לשים לב כי גם לאותו מצב בלוח עשויים להיות כמה וכמה צמתים שונים בעץ, שכן צומת בעץ מייצג לא רק את המצב אלא גם את הדרך שבה הגענו אליו).

באמצעות דרך הייצוג הזו קל להוכיח את הגרסה שלנו של משפט צרמלו, שגורסת כי במשחק סופי (כזה שתמיד נגמר) לשני שחקנים שמשחקים לסירוגין, עם ידיעה גמורה, שבו התוצאות האפשריות היחידות הן ניצחון לאחד משני השחקנים (נקרא להם מעכשיו “הלבן” ו”השחור”, כמו בשחמט, כדי לפשט, כאשר “הלבן” הוא זה שמתחיל), בהכרח אחד מהשחקנים מסוגל לכפות ניצחון בלי תלות במעשי השני.

המונח הבעייתי היחיד בניסוח המשפט הוא “ידיעה גמורה”. משמעותו היא שבכל סיבוב השחקנים יודעים בדיוק היכן בעץ המשחק הם נמצאים, ואילו פעולות עליהם לנקוט כדי לעבור לצומת הבא. בפועל פירוש הדבר הוא שבמשחק אין מידע מוסתר (למשל, בטקטיקו מוסתרים מכל שחקן הכלים של השחקן השני, ובשולה המוקשים יש משבצות שלא ניתן לדעת את תוכנן וחייבים לנחש), ואין מימד של אקראיות (למשל, במונופול השחקנים מתקדמים על ידי הטלת קובייה). אפשר לסלק את האקראיות ולהישאר רק עם חוסר ודאות על ידי כך שחושבים על סדרת האקראיות כאילו כבר “נקבעה מראש” והיא פשוט לא ידועה, אך לא ניכנס לזה.

הדרך להוכיח שאחד משני השחקנים יכול לכפות ניצחון היא זו: ראשית, כל עלה בעץ מסמל ניצחון במשחק של אחד השחקנים (כי המשחק חייב להסתיים בניצחון). אם כן, נסמן ב-1 את העלים שמסמלים ניצחון של השחקן הלבן, וב-0 עלים שמסמלים ניצחון של השחור. כעת, באופן אינדוקטיבי, נסמן גם את שאר הצמתים בעץ במספרים: בהינתן צומת שמסמל סיטואציה במשחק בה תורו של השחקן הלבן, הסימון שבצומת יהיה פונקצית “או” של כל הבנים של הצומת (כלומר, 1 אם אחד מהם הוא 1, ו-0 אם כולם 0), ובהינתן צומת שמסמל את תורו של השחקן השחור, הפונקציה תהיה “וגם” (1 רק אם כולם 1, 0 אם אחד מהם 0).

בצורה הזו מסומן כל העץ, ובפרט השורש. אם השורש מסומן ב-1, הלבן יכול לכפות ניצחון. אם הוא מסומן ב-0, השחור יכול לכפות ניצחון.

למה? כי נניח שהשורש מסומן ב-1, וזה צומת שמסמל מהלך של הלבן (כי הלבן מתחיל). פירוש הדבר שלפחות אחד מבניו הוא 1. הוא יבחר במהלך במשחק שמביא אותו לבן הזה. עכשיו תור השחור. הוא בצומת שמסומן 1, ולכן כל בניו של הצומת הם 1, ולכן בלי קשר לשאלה מה יבחר לעשות השחקן השחור, הוא עדיין יגיע לצומת של 1. שוב תור השחקן הלבן, והוא שוב ימשיך לצומת שמסומן ב-1 וכן הלאה. האינוריאנטה נשמרת; המשחק תמיד נמצא בצומת שמסומן ב-1. מכיוון שהמשחק סופי, מתישהו יגיע הטיול בעץ לעלה, ובשל האינוריאנטה העלה יהיה מסומן ב-1 - כלומר, הלבן ניצח, בלי תלות במה שעשה השחור. החשיבות היחידה הייתה לבחירות שהלבן ביצע במהלך כל הטיול בעץ. לסדרה הכוללת של הבחירות שהיה עליו לבצע (“אם השחור ביצע את המהלך הזה, עשה כך וכך. אם השחור עשה דווקא את זה, אז עשה כך וכך וכך”) קוראים אסטרטגיה.

אם השורש הוא 0, ההוכחה דומה; נסו לחשוב על הפרטים בעצמכם.

וכעת חזרה לצ’ומפ, כשאנחנו משוכנעים שאו הלבן יכול לכפות ניצחון, או השחור. אני רוצה להוכיח שבהכרח הלבן יכול לכפות ניצחון. ההוכחה היא כדלהלן:

נניח בשלילה שדווקא השחור יכול לכפות ניצחון, כלומר יש לו אסטרטגיה שמבטיחה ניצחון לכל פעולה של הלבן. בפרט, יש לו תגובה שתבטיח ניצחון למשחק של הלבן שבו הצעד הראשון הוא בחירת המשבצת הימנית העליונה בלוח.

כעת, אנחנו לא יודעים מה הצעד של השחור יהיה, ומה הוא המשך האסטרטגיה שלו, אבל אנחנו יודעים בודאות שהלבן יכול “לגנוב” אותם. איך? נניח לרגע שהמהלך של השחור מתחיל בבחירת המשבצת בקוארדינטה (2,3), ומכאן והלאה תגובה הולמת לכל מהלך של הלבן. אז הלבן יכול להתחיל את המשחק בכך שיבחר את הקוארדינטה (2,3), ומכאן והלאה יפעל על פי האסטרטגיה המנצחת של השחור.

מקור הכוח של הלבן הוא שבחירת הקוארדינטה (1,1) לא באמת משפיע על כלום. זה “מהלך סרק” - לא משנה איזה מהלך השחור יבצע כעת, הלוח בסיום המהלך הזה יהיה זהה ללוח שהלבן יכל להגיע אליו על ידי ביצוע אותו מהלך של השחור כבר בסיבוב הראשון.

אם, למשל, הלבן היה בוחר את (2,2) בסיבוב הראשון, התעלול לא היה פועל: השחור היה מסוגל לבחור משבצת כלשהי כך שהלוח אחרי בחירתה היה במצב שאליו הלבן לא מסוגל להגיע בסיבוב הראשון - נסו לחשוב על מהלך שכזה.

אם כן, הפרכנו את הטענה שלשחור יש אסטרטגיה מנצחת, ולכן על פי משפט צרמלו זהו הלבן שיש לו אסטרטגיה מנצחת, וגמרנו. רק מה? לא אמרנו שום דבר על מהי האסטרטגיה הזו - אפילו את המהלך הראשון שלה איננו יודעים. המשחק מכור מראש למרות שאין לנו מושג איך.

רק הערה כללית לסיום: משפט צרמלו שהוצג כאן תקף גם למשחקים עם תוצאת תיקו (ההכללה מיידית - תנו ערך 1 לניצחון של הלבן, 0 לתיקו ומינוס 1 לניצחון של השחור, ובחרו בצמתים פונקציות של “מקסימום” ללבן ו”מינימום” לשחור), ולכן תקף לשחמט ולדמקה. בכל הנוגע לשחמט, איש אינו יודע איזו מבין שלוש האפשרויות נכונה (האם הלבן יכול לכפות ניצחון, השחור יכול לכפות ניצחון, או כל אחד יכול לכפות תיקו) ומכיוון שעץ המשחק של שחמט הוא עצום בגודלו, גם לא סביר שפתרון יתגלה כל כך מהר, אבל דמקה כבר “פוצחה” בצורה הזו לא מזמן (או לפחות כך נטען) והוכח שכל שחקן בה מסוגל לכפות תיקו.

אני מודה שאיני יודע אם התגלית הזו משמחת או מדכאת אותי.