השארת הרצף

ריצוף הוא מאותם נושאים מתמטים שקיים סיכוי שגם לא-מתמטיקאים יוכלו להבין ולהינות ממנו בקלות רבה יחסית; בסופו של דבר, אנו נתקלים בריצופים בכל עת בחיי היום-יום, וגם באמנות הם לא חסרים (ומובאים לשיא ביצירותיו של אשר, שאחת מהן מוצגת למעלה).

הרעיון הבסיסי פשוט - יש לנו את המישור הדו-ממדי (למשל, הרצפה בחדר שלנו), והוא יכול להיות סופי ותחום בצורה כלשהי, או אינסופי. כמו כן יש לנו קבוצה כלשהי של אריחים (Tiles), ואנחנו רוצים להניח אותם על השטח שאנו מנסים לרצף בצורה כזו שכל השטח יהיה מכוסה, לא יהיו שני אריחים שעולים אחד על השני, ואולי גם יתקיימו תנאים נוספים שנדרשים מהריצוף.

אני מסוגל לחשוב מיידית על מספר משחקי ריצוף שכאלו שאתם בוודאי מכירים. בראשון נתונות מספר צורות שונות ומשונות והמטרה היא לסדר אותן כך שיצרו ריבוע, מלבן, או משהו דומה. הנה דוגמה למשחק שכזה, שבו הצורות יוצרות “כמעט ריבוע” (ריבוע שהפינות הוסרו ממנו):

אבני המשחק כאן מורכבות מריבועים שחוברו זה לזה, ומכונות “פוליומינוס” (Polyominoes). אולי ארחיב על האבנים הללו (שהן גם כוכבות המשחק “טטריס” כשמרכיבים אותן בדיוק 4 ריבועים) בעתיד.

דוגמה אחרת, שונה למדי, היא זו של פאזל (Jigsaw). כל פאזל הוא משחק ריצוף “קיצוני” למדי בכך שלכל חתיכה יש מיקום מוגדר מאוד, ומספר קטן של חתיכות שאפשר להתחבר אליהן. זה גם הופך את הבעיה של פתרון פאזל לקלה בהרבה ממשחק הפוליומינוס שהוצג למעלה - יש פחות אפשרויות לבחור. לכן, במובן מסויים, פאזלים הם “משעממים” מבחינה חישובית. עוד דוגמה למשחק ריצוף הוא סודוקו - כמו בפאזל, כך גם כאן המגבלה העיקרית היא מגבלה מלאכותית שמושתת על המשחק, ולא הצורה של האבנים שמחברים.

עוד סוג של פאזל הוא מה שאכנה, בשל מחסור בשם טוב יותר (מישהו מכיר?) בשם “פאזל-9”. משחק פאזל שבו יש רק 9 ריבועים, אבל אין לקצות הריבועים צורה ייחודית; במקום זה, כל אחד מארבעת צדדיו של כל ריבוע מכיל חצי תמונה, והמטרה היא לחבר את הריבועים כך שכל התמונות משלימות זו את זו. מכיוון שאותם חצאי תמונה חוזרים מספר פעמים בצירופים שונים, המשחק מתגלה כמאתגר למדי.

המשחק הזה מוביל אותי לנושא העיקרי שעליו רציתי לדבר - Wang tiles, שאכנה מעכשיו פשוט בתור “אריחי וונג”.

אריח וונג הוא יצור דומה לריבועים שבפאזל - ריבוע שכל ארבעת צדדיו צבועים בצבע כלשהו (או מכילים תמונה, או מספר, או אות - מה שתרצו). הנה הדוגמה הבלתי נמנעת:

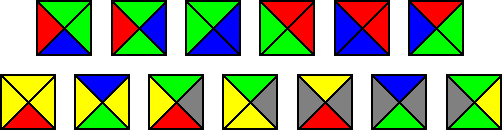
גם עם האריחים הללו אנו משחקים משחקי ריצוף, כשהכלל הוא פשוט - מותר להניח שני ריבועים זה ליד זה רק אם הצלעות שלהם שנוגעות זו בזו צבועות באותו הצבע (שימו לב שמדובר בהגבלה מעט שונה מאשר זו של הפאזל-9).

אריחי וונג (הנקראים כך על שם Hao Wang, שחקר אותם) היו ועודם נושא למחקר רציני במדעי המחשב. יש להם שימושים כלשהם בגרפיקה ממוחשבת (ריצוף וונג יכול לאפשר יצירה של תמונות אמינות למדי של דבר מה רציף - למשל, שדה חמניות - תוך שימוש במספר קטן של תמונות בסיס), אבל עיקר העניין בהם הוא תיאורטי. השאלה הבסיסית היא פשוטה והגיונית - נתונה לך קבוצה של אריחי וונג. האם בכלל קיים ריצוף שמשתמש בהם, או שכל נסיון לריצוף יוביל למשהו לא חוקי?

כשמדובר על קבוצה סופית של אריחים (ולכן גם על ריצוף של שטח סופי) הבעיה פתירה תמיד, למרות שהפתרון אינו בהכרח יעיל; נעזוב את זה לעת עתה. את המקרים של קבוצה אינסופית שמנסה לרצף שטח אינסופי אפשר להפריד לשניים - קבוצה שמכילה אינסוף סוגים שונים של אריחים, וקבוצה שמכילה אמנם אינסוף אריחים, אבל מתוך קבוצה סופית של סוגים. בפרט אפשר לדבר על מצב שבו יש לנו מספר אינסופי של עותקים מכל סוג של אריח שבקבוצה.

אם תשימו לב, ביצעתי שני צמצומים רציניים של הבעיה בפסקה האחרונה. הסיבה לכך היא שכבר הבעיה המצומצמת הזו היא בלתי כריעה. לא קיים אלגוריתם שמקבל קבוצה סופית של אריחי וונג ואומר האם ניתן לרצף את המישור כולו באמצעות אינסוף עותקים שלה, ולכן גם לא קיים אלגוריתם לבעיות הרחבות יותר (למה?)

צריך לבצע כאן הסתייגות פשוטה אחת - כאשר עוסקים באינסוף עותקים של אריחים מסוגים שונים, חייבים להוסיף מגבלה נוספת - שאסור יהיה לסובב את האריחים. הסיבה לכך פשוטה - אם היה מותר לסובב, אפשר היה לרצף את כל המישור באמצעות אינסוף עותקים של אריח בודד כלשהו! נסו לעשות זאת באמצעות אחד מהאריחים שבתמונה (בחרו אריח “כללי” - כזה שכל ארבעת הצבעים שעליו שונים - ונסו להגיע לצורה מחזורית כלשהי - כזו שיכולה להתחבר לעצמה מכל אחד מהצדדים).

הסיבה שבגללה העליתי את כל הנושא הזה היא ההוכחה. את המקרה הכללי לא אוכיח, כי ההוכחה מסובכת יחסית, ולכן אתמקד במקרה פרטי, שבו ההוכחה היא ישירה למדי וקל להתמקד ברעיון היפהפה שמאחוריה. המקרה הפרטי הוא זה שבו אנו שואלים רק האם ניתן לרצף רבע מישור (נניח, הרבע הימני העליון), כאשר המשבצת בפינה השמאלית התחתונה של המישור נתונה מראש.

המגבלה של “רבע מישור” היא זניחה. ברור לחלוטין שאם אפשר לרצף את כל המישור, אפשר לרצף רבע מישור. ההפך פחות ברור, אך ניתן להוכחה ללא קשיים ניכרים; ההוכחה הסטנדרטית משתמשת במה שמכונה “למת האינסוף של קניג”, ואשאיר זאת כאתגר לקורא לחשוב על הוכחה. אולי אציג בהמשך הוכחה יותר ישירה (למרות שבבסיסה היא זהה להוכחה הסטנדרטית), בד בבד עם הצגת ההוכחה של משפט הקומפקטיות עבור תחשיב הפסוקים בלוגיקה, פשוט מכיוון ששתי ההוכחות הן בעצם אותו הדבר.

לעומת זאת, המגבלה של “המשבצת השמאלית התחתונה נתונה מראש” היא כבר יותר מהותית. פחות חשובה הדרישה על המיקום המדוייק של המשבצת - מספיק לדרוש שאריח וונג מסויים ששייך לקבוצה ישתתף בריצוף. כאן אני נתקע: אשמח לשמוע על מישהו (או מישהי) שרואה דרך לבצע רדוקציה מהבעיה הזו לבעיה המקורית - כלומר, בהינתן שקיים אלגוריתם שבודק האם רבע המישור ניתן לריצוף בידי קבוצה כלשהי של אריחים, המישהו (או המישהי) יצליח לבנות אלגוריתם שבודק האם רבע המישור ניתן לריצוף בידי קבוצת אריחים, ובהכרח איבר מסויים מתוכה (שזהותו גם כן נתונה כקלט) משתתף בריצוף.

אם כן, נעסוק מכאן והלאה רק בבעיית “רבע מישור, משבצת ראשונה נתונה”. למה ההוכחה שהבעיה הזו אי כריעה היא כל כך יפה? כי מה שמבצעים בה הוא סימולציה ישירה של מכונת טיורינג. כך הופך באחת משחק הריצוף התמים למודל חישובי, וכך נוצר קשר בין שני דברים שעל פניו הקשר ביניהם הוא רופף במקרה הטוב - ומציאת קשרים כאלו, לטעמי, היא התבלין המרכזי שהופך את המתמטיקה לטעימה כל כך.