לצאת מהמשולש

והיום - חידה ופתרונה. כתמיד, מומלץ קודם כל לנסות לפתור את החידה, אפילו לשבור עליה את הראש, ורק לאחר מכן להביט בפתרון. רק “אספיילר” (ואזהיר) מראש שה”פתרון” המדויק הראשון שמצאתי לחידה היה “זו רמאות!”

והנה החידה:

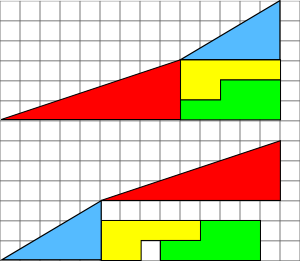
בזכות נייר המשבצות (האחיד, לא צריך לבדוק) קל לראות שארבע הצורות (האדומה, הכחולה, הירוקה והצהובה) זהות בין שני הציורים. אם כן, מאיפה צץ הריבוע הריק שבציור התחתון?

זו החידה.

עכשיו לפתרון (לא לקרוא הלאה אם לא פתרתם!)

למעשה, החידה הזו בכלל אינה חידה מתמטית (טוב, היא קצת מתמטית, במובן זה שמי שבעל נסיון במתמטיקה אולי יצליח לעלות על הרמאות יותר בקלות). זו אשליה אופטית - עוד אחד מהמקרים שבהם העיניים שלנו משדרות משהו למוח, והוא “מתקן” אותו בצורה שגויה. במקרה שלנו, המוח בוחר לראות קו עקום בתור קו ישר (אולי לא אצל כולכם, כמובן).

מקור התמיהה שהחידה מעוררת בתחושה שבשני הציורים אנחנו רואים משולש, ואת אותו משולש - ועם זאת, אנחנו רואים ש”נוספה” לו משבצת איכשהו, ולא מצליחים להבין איפה היא התחבאה עד עכשיו. התשובה העגומה היא שאין כאן בנך-טרסקי חדש: אנחנו פשוט לא רואים את אותה הצורה, והצורה היא בכלל לא משולש; היא מרובע. ה”אלכסון” של המשולש מורכב משני קווים בעלי שיפועים שונים.

שיפוע של ישר בא לציין עד כמה הוא רחוק מלהיות אופקי. הדרך הבסיסית לחשוב עליו היא כזו: אם השיפוע של ישר הוא המספר m, אז כשאנחנו הולכים יחידה אחת ימינה על ציר ה-x, הגובה של הישר גדל ב-m. כך, ישר עם שיפוע 0 יהיה אופקי (לא יעלה בכלל), ישר עם שיפוע 1 יהיה סימטרי ביחס לשני הצירים, וכן הלאה. לישרים אנכיים כל הדיון הזה לא תקף; אם הולכים קצת על ציר ה-x, כבר לא נמצאים על הישר. מטעמי נוחות קוראים לשיפוע כזה “אינסופי” (כמובן, יש אינטואיציה מאחורי השם - ככל שישר קרוב יותר להיות מאונך, כך השיפוע שלו גדול יותר ויותר בערכו המוחלט).

במשולש ישר זווית שמקביל לצירים קל לבדוק מה השיפוע של היתר (הצלע האלכסונית, זו שמול הזווית הישרה): פשוט מחלקים את גובה המשולש באורך הבסיס שלו (למה?). מהתמונה ברור ששיפוע המשולש הכחול הוא 2/5, ואילו שיפוע המשולש האדום הוא 3/8 - ושני אלו אינם אותו מספר. אם כן, היתר של המשולש הכחול לא מתחבר ליתר של המשולש האדום בצורה נחמדה ויוצר קו אחד - יש שני קווים, שמתחברים זה לזה בצורות שונות בכל אחד משני הציורים, וזה מה שגורם לתופעה המוזרה שבחידה.

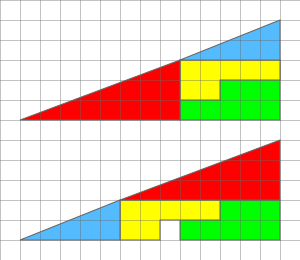
הדרך הפשוטה ביותר לראות זאת היא על ידי הקצנה. לקחתי את התמונה המקורית ומתחתי כל אחד משני המשולשים כך שהבדל השיפועים שלהם יהיה גדול הרבה יותר - של הכחול הפך להיות 3/5, ושל האדום הפך להיות 3/9 (או בעשרוני: 0.6 אל מול 0.333). כתוצאה מכך “הרווחתי” המוני משבצות, וההבדל ברור - היצור המורכב כבר לא נראה כמו משולש, ומובן מאליו שאלו שני יצורים שונים בכל אחד משני הסידורים:

אינטואיטיבית, אפשר לומר שהצורה הראשונה מכילה “שקע” והשניה מכילה “בליטה” על גבי הקו שאמור לכאורה להיות היתר של המשולש הגדול שמורכב מכל הצורות. כעת ברור לגמרי שה”יתר” אינו קו ישר אלא קו שבור, ושכוחה של החידה המקורית באשלייה שהקו ישר. בלשון קצת יותר פורמלית, הצורה השנייה היא קמורה בעוד שהצורה הראשונה אינה קמורה. המילה “קמורה”, בהקשר של צורות גאומטריות, פירושה “עבור כל שתי נקודות בתוך הצורה, גם הקו הישר שמחבר ביניהן נמצא בתוך הצורה”. עבור הצורה השניה (אם מחשיבים גם את המשבצות ה”ריקות” שבפנים כחלק מהצורה) לא קשה לראות שהיא קמורה, ואילו הצורה הראשונה לא קמורה - למשל, הקו שמחבר את הקודקוד העליון של המשולש הכחול ואת הקודקוד השמאלי של המשולש האדום לא עובר בתוך הצורה. לכן בצורה הלא קמורה, הרבה מהשטח “נזרק החוצה”, בזמן שבצורה הקמורה הרבה מהשטח דווקא נכנס פנימה, ואז אפשר להציג אותו בתור משבצת לבנה שצצה יש מאין.

ושוב - מה לזה ולמתמטיקה? נראה לי שהלקח המתמטי החשוב ביותר כאן הוא שדרך פשוטה להתמודד עם תוצאות שנראות לא הגיוניות הוא לנסות עוד מקרים, בפרט מקרים קיצוניים, כדי לגלות את התכונה הבסיסית המשותפת להן. עוד לקח חשוב, שמרצים למתמטיקה מנסים להנחיל לסטודנטים כבר מיומם הראשון באוניברסיטה, הוא שאסור להוכיח דברים באמצעות ציור!