עיניים כחולות

מי מכם שטרם יצא להם להכיר את קומיקס הרשת xkcd, אני ממליץ עליו בחום (למעשה, לא ברור לי מדוע עד עתה לא שמתי אותו בבלוגרול שלי). לא רק שזהו אחד מהקומיקסים היחידים ש(לפעמים) עוסק בצורה הכי ישירה שאפשר במתמטיקה, מדעי המחשב ופיזיקה (ועושה את זה בצורה לא מתנחמדת, שללא ספק תפספס חלק נכבד מהקוראים שפשוט לא יבינו על מה הוא מדבר), הוא גם מצליח להיות קולע במגוון נושאים אחרים, מתרבות האינטרנט ועד למערכות יחסים. רנדל מונרו, כותב הקומיקס, הוא ללא ספק בחור מוכשר ביותר. הנה מספר דוגמיות שאהובות עלי במיוחד:

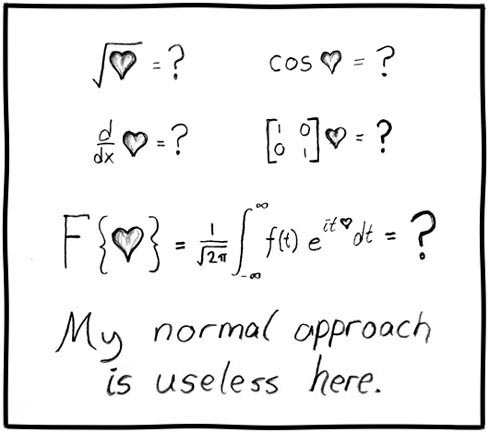
אלו רק דוגמיות; אני ממליץ לכל קורא של הבלוג הזה להיכנס לקומיקס ולקרוא כמה שיותר ממנו. מילת אזהרה אחת: לכל קומיקס יש גם “סבטקסט” - טקסט (שבאופן טכני, אמור לשמש כתחליף לתמונה בדפדפנים שלא מציגים תמונות) שלרוב נלווה לקומיקס ומשלים אותו (או סתם מבלבל עוד יותר). אפשר לראות אותו (בדפדפנים מסויימים) על ידי החזקת סמן העכבר מעל התמונה ללא תזוזה למספר שניות, או על ידי בחירת Properties מהתפריט הימני שנפתח כשלוחצים על התמונה.

וכעת לעניין שלשמו התכנסנו - חידה שרנדל מונרו הציג בבלוג שלו (לא בקומיקס עצמו): “עיניים כחולות”. ולמה הפלגתי קודם בתשבוחות למונרו? כי אני סבור שבכל הנוגע לחידה הזו, הוא מגזים בצורה פראית: הוא מכנה אותה בשם “The Hardest Logical Puzzle in the World”, לא פחות. לדעתי מדובר בחידה קלה למדי, אף שכמובן אני סובייקטיבי. הנה החידה, בניסוח מקוצר שלי: יש לנו אי מלא באנשים, כך שאף אחד מהם לא יודע את צבע העיניים שלו (ואין לו שום דרך לברר - אין מראות וכו’)  אבל כן יודע את צבע העיניים של כל היתר. אם זה מזכיר לכם משהו, זה לא במקרה: כבר עסקתי כאן בחידה שבה לכל אדם היה כובע בצבע שאותו הוא לא ראה, אבל הוא כן ראה את צבע הכובע של שאר האנשים.

כאן מה שקורה הוא קצת שונה. הכלל הוא כזה: כל לילה בחצות באה מעבורת אל האי. כל מי שיודע בודאות (לוגית) מה צבע העיניים שלו עצמו, עוזב. היתר נשארים. כמובן שהשאלה המיידית היא “איך לעזאזל מישהו יכול לדעת מה צבע העיניים שלו עצמו”, ולכן כאן מוכנס הטוויסט. יש באי 100 אנשים כחולי עיניים, 100 אנשים עם עיניים חומות, ועוד אדם אחד בעל עיניים ירוקות - “הגורו”. יום אחד בצהריים הגורו פוצח את פיו ואומר “אני רואה מישהו עם עיניים כחולות”. זהו. זה כל המידע שהאנשים מחליפים ביניהם. פרט לכך, אין שום תקשורת. מה שכן מניחים הוא שכל האנשים על האי הם “לוגיקאים מושלמים”, כלומר שאם יש מסקנה שאפשר להגיע אליה בצורה לוגית, הם יעשו זאת.

השאלה שנשאלת כעת היא “מי יעזוב את האי, ומתי?”

מכיוון שאני עומד להציג את הפתרון (ולדון בו) בפוסט הזה, אני ממליץ לכל מי שהחידה מעניינת אותו (וזו אכן חידה מעניינת) לחשוב עליה זמן מה לבד לפני שיקרא את הפתרון. לבינתיים, הנה הפסקת ביניים שמלווה בעוד כמה קומיקסים:

וכעת - לפתרון. התשובה היא שבלילה ה-100 יעזבו 100 בעלי העיניים הכחולות את האי. איך לעזאזל מגיעים לתשובה הזו?

כמו תמיד בחידות שבהן יש מסכי עשן מבהילים בדמות המספר 100, כדאי להתחיל מהמקרים הפשוטים ביותר שאפשר לחשוב עליהם. ברור שאנחנו רוצים לשמר את הסימטריה בין בעלי העיניים הכחולות והחומות ושהמקרה שבו הגורו לבד באי הוא חסר טעם, ולכן מתחילים מלחשוב על המקרה שבו יש כחול עיניים אחד וחום עיניים אחד. המקרה הזה פשוט למדי, ואפשר להבין תכף ומייד מה יקרה בו: בעל העיניים הכחולות יעזוב את האי כבר בלילה הראשון. למה? כי הוא רואה שפרט לגורו, האדם האחר באי הוא בעל עיניים חומות. כלומר, ברור לו שהגורו דיבר עליו, ולכן יש לו עיניים כחולות. האיש בעל העיניים החומות, לעומת זאת, לא יכול לעזוב; הוא רואה את האיש בעל העיניים הכחולות וחושב “הממ, אולי הגורו דיבר עליו ולא עלי” (מה שאכן נכון). למחרת האיש בעל העיניים הכחולות עוזב, מה ש”מאושש” את המחשבה שלו; וחוץ מזה, אולי יש לו עיניים ירוקות כמו הגורו? בקיצור, אין לו שום סיכוי לעזוב.

נעבור כעת למקרה המורכב יותר של שני אנשים בעלי עיניים כחולות ושניים בעלי עיניים חומות. כאן כל בעל עיניים כחולות סובל בדיוק מהבעיה של “אולי הגורו דיברה על השני?” ולכן לא יעזוב בלילה הראשון. אבל כאן מתווספת לכל אדם אינפורמציה: האינפורמציה של “אף אחד לא עזב בלילה הראשון”. כשמחברים אותה לאינפורמציה של “כולם לוגיקאים מושלמים”, אפשר להסיק מסקנה חדשה. ההגיון הוא כזה:

נניח שהיה רק אדם אחד בעל עיניים כחולות על האי. אז כבר בלילה הראשון הוא היה עוזב, מאותן סיבות שראינו במקרה הקודם - לכל האנשים שהוא רואה אין עיניים כחולות, ולכן בעל העיניים הכחולות חייב להיות הוא. מכיוון שאף אחד לא עזב בלילה הראשון, המסקנה היא שיש לפחות שני בעלי עיניים כחולות. כעת, כל בעל עיניים כחולות מסתכל סביבו ורואה שיש רק אדם אחד בעל עיניים כחולות; מכאן שהוא חייב להיות האדם הנוסף בעל העיניים הכחולות. כלומר, בלילה השני יעזבו את האי שני בעלי העיניים הכחולות, ובא לציון גואל.

מכאן קל כבר לבצע קפיצה מחשבתית ו”לנחש” שגם במקרה של ה-100 אנשים בעלי עיניים כחולות, כולם יעזבו את האי בלילה ה-100. הדרך להוכיח זאת, לכל מספר של כחולי עיניים, היא באינדוקציה על מספר כחולי העיניים (שימו לב שמספר חומי העיניים לא משנה כלום). אגב, זו לדעתי דוגמה נאה מאוד לשימוש “יפה” באינדוקציה; חבל לי שבבית הספר מתעקשים להוכיח אי שוויונות באמצעותה ולא מראים אף פעם דוגמה יותר “מתמטית” כמו זו.

כבר ראינו את בסיס האינדוקציה - כלומר, שבהינתן כחול עיניים אחד הוא עוזב ביום הראשון - ונותר להראות את צעד האינדוקציה. אם כן, נניח שאם יש \( n \) כחולי עיניים על האי, הם עוזבים בסוף היום ה-\( n \). כעת נעסוק במקרה שבו יש \( n+1 \) כחולי עיניים באי. כל כחול עיניים רואה \( n \) כחולי עיניים, ואומר לעצמו “אם אני לא כחול עיניים אז יש רק \( n \) כחולי עיניים באי, ולכן ביום ה-\( n \) כולם יסתלקו” (כשהחלק האחרון של דבריו נובע מהנחת האינדוקציה). אם זה לא קורה, נובע מכך שגם מי שאמר זאת לעצמו הוא כחול עיניים, ולכן הוא יעזוב ביום ה-\( n+1 \) - וזה יקרה לכל כחולי העיניים. במה הם נבדלים מבעלי עיניים בצבע אחר? שמי שיש לו עיניים בצבע אחר רואה \( n+1 \) כחולי עיניים מראש, ולכן אם בלילה ה-\( n \) אף אחד לא עוזב, זה עדיין לא אומר לו כלום.

ובכן, זהו סופה של החידה, אבל רנדל לא מסיים כאן. בעמוד שבו הוא מציג את הפתרון שלו (שהוא בבסיסו אותו הפתרון כמו זה שאני מציג כאן) הוא שואל שאלות נוספות על החידה, ובפרט את השאלה שהיא די מעניינת, לטעמי, גם עבור מי שהסכים “באופן פורמלי” עם הפתרון - מה המידע שהגורו נותן לשאר האנשים, שהם לא ידעו כבר קודם?

אם יש רק בעל עיניים כחולות אחד, ברור שהגורו נתן לו מידע. עם זאת, כשיש שני בעלי עיניים כחולות, לכאורה לא נוסף שום מידע חדש: כל אחד יודע שיש מישהו עם עיניים כחולות. ובכל זאת, בלי הגורו הם לא היו מצליחים לעשות כלום. איך זה ייתכן?

הרעיון כאן הוא שכל בעל עיניים כחולות משחק בראש משחק של “מה היה קורה אילו”. הוא שואל את עצמו “מה היה קורה אם לא היו לי עיניים כחולות?”. במקרה של שני בעלי עיניים כחולות, זה פשוט; אם לאחד מהם לא היו עיניים כחולות, אז היה רק שחקן אחד עם עיניים כחולות ואז בוודאי שהגורו מעביר מידע. דווקא בגלל שהמידע הזה לא מנוצל מיידית, אפשר להסיק ממנו, בטווח הארוך, מידע חדש (שיש שני אנשים עם עיניים כחולות).

כשמגיעים לשלושה בעלי עיניים כחולות עוד יותר קשה לראות מה הולך שם. הרי כאן המשחק שכל אחד משחק עם עצמו הוא “נניח שבאמת יש רק שני בעלי עיניים כחולות” - וכאמור, על פניו הגורו לא מוסיף להם מידע; אבל בתוך משחק ה”נדמה לי” הזה יש משחק “נדמה לי” פנימי יותר (בדיוק זה של הנחת האינדוקציה), שמראה שכן ניתן להפיק מידע ממה שהגורו אמר. הסיבה לכך ש”נדמה לי” פנימי שכזה הוא אפשרי בכלל היא שאמנם, בעל העיניים הכחולות שלנו מדמיין מה קורה לשני בעלי עיניים כחולות אחרים; אבל כשהוא מדמיין מה כל אחד מהם חושב, הוא מביא בחשבון את זה שהם לא רואים את עצמם ולא יודעים שיש להם עיניים כחולות - רק הוא, כצופה חיצוני, יודע זאת.

מבלבל? אוהו. פתאום החידה הפשוטה מתגלה כמאתגרת יחסית. עם זאת, אני לא חושב שיש כאן סיבוך כלשהו מבחינה מתמטית; פשוט קשה לעקוב אחרי השתלשלות החשיבה הזו כפי שקשה לעקוב אחרי ריצת רקורסיה.

לסיום, רק הערה אחת: שימו לב שהכנסת האנשים בעלי העיניים החומות למשחק היא סתם מסך עשן שבא לבלבל. אין בהם כל צורך ממשי וניתן לספר את החידה גם בלעדיהם - ובכל זאת, לא השמטתי אותם כי לא רציתי להתרחק יותר מדי מהגרסה של רנדל. מה שכן, כאשר מסלקים את חומי העיניים מקבלים ניסוח שונה למדי ונפוץ הרבה יותר של החידה, שוביניסטי וגס הרבה יותר. כדי להפחית במקצת את השוביניסטיות אהפוך את התפקידים: בכפר מסויים גרות 3 נשים נשואות (שוב, 3 הוא מספר שרירותי). אם אישה מגלה שבעלה בגד בה, היא יורה בו (פעם אחת) באותו הלילה. ידוע לנו, כצופים מבחוץ, שכל הגברים בוגדים בנשותיהם, וכל אישה יודעת על כל הבגידות חוץ מאשר על הבגידה של בעלה בה. יום אחד שומעות שלוש הנשים (מה”גורו”, אולי?) שבעלה של אחת מהן בוגד בה. באיזה לילה יישמעו יריות, וכמה?