למה (בגדול, מאוד בגדול) לא ניתן לפתור משוואות ממעלה חמישית ומעלה, ומה זה בכלל אומר?

אחת מהצורות הפופולריות שבהן נתפסת המתמטיקה בציבור הרחב היא בתור העיסוק ב”פתרון משוואות”. כמובן שזה תיאור מקומם של המתמטיקה, ואני מקווה שכבר סיפקתי בעבר דוגמאות אין ספור לכך שהמתמטיקה היא הרבה יותר מסתם עיסוק ב”פתרון משוואות”, אך הפעם אני רוצה לדבר בדיוק על זה - משוואות. מהסוג שנלמד בבית הספר. אז בואו נתחיל מההתחלה.

משוואות יכולות לדבר על הרבה אובייקטים מתמטים (למשל, בתחום של משווואות דיפרנציאליות, האובייקט הוא פונקציות) אבל אנחנו נצטמצם לדיבור על משוואות במספרים. \( 1+1=2 \) היא דוגמה למשוואה - מימין ומשמאל לסימן השווה (במה שנקרא “אגף ימין” ו”אגף שמאל”) נמצא אותו ערך, כשהוא מתואר בשתי דרכים שונות. משוואה כמו \( 1+1=2 \) היא פשוטה יחסית (כן, אני מודע לכך שאפשר לכתוב עליה פוסט בפני עצמו), אבל לפעמים המשוואות מספקות יותר אינפורמציה, למשל \( 0.999\dots=1 \) שכבר עסקתי בה. אלא שבדרך כלל כשעוסקים במשוואות, מכניסים לתמונה נעלמים, וכאן העסק מתחיל להסתבך.

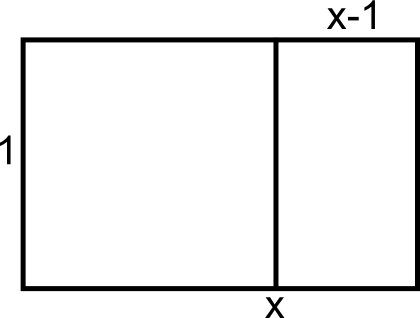
בואו נדבר לרגע על בעיה מה”עולם האמיתי”. יש לנו דף נייר שרוחבו הוא 1. אנחנו רוצים לדעת מה צריך להיות אורכו של הנייר כדי שיקיים את התכונה החביבה הבאה: אם מחלקים את הנייר לריבוע ומלבן, המלבן החדש הוא בעל אותן פרופורציות בין אורך לרוחב כמו אלו של דף הנייר המקורי.

איך פותרים את הבעיה הזו? ראשית, מסמנים את אורכו של הנייר ב-\( x \). זה מציין שאורך הנייר הוא “נעלם” - ערך מספרי כלשהו שכרגע אין לנו מושג מה הוא (או אפילו אם באמת קיים כזה, או אם הוא יחיד או שיש כמה אורכים שמקיימים את אותה תכונה). כעת אנחנו רוצים לכתוב משוואה כלשהי ש-\( x \) מופיע בתוכה, בתקווה שאפשר יהיה להמיר אותה במשוואה אחרת שנותנת לנו את ערכו של \( x \). מה יש בניסוח הבעיה המקורית שיש בו שווין? השוויון של הפרופורציות של המלבן החדש עם המלבן הישן. הפרופורציה במלבן הישן היא \( \frac{x}{1} \); הפרופורציה במלבן החדש היא \( \frac{1}{x-1} \), ולכן ניתן לכתוב \( \frac{x}{1}=\frac{1}{x-1} \). כעת מתחילים לבצע על המשוואה מניפולציות; הרי אם \( 1+1=2 \) אז גם \( 1+1+3=2+3 \), כלומר אפשר לחבר את אותו ערך לשני האגפים גם יחד ולקבל משוואה חדשה שגם היא נכונה; ובאופן דומה ניתן גם לחסר, לכפול ולחלק. בכל הנוגע לכפל וחלוקה צריך להיזהר קצת - אסור לחלק באפס, ואם “מרמים” ומרשים חלוקה באפס יכולים לקבל משוואות שגויות (דרך מאוד פופולרית להוכיח ש-\( 1=2 \) מתבססת על חלוקה מובלעת באפס). במקרה שלנו אין צורך לחלק באפס, אם כי הייתה יכולה להיות סכנה בביטוי \( \frac{1}{x-1} \) אם \( x \) היה שווה אחד; אבל בגלל ש-\( x \) הוא אורך מלבן (שאינו ריבוע) שרוחבו \( 1 \) והאורך תמיד גדול מהרוחב (זו ההגדרה…) אז \( x>1 \) ואין כאן בעיה.

אז מה שעושים הוא לכפול את שני אגפי המשוואה ב-\( x-1 \) ולקבל \( x\left(x-1\right)=1 \). פותחים את הסוגריים באגף שמאל ומקבלים \( x^{2}-x=1 \). מחסירים 1 משני האגפים ומקבלים \( x^{2}-x-1=0 \). הגענו ל”צורה קנונית” של משוואה ממעלה שניה. איך פותרים דבר כזה? התשובה הייתה ידועה כבר לבבלים והצגתי את הרעיון בפוסט קודם - את הפתרונות של המשוואה \( ax^{2}+bx+c=0 \) ניתן למצוא בעזרת המשוואה \( x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \). המשוואה הזו היא קצת “רמאות” - יש בה את ה-\( \pm \), שמשמעותו שבעצם יש כאן שתי משוואות שזהות זו לזו פרט לכך שבאחת כתוב שם פלוס ובשניה מינוס; ופרט לכך יש שאלה של מה קורה אם \( b^{2}-4ac \) אינו חיובי, אך לא ניכנס לכך כעת. במקרה שלנו, הצבת הערכים נותנת את הפתרונות \( \frac{1\pm\sqrt{5}}{2} \), ומכיוון שאנחנו יודעים שמתקיים \( x>1 \) אז נובע שהפתרון לבעיה המקורית הוא הקבוע שנקרא “יחס הזהב”: \( \phi=\frac{1+\sqrt{5}}{2} \).

טוב, אז עכשיו אפשר לדבר באופן כללי על “משוואות ממעלה \( n \)”. אלו משוואות שבהן מופיע \( x \) וחזקות שלו, כשכל מופע של \( x \) מוכפל במספר כלשהו - “מקדם”. מכיוון שנוח לדבר על החזקה ה-0 של מספר בתור 1 (\( x^{0}=1 \)), ההגדרה הזו תופסת גם מספרים שאינם צמודים למופע של \( x \), כמו ה-\( c \) במשוואה שלעיל (שאפשר לחשוב עליו כעל \( c\cdot x^{0} \)). ההגדרה אינה פורמלית עד הסוף - למשל, ראינו שהמשוואה \( \frac{x}{1}=\frac{1}{x-1} \) היא בעצם משוואה ממעלה שניה בתחפושת, אך באופן ההצגה הזה שלה היא אינה עונה על ההגדרה - אבל די בכך עבורנו. השאלה שאנחנו מצטמצמים אליה ב”פתרון משוואות”, אם כן, היא זו: בהינתן משוואה מהצורה \( a_{n}x^{n}+a_{n-1}x^{n-1}+\dots+a_{1}x+a_{0}=0 \), מהם הערכים של \( x \) שפותרים אותה?

משוואה ממעלה ראשונה היא קלה: פתרון \( ax+b=0 \) הוא פשוט \( x=-\frac{b}{a} \) (צריך ש-\( a \) יהיה שונה מאפס, אבל אם הוא אפס זו לא באמת משוואה ממעלה ראשונה; ובאופן כללי מניחים תמיד שהמקדם של החזקה הגבוהה ביותר אינו אפס). במקרה הזה יש פתרון יחיד. על משוואה ממעלה שניה כבר דיברנו. ומה הלאה? גם עבור משוואות ממעלה שלישית ורביעית יש נוסחה לשורשים, אלא שאין לי שום כוונה להציג אותה כאן לכו והביטו בה בויקיפדיה ותבינו מדוע. מדובר בנוסחאות ענקיות ומזוויעות. אם מנסים לכתוב את הכל “בבת אחת” על הדף, חושכות העיניים. מה כן אפשר לעשות? לפרק את חישוב הפתרונות לכמה שלבי ביניים - סדרה של משוואות שמגדירות ערכי ביניים, ואז המשוואה הסופית אינה נוראית כל כך. אפשר להדגים זאת גם על משוואות ממעלה שניה: לפעמים נהוג להשתמש בסימון \( \Delta=b^{2}-4ac \) (שנקרא “הדיסקרימיננטה של המשוואה”), ואז הפתרון הכללי של המשוואה הוא \( \frac{-b\pm\sqrt{\Delta}}{2a} \) - קצת יותר פשוט.

זה מצביע על כך שנוסחה היא בעצם גרסה פשוטה של אלגוריתם. אוסף של פעולות חישוביות שנותנות בסופו של דבר את התשובה הנכונה. במקרה הזה האלגוריתם מקבל כקלט את מקדמי המשוואה, והפלט שלו הוא אחד מהערכים האפשריים של פתרון המשוואה. למשל, עבור משוואה ממעלה ראשונה האלגוריתם הוא “קח את המקדם \( b \), חלק אותו ב-\( a \), הכפל את הכל במינוס 1 וסיימת”. האלגוריתם הזה מתבסס על כך שאנחנו יודעים לבצע פעולות מסויימות - בפרט, לבצע חלוקה (שהיא לא דבר מובן מאליו כלל). האלגוריתם של פתרון משוואה ממעלה שניה מעלה קצת את רמת התחכום - צריך לבצע חיבור או חיסור, צריך לכפול ב-2 (את המקדם \( a \)), והכי חשוב - צריך להוציא שורש ריבועי, כשמחשבים את \( \sqrt{\Delta} \). חישוב שורש ריבועי אינו עסק טריוויאלי (אם כי גם לא נורא במיוחד - הרחבתי על כך בעבר). קל לראות שהפעולה של “הוצאת שורש” היא הכרחית - למשוואה \( x^{2}-2=0 \) לא ניתן למצוא פתרון שמתקבל רק מפעולות של חיבור, חיסור כפל וחילוק על מקדמי המשוואה (שהם \( 1 \) ו-\( -2 \)) שכן פעולות אלו יחזירו רק מספרים רציונליים, ופתרונות המשוואה (\( \sqrt{2} \) ו-\( -\sqrt{2} \)) אינם מספרים רציונליים.

הנוסחאות לפתרון משוואות ממעלה שלישית ורביעית הן מסובכות נורא, אבל הן מתוות אלגוריתם שמשתמש פחות או יותר באותן פעולות - חיבור, חיסור, כפל, חילוק והוצאת שורש. ההבדל היחיד הוא שהוצאת השורש יכולה להיות מסדר כלשהו, לא רק שורש ריבועי. עבור משוואה ממעלה שלישית צריך הוצאת שורש מסדר 3 (כלומר, בהינתן \( a \) למצוא מספר \( b \) שמקיים \( b^{3}=a \)), ועבור משוואה ממעלה רביעית צריך הוצאת שורש מסדר 4.

כעת הגענו לנקודה המרכזית, החשובה ביותר בכל הפוסט - כשאומרים ש”אין נוסחה לפתרון משוואה מעלה חמישית ומעלה”, למה מתכוונים? לכך שלא קיימת נוסחה שהמרכיבים שלה הם רק פעולות חיבור, חיסור, כפל, חילוק והוצאת שורש מסדר כלשהו. על משוואה שכן ניתן לכתוב לה פתרון באופן הזה אומרים שניתן לפתור אותה “באמצעות רדיקלים”. יש משוואות, גם ממעלה חמישית, שניתנות לפתרון באמצעות רדיקלים (דומה קיצונית היא משפחת המשוואות \( x^{5}-a=0 \) שפתרונן הוא פשוט \( a^{\frac{1}{5}} \), כלומר הוצאת שורש חמישי של \( a \)); פשוט לא ניתן לעשות זאת לכל המשוואות. זה לא אומר שלא קיים למשוואות הללו פתרון - קיים. זה לא אומר שלא ניתן לחשב אותו - ניתן. זה פשוט אומר שהאלגוריתם שבאמצעותו נחשב את הפתרון הוא יותר מורכב מהאלגוריתמים שבעזרתם פתרנו משוואות ממעלה נמוכה יותר. לא שאני מזלזל בתוצאה הזו או ביופי שלה - על פניו, אין שום סיבה מדוע יהיה שינוי דרסטי כזה בין משוואה ממעלה רביעית לחמישית; הגיוני היה להניח שמה שעבד עד כה ימשיך לעבוד ושנוסחה לפתרון משוואה ממעלה חמישית (שתהיה ארוכה ומפלצתית) תתגלה. היסטורית, המתמטיקאים אכן שברו את הראש על הבעיה הזו במשך מאות שנים; לבסוף, במאה ה-19, הגיע אבל והוכיח שאין פתרון כללי למשוואה ממעלה חמישית; ולאחר מכן הגיע גלואה וניסח תורה כללית יותר שבאמצעותה ניתן גם להבין בדיוק מתי למשוואה יהיה פתרון באמצעות רדיקלים ומתי לא. זו התורה הזו - תורת גלואה - שעליה ארצה לדבר בהמשך. חשוב להבהיר שתורת גלואה היא מרחיקת לכת הרבה יותר מאשר פתרון בעיית המשוואות הנ”ל - כבר תיארתי בעבר את בעית בניית המצולעים המשוכללים באמצעות סרגל ומחוגה, וזו בעיה נוספת שתורת גלואה חיסלה לגמרי. בימינו לא ניתן למצוא כמעט טקסט העוסק באלגברה מודרנית שלא משתמש כל הזמן ברעיונות מתורת גלואה - היא הפכה להיות חלק מהלחם והחמאה של המתמטיקה, בדומה לחשבון האינפיניטסימלי.

על קצה המזלג, אנסה להסביר עכשיו איך בכלל מוכיחים את הדבר הזה. פירוט יבוא (אני מקווה) בפוסטים עתידיים.

איני בטוח לגבי הניסוח המקורי של גלואה, ולכן אסתפק בלדבר על הניסוח המודרני, שמשתמש במושגים שלא היו קיימים בצורה מפורשת בזמנו של גלואה (ואין ספק שהרעיונות שלו תרמו תרומה אדירה לעבר יצירתם - בדרך כלל מושג כללי נוצר לאחר שהצטברו מספיק מקרים פרטיים חשובים שמתאימים לו). הרעיון הבסיסי שבתורת גלואה הוא לקשור בין המושג של הרחבת שדות (שעליו דיברתי בפוסטים קודמים), למושג של חבורה. לא אגדיר כרגע את המושגים הללו - רק אעיר ש”שדה” הוא הכללה של אובייקטים כמו המספרים הרציונליים והמספרים הממשיים - קבוצה שסגורה לארבע פעולות החשבון והן מתנהגות בה בצורה ה”רגילה” (למשל, מתקיים \( a+b=b+a \)).

יותר במדוייק - לכל הרחבת שדות מותאמת חבורה - חבורת גלואה של הרחבת השדות - באופן כזה שיש התאמה של אחד לאחד בין המבנה של תתי החבורות של חבורת הגלואה, ותתי השדות של שדה ההרחבה. זה מתקשר לפתרון של משוואות מכיוון שניתן לתאר הרחבת שדות (סופית) בתור “מה שקורה לשדה כשמוסיפים אליו פתרונות של משוואה שמקדמיה נלקחו מתוך השדה הזה”.

כעת, אם משוואה ניתנת לפתרון על ידי רדיקלים, אז אפשר “להגיע אל הפתרון” באמצעות סדרת פעולות חשבון והצאות שורש. הסדרה הזו ניתנת לתרגום לסדרה של הרחבת שדות, החל משדה בסיס שנוצר באמצעות מקדמי המשוואה וכלה בשדה שמכיל את הפתרון. כל הרחבה בסדרה הזו היא פשוטה - נוצרת על ידי הוצאת שורש. לכן קיבלנו בין השדה שהתחלנו ממנו והשדה שסיימנו בו סדרה של תת-שדות שכל אחד מהם מתקבל בצורה פשוטה מקודמו. בחבורת הגלואה המתאימה זה מתורגם לסדרה של תת חבורות בעלות תכונה מסויימת. זה מוביל אותנו להגדרה העיקרית - חבורה היא פתירה אם קיימת בה סדרה של תת חבורות שמקיימת כך וכך (כל אחת מהחבורות בסדרה היא תת חבורה נורמלית של קודמתה, והמנה של כל זוג חבורות עוקבות אבלית). זו הגדרה יחסית קלה שניתן לעבוד איתה, ובפרט להוכיח שחבורות מסויימות לא מקיימות אותה.

השלב הבא הוא לדבר באופן מדוייק על משוואה “כללית” ממעלה \( n \). שוב, לא אכנס כרגע לניתוח, אבל ניתן להגדיר יצור כזה במדוייק ולהוכיח שחבורת הגלואה המתאימה להרחבת השדות על ידי משוואה כזו היא \( S_{n} \) - חבורת הפרמוטציות על \( n \) איברים. ואז מגיע ניתוח מתמטי לא מסובך של החבורות הללו שמראה כי כל עוד \( n\le4 \), אז \( S_{n} \) פתירה; ואילו \( S_{5} \) ומעלה כבר אינן פתירות, מה שמסיים את הסיפור.

ובכן, זה היה מבט מרפרף מאוד על ההוכחה, אך כמובן שהיופי האמיתי טמון בפרטים, שעליהם אני מקווה להרחיב בעתיד.