למה פאי לא שווה 4?

באינטרנט מסתובבת לה לאחרונה הוכחה ישנה נושנה לכך ש”\( \pi=4 \)”, כאשר \( \pi \) (פאי) הוא המספר שמציין את היחס בין היקף מעגל וקוטרו בגאומטריה האוקלידית. ההוכחה הזו קצת לא מסתדרת עם הידע המתמטי הסטנדרטי לפיו \( \pi \) אכן קבוע לכל המעגלים, אבל ערכו בכלל מתחיל ב-\( 3.14\dots \) והוא מספר אי רציונלי, כלומר הספרות שמעבר לנקודה העשרונית מתמשכות עד אינסוף ללא מחזוריות. אז מהי ההוכחה ולמה היא לא נכונה? ראשית, ההוכחה:

אז מה יש לנו כאן? סדרה של עקומים שהאורך של כל אחד מהם הוא ללא ספק 4, והם “שואפים” למעגל. הבעיה היא בדיוק במילה שבמרכאות; אם אנחנו טוענים שהעקומים “שואפים” למעגל, עלינו להסביר באיזה מובן - וחשוב מכך, עלינו להסביר למה מתקיימת כאן תכונה מהותית יותר, שבאופן מילולי ניתן לנסח כ”אם סדרת עקומים “שואפת” לעקום ספציפי אחד, אז סדרת האורכים של העקומים שואפת לאורך של אותו עקום ספציפי”. למעשה, זו תכונה כל כך מהותית שכנראה נרצה להגדיר “שאיפה” באופן שיבטיח שהיא תתקיים. הסיבה שההוכחה היא שגויה היא שסדרת העקומים שנבנית בה לא שואפת להיקף המעגל בשום מובן מתמטי סטנדרטי, ובפרט אין סיבה להניח שמתקיימת התכונה שגבול האורכים של סדרת העקומים יהיה האורך של המעגל. זו ללא ספק התחושה האינטואיטיבית שנוצרת בנו (גם בי) כשאנו מסתכלים על ההוכחה, אבל במתמטיקה אינטואיציות שגויות כאלו שנובעות מהתעסקות באינסוף, או מ”הוכחה באמצעות ציור” הן דבר נפוץ ביותר - כאן יש לנו פשוט עוד דוגמה נאה לאופן שבו אינטואיציה כזו נוצרת.

אז מה עושים המתמטיקאים? לזה אקדיש את עיקר הפוסט. באופן נאיבי יחסית, כדי לחשב אורך של עקום הם בונים לעקום סדרה של קירובים פוליגונליים. קירוב כזה נבנה באופן הבא: מסמנים \( n \) נקודות על העקום, ומותחים קווים ישרים בין הנקודות על פי סדר הופעתן על העקום (מהראשונה אל השנייה, מהשנייה אל השלישית וכדומה). הקווים הישרים הם הדרך הקצרה ביותר לעבור מנקודה אחת לשנייה, כך שהמרחק בין שתי נקודות סמוכות על העקום חוסם מלמעלה את אורך הקו הישר שמחבר את שתי הנקודות. הקירוב הפוליגונלי הוא הקו הישר-למקוטעין שמתקבל מחיבור כל הקטעים הישרים שבנינו; את האורך שלו קל לחשב (זה סכום אורכי הקטעים) והאורך הזה, על פי הטיעון שנתתי, חסום מלמעלה על ידי אורך העקום עצמו. כאשר משאיפים את \( n \) לאינסוף, כלומר מסתכלים על קירובים עם יותר ויותר נקודות על העקום, הקירוב הפוליגונלי שמתקבל הולך ומשתפר.

כעת יש שתי דרכים להגדיר את אורך העקום עצמו - הראשונה היא בתור “המספר הקטן ביותר שגדול או שווה לאורך כל קירוב פוליגונלי אפשרי של העקום” (זהו המושג המתמטי של סופרמום, למי שמכיר), והשנייה היא בתור “הגבול של סדרת האורכים שמתקבלת מסדרת קירובים פוליגונליים שבה \( n \) שואף לאינסוף”. בדרך השנייה צריכים להיות קצת יותר זהירים, שכן הרמאים מביניכם בוודאי כבר חשבו על האפשרות לרכז את כל נקודות הקירוב אי שם בתחילת העקום, מה שמבטיח שרוב הקירוב “יפספס” את העקום - ולכן דורשים דרישה נוספת בהגדרה השניה, והיא שהאורך של כל קטע בקירוב הפוליגונלי צריך לשאוף לאפס. זה מבטיח שגודל ה”טעות” שנוצרת משימוש בקווים ישרים בקירוב ישאף לאפס.

ההגדרה הזו היא, כאמור, נאיבית יחסית; אנסה כעת להציג גישה אחרת שמסתמכת על כלים כבדים מעט יותר ועם זאת נראית אולי קצת יותר “טבעית” ומשכנעת באופן אינטואיטיבי. אזהיר מראש שאני מראה כאן רק את קצה הקרחון; בחשבון אינפיניטסימלי מתקדם עושים את מה שאני אתאר כאן באופן כללי בהרבה, שמאפשר לדבר על דברים נוספים פרט לאורך של עקומים. אבל נעזוב את זה.

איך מודדים מרחק בדרך כלל? ובכן, דרך אחת היא לבוא עם סרגל, אבל זה מתבסס על כך שכבר יש לכם “מרחק מדוד” בכיס, וזו שיטה בעייתית אם אתם רוצים למדוד מרחק גדול ואין לכם סרגל ארוך. אז הנה דרך אחרת: נניח שאתם רוצים למדוד מרחק של מסלול ישר כלשהו. תעמדו בקצה אחד שלו, ובקצה השני תעמידו חבר טוב. סנכרנו את השעונים שלכם, ומתי שמתחשק לכם שלחו גל קול מכם אל החבר. ודאו שלחבר יש גלאי קול רגיש, ושאתם מודדים במדויק את הרגע שבו שלחתם את האות, והרגע שבו החבר קיבל את האות. כעת יש לכם את הזמן שנדרש לאות להגיע מנקודה א’ לנקודה ב’; ואתם גם יודעים את המהירות שבה האות עבר (כן, אני מניח שמהירות הקול קבועה וידועה לכם), אז משני הנתונים הללו ניתן להפיק את המרחק שהאות עבר (הזמן כפול המהירות). זו גם תהיה בדיוק הצורה שבה אנסה להגדיר את האורך של עקום.

שם המשחק פה הוא פרמטריזציה. פרמטריזציה של עקום \( \mathcal{C} \) היא פונקציה \( f:\left[a,b\right]\to\mathcal{C} \) שהיא חד-חד ערכית ועל, ובנוסף לכך גם רציפה, וכך ש-\( f\left(a\right) \) ו-\( f\left(b\right) \) הם שני הקצוות של העקום. אנחנו חושבים על הקטע \( \left[a,b\right] \) בתור מקטע זמן כלשהו, ועל \( f\left(t\right) \) בתור “הנקודה בעקום שבה היינו בזמן \( t \)”. מכיוון שאנו רוצים בסופו של דבר לחשב היקף של מעגל, בואו נעבור לדבר על פרמטריזציות של מעגל היחידה - המעגל שרדיוסו 1 ולכן היקפו \( 2\pi \) (המעגל שב”הוכחה” הוא בעל רדיוס \( \frac{1}{2} \) ולכן היקפו יוצא \( \pi \), אבל יהיה יותר נוח לדבר על מעגל היחידה הרגיל). הדרך הנוחה לתאר את המעגל היא באמצעות הפונקציות הטריגונומטריות: הפרמטריזציה הפשוטה ביותר היא \( f\left(t\right)=\left(\cos t,\sin t\right) \), כאשר \( t\in\left[0,2\pi\right] \). אפשר גם לבחור פרמטריזציה שבה הזמן הוא בין 0 ו-1: \( g\left(t\right)=\left(\cos\left(2\pi t\right),\sin\left(2\pi t\right)\right) \) כאשר \( t\in\left[0,1\right] \). הפונקציה \( g \) מתארת מישהו ש”רץ יותר מהר” על המעגל - אבל כמובן, לוקח לו פחות זמן. אפשר גם לתת פרמטריזציות מופרעות יותר (למשל, מישהו שרץ מהר על החצי הראשון של המעגל, ואז מאט מאוד) אבל נעזוב את זה. כדי לחשב את היקף המעגל די להשתמש בפרמטריזציה אחת כלשהי ולכן בדרך כלל בוחרים את זו שהכי נוחה לנו - כאן זו תהיה \( f \), באופן בלתי מפתיע.

מושג הנגזרת שהצגתי בעבר מתאר היטב את המהירות הרגעית בתנועה במימד אחד. אבל כאן יש לנו תנועה בשני מימדים; איך נתאר אותה? ובכן, באופן כללי אפשר לחשוב על פרמטריזציה כעל שתי פונקציות שונות ש”משחקות יחד” - \( f\left(t\right)=\left(x\left(t\right),y\left(t\right)\right) \) כאשר \( x\left(t\right),y\left(t\right) \) שתיהן פונקציות מ-\( \mathbb{R} \) אל \( \mathbb{R} \), ולכן שתיהן גזירות במובן הרגיל. אם כן, \( \left(x^{\prime}\left(t_{0}\right),y^{\prime}\left(t_{0}\right)\right) \) הוא וקטור שמתאר את רכיבי המהירות של \( f \) בשני הכיוונים - הן בציר \( x \) והן בציר \( y \). כדי למצוא את גודל המהירות משני הרכיבים משתמשים במשפט פיתגורס, ומקבלים שהוא \( \sqrt{x^{\prime}\left(t_{0}\right)^{2}+y^{\prime}\left(t_{0}\right)^{2}} \). למי שכל זה נראה לו כמו ג’יבריש מפחיד - לא נורא; אין הכרח להבין את זה כרגע ובהחלט מספיק הרעיון האינטואיטיבי של “הדרך תחושב באמצעות המהירות והנה הנוסחה שמתארת את המהירות”.

כעת, אם המהירות הרגעית בכל נקודה נתונה לנו, האופן שבו מחשבים את הדרך הכוללת שעברנו הוא באמצעות סכימה של המהירות הרגעית הזו - סכימה מסוג זה נקראת אינטגרל וגם אותה תיארתי כבר בבלוג. נקבל שאורך העקום הוא בדיוק \( \int_{a}^{b}\sqrt{x^{\prime}\left(t\right)^{2}+y^{\prime}\left(t\right)^{2}}dt \). זו לא נוסחה יפה במיוחד באופן כללי, אבל במקרה הפרטי שלנו היא דווקא תהיה פשוטה למדי.

עבור הפרמטריזציה של המעגל שבחרנו, \( x\left(t\right)=\cos t \) ו-\( y(t)=\sin t \) ולכן נקבל \( x^\prime(t)=-\sin t \) ו-\( y^{\prime}\left(t\right)=\cos t \), ולכן \( \sqrt{x^{\prime}\left(t\right)^{2}+y^{\prime}\left(t\right)^{2}}=1 \) - כמה נחמד זה כשהכל יוצא פשוט פתאום! אם כן, האינטגרל שלנו הוא \( \int_{0}^{2\pi}dt=2\pi \), וקיבלנו את האורך כמעט בלי מאמץ. כמובן, אתם עדיין צריכים להאמין הן לכך שהפרמטריזציה שלי מתארת נכונה את המעגל, והן שההגדרה שלי לאורך באמצעות נגזרות ואינטגרלים היא תקינה, אבל אני לא הולך לנסות ולשכנע אתכם יותר מכפי שכבר שכנעתי.

אגב, כדאי להעיר כאן שגם הגדרת הקירוב הפוליגונלי שלי, וגם ההגדרה עם הפרמטריזציה שתיהן מקרים פרטיים של המושג הכללי והחזק יותר של אינטגרל קווי - אינטגרל של פונקציה רב ממדית כלשהי שמחושב לאורך מסלול. המקרה שלנו מתקבל כשהפונקציה היא טריוויאלית.

לסיום, אני רוצה לחזור לרגע אל ההוכחה שבתחילת הפוסט. ההוכחה משחקת על התחושה האינטואיטיבית שלנו שככל שאנחנו מבצעים יותר שלבים בבניית העקומה-השואפת-לכאורה-למעגל שלנו, כך השינויים “נהיים קטנים יותר” במובן כלשהו. כדי להמחיש עד כמה התחושה הזו עשויה להיות מטעה, אני רוצה להציג מפלצת חביבה במיוחד, שראויה לפוסט שלם משל עצמה (ואף תקבל כזה מתישהו) - פתית השלג של קוך:

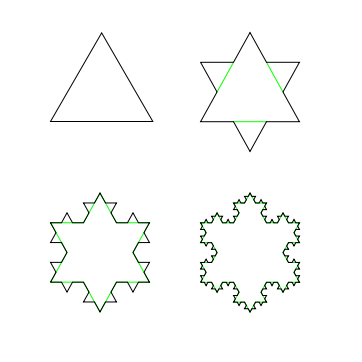
פתית השלג הוא פרקטל - הוא יצור שמורכב מעותקים מוקטנים של עצמו. איך בונים אותו פורמלית? ובכן, בונים סדרה של עקומות ששואפת אליו. מתחילים עם משולש שווה צלעות. לאחר מכן, לכל צלע של המשולש, בונים משולש שווה צלעות חדש על הצלע, כך שאחת מצלעותיו היא בדיוק השליש האמצעי של הצלע (ולכן גודל צלע המשולש החדש הוא שליש מגודל המשולש המקורי). את השליש הזה של האמצע מוחקים מהעקומה. כעת יש לנו צורה שנראית כמו מגן דוד שכזה. עכשיו מתחיל המשחק האמיתי: לכל אחד מששת הצ’ופצ’יקים של המגן דוד אנחנו מפעילים את אותה בניה כמו קודם. לכל צ’ופצ’יק שכזה יש שתי צלעות, ועל כל אחת מהן אנחנו בונים משולש שווה צלעות חדש. במילים אחרות, על כל צ’ופצ’יק אנחנו שמים שני צ’ופצ’יקים חדשים, קטנים יותר. ואז אנחנו עושים את זה שוב, ושוב, ושוב. הנה ציור של ארבעת השלבים הראשונים:

פתית השלג הוא הגבול של סדרת העקומות שנבנות באופן הזה. מה המובן הפורמלי של גבול כאן לא חשוב כרגע - אבל חשבו על כך שכל נקודה במרחב “יודעת” אחרי מספר סופי של צעדים בבנייה האם היא תהיה שייכת לפתית השלג הסופי או לא (אפשר להראות שלכל נקודה במרחב, קיים \( n \) כך שלכל עקומה בסדרה החל מהמקום ה-\( n \) והלאה או שהנקודה נמצאת על כל העקומות הללו, או שהיא לא נמצאת על אף אחת מהן).

וכעת הפאנץ’: למרות שנראה שהשינויים בפתית השלג “הולכים ונחלשים”, והצורה הסופית נראית סופית בהחלט, ההיקף שלה הוא אינסוף. זאת מכיוון שכל עקומה בסדרה ארוכה מקודמתה פי \( \frac{4}{3} \). מדוע? ובכן, בכל שלב בבנייה אנחנו לוקחים קו ישר (צד של צ’ופצ’יק), מחלקים אותו ל-3 חלקים, מעיפים אחד מהם ומוסיפים שני קווים חדשים מאותו אורך (הצ’ופצ’יק החדש). כלומר, מקו אחד קיבלנו 4 קווים חדשים, שהאורך שלהם הוא \( \frac{1}{3} \) מהאורך של הקו המקורי. לכן ההיקף גדל פי \( \frac{4}{3} \). זה אומר שההיקף של הצורה ה-\( n \)-ית בסדרה הוא גדול פי \( \left(\frac{4}{3}\right)^{n} \) מההיקף של המשולש המקורי, ולכן אין מנוס - ההיקף שואף לאינסוף, ולכן זה יהיה אורכו של פתית השלג (כאן דווקא כן ניתן להוכיח שהיקף פתית השלג שווה לגבול של סדרת אורכי העקומות ששואפות אליו).

מה אנחנו לומדים מזה? ובכן, דבר אחד בעיקר - כשאתם רואים בניות “אינסופיות” כאלו, אל תניחו ששום דבר מובן מאליו, ואל תסתמכו על האינטואיציה שלכם בלבד. אחרת באמת תקבלו ש-\( \pi=4 \).