הסריקה של גרהאם

אני לוקח הפסקה קצרה מהאלגברה הלינארית כי השאלה לדוגמה של תחרות התכנות של האוניברסיטה העברית (פרסומת זולה, כל עוד זה רלוונטי, מופיעה כאן) עשתה לי חשק לדבר קצת על בעיה גאומטרית ופתרונה - הבעיה של חישוב קמור של קבוצת נקודות במישור. זו בעיה ששייכת לתחום במדעי המחשב של גאומטריה חישובית - נתונה בעיה גאומטרית ואנו מחפשים פתרון אלגוריתמי עבורה, רצוי כזה שהוא יעיל ככל האפשר. בעיות כאלו צצות בכמה מהתחומים הפרקטיים ביותר במדעי המחשב - למשל, גרפיקה, ראייה ממוחשבת וכדומה - ולכן המהירות והיעילות הן קריטיות בבעיות שכאלו. הבעיה שלנו היא זו: יש קבוצה סופית של נקודות במישור, כלומר הקלט שלנו הוא סדרה של זוגות מהצורה \( \left(x,y\right) \) כאשר \( x,y \) הם מספרים ממשיים כלשהם, והמטרה שלנו היא למצוא מהו הקמור שלהן. לפני שנמצא מהו הקמור כדאי שנבין מהו קמור.

ובכן, קמור (בחולם), באנגלית Convex Hull, הוא מצולע - כלומר, צורה סגורה שמורכבת מסדרה של קווים שמתחברים כל אחד לבא אחריו בקודקודים, כמו משולש, מרובע וכדומה - שהוא גם קמור וגם מכיל את כל נקודות הקבוצה והוא גם המצולע הקמור הקטן ביותר שמכיל אותן. גם זה אולי לא ברור כי לא ברור מהי צורה קמורה - זוהי צורה שבה עבור כל זוג נקודות שנמצאות בתוך הצורה, גם הקו הישר המחבר אותן נמצא כולו בתוך הצורה; דוגמה לצורה שאינה קמורה היא פרסה, כי קו שנעביר בין שתי נקודות הנמצאות בקצוות השונים של הפרסה יעבור מחוץ לפרסה.

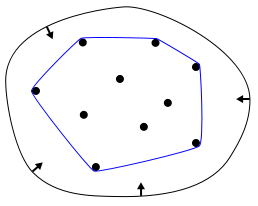
דרך חביבה אחת לחשוב על הקמור היא זו: נניח שיש לנו גומיה. אנחנו מותחים אותה בכוח עד שהיא מקיפה את כל הנקודות בקבוצה, ואז משחררים - הגומיה תתכווץ מייד על נקודות הקבוצה, ולאחר שזה ייגמר מה שנקבל הוא את הקמור. הנה תמונה שמראה זאת:

עוד דרך נחמדה לחשוב על הקמור היא זו: אם \( a,b \) הן שתי נקודות, אז אפשר לתאר את הקטע הישר שעובר ביניהן בתור הצירוף הלינארי \( \lambda_{1}a+\lambda_{2}b \) תחת התנאי ש-\( \lambda_{1}+\lambda_{2}=1 \) ו-\( \lambda_{1},\lambda_{2}\ge0 \). כלומר, הקטע הוא בדיוק קבוצת כל הנקודות מהצורה \( \lambda_{1}a+\lambda_{2}b \) (עבור ערכים גדולים או קטנים יותר של המקדמים נקבל משהו שהוא עדיין על הקו הישר שמחבר את הנקודות, אבל לא בקטע שבין שתיהן). למי שקשה לו לראות את זה, חשבו על זה כך: כאשר \( \lambda_{1}=1 \) אז \( \lambda_{2}=0 \) ולכן אנחנו בדיוק ב-\( a \); כאשר \( \lambda_{1}=0 \) אז \( \lambda_{2}=1 \) ולכן אנחנו בדיוק ב-\( b \); ולכן בין שני הקצוות הללו אנחנו באמצע הדרך בין \( a \) ו-\( b \). כמובן שאם זה עדיין לא משכנע אתכם הדבר הכי בטוח לעשותו הוא פשוט לחשב את משוואת הישר שעובר ב-\( a \) ו-\( b \) ולראות מה קורה.

כעת אפשר להכליל את הרעיון הזה. אם \( a_{1},a_{2},\dots,a_{n} \) היא קבוצה של נקודות אז צירוף קמור שלה הוא צירוף לינארי מהצורה \( \sum\lambda_{i}a_{i} \) כך ש-\( \sum\lambda_{i}=1 \) ו-\( \lambda_{i}\ge0 \) לכל \( i \). אפשר לחשוב על זה כעל נקודה שמתקבלת מאיזה ממוצע משוקלל של כל הנקודות בקבוצה. הקמור של קבוצות הנקודות הוא בדיוק אוסף כל הצירופים הקמורים שלהן (אם כי מה שמחפשים הוא את השפה של הקמור, שהיא המצולע-גומייה שדיברתי עליו קודם).

טוב, אז נניח שהבנו מה זה קמור. יש עכשיו שתי שאלות - איך מייצגים כזה דבר במחשב, ואיך מחשבים אותו. “איך מייצגים” זה קל - דרך אחת לייצג מצולעים (שהיא בהחלט לא הדרך היחידה) היא באמצעות סדרת הקודקודים שלהם, וזה מה שנחפש. אנלוגיית הגומייה נותנת את האינטואיציה הנכונה שקבוצת הקודקודים הזו היא תמיד תת-קבוצה של קבוצת הנקודות שמחשבים לה קמור, אבל אנחנו עדיין צריכים למצוא מהן הנקודות הללו ומה הסדר שבו הן מופיעות על הקמור. כאן נכנס לתמונה האלגוריתם של גרהאם, על שם המתמטיקאי רונלד גרהם (שפרט לפרסום כמתמטיקאי פורה ביותר בקומבינטוריקה, אחד ממחברי Concrete Mathematics וחבר טוב של ארדש גם ידוע בזכות כישורי הג’גלינג שלו).

האלגוריתם מתחיל מנקודה כלשהי שאנחנו יודעים בודאות שצריכה להיות על הקמור - למשל, זו בעלת קואורדינטת ה-\( x \) המינימלית (אם יש כמה נקודות עם קואורדינטת \( x \) מינימלית, בוחרים את זו מתוכן בעלת קואורדינטת ה-\( y \) המקסימלית). עכשיו ממיינים את כל הנקודות בהתאם לזווית ביחס לציר \( x \) שהם יוצרים עם הנקודה הזו - ככל שהזווית יותר גדולה, הנקודה באה מוקדם יותר. חשבו על זה כך - נניח שאנחנו מחברים לנקודה הזו זרוע אנכית שמצביעה כלפי מעלה, ואז מפילים אותה לכיוון הנקודות; המיון הוא לפי זמני ההגעה של הזרוע אל הנקודות.

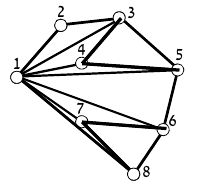
כעת, דרך ציורית לתאר את האלגוריתם היא זו: בכל פעם שבה הזרוע נתקלת בנקודה, היא “נשברת” - הבסיס שלה נותר תקוע על הנקודה, ואילו הזרוע מהנקודה והלאה ממשיכה בסיבוב שלה. זה נותן אינטואיציה לפיה האלגוריתם הוא פשוט “הנקודות על הקמור הן בדיוק הנקודות של הקבוצה, ממויינות על פי סדר הפגיעה של הזרוע בהן”, אבל ברור שיש כאן בעיה - לא תמיד כל הנקודות בקבוצה הן על הקמור; לרוב יש כאלו שנמצאות בתוך הקמור ולא אמורים להתחשב בהן. אז מה משתבש? גם כאן, כדאי לראות תמונה:

הבעיה מתחילה עם נקודה 4. במיון של הנקודות היא באה לפני נקודה 5, אבל ברור שהיא לא צריכה להיות על הקמור והזרוע הנשברת שלי לא אמורה להגיע אליה בכלל אי פעם. אז איך אפשר לפסול אותה? כאן נמצא הרעיון המרכזי של גרהאם - שימו לב שהקו שמחבר את נקודה 4 אל נקודה 5 מהווה פנייה שמאלה ביחס לקו שמחבר את נקודה 3 עם נקודה 4. גרהאם אומר - כל עוד אנחנו פונים ימינה ביחס לקו הקודם, הכל בסדר; אם פנינו שמאלה, זה אומר שהנקודה שבה התחילה הפניה שמאלה הזו היא מיותרת ואפשר לוותר עליה ולהוציא אותה מהקמור. בואו ננסה להבין למה זה נכון: נניח שאם אנחנו הולכים מנקודה 1 (לא זו שבציור) אל נקודה 2, וממנה פונים אל נקודה 3, נשאלת השאלה - מה היה קורה אם היינו הולכים מ-1 ישירות אל 3 ופוסחים על 2? האם נקודה 2 הייתה מצד ימין או מצד שמאל שלנו?

על פי השאלה הזו קם ונופל הכל, כי כשאנחנו בונים את הקמור בשיטה של גרהאם, הקמור הוא תמיד האיזור שנמצא מצד ימין שלנו. זה מה שנובע מכך שהמיון שלנו בוצע בעזרת זרוע שנעה עם כיוון השעון, כלומר צד שמאל שלה הוא האיזור שבו היא כבר הייתה וצד ימין הוא האיזור שבו היא עומדת להיות (מיון הפוך היה גורר היפוך של הכיוונים באלגוריתם - במקרה הזה דווקא פנייה ימינה הייתה גורמת להוצאת נקודה מהקמור). לכן, אם כשאנחנו הולכים מנקודה 1 לנקודה 3 נקודה 2 נמצאת בצד ימין של הקו, אין צורך להכניס אותה לקמור; ואם היא נמצאת בצד שמאל של הקו, הכרחי להכניס אותה לקמור. כעת, אם נקודה 2 נמצאת מימין לקו, אז אם הגענו אל 2 ואנחנו רוצים לעבור אל 3, אנחנו חייבים לפנות שמאלה, כי כרגע אנחנו מימין לקו; ואם נקודה 2 נמצאת משמאל לקו אז כדי להגיע ממנה ל-3 צריך לפנות ימינה. זה כל הסיפור. מי שזה עדיין לא ברור לו, מומלץ שיצייר בעצמו את הנקודות ויראה מה קורה.

מכאן ואילך האלגוריתם כבר די ברור: ראשית מכניסים לקמור את הנקודה שממנה מתחילים ואת הנקודה הראשונה במיון; וכעת בכל צעד של האלגוריתם מכניסים לקמור את הנקודה הבאה במיון, ואז בודקים אם כדי להגיע אל הנקודה הזו מהנקודה האחרונה כרגע בקמור מבצעים פניה שמאלה או ימינה. אם שמאלה, מעיפים מהקמור את הנקודה שהייתה האחרונה בו עד כה, ואחרת משאירים אותה. סוף הסיפור. לאלגוריתם הזה זמן ריצה מצויין - מציאת נקודת הקצה שבתחילת האלגוריתם מתבצעת בזמן \( O\left(n\right) \) בצורה הכי נאיבית, ושלב הסריקה עצמו גם הוא \( O\left(n\right) \) כי מטפלים בכל נקודה פעם אחת והטיפול הזה כולל רק בדיקה של תכונה שמערבת שלוש נקודות; צוואר הבקבוק של האלגוריתם הוא הצורך למיין, שמקפיץ אותנו לסיבוכיות \( O\left(n\log n\right) \). אם הנקודות כבר ממויינות בצורה כלשהי אפשר להשתמש בוריאציה על השיטה של גרהאם כדי לנצל את זה ולהימנע מהצורך למיין שוב (כך למשל אם הנקודות ממויינות לפי קואורדינטת ה-\( x \) האלגוריתם עובד כמעט באותה צורה, אבל צריך לשנות כמה דברים).

כמו שקורה לרוב בגאומטריה חישובית, זה דבר אחד לתאר את האלגוריתם, ודבר אחר לגמרי לממש אותו. אני מאוד מציע לאלו מכם שיודעים לתכנת לנסות ולעשות זאת כדי להרגיש את הבעיות הטכניות שצצות ואת השאלות שהרשיתי לעצמי להתעלם מהן כאן. למשל, איך מחשבים את הזוויות שעל פיהן ממיינים? (רמז: בכלל לא צריך לחשב זווית). ולמשל, איך יודעים אם פניה היא שמאלה או ימינה? אלו שאלות מעניינות לכשעצמן, ואם אכתוב עוד פוסטים על גאומטריה חישובית בוודאי אתייחס אליהן.