בעיית המעגל של גאוס (וגם קצת על טרחנות)

הפנו אותי לאתר הבא, שבו מציג כותב ישראלי משהו בשם “Q-space theory” שהיא “An attempt to intuitively unify physics”. ובכן, אתם ודאי יכולים לנחש מה אני חושב כשאני רואה משהו כזה. רוב תוכנו של האתר הוא קישורים לסרטוני יוטיוב שכבר הוסרו, אבל הסיבה שבגללה קישרו אותי אליו היא קובץ שבו מדובר על “התכנסות לערכו של פאי דרך הפתרונות הפיתגוראיים הטבעיים”. ובכן, אתם ודאי יכולים לנחש מה אני חושב כשאני רואה משהו כזה. אבל, כמו תמיד בעניינים הללו, לא הייתי טורח לכתוב על זה אם לא הייתה מתמטיקה מעניינת בפנים.

אם לסכם את המטרה של הקובץ, אחרי שמוצג בו מה שמוצג, הכותב כותב ש”הכפפה למתמטיקאי או למתמטיקאית היא: נסו לנסח את הממצא הנ”ל בשפה ובסטנדרטים הנדרשים על מנת לפרסם את הממצא באקדמיה”. ומהו אותו ממצא? ובכן, הכותב מתחיל עם הגדרה: הוא אומר ש-“\( i \) הוא “פתרון פיתגוראי טבעי” של \( a \) ו-\( b \) אם סכום ריבועים של \( a \) ו-\( b \) שווה ל-\( i \)”. בעולם המתמטי הרגיל קוראים ל-\( i \) כזה בדרך כלל “סכום ריבועים”. סכומי ריבועים, שלא יהיה לכם ספק, הם תחום מרתק ביותר בתורת המספרים שלעת עתה לא דיברתי עליו מספיק אם כי כבר דיברתי עליו קצת.

כעת, הכותב אומר שהוא “צפה את הקשר הבא מתוך שיקולים פיסיקליים”, וברשותכם אביא את הניסוח המקורי שלו:

בהינתן מספר טיבעי כלשהו \( n \), היחס בין מספר הפתרונות הפיתגוראיים הטבעיים שבהם סכום ריבועי הניצבים קטן או שווה ל-\( n \) (עם חשיבות לסדר הניצבים) לבין מחצית ערכו של \( n \) מתכנס לערך פאי חלקי 2 ככל ש-\( n \) גדל.

בנוסף, הוא מצרף קוד של תוכנית מחשב קצרה שמראה את ההתכנסות הזו. ברשותכם אמנע מלהציג אותו כאן, אבל הקוד בהחלט עובד והתוצאה שהוא מתאר בהחלט נכונה, וזה בהחלט נחמד שהוא גילה אותה באופן עצמאי. אז מה הבעיה כאן? שמדובר על ניסוח מחדש של בעיה בת 250 שנה לערך ושנפתרה כבר בידי גאוס - “בעיית המעגל של גאוס”. אמנם, צריך להיזהר קצת כי למרות שהאבחנה שיש פה התכנסות לפאי היא דבר אלמנטרי שנובע ממה שגאוס הראה, הבעיה האמיתית היא קצת יותר מורכבת ואין לה פתרון מלא עד היום.

אז מה הולך כאן ואיך מעגל נכנס לתמונה? ובכן, תשכחו מ”פתרון פיתגוראי טבעי” ותחשבו באופן גיאומטרי. אם \( a^{2}+b^{2}\le n \) (“הפתרונות הפיתגוראיים הטבעיים שבהם סכום ריבועי הניצבים קטן או שווה ל-\( n \)”) זה אומר שהנקודה \( \left(a,b\right) \) במישור \( \mathbb{R}^{2} \) היא במרחק לכל היותר \( \sqrt{n} \) מראשית הצירים, כלומר היא נמצאת בתוך העיגול שרדיוסו \( \sqrt{n} \). מכיוון שלא נוח לערב שורשים, בואו נדבר על עיגול ברדיוס \( n \) ולכן המשוואה היא \( a^{2}+b^{2}\le n^2 \). בנוסף, מכיוון שהוא מדבר רק על מספרים טבעיים הוא מדבר רק על הרבע הימני-עליון של העיגול - בואו נדבר על העיגול כולו, כלומר נרשה ל-\( a,b \) להיות גם שליליים (אבל עדיין מספרים שלמים). אז השאלה היא כזו: בתוך עיגול שרדיוסו \( n \), כמה נקודות יש שהקואורדינטות שלהן הן מספרים שלמים?

אפשר להגדיר את זה הכי פורמלית בעולם כך: \( N\left(n\right)=\left|\mathbb{Z}^{2}\cap\left\{ \left(a,b\right)\in\mathbb{R}^{2}|a^{2}+b^{2}\le n^{2}\right\} \right| \). בסימונים הללו, ההשערה שהועלתה היא שמתקיים \( \lim_{n\to\infty}\frac{N\left(n\right)}{n^{2}}=\pi \). את זה אפשר גם לסמן בצורה קצת שונה, שמתאימה קצת יותר לאופי של בעיות מסוג זה בתורת המספרים: \( N\left(n\right)=\pi n^{2}+o\left(n^{2}\right) \), או במילים: \( N\left(n\right) \) שווה ל-\( \pi n^{2} \) ועוד שגיאה שגדלה בקצב אסימפטוטי נמוך ממש יותר מ-\( n^{2} \), ובמילים אחרות אם מחלקים אותה ב-\( n^{2} \) ומשאיפים את \( n \) לאינסוף מקבלים אפס.

זו תוצאה יפה למדי; היא מראה, באופן אינטואיטיבי, שמספר הנקודות השלמות בתוך עיגול ברדיוס \( n \) הוא קירוב טוב לשטח של אותו עיגול. למה זה לא מפתיע ואפילו צפוי? ובכן, בגלל שאפשר לקרב את שטח עיגול היחידה באופן הבא: נגזור מעיגול היחידה ריבועים בעלי אורך צלע 1. כל ריבוע כזה הוא בעל שטח 1, ולכן שטח עיגול היחידה הוא מספר הריבועים שאנחנו יכולים לגזור ממנו “ועוד קצת” ממה שהולך בשוליים. הריבועים שנגזור יהיו בדיוק הריבועים שמוכלים בעיגול היחידה וגם קואורדינטות הקודקודים שלהם שלמות (למשל הריבוע עם הקודקודים \( \left(0,0\right),\left(0,1\right),\left(1,0\right),\left(1,1\right) \)) ואפשר למשל לזהות כל ריבוע עם הקואורדינטה הימנית-עליונה ביותר שלו (הריבוע שבדוגמה יזוהה עם \( \left(1,1\right) \)). בצורה הזו רוב הנקודות השלמות שבתוך העיגול יגדירו ריבוע שכולו בתוך העיגול למעט כמה מהנקודות שהן על השפה, אבל ככל ש-\( n \) גדול יותר כך מספר הנקודות הבעייתיות הופך לקטן יותר ביחס למספר הנקודות הכולל בעיגול (אינטואיטיבית: בגלל שהנקודות הבעייתיות הן באיזור השפה החד-ממדית, והנקודות ה”בסדר” הן באיזור הפנים הדו-ממדי) ולכן הקירוב ישתפר. זו אינטואיציה גסה מאוד אבל לטעמי היא מאפשרת להבין היטב מה הולך כאן.

מה גאוס הוכיח? ובכן, נסמן \( N\left(n\right)=\pi^{2}n+E\left(n\right) \) כש-\( E\left(n\right) \) היא פונקציית ה”שגיאה”; גאוס הוכיחש-\( \left|E\left(n\right)\right|\le2\sqrt{2}\pi n \) (לפחות על פי ויקיפדיה; ברפרנס שהם מביאים בכלל לא מדובר על הקבוע), ומכאן קל לראות ש-\( E\left(n\right)=o\left(n^{2}\right) \) וזה נותן את התוצאה שדובר עליה מייד. זה לא מסיים את הסיפור כי החסם של גאוס הוא עדיין גס למדי ויש חסמים טובים יותר; ההשערה היא ש-\( E\left(n\right)=O\left(n^{\frac{1}{2}+\varepsilon}\right) \), כלומר חזקה של \( n \) שהיא הרבה פחות מ-1 כמו בחסם של גאוס, אבל כיום החזקה הטובה ביותר שהגיעו אליה (על פי ויקיפדיה) היא \( 0.6298\dots \). בקיצור, חסם טוב על גודל השגיאה הוא עדיין אתגר פתוח במתמטיקה.

אני ארצה להוכיח כאן את התוצאה של גאוס, אבל לפני כן, עוד מילה אחת על “הכפפה למתמטיקאי”: כבר אמרתי כאן בעבר כי אחד מהמאפיינים של הטרחנים המתמטיים הוא הנטייה להמציא מחדש את הגלגל, לתת לו שם מפוצץ וכנראה לחשוב שאף אחד לא חשב על זה לפניך. כאן יש לנו מקרה קלאסי של הבעיה הזו - נותנים את השם המפוצץ “פתרונות פיתגוראיים טבעיים” למשהו שלא ממש זקוק לשם נוסף, מנסחים מחדש אבחנה שהיא כבר עתיקה למדי (בניסוח מילולי מסורבל) ומציגים את זה בתור “אתגר” לקהילה המתמטית. זה לא רציני. הדבר הראשון שצריך לעשות מישהו שמגלה תוצאה זו או אחרת במתמטיקה הוא לבדוק האם כבר שמעו עליה לפני שהוא מתחיל לפמפם אותה בתור תגלית שלו בתוספת אתגר למתמטיקאים שיואילו נא לנסח פורמלית ולהוכיח אותה. איכשהו אנשים סבורים לפעמים שניתן לעסוק במתמטיקה בלי ללמוד מתמטיקה כלל; אבל אפילו רמנוג’אן קרא ספרי מתמטיקה - ורובנו, מה לעשות, לא רמנוג’אן. מישהו שמצד אחד מתיימר לפתור את הבעיה המרכזית של עולם הפיזיקה כיום (תיאוריה מאוחדת) אבל מצד שני מראה שהוא לא מסוגל לעשות סקר ספרות אלמנטרי של בעיות מתמטיות פשוט לא יכול להילקח ברצינות.

הנה דרך נחמדה לבצע סקר ספרות שכזה. נניח שכבר הבנתם שמה שמעניין פה הוא העיגול כולו ולא רבע העיגול. אז אחד מהדברים שאפשר לעשות הוא לספור ממש כמה נקודות יש בו. הנה קוד בשפה Sage (שמבוססת על פייתון - ויסלח לי אלוהי הפייתון, אבל הבלוג מסרב להציג כאן רווח/טאב בתחילת שורה) שעושה את זה:

def N(n): return len([(a,b) for a in range(-n,n+1) for b in range(-n,n+1) if a^2+b^2<=n^2]) print [N(n) for n in range(10)]

שימו לב כמה העסק פשוט כאשר עובדים בשפה המתאימה - נדרשת בערך שורה אחת (שהיא אפילו קריאה, עבור מי שמכיר את השפה) כדי לעשות את החישוב שב”כפפה” דרש הרבה יותר קוד. כעת, אם מריצים את הקוד הזה יתקבל הפלט \( [1,5,13,29,49,81,113,149,197,253] \), ומה שעושים עם דבר כזה הוא ללכת לאנציקלופדיה האלקטרונית של סדרות מספרים. הסדרה מופיעה שם, כמו גם קישור לבעיית המעגל של גאוס. זו כמובן לא הדרך היחידה שאפשר לנקוט בה, אבל אני חושב שראוי להציג אותה כי לפעמים אנשים מפספסים את העובדה שסדרה של מספרים קונקרטיים שהיא לכאורה לא מעניינת לכשעצמה (כי מה אכפת לנו אם זה 197 שם ולא 196?) יכולה להיות מאוד מועילה כשמגששים באפלה של בעיה מסויימת (כמו גם שפת תכנות נוחה עבור מי שרוצה לחשב דברים “ביד”, אם כי צריך להיזהר ולא להגזים עם זה כי אינטואיציות באות לפעמים דווקא כשעושים את החישובים באמת ביד).

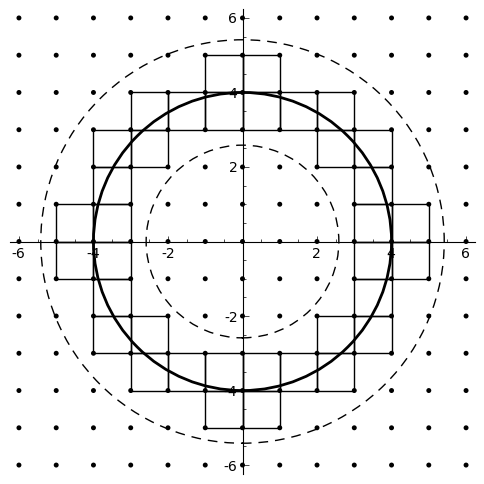
בואו נעבור להוכחת הטענה של גאוס (עם קבוע קצת יותר גדול ממה שנטען בויקיפדיה) באופן פורמלי יותר, אבל עדיין לא פורמלי עד הסוף כי אשתמש בשיקולים גיאומטריים שיהיו רבע נפנוף ידיים. ראשית, תמונה אחת שווה כאן אלף מילים:

העיגול שלנו מסומן בקו האחיד. הרעיון הוא זה שאמרתי קודם - יש התאמה בין ריבועי היחידה שקודקודיהם הם בעלי קואורדינטות שהן מספר שלם, והנקודות עם קואורדינטות שלמות במישור - לכל ריבוע פשוט מתאימים את הקודקוד הימני-עליון שלו. כעת, כל ריבוע שמוכל כולו בתוך העיגול, בפרט גם הקודקוד הימני-עליון שלו נמצא בתוך העיגול, ולכן התרומה של הריבוע לשטח (1) נספרת בהתאמה עם זה שהקודקוד של הריבוע נספר. אז מתי משהו יכול להשתבש? ברור שלא בריבועים שכולם מחוץ לעיגול - גם הקודקוד הימני-עליון שלהם מחוץ לעיגול ולכן איננו נספר. בעיה יכולה להתקיים באחד משני מקרים: או ריבוע שחלקו בתוך העיגול אבל הקודקוד הימני-עליון שלו בחוץ, ואז הוא תורם חלקית לשטח העיגול אבל לא לספירת הנקודות שבעיגול; או ריבוע שחלקו בתוך העיגול כולל הקודקוד הימני-עליון, אבל לא כולו בתוך העיגול ואז הוא לא תרם מספיק לשטח העיגול כדי לכסות על זה שהוא תרם נקודה לספירה.

מה שנעשה יהיה לבחור בגישה הכי נאיבית לחסימה של השגיאה כאן: על כל ריבוע שחלקו בתוך העיגול וחלקו מחוץ לעיגול, נגיד שגודל הטעות שהריבוע גרם לה הוא המקסימלי - 1. כל מה שעלינו להראות הוא שלא יכולות להיות הרבה טעויות, כלומר אנחנו רוצים לספור את הריבועים הבעייתיים. אלו בדיוק הריבועים שמצויירים באיור.

כעת, ריבוע שאורך צלעו יחידה הוא בעל אלכסון שאורכו \( \sqrt{2} \) (משפט פיתגורס). זה אומר שהמרחק המקסימלי בין כל שתי נקודות בריבוע הוא \( \sqrt{2} \). כעת, בואו ניקח ריבוע שחלקו בתוך העיגול אבל יש בו נקודה מחוץ לעיגול, ונמתח קו ישר ממרכז העיגול אל הנקודה בתוך הריבוע שהיא המרוחקת ביותר ממרכז העיגול. מרגע שהקו הזה מגיע אל הגבול של העיגול ועד שהוא מגיע אל הקודקוד הבעייתי הוא יכול לעבור רק מרחק של \( \sqrt{2} \) לכל היותר (כאן צריך קצת יותר הצדקה ואני מחפף), ולכן אם נצייר עיגול שרדיוסו גדול ב-\( \sqrt{2} \) מרדיוס העיגול המקורי שלנו, הוא יכיל את כל הריבועים הבעייתיים. העיגול הגדול יותר הזה הוא הגדול מבין שני העיגולים המקווקווים.

באופן דומה, הבה וניקח ריבוע שחלקו בתוך העיגול אבל לא כולו, אז אפילו הנקודה בו שמרחקה ממרכז העיגול הוא הקטן ביותר לא יכולה להיות במרחק גדול מ-\( \sqrt{2} \) משפת העיגול, אחרת כל הריבוע היה בפנים. לכן אפשר לצייר עיגול פנימי שרדיוסו קטן ב-\( \sqrt{2} \) מרדיוס העיגול - זה העיגול המקווקו השני. אם מסתכלים על השטח של העיגול המקווקו החיצוני, שממנו מחסירים את השטח של העיגול המקווקו הפנימי, מקבלים טבעת. כל הריבועים הבעייתיים נמצאים בשלמותם בתוך הטבעת הזו, ולכן שטח כל הריבועים הבעייתיים קטן או שווה לשטח הטבעת. רק ששטח טבעת קל לחשב - פשוט מחסרים משטח העיגול המקווקו החיצוני את שטח העיגול המקווקו הפנימי, ומקבלים:

\( \pi\left(n+\sqrt{2}\right)^{2}-\pi\left(n-\sqrt{2}\right)^{2}=4\pi\sqrt{2}n \)

וזהו ההפרש המקסימלי בין שטח העיגול (\( \pi n^{2} \)) ובין מספר הנקודות השלמות שבו (\( N\left(n\right) \)), מה שמסיים את ההוכחה וסוגר את עניין ה”כפפה”.