איך אלגברה לינארית מתקשרת לשרשראות מרקוב (ואיך כל זה קשור לגוגל)

שרשראות מרקוב

סדרת הפוסטים על אלגברה לינארית הגיעה במזל טוב לנקודה שבה אפשר לעצור ולעשות סיכומי ביניים לפני שצוללים בחומר הכבד הבא (מכפלות פנימיות), ולכן אני רוצה לנצל את ההזדמנות ולהציג נושא שהזכרתי בחטף קודם ולא דורש ידע באלגברה לינארית שטרם הוצג - שרשראות מרקוב. זה נושא ששייך לתורת ההסתברות ולכן הצגה פורמלית עד הסוף שלו תדרוש ממני לגלוש למונחים בהסתברות שעשויים לחסל קוראים שבסך הכל רוצים לראות שימוש מגניב באלגברה לינארית, ולכן אמנע עד כמה שאפשר מהם. מכיוון שאני עושה רק דברים פשוטים, איכשהו אצא מזה בשלום. או שלא.

שרשרת מרקוב היא מערכת מתמטית שמתארת התפתחות אקראית של תהליך לאורך זמן, בתנאי שלאותו תהליך יש תכונה של “חוסר זכרון” - העתיד של התהליך נקבע (אקראית) רק על פי ההווה, בלי תלות בעבר. ברקע תמיד יש קבוצה (סופית או בת-מניה) של “מצבים” אפשריים שבהם התהליך יכול להימצא בכל רגע נתון, והמצב הבא שאליו התהליך יגיע תלוי אך ורק במצב הנוכחי שלו ולא באופן שבו הוא הגיע למצב זה.

הנה דוגמה פשוטה: נניח שאתם מטילים קוביה שוב ושוב ושוב ולאחר כל הטלה רושמים את הסכום של כל ההטלות עד כה. התהליך הזה הוא שרשרת מרקוב; המצבים מתוארים על ידי הסכום הנוכחי שלכם, כלומר יש מצב לכל מספר טבעי. אם כרגע הסכום שלכם הוא 42, הרי שההסתברות שמכאן תגיעו אל 45 היא \( \frac{1}{6} \) (ההסתברות שיצא לכם בדיוק “3” בהטלת הקוביה), וזה בכלל לא משנה אם הגעתם ל-42 על ידי 7 הטלות רצופות של “6” או על ידי 42 הטלות רצופות של “1” או כל סדרה אחרת של מספרים. מרגע שהגעתם ל-42, ולא משנה איך, המשך התהליך יתנהג (הסתברותית) באותו אופן בדיוק.

ההגדרה נראית פשוטה, אבל היא למעשה חמקמקה למדי כי אפשר למדל באמצעות שרשרת חסרת זכרון גם תהליכים שנראים כאילו הם בעלי זכרון ועוד איך. הנה דוגמה: נניח שאנחנו משנים את חוקי משחק הקוביה שלנו כך שבפעם השניה שבה מוטל “1” הסכום שלנו מתאפס, ולא משנה כמה זמן עבר מאז ההטלה הראשונה של 1 (ואחר כך שוב פעם - אם יוצא 1 ממשיכים כרגיל, אבל אם יוצא 1 לאחר מכן, מאפסים את הסכום וחוזר חלילה). לכאורה יש כאן זכרון ועוד איך; אלא שאפשר למדל את המצבים שלנו בתור זוגות מהצורה \( \left(n,a\right) \) כאשר \( n \) הוא מספר טבעי כלשהו - הניקוד שלנו - ו-\( a \) הוא 0 או 1 - משתנה ש”זוכר” אם כבר יצא 1 מאז האיפוס האחרון או לא. די ברור שבהינתן \( \left(n,a\right) \), המשך התהליך לא תלוי באופן שבו הגענו למצב \( \left(n,a\right) \), אלא רק במצב זה עצמו. הלקח הוא שעל ידי מידול חכם, אפשר לתאר עם שרשרת מרקוב המון, המון דברים.

יש כמה סוגים שונים של שרשראות מרקוב, כשההבדל המרכזי בתיאוריה הוא בין שרשרת בזמן בדיד - שבה ה”זמן” מתואר על ידי מספרים טבעיים (“הצעד הראשון, הצעד השני, הצעד השלישי…”) לעומת שרשרת בזמן רציף, שבה הזמן הוא מספר ממשי. התיאוריה של המקרה הרציף מורכבת קצת יותר (אם כי דומה לזו של זמן בדיד) ואני לא הולך לדבר עליה בכלל. כמו כן, צריך להבדיל בין שרשראות שמרחב המצבים שלהן סופי, ואלו שמרחב המצבים שלהן אינו סופי (כמו השרשרת של המשחק שהצגתי זה עתה). דוגמה קלאסית לשרשרת עם מרחב מצבים סופי היא משחק “סולמות ונחשים” - המשבצות הן המצבים, ומעבר נקבע בהטלת קוביה (ועל פי הסולמות והנחשים, כמובן).

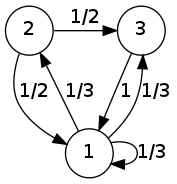
אני הולך לדבר רק על שרשראות שמרחב המצבים שלהן סופי, כי שרשראות כאלו ניתנות לתיאור באמצעות מטריצות. זאת מכיוון שאפשר לחשוב על כל שרשרת מרקוב בזמן בדיד בתור הילוך בגרף מכוון, כאשר הצמתים של הגרף הם המצבים של השרשרת, ועל הקשתות יש משקלים שמתאימים להסתברות המעבר בין צומת אחד לשני. לצורך פשטות, מסמנים את המצבים במספרים מ-1 ועד \( n \), ואז אפשר לתאר את השרשרת בעזרת מטריצה \( P \) מסדר \( n\times n \) כך ש-\( P_{ij} \) היא ההסתברות לעבור מהמצב \( i \) למצב \( j \). הנה דוגמה לאיך שזה נראה:

המטריצה המתאימה כאן היא \( P=\left(\begin{array}{ccc}\frac{1}{3} & \frac{1}{3} & \frac{1}{3}\\\frac{1}{2} & 0 & \frac{1}{2}\\1 & 0 & 0\end{array}\right) \). שימו לב לכך שבמטריצה הזו סכום כל שורה הוא 1. זה לא במקרה; השורה ה-\( i \) מייצגת את ההסתברויות לעבור מ-\( i \) לכל אחד מהמצבים האחרים (או להישאר במקום, מה שממודל בתור מעבר ל-\( i \)). מכיוון שאחד מאלו חייב לקרות, סכום כל ההסתברויות הוא בדיוק 1. למטריצה כזו, ששורותיה מסתכמות כולן ל-1, קוראים מטריצה סטוכסטית, ועוד נראה חשיבות לתכונה הזו בהמשך.

בפוסט שדיבר על כפל מטריצות הזכרתי את העובדה שאם \( A \) היא מטריצה מייצגת של גרף - כלומר, אם \( A_{ij} \) שווה ל-1 כשיש קשת מ-\( i \) אל \( j \) ו-0 אם אין כזו, אז \( A_{ij}^{k} \) הוא מספר המסלולים מאורך \( k \) מ-\( i \) אל \( j \) בגרף. מאותו נימוק ואותה הוכחה (שלא אכנס לפרטיה כאן אבל היא תרגיל מצויין לספקנים) אפשר לראות ש-\( P_{ij}^{k} \) היא בדיוק ההסתברות לעבור מהמצב \( i \) למצב \( j \) אחרי \( k \) צעדים; כלומר, אם התחלנו את השרשרת שלנו כאשר אנחנו במצב \( i \), וביצענו \( k \) צעדים, אז ההסתברות שבסוף ההרפתקאה הזו נהיה ב-\( j \) היא בדיוק, אבל בדיוק \( P_{ij}^{k} \). אני מאוד מקווה שהתוצאה הזו נראית לכם טריוויאלית לחלוטין; עכשיו עצרו לרגע וחשבו שאנחנו חיים בעולם ללא מטריצות וללא כפל מטריצות, וחשבו כיצד בעולם כזה היה נראה התיאור של החישוב של הסתברות המעבר מ-\( i \) אל \( j \) ב-\( k \) צעדים. זו דוגמה נאה לכך שבמתמטיקה ההגדרה הנכונה חשובה לעתים לא פחות מאשר המשפט הנכון - ברגע שרואים משהו מזווית הראייה הנכונה, הכל פתאום פשוט וכל החתיכות נופלות למקום. בדרך כלל אותה זווית ראייה היא משהו שכדי לשלוט בו נדרש קצת מאמץ (לאף אחד מאיתנו כפל מטריצות לא בא בקלות…) ולכן ההפשטה שיש כאן כל כך מועילה - מרגע שהבנו כפל מטריצות, אנחנו מסוגלים באמצעותו להבין המוני בעיות שונות ומשונות שאת כולן ניתן לתרגם לכפל מטריצות, ובכך לחסוך את המאמץ שהיה נדרש מאיתנו להבין כל אחת לחוד.

בואו נניח שאנחנו רוצים לשאול שאלה קצת יותר כללית: “אחרי \( k \) צעדים בשרשרת המרקוב, מה התפלגות המצבים שבהם נהיה?”. למה הכוונה בכך? התשובה הצפויה היא משהו בסגנון “בהסתברות חצי נהיה במצב מס’ 1, בהסתברות שליש במצב 2, ובהסתברות שישית במצב 3”. את זה אפשר לתאר על ידי וקטור עם \( n \) כניסות, \( v \), כך ש-\( v_{i} \) הוא ההסתברות להיות במצב \( i \). וקטור כזה יכול לתאר גם את המצב ההתחלתי של השרשרת - אף אחד לא אמר שחייבים להתחיל ממצב אחד ספציפי; אפשר לבחור את המצב שבו מתחילים גם כן באופן מקרי. לכן \( v=\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right) \) הוא וקטור שמתאר בחירה של כל מצב בהסתברות אחידה, ו-\( v=\left(0,1,0\right) \) הוא וקטור שמתאר התחלה ודאית במצב 2.

מה שצפוי כעת הוא שיתקיים שאם \( v \) הוא ההתפלגות הנוכחית שלנו בנקודת זמן כלשהי, אז \( Pv \) תהיה ההתפלגות אחרי צעד אחד. רק שזה לא עובד. כדי לראות זאת, בואו נניח ש-\( v=\left(1,0,0\right) \) - התחלה ודאית ממצב 1. נכפול ב-\( P \) שלמעלה, ונקבל \( Pv=\left(1,\frac{1}{2},1\right) \), שהוא בוודאי לא וקטור שמייצג הסתברות ולא כלום (יש כאן גם עניין לפיו \( v \) הוצג כוקטור שורה ולא עמודה, אבל אני מניח שהפורמליזם הזה לא מפריע לכם). למעשה, אם תחשבו על זה לרגע, לא הייתה שום סיבה להניח שזה יעבוד; האפקט הרצוי מושג דווקא על ידי פעולת כפל מהצד השני, שהיא משהו שפחות ראינו עד היום אבל היא לגיטימית לגמרי לכשעצמה: \( vP=\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right) \) - לא במפתיע, השורה הראשונה ב-\( P \) - ולא קשה להוכיח שבאופן כללי כפל משמאל אכן מעביר את ההתפלגות \( v \) להתפלגות הצפויה אחרי צעד אחד. וכמובן, \( vP^{k} \) היא ההתפלגות שאליה מגיעים אחרי \( k \) צעדים אם התחלנו ב-\( v \).

ואיך אלגברה לינארית מתקשרת אליהן

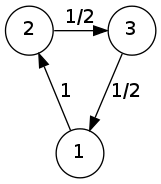
עכשיו בואו נעבור לאקשן. אגנוב דוגמה מהספר של Norris על שרשראות מרקוב פשוט כי היא כל כך מוצלחת. בואו נסתכל על השרשרת הפשוטה הבאה:

לצורך פשטות לא ציירתי את הקשתות מצומת לעצמו (אפשר להסיק מה הערכים שלהן). המטריצה של השרשרת הזו היא \( P=\left(\begin{array}{ccc}0 & 1 & 0\\0 & \frac{1}{2} & \frac{1}{2}\\\frac{1}{2} & 0 & \frac{1}{2}\end{array}\right) \). כעת נותנים לנו תרגיל - למצוא נוסחה כללית עבור ההסתברות לפיה אם נתחיל מהמצב \( 1 \), אז כעבור \( n \) צעדים גם כן נהיה במצב 1. בניסוח מטריציוני, שואלים אותנו מהי \( \left[P^{n}\right]_{11} \). זוהי שאלת אלגברה לינארית למהדרין, והדרך לפתרון שלה עוברת דרך ערכים עצמיים, אז בואו נתחיל מלמצוא את הערכים העצמיים לפי הספר. כאן יש לנו מזל - המטריצה קטנה, אז קל למצוא את הערכים העצמיים שלה, אבל לפעמים זה יכול להיות קשה למדי. הפולינום האופייני הוא

\( \left|\begin{array}{ccc}x & -1 & 0\\0 & x-\frac{1}{2} & -\frac{1}{2}\\-\frac{1}{2} & 0 & x-\frac{1}{2}\end{array}\right|=x\left|\begin{array}{cc}x-\frac{1}{2} & -\frac{1}{2}\\0 & x-\frac{1}{2}\end{array}\right|+\left|\begin{array}{cc}0 & -\frac{1}{2}\\-\frac{1}{2} & x-\frac{1}{2}\end{array}\right| \)

\( =x\left(x-\frac{1}{2}\right)^{2}-\frac{1}{4}=x^{3}-x^{2}+\frac{1}{4}x-\frac{1}{4}=x^{2}\left(x-1\right)+\frac{1}{4}\left(x-1\right)=\left(x-1\right)\left(x^{2}+\frac{1}{4}\right) \)

אם כן, מייד רואים ש-\( 1 \) הוא ערך עצמי, אבל פרט אליו אין ערכים עצמיים ממשיים: שני האחרים הם השורשים של \( x^{2}+\frac{1}{4} \), כלומר \( \pm\frac{i}{2} \). הנה צצים לנו מספרים מרוכבים בבעיה ממשית למהדרין, אבל אין כאן שום בעיה.

כעת, שימו לב שכל הערכים העצמיים הם שונים זה מזה, מה שמפשט לנו מאוד את החיים - מכיוון שהפולינום האופייני מתפרק לגורמים לינאריים שונים \( \left(x-1\right)\left(x-\frac{i}{2}\right)\left(x+\frac{i}{2}\right) \) נובע מייד ש-\( P \) לכסינה, כלומר \( P=U^{-1}\left(\begin{array}{ccc}1 & 0 & 0\\0 & \frac{i}{2} & 0\\0 & 0 & -\frac{i}{2}\end{array}\right)U \) עבור איזו \( U \) הפיכה שלא מעניינת אותנו. מכאן נובע מייד ש-\( P^{n}=U^{-1}\left(\begin{array}{ccc}1 & 0 & 0\\0 & \left(\frac{i}{2}\right)^{n} & 0\\0 & 0 & \left(-\frac{i}{2}\right)^{n}\end{array}\right)U \).

כעת אפשר לחשב ישירות את \( \left[P^{n}\right]_{11} \) על ידי חישוב \( U \) וביצוע הכפל, אבל \( U \) עשויה להיות מכוערת למדי ולא ברור עד כמה זה יוביל אותנו לנוסחה כללית טובה. במקום זאת ננקוט בתעלול אחר: מכיוון ש-\( P^{n} \) מתקבלת על ידי כפל המטריצה האלכסונית מימין ב-\( U \) ומשמאל ב-\( U^{-1} \), הרי ש-\( \left[P^{n}\right]_{11} \) תהיה צירוף לינארי של הכניסות השונות מאפס של המטריצה האלכסונית (כי זה מה שכפל מטריצות עושה - צירופים לינאריים). לכן \( \left[P^{n}\right]_{11}=\alpha\cdot1+\beta\cdot\left(\frac{i}{2}\right)^{n}+\gamma\left(-\frac{i}{2}\right)^{n} \). כל שנותר לעשות הוא למצוא את המקדמים \( \alpha,\beta,\gamma \) המתאימים. את זה עושים על ידי חישוב קונקרטי של \( \left[P^{0}\right]_{11},\left[P^{1}\right]_{11},\left[P^{2}\right]_{11} \) והצבה בנוסחה (שאמורה לעבוד לכל \( n \)). קל לראות שהערכים המתאימים הם 1,0,0, כך שקיבלנו את המשוואות:

\( \alpha+\beta+\gamma=1 \)

\( \alpha+\left(\frac{i}{2}\right)\left(\beta-\gamma\right)=0 \)

\( \alpha-\frac{1}{4}\left(\beta+\gamma\right)=0 \)

הפתרון למערכת הזו הוא \( \alpha=\frac{1}{5},\beta=\frac{2}{5}+\frac{1}{5}i,\gamma=\frac{2}{5}-\frac{1}{5}i \). שימו לב בפרט ש-\( \gamma=\overline{\beta} \) (צמוד מרוכב) וזכרו ש-\( -i=\overline{i} \), כך שקיבלנו את הפתרון הכללי:

\( \left[P^{n}\right]_{11}=\frac{1}{5}+\left(\frac{1}{2}\right)^{n}\left[\beta i^{n}+\overline{\beta i^{n}}\right]=\frac{1}{5}+\left(\frac{1}{2}\right)^{n}\left(2\mbox{Re}\left(\beta i^{n}\right)\right) \)

ב-\( i^{n} \) הכי קל לטפל בהצגה קוטבית שלא מצריכה חלוקה למקרים: \( i^{n}=e^{i\frac{\pi}{2}n} \), ולכן \( \beta i^{n}=\frac{2}{5}e^{i\frac{\pi}{2}n}+\frac{1}{5}ie^{i\frac{\pi}{2}n} \), ואם זוכרים ש-\( e^{i\theta}=\cos\theta+i\sin\theta \) מקבלים חיש קל ש-\( 2\mbox{Re}\left(\beta i^{n}\right)=\frac{4}{5}\cos\frac{n\pi}{2}-\frac{2}{5}\sin\frac{n\pi}{2} \), ולכן הפתרון לשאלה הוא:

\( \left[P^{n}\right]_{11}=\frac{1}{5}+\left(\frac{1}{2}\right)^{n}\left(\frac{4}{5}\cos\frac{n\pi}{2}-\frac{2}{5}\sin\frac{n\pi}{2}\right) \)

השתמשתי כאן בתעלול או שניים כדי לפשט את הפתרון, אבל לא יותר מדי - זו גם שיטת העבודה הכללית. בהערת אגב, אפשר היה לפשט עוד את הפתרון על ידי ביצוע משהו שאולי היה נראה לחלקכם כמו רמאות: כשקיבלתי את נוסחת הנסיגה \( \alpha\cdot1+\beta\cdot\left(\frac{i}{2}\right)^{n}+\gamma\left(-\frac{i}{2}\right)^{n} \) להגיד “בגלל שאנחנו יודעים שהפתרון הוא ממשי, אז אפשר להחליף את הנוסחה הזו בנוסחת הנסיגה \( \alpha+\left(\frac{1}{2}\right)^{n}\left(\beta\cos\frac{n\pi}{2}+\gamma\sin\frac{n\pi}{2}\right) \)”, אבל כמו שאנחנו רואים זה לא משפיע על התוצאה.

טוב, אז מה ראינו כאן? גם אם לא נכנסתם לעובי הפרטים הטכניים, לב העניין כאן היה שהתנהגות המערכת לטווח ארוך - ההסתברות לעבור ממצב \( i \) למצב \( j \) אחרי \( n \) צעדים עבור \( n \) כללי - ניתנה באמצעות צירוף לינארי של חזקות של הערכים העצמיים של המטריצה שמתארת את המערכת. זו המחשה נאה ביותר לאופן שבו הערכים העצמיים של המערכת מתארים אותה, והם בעצם אבן היסוד שמרגע שמגלים אותה, שאר התנהגות המערכת נובעת מאליה. למי שתוהה למה ערכים עצמיים הם מושג כה חשוב ומרכזי - זו התחלה.

בדוגמה שלמעלה היה לנו מזל - המטריצה הייתה לכסינה. באופן כללי זה לא כך, ואז התנהגות המערכת שנובעת מהערכים העצמיים מסובכת יותר אבל עדיין ניתנת לתיאור שיטתי באמצעות צורת ז'ורדן של מטריצות, שאני מקווה להציג מתישהו. נעזוב את זה לבינתיים.

בואו ננסה עכשיו להבין קצת יותר טוב מה הנוסחה ל-\( \left[P^{n}\right]_{11} \) אומרת: שאחרי \( n \) צעדים, אם התחלנו מהמצב 1, ההסתברות שלנו להיות ב-1 היא חמישית ועוד איזה “גורם כאוטי” שמתואר באמצעות \( \frac{4}{5}\cos\frac{n\pi}{2}-\frac{2}{5}\sin\frac{n\pi}{2} \) (הסינוסים והקוסינוסים מעידים על כך שהגורם הזה הוא מחזורי, דבר לא מפתיע בפני עצמו) אבל כזה שההשפעה שלו דועכת אקספוננציאלית עם הזמן, מה שבא לידי ביטוי בכפל ב-\( \left(\frac{1}{2}\right)^{n} \). פורמלית, בבירור \( \lim_{n\to\infty}\left[P^{n}\right]_{11}=\frac{1}{5} \), מה שאומר שאנחנו מצפים, אם ניתן למערכת לרוץ זמן ארוך אחרי שהתחילה ממצב 1, להגיע לכך שבכל פרק זמן ההסתברות שהמערכת תהיה במצב 1 היא \( \frac{1}{5} \), ולכן שבריצה לטווח ארוך המערכת תהיה במצב 1 חמישית מהזמן. עכשיו אני רוצה לדבר על האופן שבו מבצעים ניתוח של “התנהגות לטווח ארוך” שכזו.

לב העניין הוא במה שמכונה “התפלגות אינוריאנטית” (או “שיווי משקל”, או אולי “התפלגות סטציונרית”). בואו נתחיל מלשים לב לכך שהעובדה ש-1 היה ערך עצמי של \( P \) בדוגמה למעלה לא הייתה מקרית. באופן כללי, אם כל השורות של מטריצה מסתכמות לאותו מספר \( a \) (או כל העמודות מסתכמות לאותו מספר \( a \)) אז \( a \) הוא ערך עצמי של המטריצה. דרך אחת לראות זאת היא כך: אם כל השורות של המטריצה \( A \) מסתכמות ל-\( a \) אז \( v=\left(1,1,\dots,1\right) \) הוא וקטור עצמי של המטריצה כי \( Av=\left(a,a,\dots,a\right)=av \) (כי כפל ב-\( v \) פשוט סוכם את כל השורות של \( A \) אחת אחת). אם כל העמודות של \( A \) מסתכמות ל-\( a \) אז מתקיים \( vA=\left(a,a,\dots,a\right) \) אבל לא הגדרנו ערכים עצמיים באמצעות פעולת הכפל משמאל. מצד שני, זה לא משנה כי מתקיים ש-\( vA=\left(Av\right)^{t}=A^{t}v \), כאשר \( t \) מציין את אופרטור השחלוף: \( \left[A_{ij}^{t}\right]=A_{ji} \) (שיקוף הכניסות של \( A \) ביחס לאלכסון הראשי). לא קשה להוכיח של-\( A \) ול-\( A^{t} \) אותו פולינום אופייני (הפיתוח של הדטרמיננטה יהיה זהה פרט לכך שכאשר מפתחים אחת מהן על פי שורה, את השניה מפתחים על פי עמודה) ולכן אותם ערכים עצמיים.

במקרה שלנו שורות \( P \) מסתכמות ל-1, ולכן תמיד יתקיים ש-\( P\cdot\left(1,\dots,1\right)=\left(1,\dots,1\right) \) ולכן 1 הוא ערך עצמי של \( P \). מה שזה אומר הוא שקיים וקטור \( v \) שמקיים \( vP=v \) גם בכפל משמאל; הוקטור הזה כלל לא צריך להיות דומה ל-\( \left(1,\dots,1\right) \). בואו נגלה אותו עבור \( P \) של הדוגמה שלנו; אנחנו רוצים לפתור את מערכת המשוואות \( \left(\begin{array}{ccc}-1 & 0 & \frac{1}{2}\\1 & -\frac{1}{2} & 0\\0 & \frac{1}{2} & -\frac{1}{2}\end{array}\right)v=0 \) (שחלפתי את \( P \) והפחתתי 1 מהאלכסון הראשי). קצת דירוג מטריצות ונקבל \( \left(\begin{array}{ccc}1 & 0 & -\frac{1}{2}\\0 & 1 & -1\\0 & 0 & 0\end{array}\right)v=0 \), כלומר הצורה הכללית של הפתרון \( v \) היא \( v=\left(\frac{1}{2}\alpha,\alpha,\alpha\right) \) עבור פרמטר \( \alpha \) כלשהו.

מבין כל הוקטורים העצמיים \( v \) האפשריים, יש אחד שמעניין אותנו במיוחד: כזה שמייצג התפלגות מצבים. כדי שוקטור יקיים את התכונה הזו, הוא צריך להיות אי שלילי (כלומר, שכל כניסה בו תהיה גדוהל או שווה מ-0, כי אין אצלנו משמעות להסתברות שלילית), והוא צריך שהכניסות שלו יסתכמו ל-1 (בפועל אפשר לקחת כל וקטור אי שלילי ופשוט לחלק את כל הכניסות שלו בסכום הכניסות). במקרה שלנו מתקבל וקטור התפלגות שכזה עבור \( \alpha=\frac{2}{5} \): נקבל \( u=\left(\frac{1}{5},\frac{2}{5},\frac{2}{5}\right) \). ה-\( \frac{1}{5} \) בכניסה הראשונה היא לא מקרית, כפי שאסביר בקרוב.

בואו נבין מה מצאנו כרגע: מצאנו וקטור התפלגויות \( u \) כך ש-\( uP=u \). כלומר, זוהי התפלגות מצבים שאם השרשרת שלנו הגיעה אליה, היא תישאר בה לעד. כמובן, בכל צעד בשרשרת אנחנו עדיין עוברים ממצב למצב באופן הסתברותי, אבל ההתפלגות הכוללת של כל המצבים שבהם אנו עשויים להיות נותרת ללא שינוי. זה מסביר את התארים של “התפלגות אינוריאנטית/סטציונרית” ו”שיווי משקל”.

התוצאה המעניינת הראשונה על התפלגויות אינוריאנטיות מסבירה את ה-\( \frac{1}{5} \) שקיבלנו ב-\( u \). אם יש לנו שרשרת מרקוב סופית (הסופיות קריטית פה) כך שעבור מצב \( i \) כלשהו מתקיים ש-\( \lim_{n\to\infty}\left[P_{ij}^{n}\right]=\pi_{j} \) לכל מצב \( j \) (אנו דורשים רק שהגבול יהיה קיים; \( \pi_{j} \) הוא איך אנחנו מסמנים אותו אם הוא קיים) אז הוקטור \( \left(\pi_{1},\pi_{2},\dots,\pi_{k}\right) \) הוא וקטור התפלגות אינוריאנטית. במקרה של \( P \) שלנו אכן מתקיים \( \lim_{n\to\infty}\left[P_{12}^{n}\right]=\lim_{n\to\infty}\left[P_{13}^{n}\right]=\frac{2}{5} \) אבל לא טרחתי לחשב את הנוסחה שלהם כדי לראות זאת.

אם כן, ההתפלגות האינוריאנטית מתארת את ההתנהגות לטווח ארוך של \( P \) אם קיימת כזו - \( P \) “שואפת” להתפלגות האינוריאנטית. השאלה המהותית יותר היא מתי התכנסות כזו אכן מובטחת. בואו נראה דוגמה פשוטה ביותר שבה אין התכנסות - שרשרת שבה יש שני מצבים, כך שמכל אחד עוברים לשני בהסתברות אחת. לשרשרת הזו יש את המטריצה \( P=\left(\begin{array}{cc}0 & 1\\1 & 0\end{array}\right) \). בבירור 1 הוא ערך עצמי של \( P \). מרחב הוקטורים העצמיים השייכים לערך העצמי 1 נפרש על ידי \( \left(\alpha,\alpha\right) \) ולכן \( \left(\frac{1}{2},\frac{1}{2}\right) \) היא התפלגות אינוריאנטית (חשבו על זה קצת - זה פשוט למדי אחרי שמבינים מה הולך כאן). אלא ש-\( P \) לא מתכנסת לשום מקום; שימו לב ש-\( P^{2}=\left(\begin{array}{cc}1 & 0\\0 & 1\end{array}\right) \) ולכן \( P^{3}=P \), ובאופן כללי כל כניסה של \( P \) “מזגזגת” בין 0 ו-1 ולכן לא מתכנסת. הבעיה כאן היא בכך שהשרשרת שלנו היא מחזורית. אין צורך להסתבך עם הגדרות בעייתיות פה כדי לתאר מחזוריות של תהליך אקראי: די לנו להגדיר ששרשרת היא לא מחזורית אם \( \left[P^{n}\right]_{ii}>0 \) עבור \( n \) גדול דיו לכל \( i \) (אפשר לראות שהגדרה זו שקולה לדרישה שהמחלק המשותף הגדול ביותר של קבוצת ה-\( n \)-ים שעבורם \( \left[P^{n}\right]_{ii}>0 \) עבור \( i \) מסויים הוא 1).

אפשר היה אולי לחשוב שמספיק לדרוש שמצב אחד בלבד יהיה לא מחזורי, ואז אי-המחזוריות שלו “תפעפע” לשאר המחרוזת. זה גם נכון, בתנאי שלא ניתן לפרק את המחרוזת ל”רכיבי קשירות” שלא מתקשרים זה עם זה. מבלי להיכנס יותר מדי להגדרות הפורמליות, שרשרת מרקוב היא בלתי פריקה אם לכל מצב \( i \) ולכל מצב \( j \), אם התחלנו מ-\( i \) יש לנו סיכוי להגיע מתישהו ל-\( j \) (קצת יותר פורמלית, \( \left[P^{n}\right]_{ij}>0 \) עבור \( n \) גדול דיו). אפשר להראות ששרשרת מרקוב שיש בה מצב אחד בלבד שהוא אי מחזורי והיא אי פריקה תהיה אי מחזורית בכל המצבים שלה.

כעת אפשר לנסח את מה שהוא כנראה המשפט החשוב ביותר בכל הפוסט: אם נתונה לנו שרשרת מרקוב אי מחזוריות ובלתי פריקה (לא בהכרח סופית!) וקיימת לה התפלגות אינוריאנטית \( \pi=\left(\pi_{1},\dots,\pi_{k}\right) \), אז בלתי תלות בשאלה מה ההתפלגות שבה מתחילים את ריצת השרשרת, לכל מצב \( j \) ההסתברות שהשרשרת תהיה ב-\( j \) בצעד ה-\( n \) שואפת ל-\( \pi_{j} \) כאשר \( n \) שואף לאינסוף (\( \lim_{n\to\infty}\mbox{P}\left(X_{n}=j\right)=\pi_{j} \) כאשר \( X_{n} \) הוא המשתנה המקרי שמתאים ל”המצב של השרשרת בזמן \( n \)”). בפרט זה אומר ש-\( \lim_{n\to\infty}\left[P^{n}\right]_{ij}=\pi_{j} \) לכל \( i,j \). פירוש הדבר הוא שבשרשראות אי מחזוריות ובלתי פריקות, ההתפלגות האינוריאנטית של השרשרת מתארת בדיוק את ההתנהגות לטווח ארוך שלה. ההוכחה של המשפט היא מקסימה גם היא אבל אינה פשוטה ולא אציג אותה כעת.

ואיך כל זה קשור לגוגל

לסיום הפוסט אני רוצה להסביר איך כל זה קשור לגוגל. בשנת 1998 פרסמו סרגיי ברין ולארי פייג’, מייסדי גוגל, מאמר (שהיה תוצאה של פרוייקט שעשו באוניברסיטת סטנפורד) שהציע שיטת דירוג עמודי אינטרנט שנקראה PageRank (על שם לארי פייג’, לא בגלל ש-Page הוא דף). כמובן, גוגל הוא הרבה יותר מאשר רק השיטה הזו, ומנוע החיפוש האמיתי של גוגל משתמש באינספור הרחבות, וריאציות ותיקונים על השיטה הזו, אבל הרעיון הבסיסי בשיטה הוא חזק לכשעצמו ואציג רק אותו.

אנחנו רוצים לדרג דפים לפי ה”חשיבות” שלהם, אבל איך קובעים מתי דף הוא חשוב? ברין ופייג’ הציעו את ההגדרה המטופשת “דף חשוב הוא דף שהרבה דפים חשובים מקשרים אליו”. מטופשת, כי היא נראית מעגלית וחסרת טעם. אלא שהיא בכלל לא מטופשת.

פורמלית, אצל ברין ופייג’ ה-PageRank של דף הוא סכום על ה-PageRank של הדפים שמקשרים, כאשר לכל דף שמקשר אליו אותו PageRank מחולק במספר הדפים שאליהם אותו דף מקשר. בנוסף לכך יש איזה פרמטר \( d \) שתכף אסביר את חשיבותו. הנוסחה של ברין ופייג’ היא

\( \mbox{PR}\left(A\right)=\frac{1-d}{N}+d\sum_{T_{i}}\frac{\mbox{PR}\left(T_{i}\right)}{C\left(T_{i}\right)} \)

כאשר \( N \) הוא מספר הדפים הכולל באינטרנט (ליתר דיוק - באוסף הדפים שעבורם מחשבים את PageRank) הסכום רץ על כל הדפים \( T_{i} \) שמקשרים ל-\( A \), ו-\( C\left(T_{i}\right) \) הוא מספר הלינקים הכולל שיוצא מ-\( T_{i} \). הגדרה מעגלית, אבל בכלל לא בעייתית. הנקודה היא שזה בדיוק מה שמקבלים אם ממדלים גלישה באינטרנט בתור שרשרת מרקוב.

הרעיון הוא לחשוב על האינטרנט בתור גרף אחד גדול, שבו כל דף הוא צומת, ויש קשת מדף א’ לדף ב’ אם דף א’ מקשר אל דף ב’. כעת אנחנו חושבים על שרשרת מרקוב שבה המשתמש מטייל בגרף. בכל פעם שבה הוא בצומת מסויים, הוא בוחר את הצומת הבא לעבור אליו בהסתברות שווה מבין כל הצמתים שניתן להגיע אליהם מהצומת הנוכחי. כמו כן, בהסתברות \( 1-d \) (אצל ברין ופייג’ \( d \) נקבע ל-\( 0.85 \) בתחילה) המשתמש “ישתעמם” ופשוט יעבור לדף אחר באינטרנט (כולו!) באופן אקראי. אני משאיר לכם לחשוב איך אפשר לתאר את כל זה פורמלית בתור שרשרת מרקוב - זה לא קשה.

אין ספק שיש לנו כאן תיאור נאיבי ביותר של האופן שבו אנשים גולשים באינטרנט, אבל אפשר לשפר אותו אם יש בכך צורך (למשל, שלא כל הלינקים בתוך עמוד יקבלו משקל זהה), וגם בגרסתו הבסיסית התיאור הזה נותן תוצאות מועילות למדי. כעת, שימו לב ששרשרת המרקוב הזו היא אי מחזורית (כי תמיד יש סיכוי שתחזור לדף שהתחלת ממנו - אפילו אחרי צעד אחד אם אתה “משתעמם”) ואי פריקה (שוב, ה”שיעמום” מבטיח שתוכל להגיע לכל דף מכל דף אחר בהסתברות נמוכה כלשהי). לכן היא מתכנסת להתפלגות אינוריאנטית - ומה זו ההתפלגות האינוריאנטית הזו? ניחשתם נכון, קל לראות ש-\( \mbox{PR}\left(A\right) \) היא בדיוק התפלגות אינוריאנטית של השרשרת הזו. המעגליות של ההגדרה נפתרה: זו בדיוק אותה מעגליות שיש בהגדרה בסגנון “\( Av=v \)” - אם \( A \) נתונה, כמובן שזו לא הגדרה מעגלית של \( v \) כלל.

בקיצור, \( \mbox{PR}\left(A\right) \) מתאים בדיוק להתנהגות לטווח ארוך של גולש אקראי במודל הגלישה שהצענו. מבחינה אינטואיטיבית המודל הזה קורץ למדי. עם זאת, עוד לא הבהרנו שתי נקודות חשובות: ראשית, למה בכלל קיים וקטור עצמי של 1 שהוא אי-שלילי? כל עוד לא הוכחנו קיום של כזה, לא הוכחנו שיש בכלל פתרון למערכת המשוואות שמגדירה את \( \mbox{PR} \). שנית, איך מוצאים את הוקטור הזה בפועל? אנחנו מדברים כאן על מטריצות ענקיות (ברין ופייג’ דיברו במאמר על מטריצות מסדר 26 מיליון על 26 מיליון; בפועל כמובן שגוגל מתעסקים עם דברים גדולים יותר).

אלו שאלות טובות והתחום של מציאת ערכים עצמיים למטריצות גדולות הוא חשוב ומעניין ומסובך בפני עצמו ואיני יכול להיכנס אליו יותר מדי כרגע, אבל אני יכול לומר משהו בקיצור: המשפט שמהווה את עמוד השדרה לשיטה של ברין ופייג’ נקרא משפט פרון-פרובניוס והוא אחד מעמודי התווך של האלגברה הלינארית. לא אוכל להציג את המשפט בשלמותו (הוא אומר הרבה דברים), אבל אספר את מה שרלוונטי לנו כרגע.

בהינתן מטריצה \( A \) מעל \( \mathbb{R} \) או \( \mathbb{C} \), הרדיוס הספקטרלי שלה \( \rho\left(A\right) \) הוא הערך המוחלט המקסימלי של הערכים העצמיים של \( A \) - אם תרצו, חשבו על זה בתור רדיוס העיגול הקטן ביותר ב-\( \mathbb{C} \) שמרכזו בראשית הצירים ומכיל בתוכו את כל הערכים העצמיים של \( A \) (שהם בסופו של דבר איברים של \( \mathbb{C} \)). שימו לב כי \( \rho\left(A\right) \) הוא תמיד מספר ממשי. כעת, החלק הרלוונטי עבורנו ממשפט פרון-פרובניוס אומר כי אם \( A \) היא מטריצה חיובית (שכל כניסותיה הן מספרים ממשיים גדולים מאפס, כמו במקרה של \( P \) של ברין ופייג’) כך ש-\( r=\rho\left(A\right) \), אז \( r \) הוא ערך עצמי של \( A \) (זה בפני עצמו לא טריוויאלי; אם \( r=\rho\left(A\right) \) כל מה שאפשר לעשות באופן כללי הוא לומר שקיים ערך עצמי \( \lambda \) - שיכול להיות שלילי או מרוכב - כך ש-\( r=\left|\lambda\right| \)), וכל ערך עצמי אחר של \( A \) הוא קטן ממש בערכו המוחלט מ-\( r \), וקיים וקטור עצמי של \( r \) (הן מימין והן משמאל) שכל הכניסות שלו חיוביות.

כעת, מה הרדיוס הספקטרלי של מטריצה סטוכסטית כמו אלו שבהן התעסקנו בפוסט הזה? ברור שהוא לפחות 1 כי 1 הוא וקטור עצמי. ממשפט פרון-פרובניוס עולה כי אם 1 הוא לא הרדיוס הספקטרלי אז קיים \( \lambda>1 \) ממשי שגם הוא ערך עצמי, עם וקטור עצמי \( v \) שכל כניסותיו הן ממשיות חיוביות, כלומר \( Av=\lambda v \). קל מאוד לראות שזה בלתי אפשרי: נניח ש-\( v_{max} \) הוא ערכה של הכניסה הגדולה ביותר ב-\( v \), אז מכיוון שכל שורה של \( A \) מסתכמת ל-1, רואים מייד שכל כניסה ב-\( Av \) היא לכל היותר \( v_{max} \), אבל ב-\( \lambda v \) יש כניסה שהיא גדולה ממש מ-\( v_{max} \). לכן במקרה שלנו הרדיוס הספקטרלי הוא בדיוק 1, ולכן קיים למטריצה וקטור עצמי אי-שלילי עבור הערך העצמי 1, ולכן קיימת התפלגות אינוריאנטית, בדיוק כפי שרצינו (יש עוד דרכים להוכיח את עניין הרדיוס הספקטרלי בלי תותח כבד כמו פרון-פרובניוס, אבל לצרכים שלנו כאן זה הכי התאים).

אם כן, ראינו שהתורה של שרשראות מרקוב (עם מרחב מצבים סופי) קשורה בקשר בל-ינתק לאלגברה לינארית; ראינו איך ערכים עצמיים הם השחקן המרכזי בניתוחים שנובעים מכך; ראינו בחטף משפט מרכזי שעוסק בערכים עצמיים של מטריצות חיוביות - פרון-פרובניוס - ואת האופן שבו הוא, יחד עם התורה של שרשראות מרקוב, משמשים באפליקציות מציאותיות ביותר. זה היה רק קצה הקרחון של השימושים של הנושאים שהזכרתי בפוסט הזה, אבל לטעמי קצה הקרחון הזה לכעצמו מספיק כדי להטביע את הטיטאניק.