איך להערים על מיון ערימה

בפוסט הקודם, שאני מניח שקראתם ואם לא מומלץ שתעשו זאת לפני הפוסט הנוכחי, דיברתי על אלגוריתמי מיון בסיסיים. שלושת הבסיסיים - מיון בחירה, מיון הכנסה ומיון בועות - היו איטיים למדי; זמן ריצתם היה \( \Theta\left(n^{2}\right) \) כאשר \( n \) הוא אורך הרשימה שאותה רוצים למיין. מבין השלושה זה שמשיג את הביצועים הטובים ביותר הוא מיון הכנסה, שלא חייב לרוץ זמן של בערך \( n^{2} \) תמיד; זה תלוי עד כמה הרשימה שהוא פועל עליה כבר ממויינת (לעומת זאת, עבור מיון בחירה ומיון בועות בכלל הרבה פחות משנה איך הרשימה נראית - הם עדיין יבצעו המון פעולות בהכרח).

ראינו גם את מיון מיזוג, שכבר הציע שיפור משמעותי בזמן הריצה - \( \Theta\left(n\log n\right) \). ה”בעיה” במיון מיזוג הייתה שהוא לא ביצע מיון במקום, כלומר ללא שימוש בזכרון נוסף; במימוש שלנו של פעולת ה”מיזוג” השתמשנו ברשימת עזר שגודלה כגודל הרשימה שאותה מיזגנו. אמנם, אפשר להסתדר גם בלי זה, אבל במחיר מיזוג מסובך יותר ותובעני יותר מבחינת כמות הפעולות שהוא דורש. אני רוצה להציג עכשיו אלגוריתם מיון שמבצע את המיון במקום, וזמן הריצה שלו הוא \( \Theta\left(n\log n\right) \). למיון הזה קוראים מיון ערימה.

מיון ערימה הוא מעין הכללה של מיון בחירה ומיון בועות. בואו נתחיל מלהבין את הבעיות של המיונים הללו ואיך אפשר להתגבר עליהן. מיון בחירה, כזכור, היה אלגוריתם פשוט ביותר מבחינה רעיונית: “מצא את המקסימום ברשימה, העבר אותו לסוף הרשימה; עכשיו שכח מהאיבר האחרון ברשימה ופעל באותו האופן על תת-הרשימה שכוללת את כל האיברים פרט לאחרון, וכו’ וכו’”. הבזבזנות של האלגוריתם מתבטאת בכך שבכל איטרציה אנחנו מחפשים את המקסימום ברשימה, וקרוב לודאי שחוזרים על השוואות שכבר ביצענו בעבר. השאלה היא אם אין דרך כלשהי לחסוך את הזמן שמציאת המקסימום דורשת.

באופן כללי, התשובה היא “לא”. אם יש לנו רשימה מאורך \( n \), אז כדי למצוא את המקסימום בה אנחנו חייבים לעבור על כל \( n \) האיברים. אבל כאן מדובר על סיטואציה מורכבת יותר: מדובר על רשימה שאנחנו עומדים לקרוא שוב ושוב, כשבין כל שתי קריאות אנחנו מבצעים בה שינוי קטן - סילוק של איבר אחד מתוכה. האם ניתן לבצע עיבוד כלשהו לרשימה שיאפשר לפעולת “מציאת מקסימום” להתבצע במהירות גדולה יותר?

הרי לנו דוגמה קלאסית לבעיה שמצריכה מבנה נתונים. מבנה נתונים הוא דרך ייצוג כלשהי של מידע שמאפשרת לפעולות מסוימות להתבצע באופן יעיל. בדרך כלל עלינו ליצור את מבנה הנתונים בצורה כלשהי, אולי על בסיס נתונים קיימים, וזה דורש זמן כלשהו של עיבוד מקדים; אולם מרגע שמבנה הנתונים כבר קיים, התקווה היא שביצוע פעולות עליו ידרוש זמן קצר יחסית.

במקרה שלנו, מבנה הנתונים צריך לתמוך בשתי פעולות שאותן הוא יבצע במהירות: הוא צריך לאפשר מציאת מקסימום יעילה, והוא צריך לאפשר הוצאת מקסימום יעילה (דהיינו, הוצאה של איבר מתוך המבנה; אבל אנחנו מסתפקים במקרה הפרטי שבו האיבר הזה הוא במקרה גם המקסימום, ולכן אולי יהיה יותר פשוט להוציא אותו מאשר להוציא איבר כללי). יש מבנה נתונים פשוט מאוד שתומך בפעולות הללו - ערימה (ובאנגלית Heap; אין קשר ל-Heap שאליו מתייחסים בתכנות בתור מקום שזכרון מוקצה מתוכו).

מה שאנו עומדים לראות הוא שניתן לבנות ערימה מתוך רשימה של \( n \) איברים בזמן \( \Theta\left(n\right) \)(ליתר דיוק, אנחנו הופכים את הרשימה לערימה), ולאחר מכן ניתן לבצע פעולה של מציאת מקסימום בזמן \( \Theta\left(1\right) \) ושל הוצאת מקסימום בזמן \( \Theta\left(\log n\right) \). מכאן בבירור זמן הריצה של האלגוריתם יהיה \( \Theta\left(n\log n\right) \), שכן הוא יכלול קודם כל את בניית הערימה, ולאחר מכן \( n \) איטרציות שבכל אחת מהן נמצא ונוציא את המקסימום.

ובכן, איך נממש ערימה? ברור שאם יש לנו רשימה שהיא כבר ממויינת, אז היא יכולה לתפקד בתור ערימה מצוינת: כדי למצוא את המקסימום פשוט נחזיר את האיבר האחרון, וכדי להוציא את המקסימום פשוט נוציא את האיבר האחרון (ונסמן שאורך הרשימה קטן ב-1 אם יש בכך צורך). טוב ויפה, אבל אם הרשימה כבר ממויינת אז כל הדיון מיותר, וגם לא ברור איך אפשר (אם בכלל) לבנות מתוך רשימה כללית של \( n \) איברים רשימה ממויינת בזמן \( \Theta\left(n\right) \). אז כדאי להקל קצת את הדרישות.

הדרישה מרשימה ממויינת היא זו: האיבר הגדול ביותר הוא בסוף. לפניו נמצא האיבר השני בגודלו, ולפניו האיבר השלישי בגודלו וכן הלאה. ערימה מקלה את הדרישה הזו קצת. במקום לחשוב על הרשימה בתור “קו ישר” של איברים, אנחנו חושבים עליה בתור עץ בינארי. עץ בינארי נראה כמו עץ משפחה - יש לו “צמתים” שמייצגים איברים ברשימה, ולכל צומת יכולים להיות עד שני בנים (זה פירוש ה”בינארי” שבשם - עד שני בנים) , שהם בעצמם צמתים, כך שלכל צומת יש לכל היותר אב יחיד. אם אנחנו נמצאים בצומת כלשהו אנחנו יכולים “לטייל” אל אחד מהבנים שלו, ומשם אל אחד מהבנים של הבן, וכן הלאה; נקבל כך מסלול בתוך העץ. הדרישה מערימה היא שכל מסלול כזה יהיה ממוין לפי הגודל (מהגדול ביותר לקטן ביותר). לא קשה לראות שזה שקול לדרישה “כל צומת גדול מכל בניו”, שתיקרא תכונת הערימה.

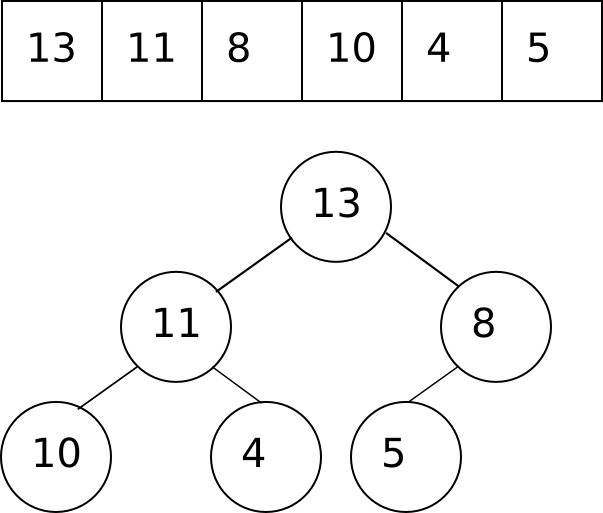
תמונה אחת שווה אלף מילים. הנה ערימה, הן בייצוג שלה בתור רשימה, והן בייצוג שלה בתור עץ בינארי:

 

כפי שאתם רואים, אין צורך לתחזק מבנה של עץ בתוך המחשב עצמו; אפשר להסתפק לצורך כך ברשימה, עם המוסכמה לפיה הבנים של התא מספר \( k \) הם בדיוק התאים מספר \( 2k+1 \) ו-\( 2k+2 \), ושהצומת בראש העץ (השורש של העץ) הוא תא מספר 0 (ולכן הבנים שלו הם תאים 1 ו-2; והבנים של תא 1 הם תאים 3 ו-4 בעוד שהבנים של תא 2 הם תאים 5 ו-6, וכן הלאה). כאן אנחנו קצת מגבילים את עצמנו בכך שאנחנו דורשים שהעץ יהיה בנוי מ”שכבות” שבהן יש את כל הצמתים האפשריים למעט בשכבה האחרונה, של הצמתים שאין להם בנים כלל (צמתים כאלו נקראים עלים) ובשכבה הזו נמצאים כל הצמתים עד למקום מסויים ושם הם מפסיקים. לעץ כזה קוראים “עץ בינארי כמעט מלא” (עץ מלא הוא עץ שבו כל השכבות מלאות). המבנה הפשוט הזה של העץ הוא שמאפשר לאחסן אותו כל כך בקלות בתוך רשימה; ייצוג עצים כלליים הוא מטלה קשה בהרבה.

טוב, אז מה זו ערימה - הבנו. איך היא מיוצגת על ידי רשימה - הבנו. מה הלאה?

מציאת האיבר המקסימלי בערימה היא טריוויאלית - זה חייב להיות האיבר שבשורש. שהרי אם המקסימום אינו בשורש, יש לו אבא; ומכיוון שהאבא חייב להיות גדול לפחות כמו הבן, והבן הוא המקסימלי, אז או שהגענו לסתירה (מה שיקרה בהכרח אם אין שני איברים ברשימה שהם מאותו הגודל), או שהאבא שווה בגודלו לבן ואז אפשר לחזור על אותו שיקול לגבי האבא, עד שנגיע לכך שגם השורש עצמו חייב להיות שווה לאיבר המקסימלי.

אם כן, למצוא את המקסימום זה קל. אבל איך אפשר, אחרי שהוצאנו את המקסימום מהערימה, “לתקן” אותה כך שהיא עדיין תהיה ערימה תקנית?

ראשית, מכיוון שערימה חייבת להיות עץ בינארי כמעט מלא, אנחנו לא יכולים סתם להעלים את הצומת של האבא; מה שנעשה יהיה להחליף אותו עם הבן הימני ביותר בשכבה התחתונה, ואז להקטין את הגודל של הערימה ב-1 (מה שגורם לנו “לא לראות יותר” את הצומת של המקסימום, בדיוק כמו שעושים במיון בחירה).

אחרי החלפה שכזו, העץ עשוי לאבד את תכונת הערימה, כי הצומת שבשורש עשוי להיות קטן מאחד מבניו. אז מה עושים? כמו במיון בועות, “מפעפעים” אותו למטה. משווים אותו לבנים שלו, ואם אחד מהם גדול ממנו, מחליפים ביניהם (אם שניהם גדולים ממנו אז מחליפים בינו לבין הגדול מביניהם), ואז חוזרים על הפעולה עבור תת-העץ שבו היה הבן קודם. באופן הזה מובטח לנו שכאשר התהליך הסתיים, העץ יקיים שוב את תכונת הערימה (ולכן בפרט השורש יכיל את המקסימום החדש). לפעולה הזו - ה”פעפוע” למטה של הצומת שמפר את תכונת הערימה - אקרא heapify (אל תהיו רעים אלי, זה מה ש-CLRS משתמשים בו).

הנה הקוד:

def heapify(list, n, heapsize)
  max = n
  l = 2*n+1 #left son
  r = 2*n+2 #right son
  max = r if r < heapsize and list[max] < list[r]
  max = l if l < heapsize and list[max] < list[l]
  return if max == n
  list.swap(max, n)
  heapify(list, max, heapsize)
end

הקוד די מסביר את עצמו (אני מקוה). רק שימו לב לבדיקות אם r < heapsize ו-l < heapsize שמטרתן למנוע מאיתנו לגלוש אל מעבר לקצה הערימה (מה שעשוי להיות מסוכן כי האיזור הזה לא בהכרח ריק או מכיל ג’יבריש; הוא יהיה עשוי להכיל איברים שכבר מיינו) ולקריאה הרקורסיבית בסוף של heapify.

היתרון האדיר שנותן לנו מעבר לחשיבה על הקלט בתור עץ במקום הישארות עם רשימה הוא שתהליך הפעפוע הזה לא יכול לקחת הרבה זמן; הוא בהכרח ידרוש לכל היותר \( \log n \) צעדים. למה? כי עומק של עץ בינארי כמעט מלא עם \( n \) צמתים הוא \( \log n \). אסביר זאת בפירוט בהמשך. לעת עתה, בואו נטפל בשאלה האחרונה שנותרה פתוחה: איך בכלל בונים ערימה מתוך רשימה לא מסודרת?

התשובה פשוטה. ראשית כל, אפשר לחשוב גם על רשימה מבולגנת בתור עץ בינארי כמעט מלא, פשוט כזה שלא מקיים בהכרח את תכונת הערימה. אז בואו פשוט נתחיל לתקן אותו. מה שכבר ראינו הוא ש-heapify מקבלת צומת n, ועושה הוקוס-פוקוס שמקיים את התנאי הבא: אם תת-העץ ששורשו n הוא ערימה תקנית פרט אולי לכך ש-n מפר את תכונת הערימה, אז אחרי הפעלת heapify תת-העץ כולו יקיים את תכונת הערימה.

אם כן, אם יש לנו כרגע עץ שהוא בלאגן אחד גדול, להפעיל את heapify על השורש שלו לא הולך ליצור לנו ערימה מתוך העץ (כי העץ עשוי להפר את תכונת הערימה במקומות רבים ולא רק בשורש). לכן נטפל בעץ “מלמטה למעלה”. אנחנו יודעים שתת-העץ של כל עלה הוא מן הסתם רשימה חוקית (כי הוא מכיל רק צומת בודד), אז בואו נעבור על כל הצמתים מהרמה הלפני-אחרונה והלאה, ולכל אחד מהם נריץ את heapify על תת-העץ שלו:

def make_heap(list)
  (list.length-1).downto(0) |n| heapify(list,n, list.length)
end

אני מציג כאן סגנון כתיבה סטנדרטי ברובי שהוא קצת חריג למי שלא מכיר את השפה. הנה דרך אחרת לכתוב את אותו הדבר בדיוק:

def make_heap(list)
  n = list.length
  while n > 0
    n = n - 1
    max_heapify(list,n, list.length)
  end
end

כלומר, תפקיד הסוגריים המסולסלות כאן הוא בסך הכל להכניס את הכל לאותה השורה, מה שאפקטיבי כאשר מריצים פקודות בנות שורה אחת.

שימו לב שהקוד שלי טיפה בזבזני כי אני עובר על כל הצמתים ברשימה, כולל העלים. אפשר היה להתחיל גם מהחצי.

מה זמן הריצה של make_heap? בבירור הוא \( O\left(n\log n\right) \): אני עובר על כל הצמתים ברשימה, כלומר \( n \), ולכל אחד אני מריץ את heapify שזמן הריצה שלו הוא \( O\left(\log n\right) \). עם זאת, ניתוח קצת יותר זהיר של מה שהולך כאן שאציג בהמשך מראה שזמן הריצה הוא בעצם \( \Theta\left(n\right) \). הסיבה לכך היא ש-heapify דורש פחות זמן ריצה כשהוא מורץ על צמתים נמוכים יותר, ואין כל כך הרבה צמתים גבוהים בעץ. נחזור לכך אחר כך.

כעת אפשר סוף סוף להציג את הקוד של מיון ערימה. כצפוי, אין הבדל מהותי בינו לבין הקוד של מיון בחירה:

def heapsort(list)
  make_heap(list)
  for n in 1..list.length
    list.swap(0,list.length - n)
    heapify(list, 0, list.length - n)
  end
  return list
end

בהתחלה יוצרים ערימה. בכל איטרציה מעבירים את האיבר שב-0 (המקסימלי) לסוף, מקטינים ב-1 את גודל הערימה, ומתקנים את מה שקלקלנו עם heapify. לטעמי זה אלגוריתם פשוט, אלגנטי ונחמד.

עכשיו בואו נעבור לניתוחים המתמטיים. ראשית כל אנחנו צריכים להבין עובדות בסיסיות על עצים בינאריים. נפתח בהגדרה: הגובה של עץ בינארי הוא אורך המסלול הארוך ביותר בו, כאשר “מסלול” הוא פשוט סדרה של צמתים כך שכל אחד מהם הוא אביו של זה שבא אחריו. אפשר למדוד אורך של מסלול או על ידי מספר הצמתים הכולל בו, או על ידי מספר הצעדים שאנו מבצעים בו, כלומר מספר הצמתים במסלול פחות 1 (ולכן מסלול שמכיל רק צומת אחד - כלומר, כזה שבו אנו “נשארים במקום”, הוא מאורך 0). אני מעדיף את ההגדרה השניה ולכן בה אשתמש.

כעת, עץ בינארי כמעט מלא שגובהו \( h \) מכיל בדיוק \( h+1 \) שכבות, שכולן מלאות למעט אולי האחרונה. כמה צמתים יש בכל שכבה?

בשכבה מס’ 0 יש רק צומת יחיד - השורש. בשכבה מס’ 1 יש שני צמתים - הבנים של השורש. בשכבה מס’ 2 יש 4 צמתים - הבנים של הבנים של השורש, וכן הלאה. בכל שכבה יש לכל היותר פי 2 צמתים מאשר בשכבה הקודמת, שכן לכל צומת בשכבה הקודמת יש לכל היותר 2 בנים. מכאן שקל מאוד לקבל חסם עליון על מספר הצמתים בעץ בינארי כמעט מלא מעומק \( h \):

\( 1+2+4+\dots+2^{h}=2^{h+1}-1 \)

השוויון הזה הוא פשוט הנוסחה הרגילה לטור הנדסי מתכנס (ומי שלא מאמין - שיכפול את אגף שמאל ב-\( \left(2-1\right) \) ויראה מה קורה).

מצד שני, אם העץ הוא מעומק \( h \), אז כל השכבות עד לשכבה ה-\( h \) ולא כולל חייבות להיות מלאות, ולכן יש בעץ לפחות \( 1+2+\dots+2^{h-1}=2^{h}-1 \) צמתים.

קיבלנו שמתקיים, עבור עץ בינארי כמעט מלא עם \( n \) צמתים, הקשר הבא: \( 2^{h}-1\le n\le2^{h+1}-1 \), כלומר \( \lg\left(2^{h}\right)\le\lg\left(n+1\right)\le\lg\left(2^{h+1}\right) \), כלומר \( h\le\lg\left(n+1\right)\le h+1 \). מכאן ש-\( h=\Theta\left(\log n\right) \). עכשיו רק נותר לשים לב לכך ש-heapify קורא לעצמו רקורסיבית לכל היותר \( h \) פעמים (כי בכל קריאה רקורסיבית הוא יורד רמה אחת בעץ) וקיבלנו שזמן הריצה של heapify הוא \( O\left(\log n\right) \) (זה לא \( \Theta \) כי הוא עשוי לעצור מייד, תלוי בנסיבות). מכאן נובע מייד שזמן הריצה של make_heap הוא \( O\left(n\log n\right) \) ושזמן הריצה של heapsort הוא גם כן \( O\left(n\log n\right) \). לכן ההוכחה האחרונה, שזמן הריצה של make_heap הוא \( O\left(n\right) \), עשויה להיראות טיפה מיותרת. היא לא, משתי סיבות: ראשית, כי משתמשים בערימות לעוד דברים חוץ מאשר מיון (למשל, תור עדיפויות). שנית, כי זו הוכחה מגניבה.

אז ההוכחה הולכת כך: זמן הריצה של make_heap הוא סכום זמני הריצה של heapify על כל הצמתים בגרף. זמן הריצה של heapify על צומת שגובהו \( t \) הוא \( O\left(t\right) \). אם כן, כמה צמתים יש בגרף שגובהם \( t \)?

יש צומת אחת בגובה \( h \) - השורש. שני צמתים בגובה \( h-1 \) (הבנים). ארבעה בגובה \( h-2 \) וכן הלאה. אם כן, באופן כללי, ישנם \( 2^{k} \) צמתים בגובה \( h-k \), וזאת עד \( k=h \) שבו יש לנו לכל היותר \( 2^{h} \) צמתים (נניח שיש בדיוק, זה רק מגדיל את זמן הריצה). קיבלנו שזמן הריצה הכולל של make_heap על עץ בינארי כמעט מלא מגובה \( h \), שנסמן \( T\left(h\right) \), הוא:

\( T\left(h\right)=\sum_{k=0}^{h}2^{k}\cdot O\left(h-k\right) \)

כלומר, אם לכתוב במפורש, קיים \( c \) כך ש-\( T\left(h\right)\le c\cdot\sum_{k=0}^{h}2^{k}\left(h-k\right) \), לכל \( h \) גדול דיו. זה מזמין החלפת משתנה: \( t=h-k \). נקבל:

\( T\left(h\right)\le c\cdot\sum_{t=0}^{h}2^{h-t}t=c\cdot2^{h}\cdot\sum_{t=0}^{h}\frac{t}{2^{t}}\le c\cdot2^{h}\cdot\sum_{t=0}^{\infty}\frac{t}{2^{t}} \)

למה עברתי ל-\( \sum_{t=0}^{\infty}\frac{t}{2^{t}} \) בסוף? כי זה טור מוכר מאוד, יחסית. הוא נראה כמעט כמו טור הנדסי, למעט זה שהוא גם מוכפל ב-\( t \). הנה הדרך הסטנדרטית לטפל בו, למי שצריך להתחיל מאפס ולא זוכר כלום על טורים מהצורה הזו, אבל כן בעל ידע בסיסי בחשבון אינפיניטסימלי (ברמה של טורי פונקציות): ראשית, נחשוב על הטור כעל פונקציה במשתנה \( x \) שנראית כך: \( f\left(x\right)=\sum_{t=0}^{\infty}t\cdot x^{t} \) (והטור מתקבל על ידי הצבת \( x=2^{-1} \)). זו דוגמה נאה לפונקציה שמוגדרת על ידי טור חזקות, מה שאומר שאפשר לעשות לה כל מני דברים נחמדים - למשל, אינטגרציה איבר-איבר. לרוע המזל, זה לא עובד כמו שצריך, כי \( \int x^{t}=\frac{x^{t+1}}{t+1} \) והיינו רוצים שיהיה \( t \) במכנה, אז מה שנעשה יהיה להוציא \( x \) משני האגפים: \( \frac{f\left(x\right)}{x}=\sum_{t=0}^{\infty}tx^{t-1} \). אינטגרציה לאגף שמאל נותנת לנו כעת \( \sum_{t=0}^{\infty}x^{t}=\frac{1}{1-x} \) (הנוסחה האחרונה היא הנוסחה לטור הנדסי; אם אתם לא מאמינים, כפלו את אגף שמאל ב-\( 1-x \) ותראו מה אתם מקבלים).

אם כן, קיבלנו ש-\( f\left(x\right)=x\cdot\left(\frac{1}{1-x}\right)^{\prime}=\frac{x}{\left(1-x\right)^{2}} \). סכום הטור, כזכור, הוא \( f\left(\frac{1}{2}\right) \) ולכן קיבלנו \( \sum_{t=0}^{\infty}\frac{t}{2^{t}}=\frac{1/2}{\left(1-1/2\right)^{2}}=\frac{1/2}{1/4}=2 \). המסקנה: \( T\left(h\right)\le2^{h}\cdot2=O\left(n\right) \), כנדרש.

אני אוהב את ההוכחה הזו משתי סיבות. ראשית, העובדה שניתוח קצת יותר זהיר מהניתוח הפשטני של make_heap נותן לנו חסם עדיף אסימפטוטית מעידה יפה, כבר בשלב מוקדם זה של דיונים על אלגוריתמים, עד כמה העניינים הללו עשויים להיות עדינים לפעמים. שנית, אנחנו רואים כאן היטב איך ידע בסיסי במתמטיקה הוא הכרחי כדי לטפל בצורה נכונה בניתוחי הסיבוכיות של אלגוריתמים שכאלו. בפוסט הבא, שבו נדבר על מיון מהיר, העניינים הללו יודגשו אף יותר.