הפנטגרמה והפיתגוראים

על מה אתם חושבים כשאתם רואים את הסמל הבא?

באופן מצער למדי, הסמל הזה - פנטגרמה - הפך בימינו למזוהה עם כת השטן והפך למעט מוקצה מחמת מיאוס (כמובן, הרבה פחות מאשר סמל אחר, ההוא שההודים משתמשים בו זה אלפי שנים). זה חבל הן מסיבות תרבותיות, שכן פנטגרמה מופיעה בשלל הקשרים תרבותיים אחרים שכלל אינם קשורים לכת השטן (ויש גם ניואנסים; אם קודקוד הפנטגרמה כלפי מטה זו כת השטן, ואם הוא מעלה זה פאגניזם וכיוצא בזה), אבל גם בגלל שמבחינה מתמטית מדובר על צורה גיאומטרית מגניבה ביותר, ובפוסט הזה אני רוצה להראות את אחת מהדרכים שבהן היא מגניבה - הוכחת קיום של מספרים אי רציונליים, כלומר כאלו שאינם ניתנים להצגה כיחס בין שני מספרים שלמים.

עוד בראשית ימי הבלוג הצגתי הוכחה לכך שהשורש של 2 אינו רציונלי, וזמן מה לאחר מכן גם הצגתי הוכחה כללית לכך ששורש של מספר שלם הוא או מספר שלם בעצמו או אי רציונלי. הוכחה כללית שכזו הייתה ידועה כבר למתמטיקאים היוונים הקדמונים ומופיעה אצל אוקלידס, ב-300 לפנה”ס, אבל הגילוי כנראה בוצע הרבה קודם, ונהוג לייחס אותו לפיתגורס, שחי בסביבות 600 לפנה”ס. האגדות אוהבות לספר שפיתגורס וחסידיו האמינו כי כל דבר ניתן לתיאור בידי מספרים רציונליים, והגילוי שיש דברים שלא ניתן לתאר כך זעזע אותם כל כך עד שהטביעו את היפסוס, הפיתגוראי שגילה זאת (גרסה אלטרנטיבית: הוא טבע כעונש מהאלים. גרסה אלטרנטיבית: הוא הוטבע/טבע כעונש על כך שחשף את דבר הגילוי לעולם החיצון, מה שהפר את קוד השתיקה הכללי של הפיתגוראים בלי קשר לאי רציונלית; גרסה אלטרנטיבית: הוא הוטבע בכלל בגלל ויכוח עם פיתגורס על דודקהדרון; גרסה אלטרנטיבית: הוא מת בשיבה טובה. היסטוריה של המתמטיקה זה עסק מסובך).

נשאלת השאלה, מה היפסוס בעצם גילה? מה המספר האי רציונלי שלו? לרוב חושבים שמדובר על שורש 2 ושההוכחה של היפסוס דומה להוכחה ה”סטנדרטית” שהצגתי בבלוג, אבל יש גם דעות אלטרנטיביות. אמנם, שורש 2 צץ מעצמו כשאנחנו מסתכלים על ריבוע עם אורך צלע 1 ומפעילים את משפט פיתגורס כדי לחשב את אורך האלכסון שלו, אבל אין סיבה להניח שמשפט פיתגורס היה חשוב באופן מיוחד לפיתגוראים; השם שלו הוא בסך הכל תוצר של נסיבות היסטוריות. לעומת זאת, הפנטגרמה הייתה סמל קדוש לפיתגוראים, ולכן הוכחה שמוצאת בה משהו אי רציונלי נראית יותר סבירה (אבל כמובן, את האמת אין לדעת - לא נותרו ממצאים כתובים של פיתגורס עצמו). ההוכחה הזו היא גם גיאומטרית יותר באופיה מההוכחה ששורש 2 אינו רציונלי, והתעלול המרכזי בה הוא יפהפה לחלוטין, כך שיש בה ערך גם אם אנחנו כבר מכירים את ההוכחה על שורש 2.

ראשית כל יש להבין כיצד פנטגרמה נוצרת. אנחנו מתחילים מצורה פשוטה יותר - מחומש משוכלל:

הרעיון במחומש משוכלל הוא שזהו מצולע בעל 5 צלעות שוות באורכן, שכל הזוויות בו שוות.

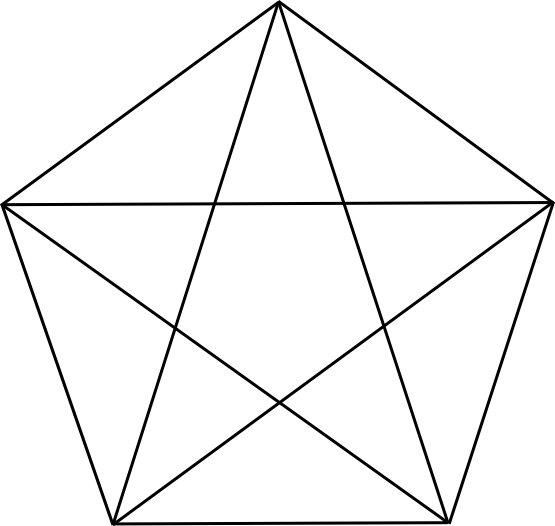
עכשיו, בהינתן מחומש אפשר לקבל ממנו פנטגרמה באופן הבא - פשוט מציירים את כל האלכסונים, כלומר את כל הקווים שמחברים קודקודים שאינם סמוכים:

בעצם, הציור שלעיל הוא מה שקורה כשלוקחים את חמשת הקודקודים של מחומש ומחברים כל קודקוד לכל הקודקודים האחרים האפשריים. זו צורה מעניינת באופן כללי - בתורת הגרפים היא אחד משני הגרפים הבסיסיים ביותר שאינם מישוריים, אבל לא אדבר על כך הפעם.

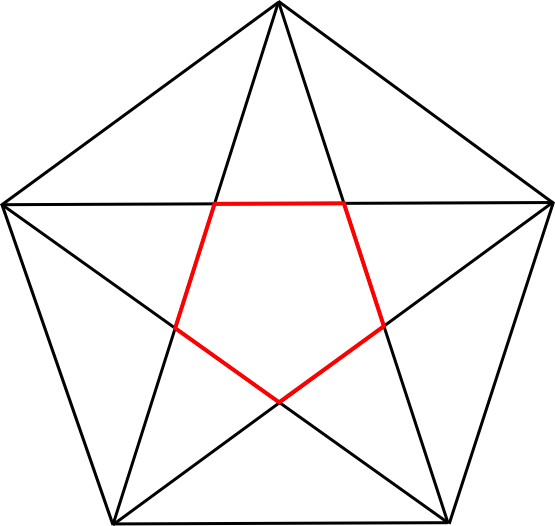
עכשיו, אם נסתכל בתוך הפנטגרמה, נראה שמתחבא בתוכה מחומש משוכלל קטן יותר, הפוך:

אבל אם קיבלנו מחומש משוכלל, אפשר למתוח את האלכסונים שלו, ולקבל עוד פנטגרמה:

וכפי שאתם מנחשים, אפשר להמשיך את התהליך הזה עד לאינסוף - בונים מחומש, ובתוכו פנטגרמה, ובתוכה מחומש, ובתוכו פנטגרמה, ובתוכה מחומש… ובכל פעם נקבל מחומשים ופנטגרמות קטנים יותר ויותר. זה יהיה רעיון המפתח בהוכחה שלנו.

בואו נסתכל לרגע על אחד מהמשולשים שמופיעים בתוך המחומש-עם-פנטגרמה:

זה בבירור משולש שווה שוקיים, שאורך כל שוק בו הוא אורך צלע הפנטגרמה - בואו נסמן אותה ב-\( A \), ואורך הבסיס שלו הוא אורך צלע המחומש - בואו נסמן אותה ב-\( B \). בכל מחומש-עם-פנטגרמה שנצייר, היחס \( \frac{A}{B} \) בין אורך צלע הפנטגרמה ואורך צלע המחומש יהיה זהה (זה נובע מדמיון משולשים על המשולש שציירתי למעלה). כעת יש שתי שאלות: מהו היחס הזה, והאם הוא מספר רציונלי? לשאלה מהו היחס הזה אחזור בסוף הפוסט; כרגע אני רוצה לשכנע אתכם שהוא מספר אי רציונלי, כלומר שלא ניתן לתאר אותו על ידי מנה של שני מספרים שלמים.

הצעד הראשון הוא לשים לב לאבחנה הפשוטה הבאה: הטענה שהיחס \( \frac{A}{B} \) הוא רציונלי שקולה לטענה שאפשר לצייר מחומש-עם-פנטגרמה באופן כזה שגם אורך צלע הפנטגרמה וגם אורך צלע המחומש שניהם מספרים טבעיים. כיוון אחד הוא ברור - אם נצליח לצייר מחומש-עם-פנטגרמה שכזה, אז \( A \) יהיה מספר טבעי וגם \( B \) יהיה מספר טבעי ולכן \( \frac{A}{B} \) יהיה מספר רציונלי. הכיוון השני פחות מיידי: אם \( \frac{A}{B} \) הוא רציונלי זה לא אומר ש-\( A,B \) הם שלמים בהכרח - הביטו למשל על \( \frac{1/4}{1/2} \) (רבע חלקי חצי) ששווה למספר הרציונלי \( \frac{1}{2} \). מה שנכון הוא שאם היחס הוא מספר רציונלי, למשל \( \frac{t}{s} \) עם \( t,s \) שלמים, אז אפשר לצייר מחומש-עם-פנטגרמה כך שאורך צלעו של המחומש היא \( s \) ואורך צלעה של הפנטגרמה הוא \( t \) ולקבל מחומש-עם-פנטגרמה שאורכי צלעותיהם הם טבעיים.

מה שאני הולך להוכיח הוא שההנחה הזו - שיש מחומש-עם-פנטגרמה שאורך הצלעות של שניהם הוא מספר טבעי - היא שגויה, והתעלול פשוט ומקסים: אני אקח מחומש-עם-פנטגרמה שכזה, אצייר בתוכו את המחומש-עם-פנטגרמה הקטן יותר שמוכל בו, ואז אוכיח שאם אורכי הצלעות של המחומש-עם-פנטגרמה הגדול הם מספרים טבעיים, אז גם אורכי הצלעות של המחומש-עם-פנטגרמה הקטן יותר הם מספרים טבעיים, קטנים יותר מאלו של המחומש-עם-פנטגרמה הגדול. מכיוון שאפשר להמשיך בתהליך יצירת המחומש-עם-פנטגרמה עד לאינסוף, זה אומר שסדרת אורכי הצלעות של הפנטגרמות שנקבל בדרך תהיה סדרה אינסופית של מספרים טבעיים שהיא יורדת ממש, כלומר שכל איבר בה קטן מהקודם לו. דבר כזה הוא לחלוטין בלתי אפשרי: אם האיבר הראשון בסדרה הוא \( n \), אז אחרי לכל היותר \( n \) איברים בסדרה נגיע אל 0, וזהו; אי אפשר לרדת יותר ועדיין להישאר עם מספר טבעי.

אם כן, האתגר הטכני שלנו הוא להוכיח שאם אורכי הצלעות במחומש-עם-פנטגרמה הגדול הם טבעיים, כך גם אורכי הצלעות במחומש-עם-פנטגרמה הקטן יותר. בשביל זה צריך להפשיל שרוולים וקצת ללכלך ידיים עם פרטים טכניים לא מורכבים מדי.

ספציפית, בואו נסמן את צלע הפנטגרמה הגדולה ב-\( A \), את צלע המחומש הגדול ב-\( B \), את צלע הפנטגרמה הקטנה יותר ב-\( a \) ואת צלע המחומש הקטן יותר ב-\( b \). מה שנוכיח הוא ש-\( a=A-B \) (ולכן בפרט \( a<A \) ואכן נקבל סדרה יורדת) ו-\( b=2B-A \). בבירור אם \( A,B \) היו טבעיים שניהם, כך גם \( a,b \). עכשיו אני מציע לכם לקחת הפסקה מהפוסט, עכשיו משאתם יודעים מה אנחנו מנסים להוכיח, ולנסות להוכיח את זה בעצמכם. גם אם לא תצליחו, המשך הפוסט יהיה כנראה קל יותר לקריאה אחרי שחשבתם קצת על זה עצמאית.

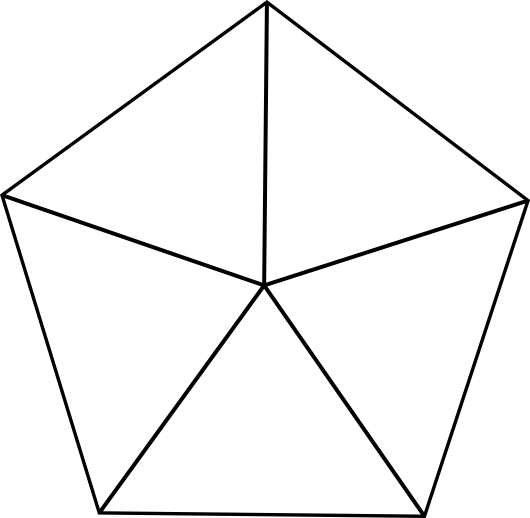
בואו נתחיל עם שאלה פשוטה: במחומש משוכלל כל הזוויות שוות, כבר אמרנו, אבל לכמה שווה כל זווית? דרך פשוטה לגלות זאת היא לפרק את המחומש לחמישה משולשים:

בגלל הסימטריה של המחומש אנחנו יודעים שכל המשולשים זהים, ושהם כולם שווי שוקיים, ולכן גם זוויות הבסיס שלהם שוות. מהי זווית הראש? סכום זוויות הראש של כל המשולשים יחד מרכיב מעגל שלם, כלומר 360 מעלות, ולכן זווית הראש היא בת \( \frac{360}{5}=72 \) מעלות. זה מותיר לשתי זוויות הבסיס \( 180-72=108 \) מעלות, ולכן כל זווית בסיס שכזו היא בת \( 54 \) מעלות. כעת, כל זווית במחומש היא סכום של שתי זוויות בסיס ולכן הזווית במחומש היא 108 מעלות.

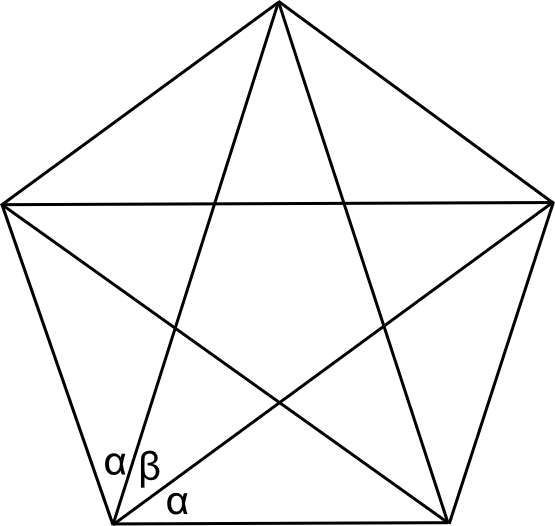
עכשיו, כל זווית של המחומש מחולקת על ידי הפנטגרמה לשלושה חלקים. שניים מהם בבירור זהים מטעמי סימטריה; בקשר לזווית האמצעית אנחנו קצת פחות בטוחים. בואו נסמן את הזוויות הצדדיות ב-\( \alpha \) ואת הזווית הפנימית ב-\( \beta \):

אז יש לנו את המשוואה \( 2\alpha+\beta=108^{\circ} \). זה לכשעצמו לא מספיק כדי לדעת מהם \( \alpha,\beta \), אבל אפשר למצוא עוד משוואה אם מסתכלים על המשולש:

זווית הראש במשולש היא \( \beta \), ואילו שתי זוויות הבסיס הן \( \alpha+\beta \). לכן נקבל את המשוואה \( \beta+2\left(\alpha+\beta\right)=180^{\circ} \), כלומר \( 2\alpha+3\beta=180^{\circ} \). קיבלנו שתי משוואות בשתי נעלמים, ואת זה קל לפתור - מחסרים את המשוואה הראשונה מהשניה ומקבלים \( 2\beta=72^{\circ} \), כלומר \( \beta=36^{\circ} \), ולכן גם \( \alpha=36^{\circ} \). כלומר, הפנטגרמה מחלקת את הזוויות של המחומש לשלושה חלקים שווים שכל אחד מהם הוא \( 36^{\circ} \). הסימטריה המושלמת הזו היא המפתח להמשך.

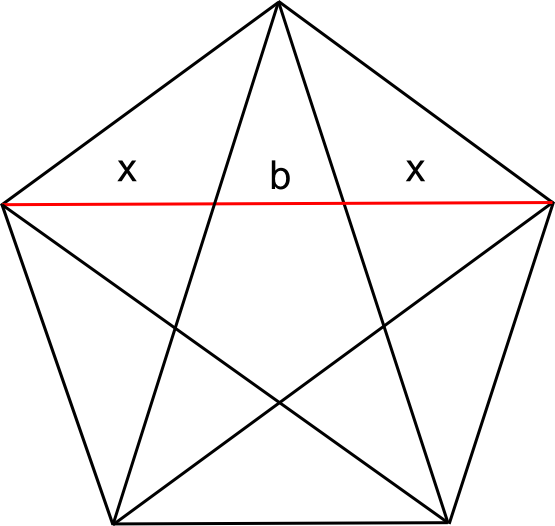
עכשיו, בואו נסתכל לרגע על צלע הפנטגרמה:

שימו לב לכך שהיא מחולקת לשלושה חלקים. אורך החלק האמצעי הוא בדיוק \( b \) - אורך צלע המחומש הקטן. מה אורך שני החלקים האחרים? מסימטריה ברור שהוא שווה; נסמן אותו \( x \). קיבלנו את המשוואה \( A=b+2x \). כמו קודם, משוואה אחת לא מספיקה לנו, אז בואו נביט במשולש הבא:

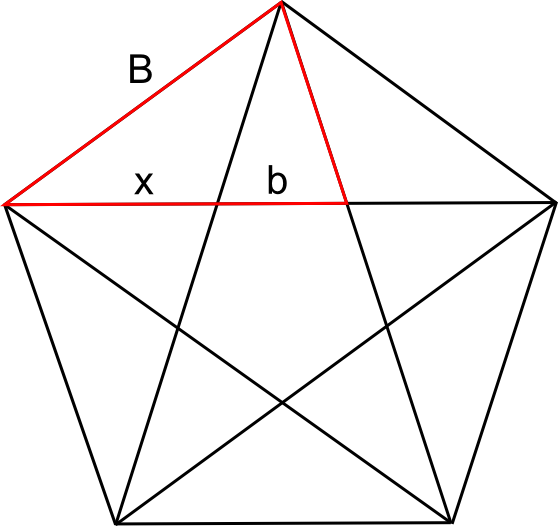
זה נראה כמו משולש שווה שוקיים, ואכן, די קל להשתכנע ששתי זווית הבסיס הן בנות 72 מעלות, בעזרת מה שכבר ראינו על הזוויות במחומש-פנטגרמה (הוכיחו זאת לעצמכם!). אחת השוקיים היא באורך \( B \) ואילו השניה היא באורך \( b+x \), כך שקיבלנו את המשוואה \( B=b+x \). נכפול את המשוואה הזו ב-2 ונחסר ממנה את הראשונה, ונקבל \( b=2B-A \), כפי שהבטחתי למעלה.

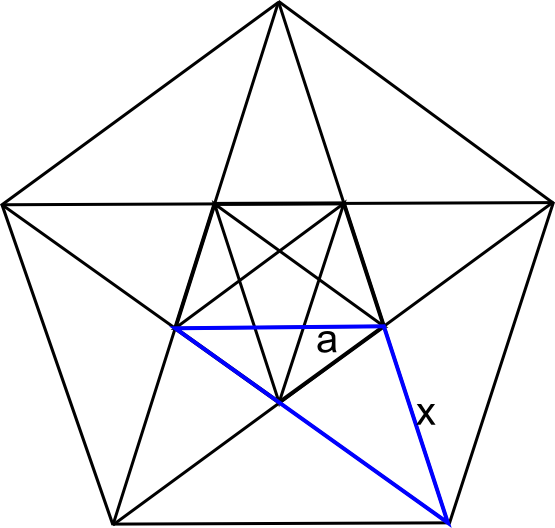
עכשיו הגיע הזמן לטפל בפנטגרמה-שבתוך-המחומש-שבתוך-הפנטגרמה. מה אורך הצלע שלה? ובכן, כבר היכרנו אותו - זה בדיוק מה שסימנתי בתור \( x \):

בציור הזה אנחנו רואים עוד משולש שווה שוקיים, שבו השוקיים הן בדיוק צלע הפנטגרמה הקטנה, והחלק של צלע הפנטגרמה הגדולה שסימנתי בתור \( x \). זוויות הבסיס של המשולש הן בנות 36 מעלות - שוב, זה נובע ממה שכבר ראינו עליהן - ולכן זה אכן משולש שווה שוקיים. המסקנה: \( A=2a+b \), אבל אנחנו כבר יודעים מהו \( b \) במונחים של \( A,B \): \( b=2B-A \). נציב ונקבל: \( 2a+2B-A=A \), כלומר \( 2a=2A-2B \), כלומר \( a=A-B \) - שוב, כמו שהבטחתי. זה מסיים את ההוכחה.

עכשיו אפשר לחזור לשאלה הנוספת. אנחנו יודעים ש-\( \frac{A}{B} \) הוא מספר אי רציונלי, אבל איזה מספר אי רציונלי? לשם כך אנסה למצוא דרך לחשב, אלגברית, את הערך של \( \frac{A}{B} \). אנחנו יודעים מדמיון משולשים שמתקיים \( \frac{A}{B}=\frac{a}{b} \) ואנחנו יודעים לבטא את \( a,b \) בעזרת \( A,B \) - זו נראית כמו נקודת פתיחה טובה. אם כן, נציב:

\( \frac{A}{B}=\frac{A-B}{2B-A} \)

עכשיו אשתמש בתעלול. באגף ימין \( A \) ו-\( B \) מופיעים לבדם וזה לא טוב לי, כי מי שמעניין אותי הוא היחס \( \frac{A}{B} \). לכן אחלק הן את המונה והן את המכנה של אגף ימין ב-\( B \), ואקבל:

\( \frac{A}{B}=\frac{\frac{A}{B}-1}{2-\frac{A}{B}} \)

כעת אסמן \( x=\frac{A}{B} \) ובואו ונראה איזו משוואה קיבלתי:

\( x=\frac{x-1}{2-x} \)

נכפול את שני האגפים ב-\( 2-x \) ונקבל:

\( 2x-x^{2}=x-1 \)

נעביר אגפים:

\( x^{2}-x-1=0 \)

למשוואה הזו יש שני פתרונות אלגבריים:

\( x_{1,2}=\frac{1\pm\sqrt{5}}{2} \)

פתרון אחד הוא שלילי ולכן חסר משמעות בשבילנו - בהכרח הפתרון האחר הוא היחס הנכון, \( \frac{1+\sqrt{5}}{2} \). זה מספר מפורסם מאוד - הוא נקרא יחס הזהב ועיקר פרסומו מגיע לו מכך שהוא צץ, לכאורה, בכל מני מקומות בטבע, באדריכלות, באסתטיקה ועוד כהנה וכהנה. התחושה שלי היא שבלא מעט מקרים שבהם “מוצאים” את יחס הזהב במקום כלשהו יש מידה לא קטנה של אילוץ ומשחק עם פרמטרים כדי שיתאימו; עם זאת, בפנטגרמה הוא מופיע באופן הכי טבעי שרק אפשר, ובתפקיד מרכזי. כמובן, אם הייתי יודע שהיחס שאני מחפש הוא יחס הזהב הייתי יכול לוותר על ההוכחה הגיאומטרית ולהסתפק בציון העובדה שהוא אי רציונלי (למשל, כי \( \sqrt{5} \) אי רציונלי), אבל שימו לב לכך שכדי לגלות שהיחס הוא יחס הזהב היה עלי לחשב אלגברית את \( a,b \) ובשלב הזה ההוכחה שלי ממילא נסתיימה. פרט לכך, אין מה לעשות - ההוכחה הגיאומטרית פשוט מגניבה יותר.