פותרים את SAT - אלגוריתם CDCL

בפוסט הקודם על פתרונות לבעיית SAT ראינו את אלגוריתם DPLL - זה היה פחות או יותר האלגוריתם הבסיסי שרוב פותרי ה-SAT המדוייקים (להבדיל מהסתברותיים) מבוססים עליו, אבל מן הסתם פותרים מודרניים הולכים רחוק יותר ממנו, ובפוסט הזה אני רוצה להציג אלגוריתם קצת יותר מודרני שמתבסס על DPLL אבל עושה עוד דברים מתוחכמים - אלגוריתם CDCL, קיצור של Conflict-Driven Clause Learning. כמובן, כמו DPLL גם זה לא “אלגוריתם” במלוא מובן המילה אלא בעיקר “מסגרת” שלתוכה אפשר לצקת שלל שיפורים ושפצורים, אבל הרעיונות הכלליים שלו עדיין מעניינים.

בואו ניזכר מה DPLL עושה, ברמה הבסיסית: הוא מבצע לסירוגין שתי פעולות שונות - הראשונה היא בחינה של הפסוק שיש לו כרגע וזיהוי השמות למשתנים ספציפיים שחייבות להתרחש, ופישוט של הפסוק לאחר ביצוע ההשמות הללו; והשניה היא בחירה של משתנה כלשהו וערך להציב בו. אם כן, יש לנו שני סוגים של השמות למשתנים: אלו שבהן בחרנו לתת למשתנה ערך מסויים - במקרה הזה, המשתנה ייקרא “משתנה בחירה” (Decision Variable), ואלו שבהן “לא הייתה לנו ברירה” והערך ששמנו במשתנה נבע מהבחירות שעשינו. כאשר האלגוריתם מזהה שהוא “נתקע” - כלומר, הוא מגלה שיש פסוקית שכבר אין לו סיכוי לספק - הוא פשוט חוזר אחורה אל משתנה הבחירה האחרון שטרם ניסינו בו את האפשרות השניה, ומנסה אותה.

המבנה של CDCL דומה אבל קצת יותר חכם. בראש ובראשונה, כאשר מתגלה ש”נתקענו” - מה שנקרא בטרמינולוגיה של האלגוריתם הזה Conflict, האלגוריתם לא סתם מתייאש ואומר “בואו נחזור אחורה” - הוא מנסה ללמוד מזה מידע כלשהו על מה שגרם לקונפליקט. את המידע שהוא לומד הוא ממדל בצורת אילוץ חדש שמוסיפים לפסוק ה-CNF שמנסים לפתור. אחר כך האלגוריתם חוזר אחורה ומבטל חלק ממשתני הבחירה האחרונים (לאו דווקא רק אחד אחורה). אספקט נחמד של האלגוריתם הוא שאין צורך לבצע “ניהול חשבונות” כדי לזכור עבור משתנה בחירה אם כבר ניסינו בו את האפשרות השניה - האילוצים שאנחנו לומדים כבר יבטיחו שלא ננסה לתת למשתנה בחירה כלשהו את אותה האפשרות פעמיים.

כל זה מאוד אבסטרקטי ולכן בואו נראה דוגמה קונקרטית, שאני גונב מה-Handbook of Satisfiability (יש דבר כזה!). פסוק \( \varphi=C_{1}\wedge C_{2}\wedge C_{3}\wedge C_{4}\wedge C_{5}\wedge C_{6} \) שמורכב מהפסוקיות הבאות:

\( C_{1}=\left(x_{1}\vee x_{31}\vee\neg x_{2}\right) \)

\( C_{2}=\left(x_{1}\wedge\neg x_{3}\right) \)

\( C_{3}=\left(x_{2}\vee x_{3}\vee x_{4}\right) \)

\( C_{4}=\left(\neg x_{4}\vee\neg x_{5}\right) \)

\( C_{5}=\left(x_{21}\vee\neg x_{4}\vee\neg x_{6}\right) \)

\( C_{6}=\left(x_{5}\vee x_{6}\right) \)

בואו נניח שבמהלך הריצה האלגוריתם שלנו הציב -\( x_{1} \) את הערך 0, ואחר כך ב-\( x_{31} \) הציב את הערך 0, ולבסוף הציב ב-\( x_{21} \) את הערך 0. מה קורה?

ובכן, ההצבה ב-\( x_{1} \) תגרום ל-\( C_{2} \) להפוך לפסוק \( \left(\neg x_{3}\right) \) כך ש-\( x_{3} \) חייב להיות 0. בדומה, \( C_{1} \) יאבד גם את \( x_{1} \) וגם את \( x_{31} \) ולכן גם \( x_{2} \) חייב להיות 0. עכשיו משני אלו נקבל ב-\( C_{3} \) ש-\( x_{4} \) חייב להיות 1, וזה יגרור ש-\( x_{5} \) הוא 0 בגלל \( C_{4} \), וש-\( x_{6} \) חייב להיות 0 על פי \( C_{5} \). אבל עכשיו “הפסדנו” את \( C_{6} \) כי שני הליטרלים שלו (החיובי והשלילי) קיבלו 0. השאלה היא מה אפשר ללמוד מזה.

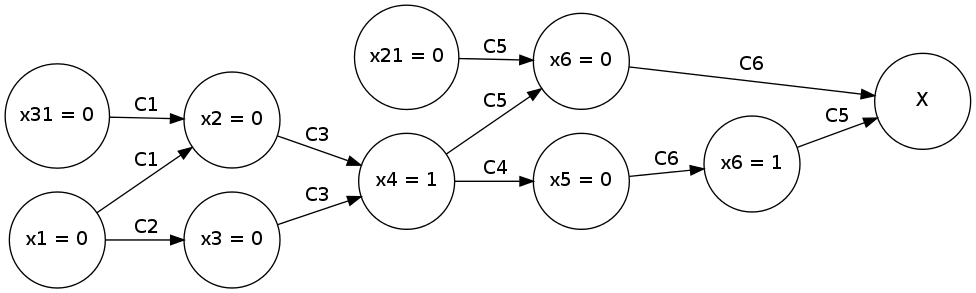
ובכן, כל המלל שלעיל הוא קצת מסורבל. קל יותר להבין מה הלך כאן אם מציירים את זה בתור גרף:

מה שיש לנו כאן מכונה Implication graph - “גרף הגרירות”. הצמתים שלו הן כל ההשמות למשתנים - הן משתני הבחירה והן המשתנים הנגררים. יש קשת מהשמה אחת להשמה אחרת אם ההשמה האחת הייתה מעורבת בגרירה של האחרת - והכיתוב של הקשת הוא הפסוקית שבה התבצעה הגרירה הזו. \( X \) מייצג את ההרס והחורבן של הסתירה שהגענו אליה - אם תרצו, אפשר לחשוב עליו כאילו הוא נגרר מפסוקית ש”התרוקנה”, או ממשתנה אחד שהושמו בו שני ערכים שונים (זו בעצם אינדיקציה לכך שיש שתי פסוקיות שמתרוקנות - אחת כשמציבים במשתנה הזה 0 והשניה שמתרוקנת כשמציבים בו 1).

פורמלית, אם \( x \) הוא משתנה אז כדי שהצומת \( x=1 \) יופיע בגרף צריכה להיות ב-\( \varphi \) פסוקית מהצורה \( \left(l_{1}\vee\dots\vee l_{k}\vee x\right) \) כך ש-\( l_{1},\dots,l_{k} \) קיבלו כולם את הערך 0 בהשמה למשתנים שלהם, ואז מהצמתים של ההשמות הללו תהיה קשת אל הצומת \( x=1 \). הסיפור עבור \( x=0 \) דומה רק שהפסוקית צריכה להיות מהצורה \( \left(l_{1}\vee\dots\vee l_{k}\vee\neg x\right) \).

הצמתים היחידים בגרף שאין להם אב הם הצמתים שמייצגים השמות למשתני החלטה (כי ההשמות הללו לא נגררו משום דבר). כמובן, בפסוק ענקי עשוי להיות גרף גרירות ענקי, ורובו לאו דווקא יהיה רלוונטי בכלל לקונפליקט שאליו הגענו בסוף. לכן נהוג להצטמצם לתת-גרף (“גרף הקונפליקט”) שבו “מגלחים” את החלק המיותר - אם ל-\( X \) יש יותר ממשתנה אחד שגורר אותו (יש קונפליקט בכמה משתנים) מתמקדים רק בצמתים של משתנה אחד, והולכים ממנו אחורה תוך שלוקחים רק את מה שחייבים: לכל צומת בוחרים פסוקית אחת ולוקחים את כל הצמתים שנכנסים אליו והקשתות שלהם מסומנות בפסוקית הזו, עד שמגיעים בכל מקום לצמתים של השמות למשתני בחירה.

כמובן, האופן שבו בוחרים איך בדיוק לצמצם גרף גרירה כללי לתת-גרף הקונפליקט הזה הוא עניין לאינסוף היוריסטיקות שיכולות להשפיע באופן דרסטי על איכות הפותר. אבל אני לא מבין בזה יותר מדי ולא אכנס לזה עכשיו.

נניח שיש לנו גרף קונפליקט ואנחנו רוצים ללמוד ממנו משהו. מה נעשה עכשיו? אם נחשוב על זה לרגע, ברור שכל קשת בגרף הזו קריטית - אם נעיף אחת מהקשתות, הגרירות של הגרף כבר לא יתקיימו והקונפליקט לא יתרחש. איך מעיפים קשת? “לומדים” פסוקית חדשה שמחסלת את ההשמה שהקשת יצאה ממנה. למשל, נניח שאנחנו רוצים לחסל את הקשת שיוצאת מ-\( x_{5}=0 \). אנחנו יכולים להוסיף לפסוק שלנו את הפסוקית \( \left(x_{5}\right) \) שמכריחה את \( x_{5} \) להיות 1, ובכך נמנע את הקונפליקט. הבעיה היא שזו גישה חזקה מדי - אנחנו נסגרים על הערך שניתן ל-\( x_{5} \) מכאן ואילך, ולא חושבים שאולי פספסנו אפשרויות שבהן \( x_{5} \) עדיין יקבל 0 והפסוק יסתפק (וזה בעייתי מאוד כי באופן כללי ייתכן שיש השמה כזו, אבל אין השמה שבה \( x_{5} \) מקבל 1 והפסוק מסתפק).

אז אפשר ללכת לקיצוניות השניה: אפשר לומר שצריך להיפטר מקשת כלשהי בגרף, ולהוסיף פסוקית שאומרת שלפחות אחת מההשמות שמופיעות בגרף, חוץ מ-\( x_{6}=1 \), היא פסולה: \( \left(x_{31}\vee x_{1}\vee x_{2}\vee x_{3}\vee\neg x_{4}\vee x_{21}\vee x_{5}\vee x_{6}\right) \). למה חוץ מ-\( x_{6}=1 \)? כי כבר אמרנו ש-\( x_{6}=0 \) פסול, ואם נאמר שגם \( x_{6}=1 \) פסול נכסה בכך את כל האפשרויות מבלי לומר משהו מעניין חדש, כי כל השמה פוסלת את \( x_{6}=0 \) או את \( x_{6}=1 \).

הבעיה היא שהפסוקית הזו בבירור גדולה מדי - אנחנו יכולים להיות יותר ממוקדים מזה. אז מה הסוד? לוקחים חתך בגרף.

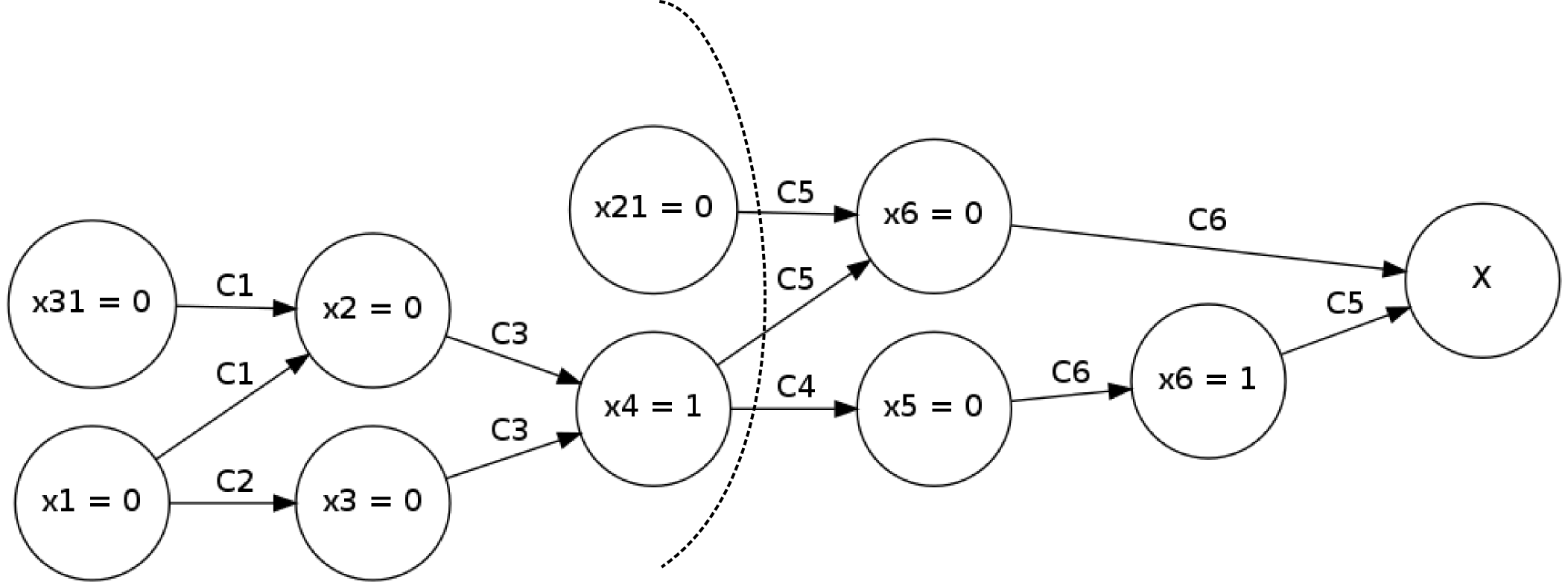
אינטואיטיבית, חתך הוא קטיעה של קשתות בגרף כך שהגרף יתפרק לשני חלקים. פורמלית, חתך הוא פשוט חלוקה של צמתי הגרף לשתי קבוצות, ונהוג לדבר על הקשתות שחוצות את החתך - כל הקשתות שקצה אחד שלהן הוא בקבוצה אחת של החתך והקצה השני בקבוצה השניה. הנה דוגמה לחתך בגרף שלנו:

אז אנחנו לוקחים חתך שמקיים את התכונה הבאה: בקבוצה האחת שלו יש את כל משתני ההחלטה, ובקבוצה השניה יש לפחות אחד מהמשתנים שגרם לקונפליקט, ואת הצומת \( X \). נסתכל על הקשתות שחוצות את החתך, ובאופן יותר ספציפי - בצמתים שמהם הקשתות יצאו. לא קשה במיוחד להשתכנע שאם יש לנו השמה כלשהי שמתאימה להשמות שכתובות בצמתים הללו, אז בהכרח נגיע לקונפליקט (בלי קשר לשאלה מה ההשמה עושה לשאר הצמתים). אז בכל השמה שמספקת את הפסוק, לפחות אחת מההשמות הללו חייבת להשתנות. המשמעות של זה עבור החתך הספציפי שבחרנו הוא הוספת הפסוקית הבאה לפסוק:

\( \left(\neg x_{4}\vee x_{21}\right) \)

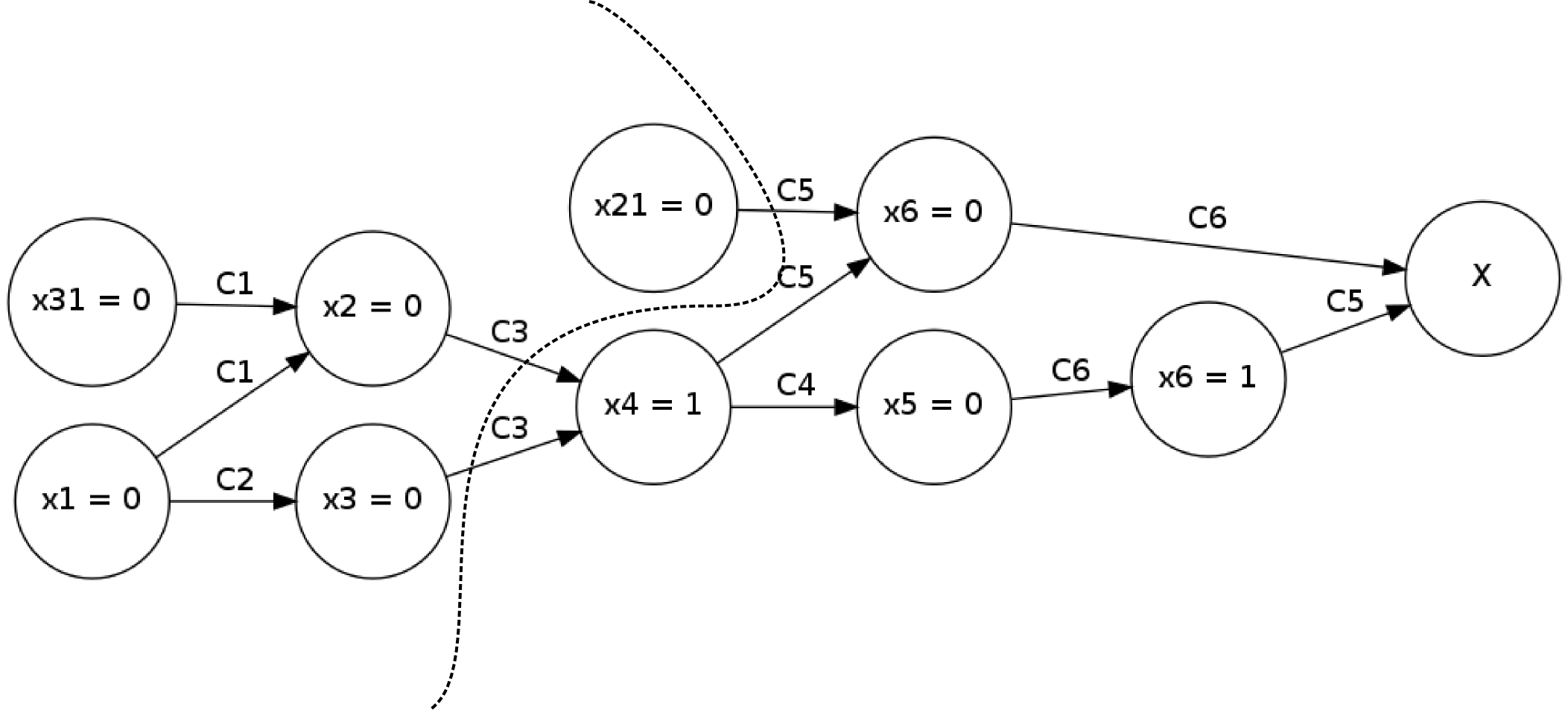
זה כמובן הרבה יותר פשוט (ומצמצם יותר את מרחב החיפוש של אלגוריתם ה-CDCL) מאשר הפסוקית המפלצתית שתיארתי קודם. אבל זו לא האפשרות היחידה, כמובן; הנה חתך שנותן לנו את הפסוקית \( \left(x_{21}\vee x_{2}\vee x_{3}\right) \):

ושוב, איך מחליטים איזה חתך לקחת? אין לי תשובה נחמדה - היוריסטיקות, היוריסטיקות, היוריסטיקות. ודברים קצת יותר חכמים שאני לא הולך להיכנס אליהם עכשיו.

חזרה לאלגוריתם ה-CDCL שלנו. אחרי שהאלגוריתם נתקל בקונפליקט, הוא מביט בגרף קונפליקט עבורו, בוחר חתך, מוסיף פסוקית לפסוק שלו, ואז קופץ חזרה אחורה - כלומר, מבטל חלק ממשתני הבחירה (לא מחליף את ערכם; פשוט שוכח שאי פעם הושם בהם ערך).

לצורך כך, גרף הגרירות צריך להכיל עוד פריט מידע שלא כתבתי בו כי זה כבר היה מסרבל: לכל השמה צריך להוסיף את דרגת ההחלטה שלה. דרגת החלטה של צומת החלטה היא קלה: היא שווה לדרגת ההחלטה של צומת ההחלטה הקודם, ועוד 1. עבור צמתים אחרים, דרגת ההחלטה שלהם היא המקסימלית מבין דרגות ההחלטה של הצמתים שנכנסים אליהם (מכיוון שרק אחרי שכל ההשמות הללו בוצעו ערכו של הצומת נקבע). כעת, אחרי שהחלטנו איזו פסוקית להוסיף, אנחנו מסתכלים על דרגות ההחלטה של הליטרלים שבפסוקיות - אם נלך אחורה ונבטל את כל ההחלטות עד וכולל דרגת ההחלטה הגבוהה ביותר של ליטרל בפסוקית, הפסוקית “תיכנס לפעולה”.

בואו נסתכל על הדוגמה שלנו לשם כך. אצלנו דרגת ההחלטה של \( x_{1} \) היא 0, של \( x_{31} \) היא 1 ושל \( x_{21} \) היא 2. מה זה אומר על ההשמות הנגזרות? \( x_{3}=0 \) היא מדרגה 0 (נובעת רק מ-\( x_{1}=0 \)) ו-\( x_{2}=0 \) היא מדרגה 1, ולכן \( x_{4}=1 \) היא מדרגה 1, ולכן \( x_{5}=0 \) היא מדרגה 1 וכך גם \( x_{6}=1 \), ואילו \( x_{6}=0 \) היא מדרגה 2. נניח עכשיו שאנחנו לוקחים חתך שיוסיף לנו את הפסוקית \( \left(x_{2}\vee x_{3}\right) \). אם עכשיו נחזור רק צעד אחד אחורה בזמן ונבטל את ההשמה של דרגה 2, כלומר את \( x_{21}=0 \), זה לא יבטל את ההצבה של 0 ב-\( x_{2},x_{3} \) ונישאר תקועים עם פסוקית שלא הסתפקה. אז יש לנו שתי אפשרויות: או לבטל גם את ההשמה בדרגה 1, כלומר את \( x_{31}=0 \), מה שיבטל את ההשמה \( x_{2}=0 \); או לבטל אפילו את ההשמה בדרגה 0.

במקרה הראשון, נקבל ש-\( x_{3}=0 \) עדיין מתקיים, ולכן הפסוקית \( \left(x_{2}\vee x_{3}\right) \) תהפוך ל-\( x_{2} \); במילים אחרות, ההצבה של דרגה 0, זו של \( x_{1}=0 \), תגרור ש-\( x_{2}=1 \). ואז יקרה משהו מעניין - אם תסתכלו על הפסוקית \( C_{1} \), תראו שאחרי ההשמה הזו, נהיה חייבים להציב \( x_{31}=1 \). במילים אחרות, הוספת הפסוקית \( \left(x_{2}\vee x_{3}\right) \) וחזרה אחורה עד לביטול לדרגה 1 גרמה לכך ש-\( x_{31} \) כבר לא יהיה משתנה בחירה אלא משתנה נגזר, והערך שאנחנו מציבים בו יהיה הפוך מהערך שהצבנו בו כשהוא היה משתנה בחירה והגענו לסתירה. בקיצור, זה עובד!

במקרה השני, יש לנו משחק חדש - הפסוקית \( \left(x_{2}\vee x_{3}\right) \) לא תגרום לשום דבר להתרחש מייד. אבל היא תהיה חלק מהפסוק שלנו, ופעפועים עתידיים הולכים להתחשב בה.

אם כן, זהו הרעיון הכללי שמאחורי “למידת פסוקיות”. לי הרעיון הזה נשמע פשוט יחסית, וזה מאוד מפתיע ששיטות כאלו הן כל כך יעילות (יחסית). אבל בזכות היעילות הגבוהה שלהן, פותרי SAT הם שימושיים מאוד בפתרון בעיות אמיתיות; בפוסט הבא אתחיל להציג דוגמה לתחום שכזה.