המחט של בופון
היום חל “יום פאי”, כלומר תאריך היום הוא ה-14/3, שבארצות פחות מתוקנות נכתב כ-3.14, כלומר כמו התחלת הפיתוח העשרוני של הקבוע \( \pi \), פאי (היחס בין היקף מעגל לקוטרו בגאומטריה האוקלידית) - ומכאן, תירוץ לחגוג ולאכול פאי עם פאי.
מבחינתי זה תירוץ לכתוב פוסט על משהו שבו מופיע \( \pi \), ורצוי משהו קליל יחסית. דוגמה נפלאה ל”משהו” כזה שטרם הופיע בבלוג בשום צורה היא בעיית המחט של בופון. בפשטות, הבעיה אומרת את הדבר הבא: יש לנו מחברת שורות ואנחנו זורקים עליה מחט. מה ההסתברות שהמחט תיפול על קו מפריד כלשהו במחברת?
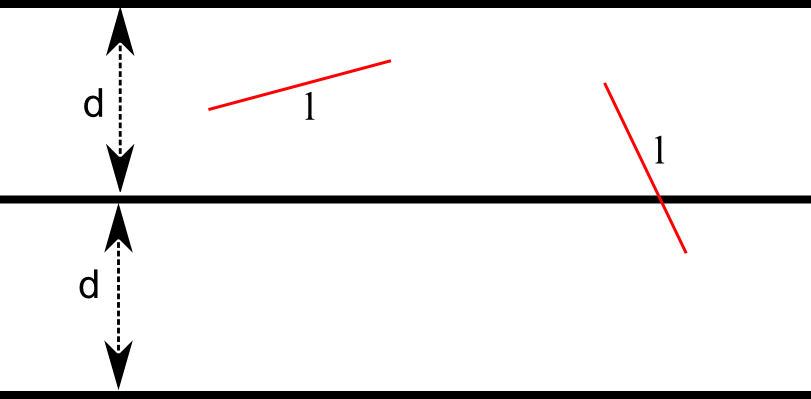
ברור שהשאלה הזו תלויה בשני פרמטרים - אורך המחט, והרוחב של כל שורה (דהיינו, מה המרחק בין כל שני קווים מפרידים של שורות). נסמן את אורך המחט ב-\( l \) ואת הרוחב של שורה ב-\( d \). בציור הבא אפשר לראות את השורות ברוחב \( d \) ושני מחטים באורך \( l \), שאחת מהן לא נפלה על אף קו מפריד, ואחת כן נפלה:
קל להגיע למסקנה שיש הבדל כלשהו בין הסיטואציה שבה \( l>d \), כלומר המחט גדולה מרוחב שורה ולכן אם היא נופלת בזווית שמאונכת לקווים המפרידים היא על בטוח חוצה קו מפריד שכזה, ובין הסיטואציה שבה \( l\le d \). אני הולך לדבר רק על הסיטואציה השניה, מהטעם הפשוט שהנוסחה יוצאת הרבה יותר פשוטה ונחמדה בה, והרעיון עבור \( l>d \) הוא אותו רעיון, עם עוד פרטים טכניים.
איך זה קשור לפאי? פשוט מאוד - התשובה הולכת לערב את פאי איכשהו, למרות שאין לו רמז בניסוח השאלה, ואפילו אין בשאלה מעגלים (מעגלים הם המקור הטבעי לפאי). אז מאיפה פאי הגיע? נראה די מהר שבאופן די טבעי אפשר לערב מעגלים בשאלה ואפילו כדאי, ושפאי מגיע מהם.
אני רוצה להראות בפוסט הזה שני פתרונות לבעיה. הראשון יהיה שימוש סטנדרטי בחשבון אינפיניטסימלי - מסוג הדברים שסביר לתת לסטודנטים להסתברות לעשות. במילים אחרות, זה יהיה פתרון נכון ופשוט, אבל הוא לא יהיה כל כך מעניין. הפתרון השני הוא מגניב משמעותית מהראשון וגם נלמד עוד דברים מתוך ההוכחה שלו, אבל אני מעדיף “להוציא מהמערכת” את הפתרון הסטנדרטי קודם כל. למי שלא מתעניין בפתרון הזה או שהפרטים הטכניים מרתיעים אותו - פשוט תקפצו מעליו, לא אכפת לי. אני אשב עם האינטגרל שלי לבד, בחושך. הכל בסדר.
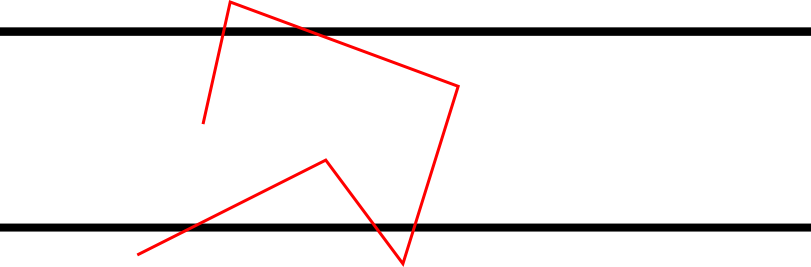
אוקיי, אז מה עושים? ראשית כל צריך לחדד עניינים כמו מה מרחב ההסתברות שלנו וכדומה. כשאנחנו “זורקים” מחט, מה אנחנו בעצם מגרילים? שני דברים - את הזווית שלה (ביחס לציר \( x \), כפי שבדרך כלל מחשבים זווית של ישרים) ואת המיקום שלה. אני אסתכל על אחת מהקצוות של המחט בתור ה”ראשית” שלה, והמיקום של המחט יהיה המיקום של הראשית הזו. הזווית תימדד ביחס לסיבוב שבו משאירים את הראשית קבועה (כלומר, מסובבים את המחט סביב הראשית ובודקים כמה סיבוב עם כיוון השעון נדרש כדי “להחזיר” אותה למצב שבו היא מתלכדת עם ציר \( x \)). לא קשה לראות שהמיקום האופקי של המחט, או השאלה באיזו שורה במחברת הראשית של המחט נפלה, הן חסרות חשיבות - כל מה שחשוב הוא הזווית, שהיא מספר \( 0\le\theta\le2\pi \) (הנה פאי!) והגובה של הראשית מעל הקו המפריד התחתון בשורה, \( 0\le h\le d \). הנה ציור שמבהיר את זה:
המספרים \( \theta,h \) הללו נבחרים בהתפלגות אחידה מתוך התחומים שלהם. לכן (מנימוקים סטנדרטיים בהסתברות), ההסתברות שהמחט תחצה קו מפריד היא בדיוק היחס בין שטח של קבוצת כל הנקודות \( \left(\theta,h\right) \) שעבורן המחט חוצה קו מפריד ובין השטח של כל הנקודות \( \left(\theta,h\right) \) הרלוונטיות בכלל. אם כן, נשאלת השאלה: בהינתן \( \theta \), מה הערכים של \( h \) שעבורם יש חצייה?
ובכן, בהינתן \( \theta,h \), השאלה היא מה גובה הקצה של המחט שאינו הראשית. התשובה היא שימוש סטנדרטי בטריגונומטריה: \( h+l\sin\theta \).
כאשר \( \theta>\pi \) הגובה הוא נמוך יותר מאשר \( h \). כדי לחסוך לעצמי פירוק למקרים, פשוט אצביע על כך שהמקרה הזה סימטרי למקרה של \( 0\le\theta\le\pi \) ולכן מעכשיו אסתפק בהנחה ש-\( 0\le\theta\le\pi \). במקרה זה, על מנת שהמחט תחצה קו מפריד, צריך להתקיים \( h+l\sin\theta>d \) (אגב, כל הדיבורים על “לחצות” את הקו המפריד מיותרים - גם אם נרשה למחט לגעת בלי לחצות החישובים שלנו לא ישתנו, מכיווון שההסתברות של כל מאורעות ה”נגיעה” הללו היא אפס - אין להם “שטח” - אבל נעזוב את זה). במילים אחרות, צריך להתקיים \( h>d-l\sin\theta \). מכאן אנחנו מקבלים את החישוב הבא של שטח קבוצת כל הנקודות שעבורן יש חציה:
\( \int_{0}^{\pi}\left(\int_{d-l\sin\theta}^{d}dh\right)d\theta=\int_{0}^{\pi}\left(d-\left(d-l\sin\theta\right)\right)d\theta=l\int_{0}^{\pi}\sin\theta d\theta=l\left(-\cos\pi+\cos0\right)=2l \)
והשטח של קבוצת כל הנקודות הרלווניטות הוא שטח המלבן שאורכי צלעותיו \( \pi \) ו-\( d \), כלומר \( d\pi \). בסך הכל אנחנו מקבלים את הנוסחה \( \frac{2}{\pi}\frac{l}{d} \) - וזו אכן הנוסחה הנכונה. לא קשה לראות שהחישוב הזה נשבר אם \( d<l \) וזה תרגיל טוב למצוא את הנוסחה במקרה הזה, אבל היא יוצאת מזעזעת, כאמור, וחבל.
אוקיי, אז סיימנו עם הפתרון הפשוט, ועכשיו אפשר לדבר בשקט על הפתרון המסובך בלי שאף אחד מהקהל יציץ וישאל “אבל למה לא פתרת עם אינטגרלים וזהו?!”. אני רוצה לפתור בלי אינטגרלים כי הפתרון המסורבל יותר הוא פשוט יותר יפה ומהנה.
לפני שאציג אותו, קוריוז חביב שקשור לנוסחה שכבר מצאנו. כפי שאנחנו רואים, \( \pi \) נמצא בנוסחה הזו בצורה פשוטה מאוד. זה מצביע על כך שאם נצליח, עבור \( l,d \) נתונים, לחשב מספרית את ההסתברות לכך שהסיכה תחצה קו, נוכל לקבל מכך קירוב של פאי. איך אפשר לבצע את החישוב הזה? ובכן, פשוט תזרקו סיכות ותראו מה קורה! לטכניקת חישוב הסתברותית שכזו קוראים “שיטת מונטה-קרלו” (אין שיטה ספציפית שנקראת “מונטה-קרלו”; זה שם כללי להרבה שיטות חישוב שונות). בשנת 1901, מתמטיקאי בשם לזאריני טען שהוא באמת עשה את זה - השליך סיכות על מחברת וספר בכמה פעמים הסיכה נפלה על הקו. הוא זרק 3408 סיכות, כך ש-\( \frac{l}{d} \) היה \( \frac{5}{6} \), ומצא שבדיוק ב-1808 מהפעמים הסיכות נפלו על הקו. אז מה הקירוב של פאי שנקבל כאן? \( \frac{2}{\pi}\frac{5}{6}\approx\frac{1808}{3408} \), כלומר
\( \pi\approx\frac{10}{6}\cdot\frac{3408}{1808}=\frac{355}{113}=3.1415929\dots \)
זה קירוב די פנטסטי. למעשה, פנטסטי מדי. \( \frac{355}{113} \) הוא הקירוב הטוב ביותר לפאי באמצעות מספר רציונלי עם מונה ומכנה קטנים (הקירוב המפורסם האחר הוא \( \frac{22}{7} \) שגם הוא מצויין אבל פחות טוב). זה מתחיל להסביר לנו למה לזאריני הטיל סיכה בדיוק 3408 פעמים - מספר מוזר ולא עגול לכל הדעות - ולמה הוא בחר את \( l,d \) בצורה שנותנת \( \frac{l}{d}=\frac{5}{6} \) הוא ניסה להנדס את הקירוב \( \frac{355}{113} \)!
בואו נראה את זה מתמטית. אם \( p \) היא ההסתברות להפיל מחט על קו מפריד, אז \( \frac{2}{\pi}\frac{l}{d}=p \), כלומר \( \pi=\frac{2}{p}\frac{l}{d} \). אם אנחנו רוצים לקבל את הקירוב \( \pi\approx\frac{355}{113} \), אנחנו צריכים שיתקיים \( \frac{355}{113}=\frac{2l}{d}\cdot\frac{T}{a} \), כאשר \( T \) הוא מספר הנסיונות הכולל שלנו ו-\( a \) הוא מספר ההצלחות. עכשיו, מספר ההצלחות הוא תמיד מספר שלם, וצריך להתקיים \( a=\frac{113}{355}\cdot\frac{2l}{d}T \) - שוויון ממש! במילים אחרות, הסיכוי לקבל את הקירוב הנפלא הזה ל-\( \pi \) הוא רק אם \( a \) יוצא “בסדר” כאשר \( T \) כפול \( \frac{113}{355}\cdot\frac{2l}{d} \) יוצא מספר שלם. לכן, אם לזאריני רוצה לעבוד כמה שפחות קשה, הוא רוצה לבחור את \( \frac{113}{355}\cdot\frac{2l}{d} \) בצורה שבה המכנה יהיה קטן. \( 355=5\cdot71 \) ולכן מתבקש לבחור \( l=5 \) כדי לנטרל את ה-5 שב-355. נקבל \( \frac{113}{71}\cdot\frac{2}{d} \). אנחנו חייבים לבחור את \( d \) להיות גדול מ-\( l \), וככל שהוא יותר גדול כך זה מקשה עלינו יותר, אז נבחר \( d=6 \) ונקל \( \frac{113}{71}\cdot\frac{1}{3}=\frac{113}{213} \).
מה יוצא מכל זה בפועל? שעל כל 213 השלכות סיכה שלזאריני מבצע, יש לו סיכוי לקבל את הקירוב הנפלא \( \frac{355}{113} \) לפאי, אם רק יתמזל מזלו ויתקיים שב-\( T \) השלכות הסיבה שבוצעו עד כה, בדיוק \( \frac{113}{213}T \) מההשלכות נפלו על הקו. כעת, \( \frac{3408}{213}=16 \), כלומר ללזאריני היו 16 “הזדמנויות” כאלו לפני שהוא קיבל את מבוקשו, ואז הפסיק מייד (כל השלכה נוספת הייתה מקלקלת לו את הקירוב הנפלא). זה כמובן מסביר את המספר המוזר והלא עגול \( 3408 \) ואת הבחירה של \( l,d \). לטעמי לזאריני אמנם יצא רמאי, אבל רמאי משעשע והניתוח של הרמאות שלו הוא מהנה, אז אני שמח שהוא רימה ככה.
כעת בואו נעבור לפתרון היפה יותר לבעיית המחט. הרעיון הוא לפתור בעיה כללית יותר: אנחנו זורקים מחט מאורך \( l \) כלשהו (גם \( l>d \)) בצורה אקראית ושואלים כמה קווים המחט הולכת לחתוך. במילים אחרות, אנחנו מגדירים משתנה מקרי \( X \) שסופר את החיתוכים של המחט עם הקווים המפרידים, ותוהים מה התוחלת של המשתנה הזה, \( E\left[X\right] \). פתרון כללי לשאלה הזו נותן גם פתרון כללי לשאלת ההסתברות במקרה של \( l<d \), מכיוון שאז מספר החיתוכים הוא או 1 או 0, כלומר המשתנה המקרי הוא מה שנקרא אינדיקטור והתוחלת שלו שווה להסתברות שהוא יקבל 1.
ולמה כל כך מועיל לעבור לדבר על תוחלת? בגלל שיש לתוחלת תכונה נפלאה, קסם של ממש, שנקראת לינאריות. אם \( X,Y \) הם שני משתנים מקריים, אז מתקיים \( E\left[X+Y\right]=E\left[X\right]+E\left[Y\right] \), וזה נכון גם אם המשתנים תלויים הסתברותית.
איך ננצל את תכונת התוחלת הזו? על ידי התעלול הבא: נניח שאנחנו זורקים מחט באורך \( l \) באקראי, אבל חושבים על המחט בתור שתי מחטים ש”הודבקו” אחת לשניה - מחט אחת מאורך \( x \) והמחט השניה מאורך \( y \). אז \( E\left[l\right]=E\left[x+y\right]=E\left[x\right]+E\left[y\right] \) (כאן אני עושה מה שמכונה Abuse of notation - אני כותב את אורכי המחטים במקום לטרוח ולכתוב שמות של משתנים מקריים שמייצגים את המחטים מהאורך הזה).
אז מה קיבלנו? תשכחו לשניה מהסתברות ותוחלות וכאלה. יש לנו פונקציה \( f \) שמוגדרת על כל הממשיים החיוביים, ומקיימת \( f\left(x+y\right)=f\left(x\right)+f\left(y\right) \). משוואה כזו נקראת משוואה פונקציונלית, כי הנעלם בה הוא בכלל \( f \) - אנחנו מבקשים לדעת אילו פונקציות \( f \) הן פתרון למשוואה הזו. המשוואה הספציפית הזו היא מפורסמת - היא נקראת “המשוואה הפונקציונלית של קושי”. בעבר כבר הראיתי בבלוג איך פותרים משוואה פונקציונלית דומה (“המשוואה הפונקציונלית האקספוננציאלית של קושי), המשוואה \( f\left(x+y\right)=f\left(x\right)\cdot f\left(y\right) \). טכניקת הפתרון כאן היא דומה:
ראשית, שימו לב לכך ש-\( f\left(2x\right)=f\left(x\right)+f\left(x\right)=2f\left(x\right) \). כעת תעשו אותו דבר עם \( n \) עותקים של \( x \) ותקבלו \( f\left(nx\right)=nf\left(x\right) \) לכל \( n \) טבעי (אפשר להוכיח פורמלית באינדוקציה). השלב הבא הוא לשים לב לכך ש-\( f\left(x\right)=f\left(\frac{x}{m}+\dots+\frac{x}{m}\right)=mf\left(\frac{x}{m}\right) \), אז קיבלנו \( f\left(\frac{x}{m}\right)=\frac{1}{m}f\left(x\right) \). על כן, \( f\left(\frac{n}{m}x\right)=nf\left(\frac{1}{m}x\right)=\frac{n}{m}f\left(x\right) \), או במילים אחרות - \( f\left(rx\right)=rf\left(x\right) \) לכל \( r \) רציונלי. אם נסמן \( f\left(1\right)=c \), אז קיבלנו \( f\left(r\right)=f\left(1\cdot r\right)=rf\left(1\right)=cr \) לכל \( r \) רציונלי. מה קורה עם מספרים אי רציונליים? באופן כללי צריך עוד הנחה על האופי של \( f \).
במקרה שלנו אנחנו יודעים ש-\( f \) היא מונוטונית, כלומר מקיימת שאם \( x<y \) אז \( f\left(x\right)\le f\left(y\right) \) (למה? כי במקרה שלנו, אם \( x<y \) אז \( y=x+z \) כאשר גם \( z \) חיובי, ואז \( E\left[y\right]=E\left[x+y\right]=E\left[x\right]+E\left[z\right]\ge E\left[x\right] \)). זה מסיים את הסיפור לכל \( x \) ממשי ומוכיח ש-\( f\left(x\right)=cx \). שכן אפשר לקחת שני רציונליים \( r_{1},r_{2} \) כך ש-\( r_{1}<x<r_{2} \) והם קרובים ל-\( x \) כרצוננו, ויתקיים \( f\left(r_{1}\right)\le f\left(x\right)\le f\left(r_{2}\right) \), דהיינו \( cr_{1}\le f\left(x\right)\le cr_{2} \). כאשר \( r_{1} \) ו-\( r_{2} \) שואפים ל-\( x \), הביטויים משמאל ומימין שואפים ל-\( cx \) ולכן הפונקציה באמצע שואפת ל-\( cx \) גם כן (“כלל הסנדוויץ’”).
אם לחזור למחט של בופון, קיבלנו ש-\( E\left[l\right]=c\cdot l \). רק נותר להבין מיהו \( c \) המדובר. אנחנו כבר יודעים שהוא אמור להיות \( c=\frac{2}{\pi d} \), אבל איך מגיעים אל זה?
כאן מגיע הקסם הנפלא, שבזכותו ההוכחה הזו כל כך אדירה. כבר ראינו קודם שמחט ארוכה אפשר לקחת ולחשוב עליה כעל שתי מחטים קטנות יותר “דבוקות” זו לזו - כל מה שחשוב הוא שסכום אורכי המחטים הוא אורך המחט המקורית. הנקודה היא שאפשר לעשות את זה גם בצורה קיצונית יותר - גם אם המחט שלנו היא לא קו ישר אלא אוסף של קווים ישרים מחוברים - “עקום פוליגונלי”. למשל זה:
זה לא משנה איך ה”מחטים” שמהם מורכב העקום מחוברות זו לזו - כל מה שחשוב הוא סכומי האורכים שלהן. אפשר לחשוב על ניסוי השלכת הצורה הפוליגונלית על המחברת בתור אוסף של השלכות של כל המחטים האינדיבידואליות; כמובן, בגלל שהמחטים דבוקות זו לזו אז הניסויים הללו תלויים מבחינה הסתברותית, אבל כבר אמרתי שהקטע עם “התוחלת היא סכום התוחלות” לא מושפע מזה.
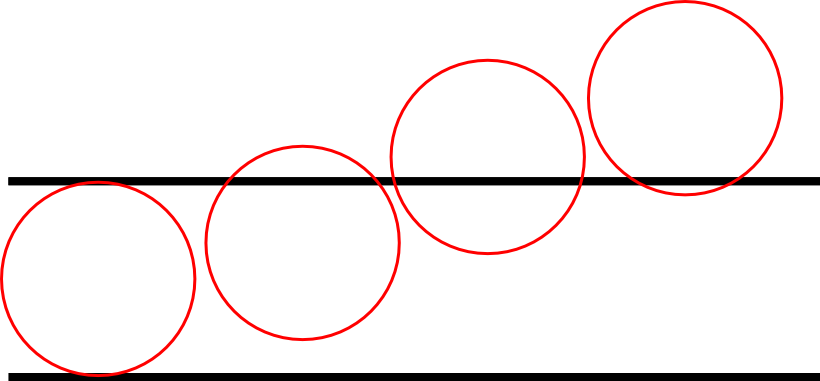
ועכשיו הפאנץ’: בואו ניקח בתור ה”מחט” שלנו מעגל. כמובן, מעגל הוא לא עקום פוליגונלי, אבל אפשר לקרב אותו כרצוננו עם עקומים פוליגונליים כך שכדי להוכיח את מה שאטען כרגע על מעגל רק צריך עוד קצת ביסוס טכני שלא אכנס אליו (הוא תרגיל מצויין כדי לוודא שהבנתם מה קורה פה). אז חזרה למעגל - אני אקח מעגל שקוטרו הוא בדיוק \( d \). מעגל כזה, לא משנה איך תשימו אותו, הולך להכיל בדיוק שני חיתוכים עם קווים מפרידים (שוב, ייתכן שהוא רק ישיק לשניהם, אבל זה מקרה עם הסתברות 0 ואפשר גם לדבר על “נגיעה בקווים מפרידים” במקום “חיתוך” אם זה מפריע למישהו). הנה, תראו הוכחה על ידי תמונה:
אם כן, אנחנו יודעים שעבור \( l=\pi d \) (היקף מעגל שקוטרו \( d \), כמובן) מתקיים \( E\left[\pi d\right]=c\pi d=2 \), כלומר \( c=\frac{2}{\pi d} \) וסיימנו. לא יודע מה איתכם, אותי הטיעון הזה, עם המעגל שבא משום מקום, פשוט הפיל לקרקע מרוב שהוא אדיר.
מי שהמציא/גילה את ההוכחה הנפלאה הזו הוא המתמטיקאי הצרפתי Joseph-Émile Barbier. אבל הוא לא עצר כאן - למעשה, מה שעשינו כאן הוא הוכחה לתוצאה עוד יותר מעניינת, שמושגת כאשר הופכים את מה שעשינו כאן על פיו. לצורך כך, בואו נאמר שצורה קמורה היא בעלת רוחב קבוע \( d \) אם לכל שני קווים מקבילים שמשיקים לצורה, המרחק ביניהם הוא \( d \). מעגל הוא בבירור צורה כזו, עם רוחב ששווה לקוטר שלה, אבל יש עוד צורות, למשל “משולש רולו”:
כעת, בהוכחה של הנוסחה עבור המחט של בופון השתמשנו במעגל עם קוטר \( d \) כי זו צורה פשוטה ונחמדה, אבל כל צורה קמורה עם רוחב קבוע \( d \) הייתה עובדת באותה המידה. הרוחב הקבוע אומר שלא משנה איך נשליך אותה על המחברת שלנו (כלומר, איך “סובבנו” אותה), או ששני קווי גבול במחברת ישיקו לה, או שבדיוק קו גבול אחד יעבור דרכה - ומכיוון שהיא קמורה, המשמעות היא שהוא יחתוך אותה בדיוק בשתי נקודות (לצורות לא קמורות זה לא עובד).
אם כן, ניקח צורה קמורה כלשהי מרוחב קבוע \( d \) ועם היקף \( l \). תוחלת מספר החיתוכים כשמשליכים אותה על המחברת הוא מצד אחד 2 מהסיבה שפירטתי כרגע, ומצד שני על פי הנוסחה הוא \( \frac{2l}{\pi d} \). מסקנה: \( \frac{2l}{\pi d}=2 \), או \( l=\pi d \). כלומר, ההיקף של הצורה הוא תמיד \( \pi d \), בין אם היא מעגל ובין אם לאו. להציב \( d=1 \) נותן את התוצאה הזו בצורה אפילו יותר ברורה, למי שפספס אותי לרגע:
כל צורה קמורה בעלת רוחב קבוע 1 היא בעלת היקף \( \pi \).
לא רק מעגלים.
את יום פאי הבא נחגוג עם פאי בצורת משולש רולו?
נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: