התמרת פורייה - מה זה בכלל?

בפוסט הקודם התחלנו לדבר על טורי פורייה. הצגתי אותם בתור הצגה של פונקציות ממשיות מחזוריות כסכום של סינוסים וקוסינוסים, אבל הדבר הראשון שאני רוצה לעשות עכשיו הוא להכליל את זה טיפה. כל הקטע הזה עם הפרדה בין הסינוסים והקוסינוסים, כך שיש לנו שני סטים שונים של מקדמים, הוא קצת מעייף ומאולץ. אפשר להציג את הטורים בצורה קצת יותר כללית וקומפקטית אם עוברים לדבר על פונקציות מרוכבות \( f:\left[-\pi,\pi\right]\to\mathbb{C} \) ומרשים למקדמים של טורי הפורייה להיות מספרים מרוכבים. המשמעות של זה היא שאנחנו משנים את המרחב שאנחנו עובדים מעליו קצת - מרחיבים אותו - וזה דורש תיקון קטן במכפלה הפנימית שעליה הכל מתבסס. עד עכשיו היא הייתה \( \left\langle f,g\right\rangle =\frac{1}{\pi}\int_{-\pi}^{\pi}f\left(x\right)g\left(x\right)dx \); עכשיו, כשאני מתחיל לדבר על פונקציות שיכולות להחזיר ערכים מרוכבים, היא תהיה \( \left\langle f,g\right\rangle =\frac{1}{2\pi}\int_{-\pi}^{\pi}f\left(x\right)\overline{g\left(x\right)}dx \). הסיבה להצמדה של \( g \) היא סטנדרטית - לשמור את תכונת ההרמיטיות של המכפלה, שהסברתי למה היא נדרשת ולא סתם סימטריה בפוסט שלי על מכפלות פנימיות. את הסיבה לחלוקה ב-\( 2\pi \) נראה עוד מעט.

מה היתרון שבהכנסת מרוכבים לתמונה? שהוא מאפשר לנו לדבר על פונקציית האקספוננט המרוכבת. התכונה הבסיסית של הפונקציה הזו היא נוסחת אוילר:

\( e^{ix}=\cos x+i\sin x \)

שאומרת לנו "אקספוננט מרוכב הוא בעצם דרך לכתוב קוסינוס וסינוס ביחד". אפשר "לשחזר" את הסינוסים והקוסינוסים לבדם מתוך אקספוננטים:

\( \cos x=\frac{e^{ix}+e^{-ix}}{2} \)

\( \sin x=\frac{e^{ix}-e^{-ix}}{2i} \)

עכשיו, אם ניקח אקספוננט כזה ונכפול אותו במקדם שהוא מספר מרוכב כללי \( a+bi \), נקבל:

\( \left(a+bi\right)e^{ix}=\left(a\cos x-b\sin x\right)+i\left(a\sin x+b\cos x\right) \)

כלומר, אנחנו מקבלים רכיב ממשי שמכיל סינוסים וקוסינוסים עם מקדם כלשהו, ורכיב מדומה שמכילה סינוסים וקוסינוסים עם מקדם כלשהו; לכן זה לא כל כך מפתיע שאפשר "לקודד" טורי סינוסים וקוסינוסים, גם טורים ממשיים למהדרין, בעזרת אקספוננט מרוכב. עוד מעט נטפל שוב בטורים שכבר ראינו בפוסט הקודם ונראה איך מתארים אותם בשיטת ההצגה החדשה שלנו.

בפוסט הקודם הפונקציות שהשתמשנו בהן היו \( \cos nx \) ו-\( \sin nx \) לכל \( n \) טבעי; כשעוברים לדבר על מרוכבים, הפונקציות הרלוונטיות הן \( e^{inx} \) לכל \( n \) שלם, כלומר כולל שליליים. הדבר הראשון שצריך לעשות הוא לבדוק שהפונקציות הללו עדיין אורתונורמליות, אז בואו נעשה חישוב זריז:

\( \left\langle e^{inx},e^{ikx}\right\rangle =\frac{1}{2\pi}\int_{-\pi}^{\pi}e^{inx}\overline{e^{ikx}}dx=\frac{1}{2\pi}\int_{-\pi}^{\pi}e^{inx}e^{-ikx}dx=\frac{1}{2\pi}\int_{-\pi}^{\pi}e^{i\left(n-k\right)x}dx \)

עכשיו צריך להבדיל בין שני מקרים. אם \( n=k \) אז \( e^{i\left(n-k\right)x}=e^{i0x}=1 \) ולכן \( \frac{1}{2\pi}\int_{-\pi}^{\pi}e^{i\left(n-k\right)x}dx=\frac{1}{2\pi}\int_{-\pi}^{\pi}dx=1 \). אם כן, הסיבה ששינינו את \( \frac{1}{\pi} \) ל-\( \frac{1}{2\pi} \) הוא כדי להבטיח שכל הפונקציות שלנו יהיו מנורמה 1 תחת המכפלה הפנימית שלנו. שימו לב שעכשיו כבר אין מקרה קצה מוזר עם אחד המקדמים (זה שגרם לנו לכתוב \( \frac{a_{0}}{2} \) עבור טורים ממשיים).

במקרה שבו \( n\ne k \) צריך להמשיך לחשב את האינטגרל. אסמן \( t=n-k \) לצורך פשטות:

\( \frac{1}{2\pi}\int_{-\pi}^{\pi}e^{itx}dx=\frac{1}{2\pi}\left[\frac{e^{itx}}{it}\right]_{-\pi}^{\pi}=\frac{1}{\pi t}\frac{e^{it\pi}-e^{-it\pi}}{2i}=\frac{1}{\pi t}\sin t\pi=0 \)

אפשר היה לסיים את החישוב עוד קצת קודם, אבל רציתי שנראה איך פתאום החלק המרוכב נעלם כולו ואנחנו נשארים עם משהו ממשי (שמהר מאוד מתברר שהוא 0). אני רוצה עכשיו למצוא את הטור של פונקציה שכבר טיפלנו בה, אבל קודם בואו ננסח מחדש את מה שאני רוצה שנעשה בלשון המרוכבת החדשה: יש לי פונקציה \( f:\left[-\pi,\pi\right]\to\mathbb{C} \) שהיא אינטגרבילית בריבוע (\( \int_{-\pi}^{\pi}\left|f\right|^{2}<\infty \)). אנחנו רוצים לכתוב את \( f \) בצורה הבאה:

\( f\left(x\right)=\sum_{n=-\infty}^{\infty}a_{n}e^{inx} \) (ושוב האזהרה הקבועה שלי - זה לא שוויון נקודתי! סימן השוויון מציין התכנסות בנורמה, לא התכנסות נקודתית).

כך שאת המקדמים ניתן למצוא על ידי הנוסחה

\( a_{n}=\frac{1}{2\pi}\int_{-\pi}^{\pi}f\left(x\right)e^{-inx}dx \)

(המינוס בחזקה של האקספוננט הוא בגלל שאנחנו מצמידים אותו).

בפוסט הקודם דיברתי על הפונקציה \( f\left(x\right)=\begin{cases}-1 & -\pi\le x<0\\1 & 0\le x\le\pi\end{cases} \). מה קורה איתה בנוסחה החדשה? אני אניח שאתם יודעים תעלולים לחישוב אינטגרלים ולא אסביר כל צעד שאעשה:

\( a_{n}=-\frac{1}{2\pi}\int_{-\pi}^{0}e^{-inx}dx+\frac{1}{2\pi}\int_{0}^{\pi}e^{-inx}dx=\frac{1}{2\pi}\left[-\int_{0}^{\pi}e^{inx}dx+\int_{0}^{\pi}e^{-inx}dx\right]= \)

\( -\frac{i}{\pi}\int_{0}^{\pi}\frac{e^{inx}-e^{-inx}}{2i}dx=-\frac{i}{\pi}\int_{0}^{\pi}\sin nxdx=-\frac{i}{\pi}\left[-\frac{\cos nx}{n}\right]_{0}^{\pi} \)

כמו בפוסט הקודם, המקדמים הזוגיים מתאפסים ונותרים רק האי-זוגיים, ולכן הטור הוא:

\( f\left(x\right)=\sum_{n=-\infty}^{\infty}-\frac{2i}{n\pi}e^{inx} \)

כאשר אנו מסכימים על כך שהסכום הוא רק על הערכים האי-זוגיים של \( n \). הסכום הזה לא נראה הכי נחמד בעולם, אבל אפשר לפשט אותו בקלות: \( -\frac{2i}{n\pi}=\frac{4}{\pi}\cdot\frac{1}{2i}\frac{1}{n} \). כמו כן, לכל \( n>0 \) אי זוגי אפשר לחבר את האיבר השלילי המתאים לו ולקבל \( -\frac{2i}{n\pi}e^{inx}+\left(-\frac{2i}{-n\pi}e^{i-nx}\right)=-\frac{2i}{n\pi}\left(e^{inx}-e^{-inx}\right)=\frac{4}{\pi}\frac{e^{inx}-e^{-inx}}{2i}\frac{1}{n}=\frac{4}{\pi}\frac{\sin nx}{n} \)

כלומר, אותם מקדמים שקיבלנו גם בפוסט הקודם (בפוסט הקודם זה היה קצת יותר קל, אבל תזכרו שזו פונקציה פשוטה עם פיתוח ברור לטור סינוסים). אני מקווה שהדוגמה הזו מצליחה "להרגיע" את מי שבמבט ראשון היה מבועת (כמוני בשעתו) מכך שאנחנו מזהמים את הסינ וסים והקוסינוסים הממשיים הנחמדים שלנו עם מספרים מרוכבים - כפי שאפשר לראות, המרוכבים חכמים ויודעים מתי לצאת בנימוס מהבמה כשאין בהם צורך.

לסיום, קצת על טרמינולוגיה. להגיד כל הזמן "סינוסים וקוסינוסים", או "אקספוננטים" או "פונקציות טריגונומטריות" זה מעייף. מעכשיו אני אשתמש במילה הרמוניות כשאני בא לדבר על הפונקציות שמפרקים אליהן בפירוק לטור פורייה (כלומר הסינוסים והקוסינוסים, או האקספוננטים - תמיד אני אתכוון לאקספוננטים אלא אם אומר אחרת). אני לא אוהב את המילה הזו כל כך, אבל היא קצרה.

עכשיו אני רוצה לעבור לנושא חדש, אבל כמובן שקשור בקשר הדוק לטורי פורייה: התמרת פורייה. על רגל אחת ובתיאור פשטני, התמרת פורייה זה כמו טורי פורייה רק עבור פונקציות שמוגדרות על כל \( \mathbb{R} \) (כלומר, לא רק על קטע סגור), ועם מספר לא בן מניה של מקדמים. על פניו לא ברור מה זה אומר - מה זה טור עם מספר לא בן מניה של מקדמים? איך מתארים דבר כזה בכלל? אבל בפועל כולנו כנראה מכירים את זה: אינטגרל הוא דוגמה לטור שכזה. מה זה אינטגרל? כמו סכום (הצורה שלו, \( \int \), היא פשוט S מוארך, מהמילה "Sum" - או לפחות זה הצ'יזבט), כשהאיברים שסוכמים מתוארים על ידי פונקציה. כמובן שזה לא עד כדי כך פשוט - האינטואיציה שמאחורי אינטגרל היא שסוכמים מספר לא בן מניה של איברים אבל שלכל אחד מהם יש "משקל" אפסי ולכן הסכום יכול לצאת סופי גם אם כל האיברים חיוביים; אבל זו אינטואיציה לא רעה כדי להבין במה אינטגרל דומה לסכום.

אז אם בטורי פורייה התחלנו עם פונקציה \( f \) וניסינו למצוא סדרה \( \dots,a_{-2},a_{-1},a_{0},a_{1},a_{2},\dots \) של מקדמים שמתארת את הרכיבים שלה בפירוק להרמוניות, בהתמרת פורייה אנחנו מתחילים מפונקציה \( f \) ומנסים למצוא פונקציה \( \hat{f} \) שגם כן מתארת את הרכיבים של \( f \) בפירוק להרמוניות.

פורמלית אם \( f:\mathbb{R}\to\mathbb{C} \) אז נגדיר את התמרת פורייה שלה כך:

\( \hat{f}\left(\omega\right)=\int_{-\infty}^{\infty}f\left(t\right)e^{-2\pi i\omega t}dt \)

הנוסחה הזו אמורה להזכיר לנו את הנוסחה לחישוב המקדמים בטור פורייה, כשהפעם במקום לדבר על המקדם ה-\( n \)-י אנחנו מדברים על הערך של \( \hat{f} \) ב-\( \omega \). הנוסחה המקבילה להצגה של \( f \) בתור טור היא הצגה של \( f \) בנקודה כלשהי בתור אינטגרל על ההתמרה - נוסחה שנקראת "התמרת פורייה ההפוכה" (וצריך לנסח מתי הנוסחה עובדת ולהוכיח זאת ולא אעשה זאת כרגע כי זה לא טריוויאלי):

\( f\left(t\right)=\int_{-\infty}^{\infty}\hat{f}\left(\omega\right)e^{2\pi i\omega t}d\omega \)

שימו לב שעכשיו אין מינוס על האקספוננט - גם זה תואם את שתי הנוסחאות שראינו במקרה של טורים, שאכתוב כעת שוב כדי שיהיה קל להשוות:

\( a_{n}=\frac{1}{2\pi}\int_{-\pi}^{\pi}f\left(x\right)e^{-inx}dx \)

\( f\left(x\right)=\sum_{n=-\infty}^{\infty}a_{n}e^{inx} \)

הנוסחאות של ההתמרה נראות יפות ודומות יותר כי ההתמרה של \( f:\mathbb{R}\to\mathbb{C} \) גם היא פונקציה \( \hat{f}:\mathbb{R}\to\mathbb{C} \), אבל הרעיון הוא אותו רעיון בבסיסו.

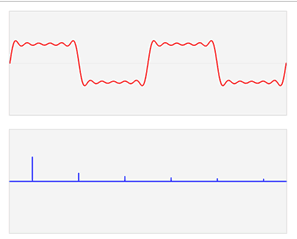
שימו לב לבחירה שלי לשמות המשתנים ש-\( f \) מקבלת וש-\( \hat{f} \) מקבלת. זו לא בחירה מקרית. בשני המקרים הייתי יכול לקרוא למשתנה \( x \) וגמרנו, אבל השימוש ב-\( t \) ו-\( \omega \) עוזר להבין מתי אנחנו מדברים על הפונקציה המקורית ומתי על ההתמרה וזה חשוב כשמתעסקים עם אפליקציות. בפרט, אפליקציה נפוצה היא ניתוח של אותות - למשל, גלי קול. אפשר לתאר גל קול (בצורה פשטנית, כמובן) בתור פונקציה שמתארת את העוצמה שלו כפונקציה של הזמן. זו הפונקציה \( f\left(t\right) \) - המשתנה \( t \) מייצג זמן. התמרת פורייה משנה את נקודת המבט שלנו: אנחנו מפרקים את \( f \) למעין סכום של המוני גלים של סינוסים וקוסינוסים - כל גל כזה מאופיין על ידי תדירות \( \omega \), והפונקציה שמתארת את העוצמה שלו כפונקציה של הזמן היא \( e^{2\pi i\omega t} \) (כאן \( t \) הוא המשתנה ואילו \( \omega \) הוא קבוע, כלומר סימון קצת יותר ברור לפונקציה הוא \( g_{\omega}\left(t\right)=\left(e^{2\pi i\omega}\right)^{t} \)). התמרת פורייה של \( f \) מחזירה לנו פונקציה שלכל תדירות \( \omega \) אומרת מה העוצמה של הרכיב בעל תדירות \( \omega \) בתוך \( f \). כלומר - אנחנו מפרקים את \( f \) לגלים בתדירויות שונות שמרכיבים אותו ומסתכלים על העוצמה של כל תדירות כזו בנפרד. אוהבים להגיד שהתמרת פורייה מעבירה אותנו "ממרחב הזמן" אל "מרחב התדר". לצורך הדוגמה הנה תמונה של פונקציית גל שכזו, וההתמרה שלה:

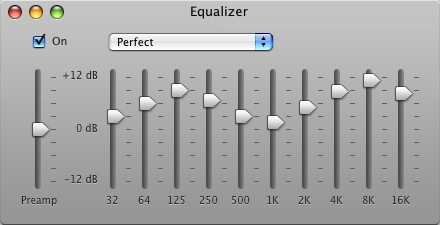
אינטואיצה טובה לסיפור הזה אפשר לשאוב ממשהו שאני מקווה שרובכם מכירים - אקוולייזר:

אקווליזר לוקח גל קול, ומאפשר לנו לשנות אותו על ידי ביצוע הגברות והחלשות של תדירויות מסויימות. במוזיקה זה מאוד אפקטיבי - כלים שונים מייצרים צלילים בתדירויות שונות, ולכן אקוולייזר מאפשר להבליט או להחליש כלים מסויימים. דרך הפעולה של אקוולייזר היא לא טריוויאלית, אבל אינטואיטיבית אפשר לחשוב על לקחת את הפונקצייה של הצליל שלנו, לבצע לה התמרת פורייה, לשנות נקודתית חלק מהערכים בפונקציה המותמרת שקיבלנו, ואז להתמיר בחזרה (ואיך עושים את זה בפועל? זה כבר עניין לפוסט נפרד שייכתב על ידי מישהו שמבין את הנושא).

כמובן, הרעיון הזה של פירוק למרכיבים בתדירויות שונ ות אינו בלעדי לגלי קול ואפשר למצוא אותו בשלל מקומות - דוגמה מתבקשת מאוד היא תחום הספקטרוגרפיה, שמאפשר ניתוח של המוני דברים - החל מאטומים וכלה בכוכבים רחוקים - לפי ספקטרום הקרינה האלקטרומגנטית שהם פולטים (אילו תדרים כלולים בקרינה הזו - חומרים שונים פולטים קרינה בתדרים שונים, ולכן הספקטרום מהווה מעין "חתימה" של החומר).

לי אישית נראה מאוד מוזר בהתחלה שבתוך \( f \) "מתחבא" כל המידע הזה על התדרים - מאיפה זה מגיע? איך אפשר לדעת מה הערך של תדר מסויים, אם כל מה שיש לנו זה את העוצמה של \( f \) לאורך זמן? ובכן, העניין הוא בכך שלכל תדר אנחנו יודעים בדיוק איך יתנהג הגל שזה התדר שלו - מתי הגל יהיה חזק, ומתי יהיה חלש. אנחנו גם יודעים שהערך של \( f \) בכל נקודת זמן נקבע על ידי התאבכות - התופעה שבה גלים שונים "מתערבבים" ויוצרים גל חדש, שהעוצמה שלו תלויה לא רק בעוצמה האבסולוטית של הגלים אלא גם במצב שלהם ברגע הערבוב שאנחנו מסתכלים עליו (קשה להסביר על גלים על רגל אחת, אבל יש לזכור שגל הוא לא משהו שקבוע בעוצמה מסויימת - אפשר לחשוב עליו כאילו הוא משתנה באופן תמידי בין העוצמה המקסימלית שלו ובין מינוס העוצמה המקסימלית שלו, כמו שסינוס מקפץ לו בין 1 ובין מינוס 1). אם כן, כל יחידת זמן מלמדת אותנו משהו על איך נראית הערבוביה של כל הגלים שמרכיבים את \( f \) ברגע נתון, ומכיוון שיש לנו את המידע על \( f \) בכל הרגעים האפשריים אנחנו מצליחים לשחזר את עוצמת התדירויות שמרכיבות את \( f \).

וכעת זה הזמן לקומיקס האלמותי של xkcd שמזהיר מפני ביצוע לא זהיר של התמרות פורייה:

התיאוריה סביב התמרת פורייה היא מסובכת למדי ובוודאי לא משהו שאוכל להציג בפוסט המבוא. אני רק רוצה להסתפק בינתיים בהצגה של בעיה אחת והסבר מחופף לגבי איך פותרים אותה. הנה בעיה - איך נראית ההתמרה של גל שמורכב מהרמוניה בודדת? נאמר, מה ההתמרה של \( f\left(t\right)=e^{2\pi it} \) (כאן \( \omega=1 \))? ובכן, נפעיל את נוסחת ההתמרה ונקבל:

\( \hat{f}\left(\omega\right)=\int_{-\infty}^{\infty}f\left(t\right)e^{-2\pi i\omega t}dt=\int_{-\infty}^{\infty}e^{2\pi it}e^{-2\pi i\omega t}dt=\int_{-\infty}^{\infty}e^{2\pi it\left(1-\omega\right)}dt \)

אם \( \omega\ne1 \) אנחנו מקבלים פונקציה מחזורית ולא ברור אם האינטגרל מתכנס בכלל, אבל אפשר לפרק אותו לסכום של אינסוף קטעים שעל כל אחד מהם האינטגרל הוא 0, אז נניח. אבל אם \( \omega=1 \) אנחנו מקבלים את האינטגרל \( \int_{-\infty}^{\infty}dt \) שבכלל לא מתכנס. מה הולך כאן? משהו בבירור לא עובד עם ההגדרות הרגילות שלנו. זה לא כל כך מפתיע למי שכבר נתקל בסיבוכים הללו במקומות אחרים, נאמר בתורת ההסתברות; כאשר מרחב ההסתברות שלנו אינו בן-מניה, למשל הוא \( \mathbb{R} \), אז נובע שההסתברות של אירוע ספציפי (נאמר, \( a\in\mathbb{R} \)) חייבת להיות 0. אפשר לייחס הסתברות חיובית רק לתת-קבוצה של אירועים ספציפיים שהיא "גדולה מספיק", וזה נראה אבסורדי במבט ראשון כי תוצאת ההגרלה שלנו תהיה איבר ספציפי במרחב - שההסתברות שלו היא לכאורה 0. באופן דומה, גם התורה שהצגתי עד כה של התמרת פורייה לא יודעת "לאכול" גלים שמורכבים ממספר קטן מדי של תדירויות שכל אחת מהן לכשעצמה היא חזקה. זה לא שאי אפשר לתאר דברים כאלו; זה שהפורמליזם המתמטי הנוכחי שלנו לא מתאים לתיאור שלהם.

ההרחבה של הפורמליזם שלנו נעשית באמצעות מה שנקרא פונקציית הדלתא של דיראק. אינטואיטיבית, זו פונקציה \( \delta\left(\omega\right) \) כך ש-\( \delta\left(\omega\right)=0 \) אם \( \omega\ne0 \), וכמו כן מתקיים \( \int_{-\infty}^{\infty}\delta\left(\omega\right)d\omega=1 \). ברור שאם אני רוצה להגדיר את \( \delta \) בתור פונקציה "רגילה" זה לא יעבוד. פונקציה רגילה שהיא אפס בכל מקום חוץ מבנקודה אחת, האינטגרל שלה יהיה אפס. אם רוצים לטפל בכל זה פורמלית צריך להכליל את ההגדרות של פונקציות ואינטגרלים (אל נא תתפתו לחשוב שזה מה שפורייה וחבריו בני זמנו עשו בפועל! הפורמליזם הגיע הרבה אחר כך). יש שתי דרכים פורמליות מקובלות להגדיר את הדלתא של דיראק ופונקציות דומות - אחת היא לראות אותן בתור מידות (Measure) והשניה היא לראות אותן בתור התפלגויות (Distribution). כל אחת מדרכי ההתבוננות ראויה לפוסט נפרד וכרגע לא אגיד עליהן כלום חוץ מלנסות להרגיע אתכם - יש פורמליזם. הוא עובד. כולם שמחים. המתמטיקה ניצלה שוב.

אני רוצה לסיים בנסיון לקשר את שני המושגים שראינו עד כה - זה של התמרת פורייה, וזה של טורי פורייה. בשני המקרים אנחנו מתחילים עם פונקציה: במקרה של התמרה אסמן אותה בתור \( f:\mathbb{R}\to\mathbb{C} \), ובמקרה של טורים אסמן אותה \( g:\left[-\pi,\pi\right]\to\mathbb{C} \). מהפונקציה שאנחנו מתחילים ממנה אנחנו מקבלים פונקציה חדשה אשר מתארת, אינטואיטיבית, את המקדמים של הפונקציה בפירוק שלה לרכיבים הרמוניים. במקרה של התמרה זוהי פונקציה \( \hat{f}:\mathbb{R}\to\mathbb{C} \) ובמקרה של טורים זוהי פונקציה \( \hat{g}:\mathbb{Z}\to\mathbb{C} \) (סדרה שאבריה מאונדקסים על ידי מספרים שלמים היא, פורמלית, פשוט פונקציה מהשלמים). בנוסף, אפשר "לשחזר" את \( f,g \) מתוך \( \hat{f},\hat{g} \) תחת תנאים מסויימים על הפונקציה המקורית. למעבר מפונקציה להתמרה/טור שלה אקרא אנליזה (המשמעות המילולית של אנליזה היא פירוק שלם לחלקים) ול"שחזור" שלה אקרא סינתזה. אז גם התמרות פורייה וגם טור פורייה מתוארים על ידי משוואות אנליזה וסינתזה:

אנליזה:

\( \hat{f}\left(\omega\right)=\int_{-\infty}^{\infty}f\left(t\right)e^{-2\pi i\omega t}dt \)

\( \hat{g}\left(n\right)=\frac{1}{2\pi}\int_{-\pi}^{\pi}g\left(x\right)e^{-inx}dx \)

סינתזה:

\( f\left(t\right)=\int_{-\infty}^{\infty}\hat{f}\left(\omega\right)e^{2\pi i\omega t}d\omega \)

\( g\left(t\right)=\sum_{n=-\infty}^{\infty}\hat{g}\left(n\right)e^{inx} \)

אפשר לתאר את המעברים הללו על ידי דיאגרמה:

\( \begin{array}{ccc}f & \leftrightarrow & \hat{f}\\\\g & \leftrightarrow & \hat{g}\end{array} \)

עכשיו, אחרי שציירתי את זה, צץ מאליו (עבורי) הפיתוי לשאול אם אפשר להשלים את הדיאגרמה הזו עם עוד קצת חצים ולקבל דיאגרמה קומוטטיבית. מבלי להיכנס כעת לפורמליזם של מה זו דיאגרמה קומוטטיבית (מושג שמככב בעיקר באלגברה בכלל), הרעיון הוא כזה - האם אני יכול להוסיף עוד טרנספורמציות, אחת שמעבירה את \( f \) לפונקציה \( g \) מתאימה, ואחת שמעתיקה את \( \hat{f} \) לפונקציה \( \hat{g} \) מתאימה, כך שלא משנה אם אנחנו הולכים במסלול \( f\to\hat{f}\to\hat{g} \) או במסלול \( f\to g\to\hat{g} \), אם התחלנו מאותה \( f \) נגיע בסוף לאותה \( \hat{g} \) (ובדומה, אם התחלנו מאותה \( \hat{f} \) נגיע לאותה \( g \))? זה מצויר כך:

\( \begin{array}{ccc}f & \leftrightarrow & \hat{f}\\\downarrow & & \downarrow\\g & \leftrightarrow & \hat{g}\end{array} \)

לא מפתיע כל כך שיש טרנספורמציות כאלו. כבר ראינו שפונקציה וההתמרה/טור שלה קשורים בקשר הדוק - מתבקש שמניפולציה "במישור הזמן" תהיה בעלת מניפולציה שקולה "במישור התדר". עדיין, מה הן?

ובכן, אנחנו צריכים להגדיר כאן שני סוגים של טרנספורמציות. מה שמעביר את \( f \) ל-\( g \) היא טרנספורמציה שלוקחת פונקציה ממשית כללית והופכת אותה לפונקציה מחזורית על תחום מצומצמם. בגלל האופן שבו הטרנספורמציה הזו תתבצע אקרא לה טרנספורמציית סכימה. מה שמעביר את \( \hat{f} \) ל-\( \hat{g} \) לוקח פונקציה ממשית כללית ומעביר אותה לפונקציה שמוגדרת על השלמים - כלומר, על מרחב בדיד (אינטואיטיבית, מרחב "רציף" הוא מרחב שבו אין חורים ומרחב "בדיד" הוא מרחב שכולו מלא בחורים - אבל זה מאוד טריקי, כי למשל האינטואיציה הראשונית שלנו היא שהרציונליים הם רציפים, לא בדידים; לכן לא אכנס להסבר פורמלי מה זה מרחב בדיד). לטרנספורמציה שתעשה את זה אקרא טרנספורמציית דגימה. אם כן, זה מה שעלינו לתאר - סכימה ודגימה.

הרעיון בסכימה הוא זה: אנחנו רוצים לקבל פונקציה מחזורית \( g \) שמוגדרת ב-\( \left[-\pi,\pi\right] \) מפונקציה \( f \) שמוגדרת לכל \( \mathbb{R} \). אז במובן מסויים, הערך בנקודה \( a \) צריך להיות בנוי על הערכים של \( f\left(a\right) \) אבל גם \( f\left(a+2\pi\right) \) וגם \( f\left(a-2\pi\right) \) ובאופן כללי, \( f\left(a+2\pi n\right) \) לכל \( n\in\mathbb{Z} \). את כל הערכים הללו אנחנו צריכים לערבב בצורה שבה אם נחליף, למשל, את \( a \) ב-\( a+2\pi \), ההבדל הזה "ייבלע" בתוך ההגדרה. הדרך הפשוטה ביותר לעשות זאת היא פשוט לסכום את כל הערכים הללו, כלומר נגדיר \( g\left(a\right)=\sum_{n=-\infty}^{\infty}f\left(a+2\pi n\right) \). כמובן, נדרש שהטור הזה ייתכנס, אז אין משמעות לפעולת הסכימה עבור פונקציות שהטור אינו מתכנס עבורן. בהינתן ההגדרה הזו, טריוויאלי לראות ש-\( g \) שהתקבלה אכן מחזורית.

כמובן, ה-\( 2\pi \) שמופיע בהגדרה הוא שרירותי; אפשר באופן כללי לדבר על טרנספורמציית \( d \)-סכימה, לכל מספר \( d \), שמוגדרת בתור \( g\left(a\right)=\sum_{n=-\infty}^{\infty}f\left(a+dn\right) \). אצלנו פשוט \( d=2\pi \) וזה הפרמטר הרלוונטי של הפעולה.

פעולת הדגימה, באופן לא מפתיע, פשוט דוגמת פונקציה במקומות נבחרים. אני מעדיף לא להשתמש בכובעים יותר מדי, אז נשתמש באותיות גדולות: נניח ש-\( F:\mathbb{R}\to\mathbb{R} \) היא פונקציה, אז נבנה פונקציה חדשה \( G:\mathbb{Z}\to\mathbb{R} \) באופן הבא: \( G\left(n\right)=F\left(n\right) \).

רגע, מה עשינו כאן? זה לא קצת פשטני מדי? דגמנו את \( F \) רק במקומות שהם מספרים שלמים, אבל מה אם \( F \) "משתגעת" בין כל זוג ערכים כזה? לא עדיף שיהיה איזה פרמטר ששולט על גודל הפער בין נקודת דגימה אחת לבאה אחריה? אז בסדר, בואו נוסיף פרמטר \( h>0 \) למשחק ונקבע \( G\left(n\right)=F\left(hn\right) \).

עכשיו בואו נחזור לדיאגרמה הקומוטטיבית. נתחיל מפונקציה \( f:\mathbb{R}\to\mathbb{R} \). ראשית נפעיל עליה סכימה עם פרמטר \( d=2\pi \) ונקבל פונקציה \( g:\left[-\pi,\pi\right]\to\mathbb{R} \) שמוגדרת על ידי \( g\left(a\right)=\sum_{n=-\infty}^{\infty}f\left(a+2\pi n\right) \). כעת על הפונקציה הזו אפשר לחשב את טור פורייה המתאים: \( \hat{g}:\mathbb{Z}\to\mathbb{R} \) המוגדר על ידי \( \hat{g}\left(n\right)=\frac{1}{2\pi}\int_{-\pi}^{\pi}\left(\sum_{k=-\infty}^{\infty}f\left(x+2\pi k\right)\right)e^{-inx}dx \).

אז זו דרך אחת להגיע אל \( \hat{g} \). בואו נלך עכשיו בדרך השניה. אנחנו מתחילים מלחשב את התמרת פורייה של \( f \): \( \hat{f}\left(\omega\right)=\int_{-\infty}^{\infty}f\left(t\right)e^{-2\pi i\omega t}dt \). עכשיו ניקח את ההתמרה הזו, ונבצע בה דגימה. לתוצאה אקרא \( G \) בינתיים:

\( G\left(n\right)=F\left(hn\right)=\int_{-\infty}^{\infty}f\left(t\right)e^{-2\pi ihnt}dt \)

טוב, זה פשוט מזעזע. אנחנו מצפים ש-\( G \) תהיה שווה ל-\( \hat{g} \) אבל הן לא נראות דומות בכלל כרגע. אז מה נעשה? בתור התחלה, אולי כדאי לחשוב איזה ערך של \( h \) מתאים לנו כאן: אינטואיטיבית, אנחנו רוצים ש-\( e^{-2\pi ihnt} \) יהפוך להיות משהו דמוי \( e^{-inx} \). לשם כך אנחנו רוצים להיפטר מה-\( 2\pi h \) שיש בביטוי הראשון. כלומר, היינו רוצים שיתקיים \( 2\pi h=1 \), או במילים אחרות - מתבקש לבחור \( h=\frac{1}{2\pi} \).

יפה. מה קיבלנו? \( G\left(n\right)=\int_{-\infty}^{\infty}f\left(t\right)e^{-int}dt \). זה עדיין בעייתי, כי מאיפה יגיע ה-\( \frac{1}{2\pi} \) בחוץ? ובכן, זה מעיד על צורך לשנות קצת את פעולת הדגימה שלנו - לא מספיק לבצע רק דגימה, צריך אחר כך גם לבצע כוונון מחדש של הסקלה שלנו - לכפול את כל הפונקציה ב-\( \frac{1}{2\pi} \). אז אם לתאר באופן כללי: אנחנו מבצעים שילוב של פעולות דגימה וכוונון, שמגדירות פונקציה \( G\left(n\right)=hF\left(hn\right) \). במקרה שלנו, \( h=\frac{1}{2\pi} \), ואנחנו מקבלים:

\( G\left(n\right)=\frac{1}{2\pi}\int_{-\infty}^{\infty}f\left(t\right)e^{-int}dt \)

והיעד שלנו הוא:

\( \hat{g}\left(n\right)=\frac{1}{2\pi}\int_{-\pi}^{\pi}\left(\sum_{k=-\infty}^{\infty}f\left(x+2\pi k\right)\right)e^{-inx}dx \)

שתי הנוסחאות הללו הן כבר די בבירור אותו דבר. כדי לראות את זה פורמלית, נשים לב שאפשר להחליף את הסדר בין האינטגרל ובין הסכום (דורש, כמובן, הצדקה פורמלית) ולקבל

\( \hat{g}\left(n\right)=\frac{1}{2\pi}\sum_{k=-\infty}^{\infty}\int_{-\pi}^{\pi}f\left(x+2\pi k\right)e^{-inx}dx \)

עכשיו, לכל \( k \) אפשר לבצע החלפת משתנים: \( t=x+2\pi k \). האפקט של החלפת המשתנה הזה על גבולות האינטגרציה הוא פשוט: כאשר \( x=-\pi \) אז \( t=\pi\left(2k-1\right) \), וכאשר \( x=\pi \) אז \( t=\pi\left(2k+1\right) \), ולכן נקבל:

\( \hat{g}\left(n\right)=\frac{1}{2\pi}\sum_{k=-\infty}^{\infty}\int_{\pi\left(2k-1\right)}^{\pi\left(2k+1\right)}f\left(t\right)e^{-int}dt=\frac{1}{2\pi}\int_{-\infty}^{\infty}f\left(t\right)e^{-int}dt=G\left(n\right) \)

קסם! קיבלנו את הדיאגרמה הקומוטטיבית שלנו!

בפוסט הבא אציג סוג נוסף של טורי והתמרת פורייה - כאלו שמבוצעים על מרחבים שהם בדידים מראש. ואז הריבוע הקומוטטיבי שלנו יהפוך להיות קוביה קומוטטיבית. יהיה כיף.