בניות בסרגל ומחוגה - המשחק!

בתור סטודנט למתמטיקה, נתקלתי לראשונה במושג של בניות בסרגל ומחוגה בקורס בתורת השדות. מה שעושים שם הוא להוכיח תוצאה שכיום היא כבר קלאסית לגמרי - ששלוש בעיות בניה מפורסמות אינן פתירות כלל. יש לי פוסט על התוצאה הנפלאה הזו, אבל זה לא מה שאני רוצה לדבר עליו עכשיו, אלא על מה שאנחנו “מפספסים” בכך שאנחנו מתמקדים בתוצאה הזו - אנחנו שוכחים מה כן אפשר לעשות עם בניות בסרגל ומחוגה. בפרט, אנחנו לא “מרגישים” מה זה בכלל אומר לבצע בניות בסרגל ומחוגה, ומה אפשר לעשות עם זה, כי אנחנו ממהרים לתרגם את הבעיה לבעיה אלגברית ולשכוח מהמשחק המקורי.

אמת, ה”תרגום” הזה כולל ביצוע של כמה בניות ספציפיות, אבל אנחנו עדיין מפספסים שלל בניות פשוטות יותר, בניות נוספת שמאפשרות לנו להרגיש שאפשר לעשות הרבה דברים מעניינים שמתקשרים לגאומטריה האוקלידית שאנחנו מכירים, ואנחנו לא ממש מתנסים עצמאית. ובכן, כל אחד שמצוייד בסרגל ומחוגה יכול להשתעשע איתם עצמאית, אבל בואו נודה בזה - זה לא הכי נוח ואנחנו מאוד מפונקים בימינו. אז יש תוכנה נהדרת בשם GeoGebra שמאפשרת לשחק עם בניות בסרגל ומחוגה (ועוד דברים) עצמאית, אבל אנחנו מפונקים מדי אפילו מכדי להוריד תוכנה ולשחק איתה באופן חופשי. אנחנו רוצים משימות. וקיצורי דרך. ושהכל ירוץ בתוך הדפדפן. ועכשיו מישהו (לצערי, לא אני) בא ועשה את זה.

המשחק נקרא Euclid the game ואפשר למצוא אותו כאן. הוא מבוסס על GeoGebra אבל הוא רץ בדפדפן, והוא מבוסס משימות, ויש בו קיצורי דרך (אחרי ביצוע חלק מהמשימות, הן מתווספות בתור כלי חדש שאפשר להשתמש בו). המטרה הראשונה של הפוסט היא להפציר בכם - לכו, רוצו, אוצו ושחקו במשחק הזה. אל תקראו עוד שום דבר. אפילו אם אתם לא יודעים בכלל מה זה בניות בסרגל ומחוגה. ככל שתדעו פחות, יותר טוב. יש לכם כאן הזדמנות להרגיש את אחד מהאספקטים של חדוות המתמטיקה - מיני “מחקר” ובניה של דברים יש מאין. אתם מסוגלים לעשות את זה עצמאית. אני מאמין בכם. רוצו.

נשארתם? שיחקתם קצת וחזרתם? אוקיי. אני לא רוצה לסיים את הפוסט כאן אלא תחת זאת להציג את הפתרונות שלי ל-20 השלבים שכרגע קיימים במשחק. זאת מכמה סיבות. ראשית, ייתכן שהמשחק ייעלם מחר מהרשת, אז לפחות שמשהו יישאר. שנית, כי זה מעניין ובטח יהיה ביקוש לפתרונות. הפתרונות שלי הם לא בהכרח אופטימליים או “הכי נכונים” בשום צורה; אני בטוח שבתגובות יציגו פתרונות יותר טובים לחלק מהדברים שאעשה. כרגיל, אנסה להציג את הרעיון שמאחורי הפתרון ואיך אני עצמי הקטן (שממש לא חזק בגאומטריה או בבניות בסרגל ומחוגה) הגעתי אליו.

לפני שניגש לאקשן, בכל זאת, הסבר קטן מה זה בכלל אומר, “בניות בסרגל ומחוגה”. הקונספט מגיע מתקופת יוון העתיקה; היוונים מאוד אהבו גאומטריה של המישור, ושניים מן הכלים ששימשו אותם בביצוע בניות גאומטריות היו, במפתיע, סרגל ומחוגה. ראשית כל חשוב להבהיר שסרגל כאן הוא לא בדיוק מה שאנחנו מכירים - בסרגלים שבהם אנחנו משתמשים יש שנתות שמאפשרות למדוד אורכים. בסרגל שאנחנו מדברים עליו כאן אין שנתות כאלו; כל מה שהסרגל מאפשר לנו לעשות הוא לצייר קווים ישרים, לרוב דרך שתי נקודות נתונות. באנגלית יש הבדל בין Ruler (שמודד אורכים) ובין Straightedge (שעליו אנחנו מדברים כאן) אבל בעברית אין הבדל כזה. שנית, מחוגה היא כלי שמאפשר לשרטט מעגלים: יש לה שתי רגליים, אחת מחודדת והשניה עם ראש של עפרון. מניחים את הרגל המחודדת בנקודה שרוצים שתהיה מרכז המעגל ואת הרגל השניה על נקודה כלשהי שרוצים שתהיה על המעגל, ומסובבים. אפשר להרחיב את הפער בין הרגליים כדי ליצור מעגלים עם רדיוסים גדולים יותר. בפועל לא נשבור את הראש על הכלים הפיזיים - במשחק, היכולות שלנו כוללות “להעביר קטע בין שתי נקודות” (או להעביר קרן - קטע שנמשך עד אינסוף בכיוון כלשהו) ו”לצייר מעגל עם מרכז נתון ונקודה נתונה שעליו” ו”ליצור נקודה חדשה בחיתוך של אובייקטים קיימים”. והשאלה היא מה אפשר לעשות, גאומטרית, עם הכלים הללו. מסתבר שאפשר לעשות הרבה. הבה ונעבור לתרגילים.

שלב 1 - בניית משולש שווה צלעות

כאן נתון לנו קטע כלשהו, ואנחנו רוצים לבנות משולש שווה צלעות שהקטע הזה הוא אחת מצלעותיו. כלומר, אנחנו רוצים למצוא נקודה C שמרחקה מהנקודות A,B זהה למרחק שבין A,B (זה ממש שקול לאמירה שאנחנו רוצים לבנות משולש שווה צלעות). הרעיון הוא כזה: הבה ונסתכל על כל הנקודות שמרחקן מ-A שווה למרחק של A מ-B. אוסף הנקודות הזה הוא בדיוק המעגל שמרכזו ב-A וכולל את B. לכן אני מצייר את המעגל הזה. ואני עושה דבר דומה עבור B. כעת, הנקודות בחיתוך של שני המעגלים הן בדיוק הנקודות שמקיימות בו זמנית את שני התנאים “המרחק של הנקודה מ-A שווה לאורך AB” ו”המרחק של הנקודה מ-B שוה לאורך AB” ולכן כל אחת משתי נקודות החיתוך מתאימה למשולש שאנחנו רוצים לבנות. אז אני מצייר אותה, מחבר אותה בקטעים ל-A,B, וסיימנו.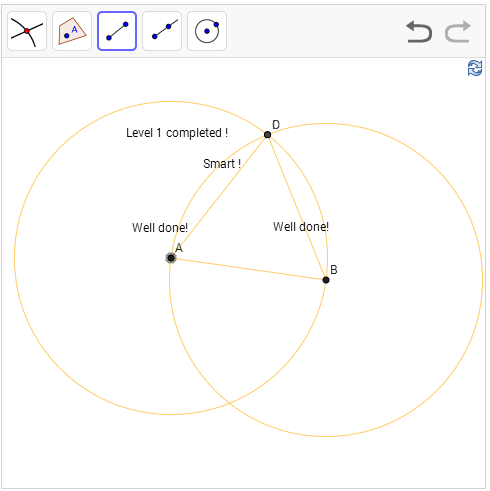

שלב 2 - חלוקת קטע לשניים

כאן נתון לנו קטע AB ואנחנו רוצים לחלק אותו לשני חלקים שווים. אם לחשוב על זה אלגברית, אנחנו רוצים להראות כאן שאנחנו יודעים “לחלק ב-2”. איך ניגשים לזה? ובכן, למה שלא נשתמש במה שכבר למדנו איך לבנות - נבנה את שני המשולשים שווי הצלעות ש-AB היא צלע שלהם (למי שלא מצליחים לעשות זאת במשחק - פעם אחת בחרו את A ואז את B, ובפעם השניה בחרו את B ואז את A). הצורה שנקבל היא מעוין (מרובע שאורך כל צלעותיו שווה; במקרה שלנו, שווה ל-AB), כאשר הצלע AB היא אלכסון של המעוין. מעוין הוא מקרה פרטי של מקבילית, ולכל מקבילית יש את התכונה שהאלכסונים שלה חוצים זה את זה. לכן כל שנותר לי לעשות הוא להעביר את האלכסון השני ולסמן את נקודת החיתוך שלו עם AB, והנה הצלחתי לחלק את AB לשניים.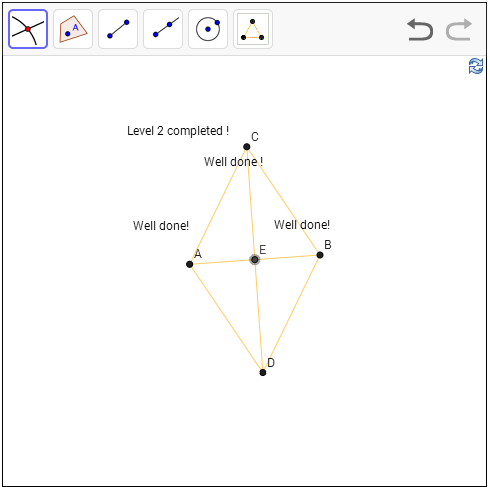

שלב 3 - חלוקת זווית לשניים

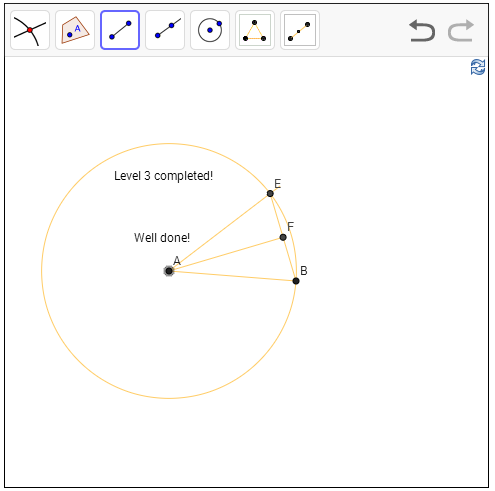
מהי זווית? קחו שני קטעים שנפגשים בנקודה משותפת; הזווית ביניהם היא “כמות הסיבוב” שנדרשת כדי שנסובב את אחד הקטעים עד שיעלה על השני. זו הגדרה קצת מוזרה כי ברור שיש לפחות שתי זווית בין כל זוג קטעים, אבל אני מניח שאתם מבינים את הכוונה. לחלק זווית לשתיים פירושו לקחת שני קטעים עם נקודה משותפת ולבנות בינם קטע שלישי, כך שהזווית שהוא יוצר עם כל אחד מהקטעים היא שווה. איך נעשה את זה? ובכן, משפט בסיסי על זוויות נוגע למשולשים שווי שוקיים: במשולש כזה, התיכון לבסיס (קטע שמחלק את הבסיס לשני חלקים שווים) הוא גם חוצה זווית. אנחנו כבר יודעים לבנות חוצה של קטע, אז ההמשך די ברור - אנחנו רוצים לבנות משולש שווה שוקיים מתאים ולבנות את התיכון בו. האתגר כאן הוא בכלל שונה - איך נבנה את המשולש שווה השוקיים הזה? נתונה לנו הנקודה A שבה שני הקטעים נפגשים, ועוד נקודה B על אחד מהקטעים - מה שאנחנו רוצים לעשות הוא למצוא נקודה C על הקטע השני שמרחקה מ-A שווה ל-AB. כבר ראינו איך להשתמש במעגלים בשביל זה, ומכאן הפתרון בא מאליו. אגב, נקודה מעניינת היא שחלוקת זווית לשלושה חלקים היא בלתי אפשרית לביצוע בעזרת סרגל ומחוגה - זו אחת מהבעיות שהזכרתי בתחילת הפוסט, ועכשיו אנחנו רואים איך היא צצה באופן טבעי.

שלב 4 - לבנות אנך לקטע העובר דרך נקודה נתונה על הקטע

אנך לקטע הוא קטע אחר, אשר הזווית בינו לבין הקטע המקורי היא ישרה (בת 90 מעלות, כלומר רבע של סיבוב שלם). כדי לפתור את זה, אני שולף עוד תוצאה על משולשים שווי שוקיים: לא רק שהתיכון בהם הוא חוצה זווית, הוא גם אנך לבסיס. אז כל מה שאני צריך לעשות הוא לבנות משולש שווה שוקיים שהבסיס שלו הוא הקטע הנתון, והנקודה A הנתונה היא בדיוק במרכז הבסיס של המשולש. זה אומר שאני צריך להתחיל עם שתי נקודות על הקטע ש-A נמצא בדיוק באמצע הדרך ביניהן; כלומר, שהמרחק שלו משתיהן שווה; כלומר, נבנה מעגל ש-A במרכזו ועם רדיוס שרירותי לגמרי, ונחתוך אותו עם הקטע שלנו. נקבל את שתי נקודות הבסיס של המשולש שווה השוקיים שלנו, ואז נבנה עליהן משולש שווה צלעות (שהוא בפרט שווה שוקיים). נחבר את הקודקוד הנוסף שלו עם A, וסיימנו!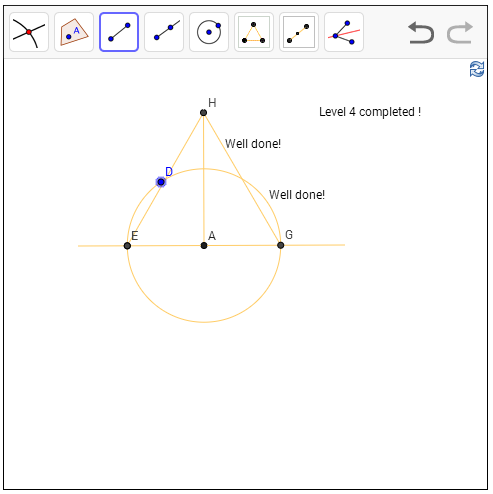

שלב 5 - לבנות אנך לקטע העובר דרך נקודה נתונה מחוץ לקטע

מה שעשיתי בשלב 4 היה לבנות משולש שווה שוקיים שקודקודו העליון יכול להיות לא-משנה-איפה. עכשיו מגבילים אותי - רוצים שהאנך שלי יעבור דרך נקודה מסויימת מחוץ לקטע. איך עוקפים את המגבלה הזו? האינסטינקט הראשון שלי היה לקחת את A  - אחת הנקודות על הקטע - ואת C - הנקודה מחוץ לקטע - ולבנות עליהן משולש שווה צלעות. משום מה חשבתי שהנקודה הנוספת שלו תהיה על הקטע. אבל זה לא נכון, כפי שקצת משחק עם הנקודות הקיימות והזזה שלהן מראה. זו דוגמה קלאסית של “הוכחה על ידי ציור” שגויה. אז לא, הרעיון הזה טיפשי ולא מוביל לשום מקום. אז מה כן? ובכן, שום דבר מחוכם. באמת צריך לבנות משולש שווה שוקיים שהקודקוד העליון שלו הוא C ואחד מקודקודי הבסיס הוא A, רק צריך להבין איך למצוא את נקודת הקצה השניה. היא צריכה להיות על הקטע שאנחנו בונים לו אנך; והיא צריכה להיות במרחק מ-C שהוא בדיוק AC. אז נשתמש במעגל, כרגיל: נבנה מעגל שמרכזו ב-C ורדיוסו AC ונחתוך אותו עם הקטע. עכשיו אפילו אין צורך לצייר במפורש את המשולש; אני רק מוצא את נקודת האמצע בין A ונקודת החתוך E, ומחבר אותה בקטע אל C.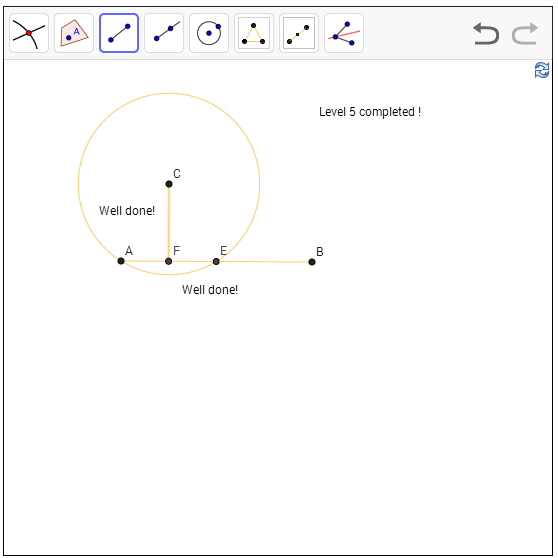

שלב 6 - לבנות מקביל לקטע נתון העובר דרך נקודה מחוץ לקטע

התרגיל הזה מזכיר לנו את אקסיומת המקבילים, שאומרת שבהינתן קטע נתון ונקודה מחוץ לקטע, קיים (בגאומטריה אוקלידית!) ישר יחיד העובר דרך הנקודה הזו ומקביל לקטע. אבל כאן המטרה שלנו היא לבנות אותו, לא להוכיח שהוא קיים. והפתרון פשוט להחריד - אנחנו יודעים שכל זוג צלעות שלא נוגעות אחת בשניה במלבן (מרובע שכל הזוויות בו הן 90 מעלות) הן מקבילות; אז בואו נבנה מלבן כזה. למעשה, אפילו אין צורך לבנות את כל המלבן - אם הקטע הוא AB, והנקודה בחוץ היא C, אני מעביר אנך ל-AB מ-C, ואז מעביר אנך לישר שהתקבל שעובר דרך C והופס - בנינו את המקביל שלנו! שימו לב - הבניה הזו לא מוכיחה שהאובייקט שבנינו הוא מקביל; בשביל זה צריך להוכיח את הטענה על המלבן שטענתי קודם, וזה דורש אקסיומות ואקשן. אנחנו לא עוסקים כאן בהוכחות אלא בבניות, שמסתמכות על הידע התיאורטי שיש לנו.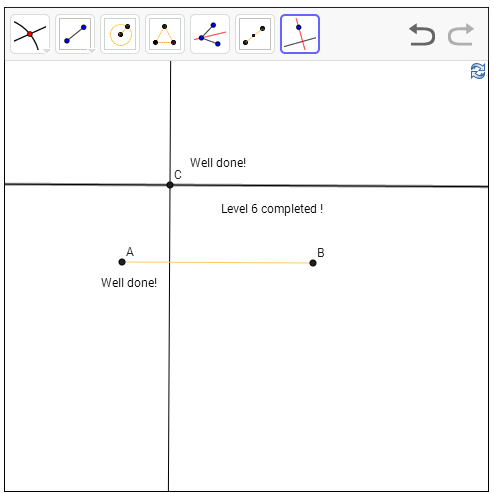

שלב 7 - העתקת קטע

כאן העסק מתחיל להיות מעניין, כי אנחנו רואים שאפשר לעשות דברים די חזקים עם הסרגל והמחוגה הללו - למשל, לקחת קטע קיים AB ו”להעתיק” אותו - כלומר, בהינתן נקודה C, לבנות קטע שיוצא מ-C באותו כיוון ובאותו אורך כמו AB. זה אומר שאפשר לבצע חלק מהבניות העתידיות שלנו “בצד” ואז להעתיק את התוצרים פנימה אל האקשן המרכזי. אבל איך נעשה את זה? לבנות ישר באותו כיוון כמו AB זה קל - זה מקביל, וכבר ראינו בדיוק איך בונים אותו וזה אחד מהכלים הבסיסיים שלנו. אבל מה עם האורך? אנחנו רוצים למצוא על המקביל שבנינו נקודה שמרחקה מ-C הוא בדיוק AB. ובכן, הבה ונגייס את הגאומטריה האוקלידית שוב לעזרתנו! אנחנו יודעים שבמקבילית, אורכי כל זוג צלעות מקבילות שווים, אז הבה ונבנה מקבילית: נחבר את C ל-A, נעביר מקביל לקטע הזה שעובר דרך B, והוא יחתוך את המקביל שכבר בנינו בנקודה שהיא הקודקוד האחרון של המקבילית; עכשיו נעביר במפורש קטע בין הקודקוד הזה ובין C, וסיימנו.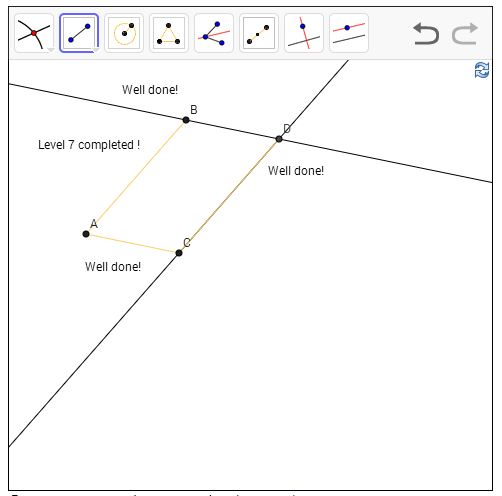

שלב 8 - בניית מעגל עם מרכז ואורך נתונים

מחוגה מאפשרת לנו לבנות מעגל עם מרכז נתון ונקודה נתונה שאמורה להיות על המעגל, אבל אנחנו רוצים יותר מזה - אם נתון לנו רדיוס כלשהו, בתור קטע שפזור לו אי שם ביקום, אנחנו רוצים לבנות מעגל שרדיוסו ארוך בדיוק כמו הקטע הזה, עם נקודת אמצע נתונה. הקאץ’ הוא שנקודת האמצע לא חייבת להיות מחוברת בשום צורה אל הקטע-שמייצג-את-אורך-הרדיוס. ובכן, אתם עשויים לשאול - אז מה? פשוט תעתיק את הקטע הזה על הנקודה… כן, זה הפתרון. זה עד כדי כך פשוט.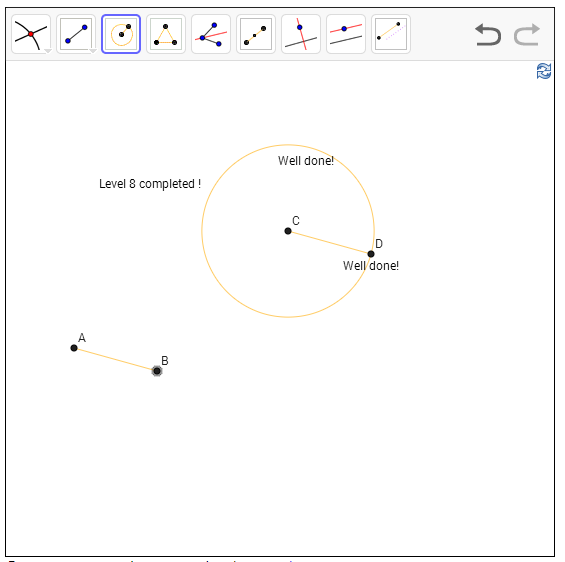

שלב 9 - העתקת אורך של קטע

מה שעשינו בשלב 7 היה להעתיק קטע AB באופן שמשמר גם את הזווית וגם את האורך שלו. עכשיו אנחנו רוצים לשמר את האורך, אבל שהזווית תהיה שרירותית ונתונה לנו על ידי קטע אחר כלשהו - טכנית, צריך לחתוך מהקטע הזה חתיכה שאורכה יהיה בדיוק AB. הדבר הראשון שמתבקש לעשות הוא להתחיל להדביק דברים ביחד. כרגע AB רחוק מהקטע CD שאנחנו רוצים לחתוך; אז אני מעתיק את AB ומדביק אותו על C - לקטע המתקבל קוראים CE. עכשיו כל מה שאני צריך, בעצם, הוא למצוא נקודה על CD שמרחקה מ-C הוא CE. כלומר, שמרחקה מ-C שווה למרחק E מ-C… כבר עשינו את זה לא אחת - פשוט מציירים מעגל.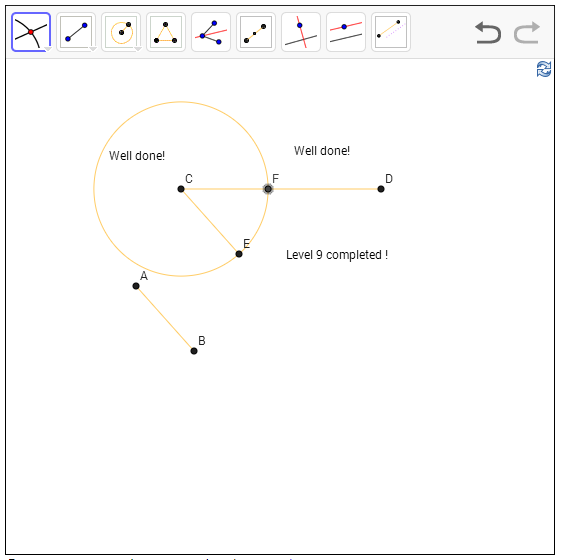

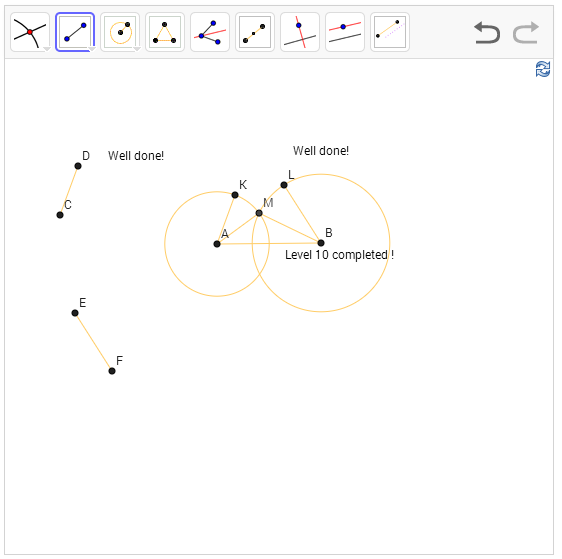
שלב 10 - בניית משולש עם אורכי קטעים נתונים

הפעם נתונים לנו שלושה מספרים, ואנחנו צריכים לבנות משולש שאורכי צלעותיו הם בדיוק המספרים הללו. המספרים נתונים בתור קטעים, אבל הזוויות שבהן הקטעים הללו נתונים הן לאו דווקא הזוויות שבהן צלעות המשולש יהיו - אם מנסים סתם להדביק עותקים של שני קטעים על הקצוות של השלישי, הקטעים “לא יתחברו” ולא נקבל משולש. שימו לב שבהינתן שלושה אורכי צלעות, המשולש שמתאים להן הוא יחיד: זה בדיוק מה שאומר משפט החפיפה של צלע-צלע-צלע. אבל איך נבנה אותו? ובכן, להתחיל בלחבר את שניים מהקטעים לקודקודים של השלישי זה בכל זאת לא רעיון רע. אחר כך עוצרים לחשוב שניה. קיבלנו שני קטעים AK וBL, שהיינו רוצים שיתחברו בקצה שלהם אבל הם לא - הנקודה K שונה מהנקודה L. מה שאנחנו רוצים למצוא הוא נקודה M, כך ש-AM שווה ל-AK, ו-BM שווה ל-BL. הנקודה הזו תהיה בדיוק הקודקוד הנוסף של המשולש. איך מוצאים אותה? כבר היינו במשחק הזה כמה פעמים - מעגלים.

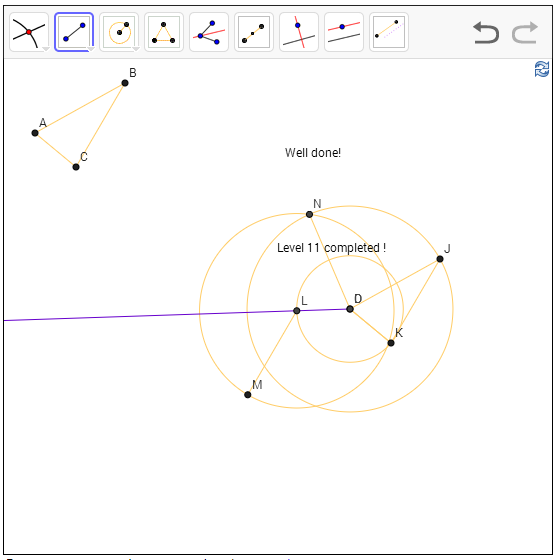
שלב 11 - העתקת זווית

כעת נתונה לנו זווית (על ידי שני קטעים) ונתון לנו ישר, ואנחנו צריכים לבנות את הזווית על הישר - כלומר, לבנות קטע שמתחבר לישר ויוצר איתו את הזווית הזו.

הפתרון הפעם יוצא טיפה מסורבל - אולי מישהו חושב על פתרון טוב יותר? מה שאני החלטתי להתבסס עליו הוא על חפיפת משולשים. אני מסתכל על המשולש ABC שמגדיר את הזווית (הזווית היא CAB), ואומר לעצמי - אם אצליח להעתיק אותו אל הישר, כך שהנקודה D על הישר תואמת את הנקודה A במשולש ואחת מצלעות המשולש יושבת על הישר, סיימתי.

אז הדבר הראשון שאני עושה הוא להשתמש ביכולת העתקת הקטעים שלי כדי להעתיק את המשולש ABC אל המשולש DKJ. הבעיה היא שאף צלע של המשולש לא יושבת על הישר.

אז הדבר הראשון שאני עושה הוא ליצור צלע מתאימה על הישר - אני מעביר מעגל שמרכזו ב-D ורדיוסו נוגע ב-K, ומסמן את החיתוך שלו עם הישר ב-L. עכשיו הקטע DL חופף לקטע DK. נשאר לטפל בשתי הצלעות האחרות. בשבילן אני אצטרך קודקוד חדש. נקרא לו N. אני צריך מ-N שני דברים: ראשית, ש-DN יהיה שווה ל-DJ. אז N יהיה על מעגל שמרכזו ב-D ועובר דרך J. זה קל. מה יותר מסובך? אני צריך ש-LN יהיה שווה באורכו ל-KJ. אז אני קודם כל מעתיק את KJ ושם אותו על L, ומקבל את הקטע LM; ואז אני מעביר מעגל מ-L שעובר דרך M, וחותך אותו עם המעגל השני, ומקבל את N שלי.

זה לא נראה טוב. אבל היי, זה עובד.

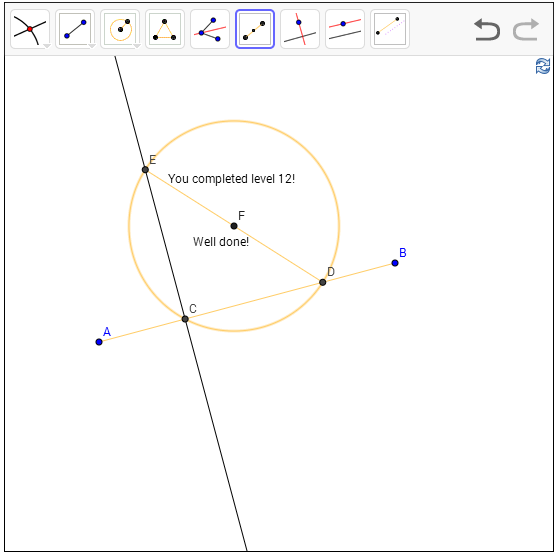
שלב 12 - מציאת מרכז של מעגל

הפעם הנתונים שלנו מאוד מינימליסטיים - אין נקודות בכלל, רק מעגל. ואנחנו צריכים ליצור יש מאין את נקודת המרכז שלו. באיזה כלי נשק כדאי להשתמש?

מה שלי נראה כמו זווית תקיפה טובה הוא מציאת קוטר. אם אצליח לבנות קטע שהוא קוטר של המעגל, המרכז יהיה בדיוק נקודת האמצע של הקוטר.

ואיך מוצאים קוטר? שוב, כדאי להכיר משפטים מגאומטריה. במקרה הזה: זווית היקפית במעגל שהיא ישרה (בת 90 מעלות) נשענת על קוטר. מה זה זווית היקפית? קחו שני מיתרים במעגל שנפגשים בנקודה שעל המעגל - הזווית שהם יוצרים נקראת “זווית היקפית”. הקטע שסוגר את המשולש - מחבר את שתי נקודות החיתוך הנוספות של המיתרים עם המעגל - הוא הצלע שהזווית ההיקפית “נשענת” עליה.

אז מה שעושים הוא פשוט: אני חייב נקודות על המעגל, אז אני בונה קטע שחותך אותו. לקטע הזה אני מעביר אנך באחת מנקודות החיתוך, והנה קיבלתי זווית ישרה. אני מחבר את נקודות החיתוך עם המעגל של שני הישרים שבניתי, לוקח את האמצע - והופס, נפתר.

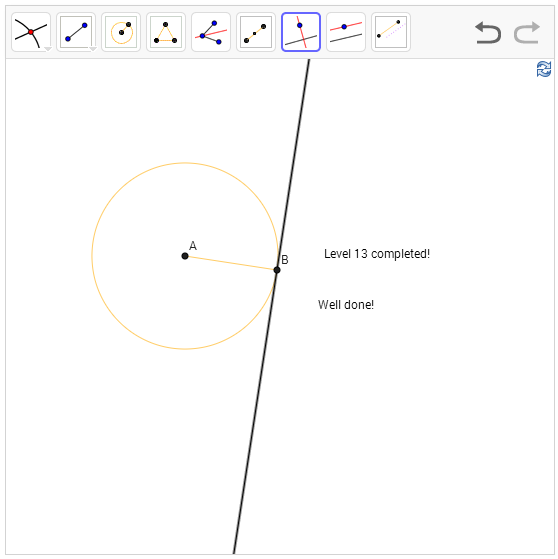
שלב 13 - מציאת משיק למעגל בנקודה נתונה

נתון לנו מעגל על ידי מרכז ונקודה שעליו. צריך למצוא משיק בנקודה הזו. זה טריוויאלי לגמרי אם זוכרים עוד משפט על מעגלים - משיק למעגל מאונך לרדיוס בנקודת ההשקה. אז אני מעביר את הרדיוס ומעביר משיק לרדיוס. זהו.

שלב 14 - בניית מעגל חסום במשולש

עכשיו נתון לנו משולש ואנחנו מתבקשים למצוא את המעגל שחסום בו - כלומר, ששלושת צלעות המשולש משיקות אליו.

כאן אין חוכמה. מי שמכיר את המשפט שמאפיין מעגל כזה יכול לסיים את הבניה מייד. מי שלא… כנראה ישבור את הראש או ינסה הרבה דברים. המשפט קל להבנה: מרכז המעגל החסום במשולש הוא נקודת המפגש של שלושת חוצי הזוויות. מרגע שיש לנו את זה, הבניה מיידית - בונים את חוצי הזווית (אנחנו כבר יודעים לעשות את זה), מוצאים את נקודת החיתוך שלהם, מעבירים ממנה אנך לאחת מצלעות המשולש (כי זכרו - זה אמור להיות רדיוס, והרדיוס מאונך למשיקים) ואז מציירים מעגל שמרכזו בנקודת החיתוך של חוצי הזוויות ועובר דרך נקודת החיתוך של האנך עם צלע המשולש.

אבל למה המשפט על חוצי הזוויות נכון בכלל? זו הרי השאלה האמיתית כאן. הסיבה פשוטה: לחוצה זווית במשולש יש את התכונה שכל נקודה שעליו מרוחקת משתי הצלעות של הזווית באותה מידה. מה זה אומר “מרוחקת”? מרחק נמדד על ידי הורדת אנך ומדידת אורכו. לכן נקודת החיתוך של כל חוצי הזוויות היא נקודה שהמרחק שלה (על ידי הורדת אנך) מכל צלעות המשולש הוא זהה - ולכן האנכים הם רדיוסים של מעגל אחד והכל מסתדר.

אבל למה כל נקודה על חוצה הזווית מרוחקת משתי הצלעות באותה המידה? נסו לצייר את הסיטואציה ותראו חיש קל: אחרי הורדת שני האנכים מתקבל דלתון, וחוצה הזווית חוצה אותו לשני משולשים. המשולשים הללו זהים בזוויות שלהם (כי זווית אחת היא ישרה ושוויון זוג זוויות אחר מובטח על ידי חוצה הזווית) ויש להם צלע משותפת, ולכן הם חופפים.

התרגיל הזה הוא לטעמי התרגיל הלא טריוויאלי ממש הראשון במשחק; כאמור, איני חושב שמי שאינו מכיר את המשפט (ואינו משופשף בגאומטריה באופן כללי) יכול להגיע בעצמו לפתרון, ואין בחוסר היכולת הזה כל רע, כמובן.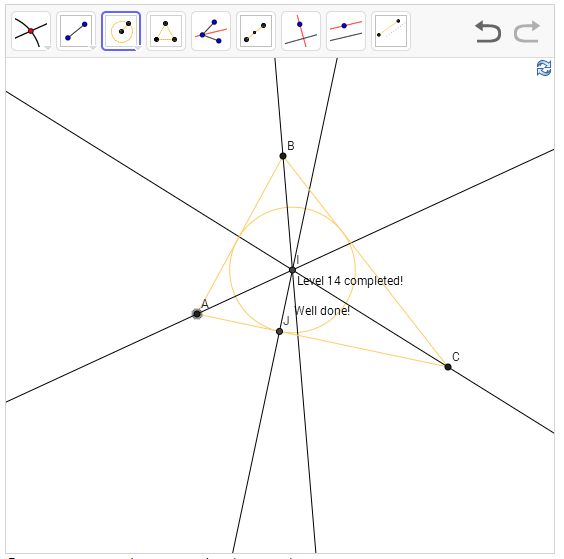

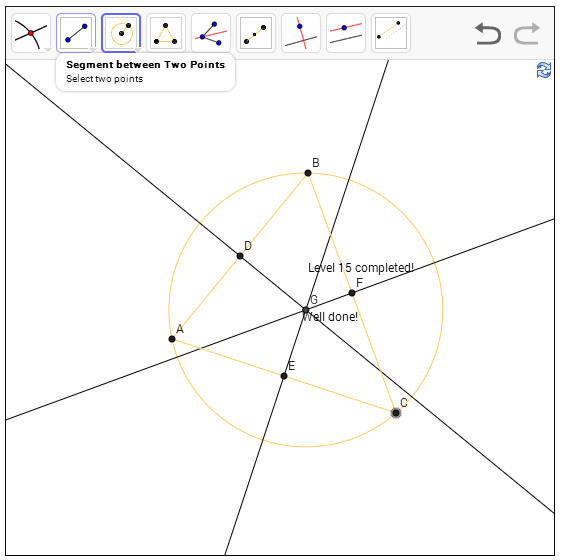
שלב 15 - בניית מעגל חוסם משולש

נתון לנו משולש - אנחנו רוצים להעביר מעגל שעובר דרך כל קודקודיו (לא חייבים לחשוב על זה בתור משולש אפילו - הטענה הכללית היא שדרך כל שלוש נקודות עובר מעגל יחיד, ועכשיו אנחנו מתבקשים למצוא אותו).

כמקודם, מי שמכיר את התעלול פותר בקלות - מרכז המעגל הוא נקודת המפגש של האנכים האמצעיים במשולש (אנך אמצעי הוא אנך לצלע שהוא גם תיכון לצלע). מה ההגיון כאן? ובכן, מרכז המעגל צריך להיות מרוחק מכל הקודקודים במידה שווה. בואו ניקח שני קודקודים, AB. מהו אוסף כל הנקודות שמרוחק באותה מידה מ-A ומ-B? ראשית, הוא כמובן כולל את נקודת האמצע של הקטע AB, שבואו נסמן D. שנית, אם G היא נקודה כלשהי כך ש-AG שווה ל-BG, אז המשולש ABG הוא שווה שוקיים, ולכן הקו המחבר את G (הקודקוד העליון של המשולש הזה) עם D הוא תיכון; ותיכון במשולש שווה שוקיים הוא גם אנך. מסקנה: G נמצאת על האנך ל-AB שעובר דרך אמצע AB. מכאן שמפגש האנכים האמצעיים במשולש הוא הנקודה היחידה במשולש שמרחקה מכל הקודקודים זהה, כנדרש.

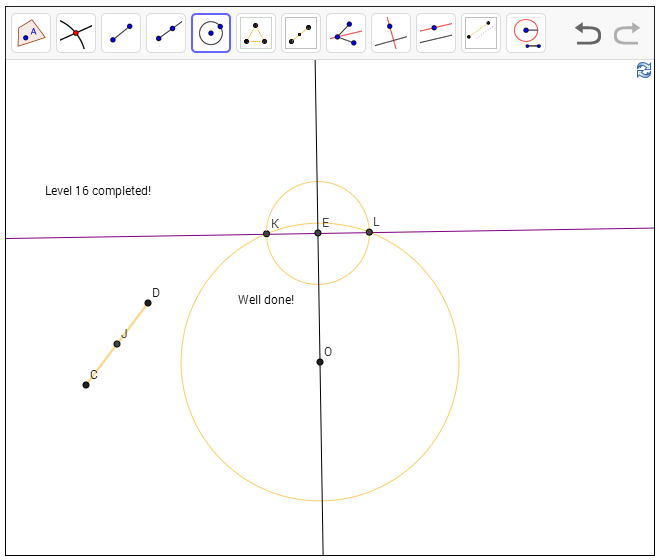
שלב 16 - בניית מעגל שהחיתוך שלו עם ישר נתון שווה לגודל קטע נתון

נתון לנו אורך - שוב, על ידי קטע CD כלשהו - ונתונה לנו נקודה O וישר. המטרה שלנו - לבנות מעגל שמרכזו ב-O שהחיתוך שלו עם הישר הוא בדיוק מגודל CD.

התרגיל הזה פשוט יחסית בואו נקרא לנקודות החיתוך K,L. אנחנו רוצים ש-KL יהיה שווה באורכו ל-CD. אז אנחנו רוצים למקם קטע מאורך CD על הישר הנתון. אבל איפה? מכיוון ש-OK צריך להיות שווה ל-OL, המשולש שיווצר על ידי הרדיוסים הללו והקטע KL יהיה שווה שוקיים - ולכן האנך לבסיס במשולש הזה הוא גם תיכון. אז הדבר הראשון שאני עושה הוא להעביר אנך לישר מ-O ולקרוא לנקודת החיתוך E; עכשיו אני יודע ש-K ו-L צריכים להיות מרוחקים מ-E באותו מרחק בדיוק. למצוא אותם זה עניין פשוט - אני משתמש בכלי שכבר יש לי שמאפשר לבנות מעגל עם מרכז נתון (E) ורדיוס שנתון בתור אורך של קטע; רק שאני לא רוצה רדיוס CD כי זה ארוך מדי - אני צריך חצי מזה. לכן אני קודם כל משתמש בכלי שלי שיודע לחצות את CD לשניים.

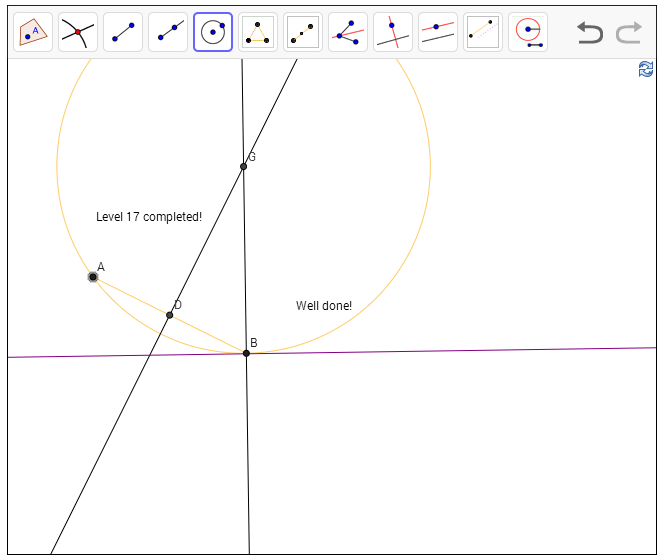
שלב 17 - בניית מעגל העובר דרך נקודה אחת ומשיק לישר בנקודה אחרת

נתונות לנו נקודות A,B כך ש-B נמצאת על ישר. מבקשים למצוא מעגל שעובר דרך A ו-B ומשיק לישר ב-B. וזה… קל בצורה מפתיעה, למען האמת. רק צריך למצוא את מרכז המעגל, כי אנחנו יודעים שהוא חייב לעבור דרך A,B.

אנחנו יודעים שרדיוס בנקודת ההשקה B חייב להיות מאונך לישר, אז נעביר אנך לישר בנקודה B. עכשיו אנחנו יודעים שהמרכז של המעגל חייב להיות על האנך הזה. עכשיו, מכיוון שהמעגל עובר גם ב-A וגם ב-B, הרי ש-OA=OB ולכן המשולש OAB הוא שווה שוקיים, ולכן האנך גם חוצה את AB… כבר היינו בסיפור הזה. אז מותחים את AB, מחלקים אותו לשניים, מעבירים אנך, ומרכז המעגל שאנו מחפשים הוא החיתוך בין האנך הזה לאנך שכבר ציירנו קודם.

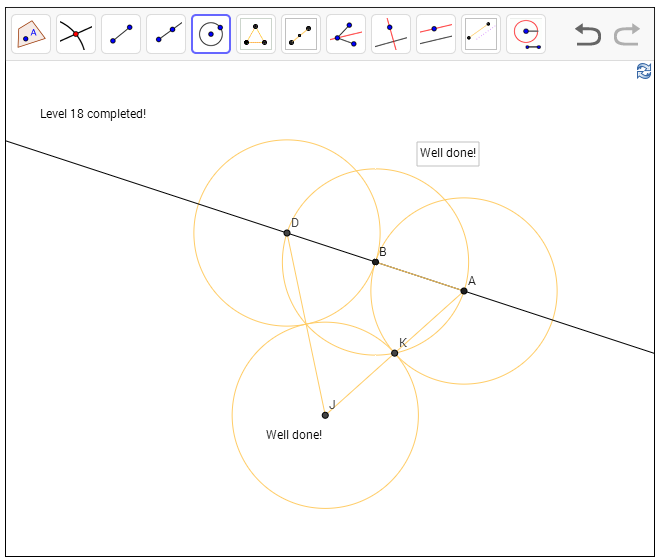
שלב 18 - בניית שלושה מעגלים בעלי אותו רדיוס שכולם משיקים זה לזה

כאן נותנים לנו מראש את אחד המעגלים על ידי מרכז A ונקודה שעליו B, ומבקשים שאחד מהמעגלים משיקים האחרים יעבור דרך הנקודה הזו.  את המעגל הזה קל מאוד לבנות - רק צריך להמשיך את AB באותו כיוון ובאותו אורך. משום הוא לא הצלחתי לעשות את זה בעזרת הפעולה הקיימת, אז פשוט יצרתי מעגל שמרכזו B ועובר דרך A ובדקתי איפה הוא חותך את המשך AB.

המעגל השלישי קצת יותר טריקי, אבל אם שולפים את טיעון הקסם “שיקולי סימטריה” רואים שהמרכז שלו הוא הקודקוד השלישי במשולש שווה צלעות שמרכזי שני המעגלים האחרים הם קודקודיו האחרים. זה מסיים את זה.

שלב 19 - חלוקת קטע לשלושה חלקים

כאן האקשן האמיתי מתחיל. אני אציג פתרון אחד, שהוא יחסית כללי, ואני בטוח שיש עוד פתרונות אלגנטיים ופשוטים יותר; עם זאת, לפתרון “שלי” יש יתרון שנובע מהכלליות שלו (וחוץ מזה, זה מה שהצלחתי להמציא ואני די מרוצה מכך שפתרתי בלי לפתוח רפרנס).

הרעיון שלי בעצם מסביר איך אפשר לבצע חילוק כללי של קטעים: בהינתן שני קטעים מאורכים A ו-B, אני בונה קטע חדש מאורך A/B. בשיטה דומה אפשר לבצע כפל. כמו כן כבר ראינו בהתחלה שאפשר לבצע חיבור (זה היה ה”שכפול” של קטע) ובשיטה דומה אפשר לבצע חיסור, כך שאנחנו רואים שאפשר לבצע את ארבע פעולות החשבון עם המספרים שמתארים אורכים של קטעים. זה אומר שאוסף המספרים שהם אורכים של קטעים שניתנים לבניה עם סרגל ומחוגה - או בקיצור, ניתנים לבניה - מהווים שדה. זה השלב הראשון בדרך להוכחה שהזכרתי בראשית הפוסט, אבל נעזוב את זה לבינתיים.

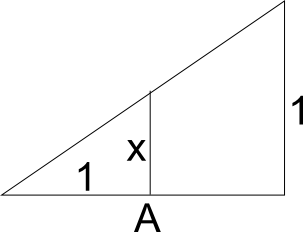
אז מה התעלול שאני משתמש בו כדי לבצע חילוק? בשתי מילים - דמיון משולשים. נניח שיש לי קטע מאורך A ואני רוצה לבנות את אחד חלקי A. איך לעשות את זה? אני אבנה משולש ישר זווית שאורך אחת הרגליים שלו הוא בדיוק A ואורך השניה בדיוק 1, ואז אעביר אנך בדיוק אחרי מרחק של 1 מקודקוד המשולש. הנה איך שזה נראה בציור:

קיבלנו כאן בבירור שני משולשים דומים: הם חולקים זווית אחת, וזווית אחרת היא בת תשעים מעלות. בהערת אגב, בכל פעם שבה אני מצייר את המשולש הזה אני לא יכול שלא להיזכר במקום הראשון שבו למדתי על התעלול הזה - בספר “אי המסתורין” של ז’ול ורן, משתמשת אחת הדמויות במשולש כדי כדי להעריך גובה של מצוק (אבל לא כדי לחלק דברים עם סרגל ומחוגה). אין לי מושג אם זה עובד בפועל ככה, אבל בתור נער ממש התלהבתי מהעניין הזה ובפעם הראשונה הבנתי למה משולשים דומים זה מעניין. תודה, ז’ול!

עכשיו, בין שני משולשים דומים הצלעות שמול אותן זוויות יכולות להיות שונות אבל הפרופורציה בין האורכים שלהן נשמרת. במקרה שלנו 1 חלקי x יהיה אותו הדבר כמו A (האורך הכולל של הצלע התחתונה) חלקי 1. חישוב מהיר יראה לנו שאם כן, x חייב להיות 1 חלקי A. הצלחנו לחלק! תגידו לי שזה לא מגניב, נראה אתכם!

עכשיו, ודאי תשאלו - מה זה “1”? אין לי קטע מאורך “1” בבעיה שנתנו לי. אבל זה כמובן לא משנה - אפשר לשים כל גודל במקום ה-1 הזה, ופשוט במקום לקבל 1 חלקי משהו, נקבל את הגודל חלקי משהו. לי בכל זאת חשוב היה לכתוב כאן 1 כי אני רוצה להבהיר שהסימון “1” בהקשר הגאומטרי הוא שרירותי - אני יכול לקחת קטע כלשהו, לקרוא לאורך שלו “1”, ומכאן ואילך שאר הקטעים נמדדים לפיו.

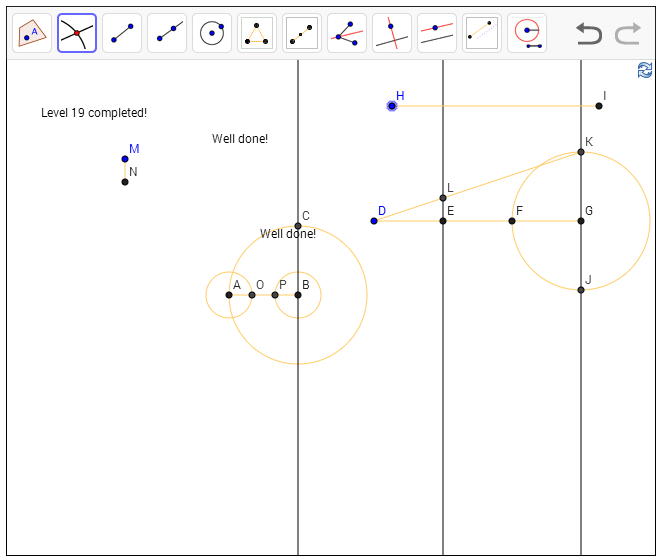
אז איך פתרתי את השאלה? ראשית, לקחתי את הקטע AB שנתנו לי (ואני חושב עליו בתור אורך 1) והעתקתי אותו הצידה. חיברתי שלושה עותקים שלו בזה אחר זה וקיבלתי קו מאורך 3 DG, שכבר מחולק באופן נוח לשלושה קטעים מאורך 1. על הקטע הזה בניתי משולש ישר זווית כמו באיור שלמעלה - אני יודע להעביר אנך, והשתמשתי במעגל כדי לוודא שגובה הצלע המאונכת יהיה 1 גם כן, ואז חיברתי אותה ל-D וקיבלתי את היתר של המשולש, הרמתי אנך מ-E אל היתר (למה מ-E? כי אורך DE הוא 1), חתכתי וקיבלתי קטע LE שאורכו הוא שליש. זה בדיוק מה שרציתי!

את ה-1/3 הזה העתקתי הצידה (זה MN שאתם רואים שם) ואז בניתי על AB שני מעגלים - אחד סביב A והשני סביב B - שרדיוס כל אחד מהם הוא 1/3. חתכתי אותם עם AB, וסיימנו.

זה היה ממש כיף!

שלב 20 - העברת משיק לשני מעגלים נתונים

כולם הזהירו ששלב 20 יהיה קשה בצורה חריגה ביחס ליתר, ואכן הוא היה כזה, אבל בסופו של דבר, אחרי ששברתי את הראש על השלב הזה לא מעט, הפתרון יצא לי קל משחשבתי מלכתחילה. זה עדיין לא פתרון טריוויאלי ויהיה מעניין לשמוע אחרים.

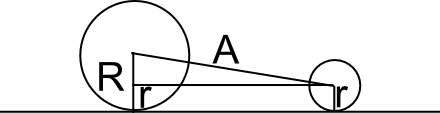
נתחיל עם השרטוט שפתר לי את התרגיל - אני מתחיל מלצייר את המשיק בתור קו אופקי, ואז מצייר את המעגלים עליו ורואה מה קורה:

אני מסמן את הרדיוס של המעגל הקטן ב-r, את הרדיוס של המעגל הגדול ב-R ואת אורך הקטע שמחבר ביניהם ב-A. הרדיוסים מאונכים למשיק ולכן אנחנו מקבלים מלבן עם אורך צלע r, ומעליו משולש ישר זווית עם יתר A ועם אורך צלע אחת שהוא R-r. אורך הצלע השניה, שהוא אורך הצלע האחרת של המלבן, הוא תעלומה, אבל ניתן לחשב אותו מתוך משפט פיתגורס. אבל לא באמת צריך להכיר את משפט פיתגורס כאן: מספיק שאני אבנה עם סרגל ומחוגה את R-r, אעביר אליו אנך, ואחתוך את האנך הזה עם מעגל ברדיוס A כדי למצוא את האורך של הצלע האחרת ההיא, שאקרא לו B.

איך למצוא את B יעזור? זה טוויסט נוסף: אני יודע שהצלע העליונה של המלבן משיקה למעגל ברדיוס r שמצויר בתוך המעגל מרדיוס R; לכן אם אבנה מעגל מרדיוס B שמרכזו כמרכז המעגל הקטן, נקודות החיתוך שלו עם המעגל מרדיוס r שבתוך המעגל הגדול יהיו בדיוק נקודות ההשקה. ואז אעביר את המשיק, אוריד אנכים ממנו, אחתוך עם המעגלים, אעביר קו בין המעגלים, וסיימתי (אפשר לראות את כל זה בתמונה).

הבעיה היחידה שנותרה היא איך לחשב את R-r. זה למען האמת די פשוט - מעתיקים את הקטע באורך R הצידה; מציירים על אחד מקצותיו מעגל ברדיוס r; מה שנשאר מחוץ למעגל הוא R-r.

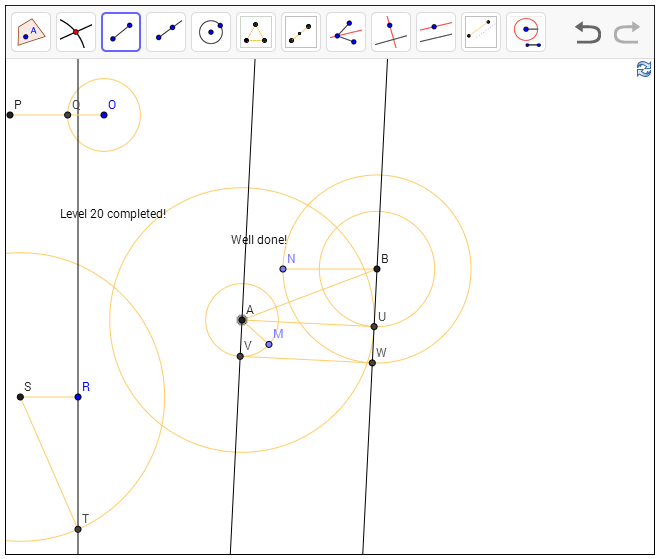
אסביר עכשיו מה בדיוק הולך בצילום המסך שלי. ראשית העברתי קו מ-A אל המעגל הראשון כדי לקבל את האורך של הרדיוס של המעגל, r. אותו הדבר עשיתי ב-B כדי לקבל את R. אחר כך העתקתי את BN ל-OP כדי לקבל קטע חדש בצד (משמאל למעלה) מאורך R, וציירתי עליו מעגל ברדיוס r שחתך את OP ב-Q. אם כן, הקטע PQ הוא בדיוק מאורך R-r.

עכשיו האקשן עובר למשולש בצד שמאל למטה. כאן RS הוא העתקה של PQ. בניתי אנך אליו. העברתי מעגל שמרכזו ב-S ורדיוסו הוא AB, ונקודת החיתוך עם האנך נקראה T. אם כן, RT הוא האורך שחיפשתי.

כעת העברתי מעגל ברדיוס r עם מרכז B, וחתכתי אותו עם מעגל ברדיוס RT שמרכזו A. נקודת החיתוך, U, היא בדיוק נקודת ההשקה של המשיק שיוצא מנקודה A למעגל ברדיוס r עם מרכז B. ציירתי את המשיק הזה, העברתי אנכים אליו שעוברים דרך A,B, חתכתי עם המעגלים וקיבלתי את V,W - הנקודות שדרכן יש להעביר את המשיק המשותף.

לא פשוט - אני בטוח שיש דרך יותר אלגנטית, וכנראה גם אפשר לפשט את הרעיון שלי - אבל גם לא כל כך נורא.

אני חושב שאפשר לסכם שהמשחק הזה היה כיף חיים. נקווה שיוסיפו שלבים בהמשך.