מבוא לאפקטים קוונטיים על קצה המזלג

אצהיר מראש: הבלוג הזה אינו בלוג פיזיקה ואין לי שליטה מספקת בחומר כדי לכתוב פוסטים בפיזיקה. עם זאת, אין לי מנוס מלכתוב אחד עכשיו, כי לפני שנותנים מבוא לחישוב קוונטי צריך לתת תיאור כללי של הרקע, גם אם אחר כך לא נשתמש בו יותר מדי. אז קחו בחשבון את הסכנה שהפוסט הזה יהיה לא מדויק אפילו יותר מאשר בדרך כלל, אבל אני מקווה שאצליח להעביר את רוח הדברים בצורה נכונה. על מנת להדגיש את רוח החובבנות של הפוסט, גם האיורים שעשיתי נראים פשוט איום ונורא ולא התאמצתי יותר מדי לוודא שהם מדוייקים (והם לא).

אני רוצה לתת כאן דוגמאות לשני ניסויים שממחישים את תורת הקוונטים, את האופי המוזר שלה וטיפה מהפורמליזציה המתמטית שלה. המטרה בניסויים הללו היא לא לשכנע אתכם שתורת הקוונטים נכונה - יש לה מספיק קבלות בעולם האמיתי והיא לא צריכה אותי בשביל זה - אלא להבין מה זו בכלל תורת הקוונטים.

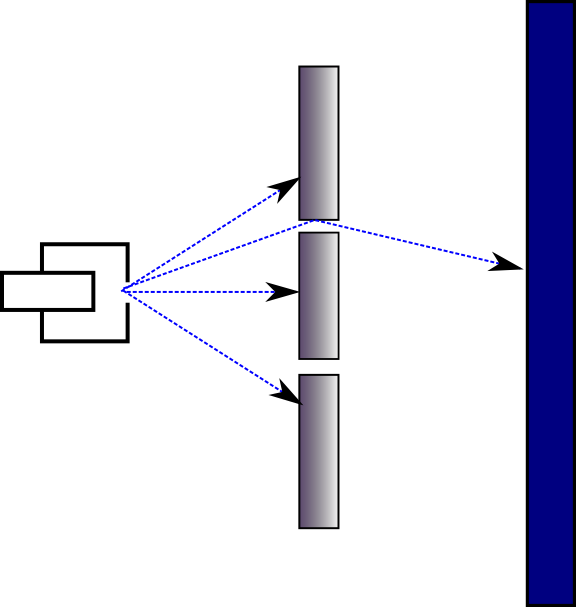
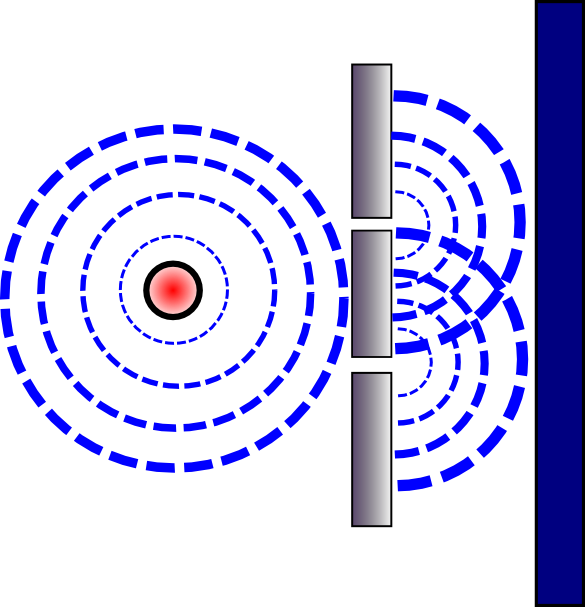
הניסוי הראשון נקרא “ניסוי שני הסדקים”, והוא תואר על ידי ריצ’רד פיינמן בהרצאות שלו על תורת הקוונטים (הכרך השלישי בסדרת Feynman Lectures on Physics). הניסוי עצמו הוא ישן למדי - הוא הומצא במאה ה-19 בידי תומס יאנג - אבל פיינמן משתמש בוריאציה עליו כדי לסייע בתיאור עקרונות תורת הקוונטים. הרעיון הבסיסי הוא זה: יש לנו מקור ש”יורה” עוד ועוד אובייקטים מסוג כלשהו - בהתחלה פיינמן מדבר על קליעי רובה, אחר כך על גלי מים ובסופו של דבר על אלקטרונים - אל עבר קיר שיש בו שני סדקים שרק דרכם החלקיקים יכולים לעבור. מהצד השני של הקיר יש גלאי שמאפשר לנו לראות לאן החלקיקים הגיעו בסופו של דבר, ואנו מנסים לראות איזו תבנית נוצרת על הקיר. כך זה נראה באיור:

פיינמן מניח שמקור החלקיקים יורה אותם “קדימה”, אבל בפיזור כלשהו (ההסתברות לזווית פיזור יורדת ככל שזווית הפיזור גדלה). כפי שאפשר לראות, חלקיק שנורה ממש קדימה פשוט ייתקע במחסום ולא יגיע לגלאי; מה שמעניין אותנו הם חלקיקים שמגיעים לסדקים ועוברים דרכם, או מתנגשים בהם וניתזים לכיוון השני ובסוף פוגעים באמצע הגלאי, באיזור שלכאורה “מוסתר” על ידי המחסום (כמו בתמונה). אפשר למדוד כמה קליעים הגיעו לכל נקודה בגלאי ולצייר גרף שמתאר את הכמות שלהם ביחס לכמות הכוללת של קליעים שהגיעו אל הגלאי, מה שמאפשר לנו לראות איזורים שנפגעים יותר ופחות (בצורה ציורית - איזורים בגלאי שהם “מלאים חורי קליעים” ואיזורים שפחות). כשמציירים את העקומה שמתאימה לניסוי של פיינמן היא נראית קצת מוזרה במבט ראשון - הכמות הגדולה ביותר של קליעים מגיעה למרכז, לאיזור שלכאורה מוסתר על ידי המחסום, והיא הולכת וקטנה ככל שהולכים לצדדים:

(אגב, זו העקומה אצל פיינמן, אבל מקומות אחרים שמתארים את הניסוי נותנים עקומה שונה, שבה המרכז הוא לא קטן אבל לא גדול כמו ה”פסגות” שמול הסדקים; אני בחרתי להיות נאמן לפיינמן).

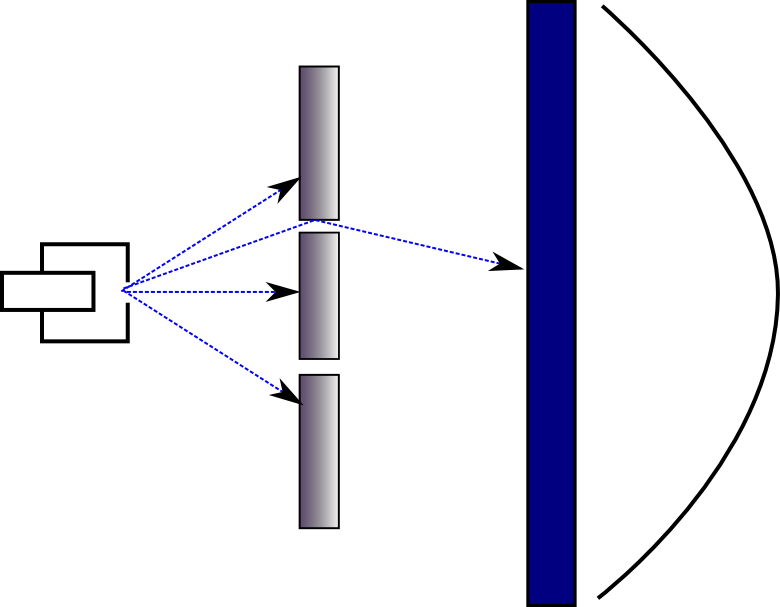
כדי להבין את התופעה הזו, פיינמן מציע להסתכל על הקליעים שעברו דרך כל סדק בנפרד. כדי לעשות את זה אפשר לחסום באופן זמני את אחד הסדקים, ולראות מה התבנית שמתקבלת כשרק הסדק השני פתוח. בשל הסימטריה של המערכת אנו מקבלים תבנית דומה לכל אחד מהסדקים, ובצורה לא מפתיעה במיוחד גם התבנית הזו היא “חזקה במרכז וקטנה ככל שהולכים הצידה”, אבל כאן המרכז שלה הוא באיזור שאליו מגיעים קליעים שפשוט עוברים דרך הסדק בלי להתנגש בו:

מה שקורה כשפותחים את שני הסדקים הוא שהעקומה שאנחנו מקבלים היא התוצאה של חיבור שתי העקומות עבור הסדקים:

בואו נניח ש-\( x \) היא נקודה כלשהי על הגלאי. נסמן ב-\( P_{x} \) את ההסתברות שקליע יגיע אל הנקודה הזו כשהוא נורה מהמקור. את ההסתברות הזו אפשר לפרק לשניים: נסמן ב-\( P_{x}^{1} \) את ההסתברות שהקליע יעבור בסדק מס’ 1 ויגיע ל-\( x \), וב-\( P_{x}^{2} \) את ההסתברות שהוא יעבור בסדק מס’ 2 ויגיע ל-\( x \). \( P_{x} \) מתאר את העקומה ה”כללית”, בעוד ש-\( P_{x}^{1},P_{x}^{2} \) מתארים את העקומות של כל אחד מהסדקים בנפרד, ומתקיים \( P_{x}=P_{x}^{1}+P_{x}^{2} \) מכיוון ש-\( P_{x}^{1},P_{x}^{2} \) הם מאורעות זרים ומשלימים, דהיינו לא ייתכן שקליע עובר הן דרך סדק 1 והן דרך סדק 2 ומגיע ל-\( x \), והוא חייב לעבור דרך אחד מהסדקים הללו כדי להגיע ל-\( x \). כמובן, אלו הנחות שאתם יכולים לחלוק עליהן ואפשר לעשות ניסויים מתוחכמים שבודקים אם הן נכונות (כי מי יודע, אולי הקליעים הם כמו “קליע הקסם” הידוע מתיאוריות הקונספירציה על התנקשות קנדי, והם כן עוברים דרך סדק אחד, חוזרים, עוברים דרך הסדק השני, עוברים את המחסום בלי לעבור באף סדק ובסוף מתפזרים לכמה חלקים ויוצרים תבנית מוזרה על הקיר?) אבל מהנסיון היומיומי שלנו עם קליעים אנחנו יודעים שההנחות נכונות. אם כן, זה האופן שבו קליעים “קלאסיים” מתנהגים בניסוי שני הסדקים - כל קליע עובר דרך חור אחד, והסתברות הפגיעה במקום מסויים היא סכום הסתברויות הפגיעה באותו מקום תוך מעבר בסדק ספציפי.

עכשיו אנחנו משנים את הניסוי ובמקום לירות קליעים אנחנו מעבירים משהו אחר דרך הסדקים - גלי מים. כמו קליעים, גם גלים הם משהו שאנחנו מכירים היטב מחיי היום יום, למרות שהמתמטיקה שלהם קצת יותר מסובכת להבנה מאשר קליעים. לא אכנס לעובי הקורה הפורמלי כי זה סיפור בפני עצמו; הרעיון מאחורי גל מחזורי הוא שמדובר על הפרעה שמתפשטת במרחב (איך בדיוק? תלוי בגל). בצורה פשטנית משהו אפשר לתאר את הערך של גל בנקודה מסויימת במרחב על ידי הנוסחה הבאה, שמתארת את הגל כפונקציה של הזמן \( t \): \( Ae^{i\left(\omega t+\phi\right)} \). גל כזה מאופיין על ידי שלושה מרכיבים: יש לו אמפליטודה \( A \), והערכים שהגל מקבל “מזפזפים” בין \( A \) ובין \( -A \); יש לו תדירות \( \omega \) שמתארת כמה מהר הוא “מזפזפ” בין הערכים הללו; ויש לו פאזה \( \phi \) שמתארת “באיזה גובה הגל מתחיל” בזמן \( 0 \). שימו לב שאני מתאר את הגל באמצעות אקספוננט מרוכב: \( e^{i\theta}=\cos\theta+i\sin\theta \). זו “רמאות” טכנית סטנדרטית שפיזיקאים משתמשים בה - בהקשר הזה אנחנו לא מתעניינים בחלק המרוכב של המספר אלא רק בחלק הממשי שלו, אבל החשבונות יותר נוחים כשמשתמשים באקספוננט מרוכב. גם לסיפור הזה אני לא הולך להיכנס כרגע.

כאשר אנחנו מודדים גל, אנחנו מודדים את העוצמה שלו, ששווה לערך המוחלט שלו בריבוע, או לכפל שלו בצמוד המרוכב שלו. עבור \( Ae^{i\left(\omega t+\phi\right)} \) מקבלים פשוט את העוצמה \( I=A^{2} \); העסק נהיה מעניין כשאנחנו רוצים למדוד את העוצמה של שני גלים שמתנגשים. מה שקורה הוא שגלים שמתנגשים יכולים “לקלקל” אחד לשני את העוצמה ואפילו לבטל זה את זה לחלוטין. בואו נראה את זה מתמטית: נניח ש-\( A_{1}e^{i\left(\omega t+\phi_{1}\right)} \) הוא גל אחד ו-\( A_{2}e^{i\left(\omega t+\phi_{2}\right)} \) הוא גל שני. שניהם בעלי אותה תדירות \( \omega \) כדי לשמור על הניתוח המתמטי פשוט, אבל האמפליטודה והפאזה שלהם יכולות להיות שונות. התוצאה של ההתנגשות של שני הגלים הללו היא גל שהוא פשוט הסכום של שניהם: \( A_{1}e^{i\left(\omega t+\phi_{1}\right)}+A_{2}e^{i\left(\omega t+\phi_{2}\right)} \). מה העוצמה של הגל הזה? הכי פשוט לכפול את הגל בצמוד שלו. קל לראות שנקבל סכום של ארבעה איברים: \( A_{1}^{2},A_{2}^{2} \) הפשוטים וכמו כן

\( A_{1}e^{i\left(\omega t+\phi_{1}\right)}\cdot A_{2}e^{-i\left(\omega t+\phi_{2}\right)}=A_{1}A_{2}e^{i\left(\phi_{1}-\phi_{2}\right)} \)

ובדומה, \( A_{1}A_{2}e^{i\left(\phi_{2}-\phi_{1}\right)} \) יהיה הרכיב הרביעי. את הסכום של שני הרכיבים הללו אפשר לפשוט קצת בעזרת הנוסחה \( \cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2} \) ולקבל:

\( A_{1}A_{2}e^{i\left(\phi_{1}-\phi_{2}\right)}+A_{1}A_{2}e^{i\left(\phi_{2}-\phi_{1}\right)}=2A_{1}A_{2}\cos\left(\phi_{1}-\phi_{2}\right) \)

כלומר, קיבלנו שעוצמת הגל שנוצר מה”התנגשות” היא \( A_{1}^{2}+A_{2}^{2}+2A_{1}A_{2}\cos\left(\phi_{1}-\phi_{2}\right) \), ואם נשתמש ב-\( I,I_{1},I_{2} \) כדי לתאר את עוצמות הגלים, קיבלנו את המשוואה

\( I=I_{1}+I_{2}+2\sqrt{I_{1}I_{2}}\cos\left(\phi_{1}-\phi_{2}\right) \)

שימו לב מה קורה כאן: בגלים עם הפרש פאזה 0, הגלים מחזקים זה את זה. ככל שהפרש הפאזה גדל, כך ה”תמיכה” שמתקבלת מהרכיב \( 2\sqrt{I_{1}I_{2}}\cos\left(\phi_{1}-\phi_{2}\right) \) הולכת וקטנה, עד שהפרש הפאזה מגיע ל-90 מעלות ואז הוא מתאפס ועוצמת הגל היא בדיוק \( I_{1}+I_{2} \); מכאן והלאה ככל שהפרש הפאזות גדל כך הרכיב \( 2\sqrt{I_{1}I_{2}}\cos\left(\phi_{1}-\phi_{2}\right) \) הוא שלילי ולכן הוא מקטין את העוצמה הכוללת של הגל.

זו תופעה מעניינת: אינטואיטיבית, היינו מצפים כנראה שהעוצמה של שני הגלים שהתנגשו תהיה תמיד \( I_{1}+I_{2} \), סכום העוצמות של הגלים המתנגשים; אבל תחת זאת, זה תלוי בהפרש הפאזות בכל נקודת התנגשות. הפרש פאזות קטן גורר שהעוצמה של הגל המשולב גדולה יותר מאשר מה שאנו מצפים שתהיה, בעוד שהפרש פאזות גדול גורר שהעוצמה המשולבת קטנה יותר. אינטואיציה כלשהי לגבי איך זה ייתכן שהעוצמה המשולבת של הגלים תהיה גדולה יותר מהעוצמה של כל אחד בנפרד - זכרו שאנחנו מסתכלים כאן רק על נקודה אחת, אבל גלים הם לא תופעה נקודתית אלא מרחבית, ולכן שני הגלים מתנגשים בעוד שלל מקומות אחרים, עם הפרשי פאזה אחרים, ואנחנו מצפים שכמות האנרגיה הכוללת של הגלים תישמר, כך שאם העוצמה “נמוכה מדי” במקום אחד, הפיצוי יבוא בתור עוצמה “גבוהה מדי” במקום אחר.

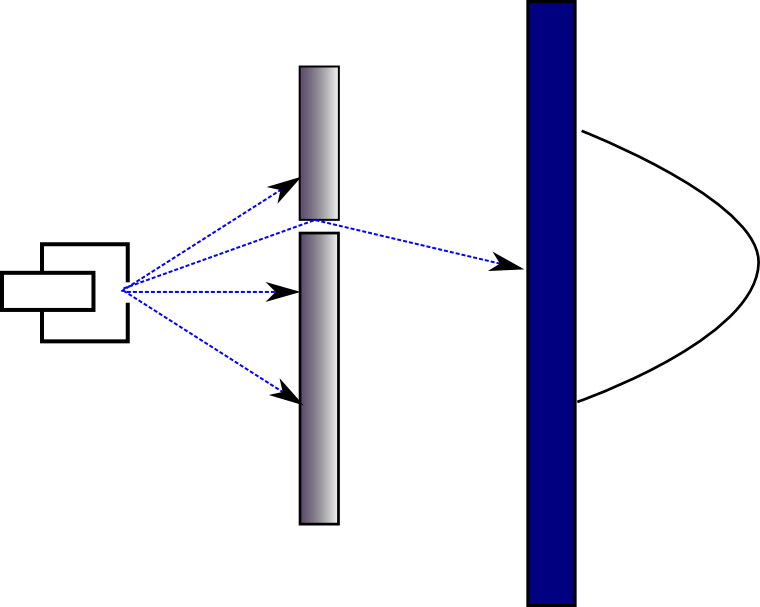
לצורה המוזרה הזו שבה גלים מתחברים יש שם: התאבכות. כעת, איך זה מתקשר לניסוי שני הסדקים שלנו? במקום רובה שיורה קליעים, אנחנו משתמשים במקור שמייצר גל שמתפזר במעגל סביב המקור, כמו אבן שזורקים לבריכה. הגל נע עד שהוא מגיע למחסום שעוצר אותו למעט בשני הסדקים. המחסום בעצם מפרק את הגל לשני גלים שונים, שכל אחד מהם יוצא מאחד מהסדקים. ככה זה נראה:

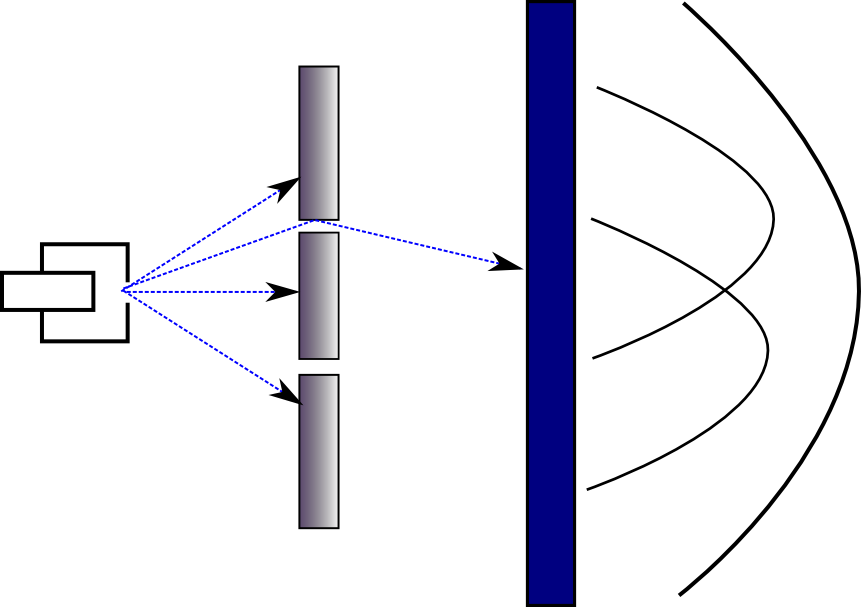
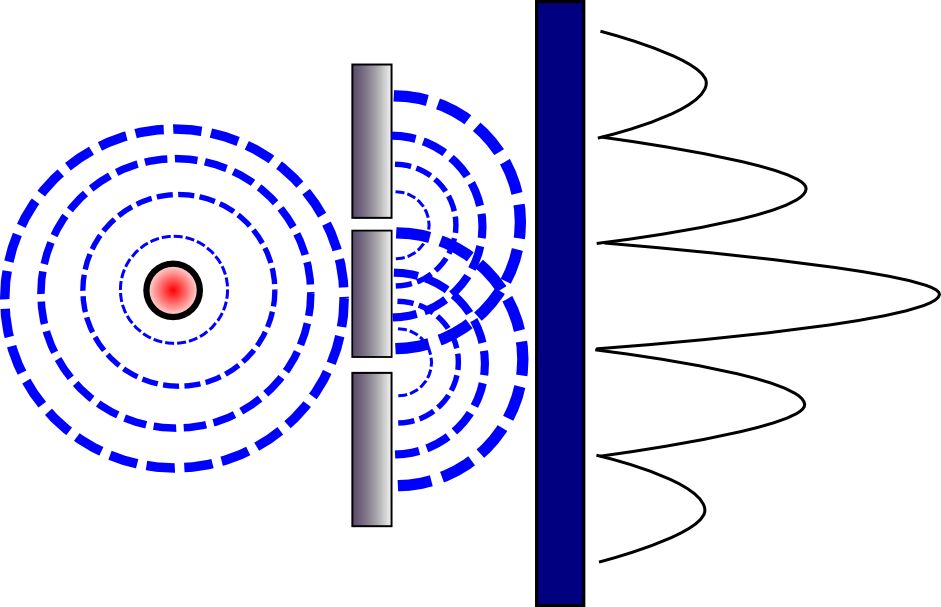
הגלאי שמצדו השני של המחסום כבר לא מודד פגיעות של קליעים, אלא את עוצמת הגל שמגיע אליו. עכשיו, אם נחסום את אחד מהסדקים ונסתכל על הגלאי, נראה שהגלאי מציג תבנית שדומה מאוד לזו של פגיעת הקליעים (עוצמת הגל נחלשת ככל שהולכים לצדדים כי ככל שהגל מתרחק, כך האנרגיה שלו מתפזרת על פני שטח גדול יותר ולכן העוצמה הנקודתית שלו נחלשת); אבל אם נפתח את שני הסדקים, נקבל משהו מופרע לגמרי:

המשהו המופרע הזה הוא בדיוק התבנית של ההתאבכות שתיארתי קודם מבחינה מתמטית - אנחנו רואים שעוצמת הגלים המתאבכים מאוד חזקה באמצע (לא במקרה; מטעמי סימטריה די ברור שהפרש הפאזות יהיה אפס) ואז נחלשת, ואז שוב מתחזקת אבל פחות, ואז שוב נחלשת וכן הלאה וכן הלאה.

איך כל זה מתקשר לקוונטים? הרעיון של פיינמן בשימוש בניסוי הזה היה פשוט מאוד. הוא אמר - הנה אנחנו רואים שני סוגים שונים של התנהגויות של יצורים פיזיקליים כשהם פוגשים שני סדקים שכאלו. כשיש לנו חלקיקים - מה שתואר על ידי ה”קליעים” - מה שקורה הוא שהחלקיקים עוברים “אחד-אחד” דרך הסדקים; שכל חלקיק עובר רק דרך סדק אחד; ושהתבנית שמתקבלת על הגלאי היא פשוטה יחסית ומהווה את סכום התבניות שנקבל על הגלאי אם נסגור את אחד הסדקים. לעומת זאת, כשיש לנו גלים אז כל גל עובר “בבת אחת” דרך שני הסדקים, מתפצל לשני גלים שונים, ואז הגלים הללו מתאבכים ויוצרים תבנית מורכבת על הגלאי, שאיננה סכום התבניות שנקבל אם נסגור את אחד מהסדקים אלא שילוב מורכב יותר שלהן.

ועכשיו פיינמן אומר - מה יקרה אם נעשה את הניסוי הזה עם “רובה” שיורה אלקטרונים, ויורה אותם “אחד אחד”?

אני אדגיש שוב שכאשר פיינמן הציע את הניסוי, לא היה ניתן לבצע ניסוי כזה בצורה מעשית; פיינמן התבסס על ניסויים אחרים שכן היה ניתן לבצע אבל היו מורכבים יותר, ולכן הוא יכל לתאר מה יקרה בניסוי הדמיוני שלו. מה שיקרה הוא הדבר המוזר הבא: אמנם, אנחנו יורים את החלקיקים “אחד אחד”, אבל על הגלאי נקבל תבנית התאבכות בכל זאת, כאילו ירינו גלים ולא חלקיקים.

זה כמובן מאוד מוזר, כי עם מי בדיוק האלקטרון הבודד “מתאבך”? הרי או שהוא עובר דרך סדק אחד, או שהוא עובר דרך הסדק השני, לא? ובכן, אפשר לומר שייתכן שבניגוד לקליעים, אלקטרונים הם יצורים מסובכים ואיכשהו אם שני הסדקים פתוחים אז האלקטרון עובר דרך אחד מהם, ואז פתאום מחליט ללכת דרך השני, ואז שוב דרך הראשון… אבל זה לא נראה סביר כל כך, כי אם סוגרים את אחד הסדקים מתקבלת על המסך תבנית “נורמלית”. ולכן מה שקורה הוא שכאשר פותחים עוד סדק, פתאום יש מקומות שהגלאי קולט בהם פחות אלקטרונים מאשר קודם. פתחנו עוד סדק, לכאורה זה אמור רק להגדיל את הסיכוי של אלקטרונים לפגוע במסך, ובפועל מספר האלקטרונים שפוגעים בנקודות מסויימות במסך קטן. איך זה אפשרי? המסקנה המתבקשת היא שאולי אלקטרון הוא גל ולא חלקיק. מצד שני, ההתנהגות של אלקטרון היא התנהגות של חלקיק - הגלאי מזהה רק פגיעה של אלקטרון יחיד בכל פעם, ותמיד באותה עוצמה. אוהבים לומר על זה לפעמים שהאלקטרון מתנהג גם כמו גל וגם כמו חלקיק, אבל בעצם הוא לא מתנהג כמו אף אחד מהם; הוא מתנהג בצורה ששני המושגים הקלאסיים של חלקיק ושל גל לא מסוגלים לתאר בצורה מלאה. משהו מוזר “קורה שם בפנים” וצריך מודל מתמטי חדש כדי לתאר אותו - מודל שיצליח איכשהו להכליל גם את ההתנהגות ה”גלית” וגם את ההתנהגות ה”חלקיקית”.

רוצים משהו עוד יותר מוזר? בבקשה. נניח שאנחנו רוצים לבדוק אם האלקטרון אכן עובר איכשהו דרך שני הסדקים. אז אנחנו שמים גלאים בכל אחד מהסדקים - גלאים שלא אמורים להסיט את האלקטרון ממסלולו בצורה משמעותית ועדיין מאפשרים לנו לדעת שהוא היה שם. התוצאה תהיה כפולה - ראשית, אנחנו נגלה שהאלקטרון אכן עובר רק דרך אחד משני הסדקים בכל פעם - הוא לא קליע הקסם מההתנקשות בקנדי - ושנית, תבנית ההתאבכות תיעלם. המדידה שביצענו, שלכאורה לא הייתה אמורה להשפיע בצורה משמעותית על מסלול האלקטרון, מחסלת לחלוטין את תופעת ההתאבכות; תחת זאת נראה על המסך תבנית דומה לזו של קליעי הרובה מההתחלה. המדידה איכשהו “ניטרלה” את התכונות הגליות של האלקטרון והותירה רק את התכונות החלקיקיות. זה שונה מאוד ממה שקורה בעולם המקרוסקופי, שבו ברוב המקרים ביצוע מדידה לא מקלקל לנו את הניסוי כי ה”נזק” שהמדידה גורמת הוא זניח (למשל, נניח שאתם מגלגלים כדור במורד מדרון משופע ותוך כדי כך אתם צופים בו - העובדה שאתם צופים בו מעידה על כך שפגע בכדור אור ואז חזר אליכם; אבל ההתנגשות הזו של קרני אור עם הכדור לא משפיעה באופן מהותי על המסלול שלו ולכן הניסוי לא מתקלקל). כאן לעומת זאת לא משנה כמה המדידה שלכם תיעשה בצורה עדינה - עצם ביצוע המדידה הורס לחלוטין את הניסוי, כל עוד המדידה לא עדינה מדי מכדי שתוכל להגיד משהו.

לא הבנתם כלום? ברוכים הבאים לתורת הקוונטים. אבל אני לא רוצה להפחיד אתכם - זה משתפר בהמשך.

הפרטים המדוייקים של הניסוי המחשבתי של פיינמן יותר מורכבים ממה שאני מתאר כאן, ואני מאוד ממליץ למי שסקרן לנסות לקרוא אותם - הוא מכסה הרבה יותר תרחשי “מה אם” ומסיק מהם עוד מסקנות (למשל, מה יקרה אם ננסה להקטין עוד ועוד את ה”נזק” שהגלאי של האלקטרונים עושה להם?) אבל לעת עתה מספיק לי עם מה שכבר תיארתי. בינתיים מה שאנחנו צריכים להבין מכל זה הוא שיש לנו תופעות טבע שפשוט לא ניתנות להסבר באמצעות המודלים הסטנדרטיים. לכן, כשיגיע מודל מתמטי פשוט שכן מתאר אותן באופן מדויק אנחנו נשמח מאוד.

כעת אני רוצה לעבור לתיאור של ניסוי שני, פשוט יותר באופיו, וכזה שניתן לתאר את מה שקורה בו גם בעזרת פיזיקה “קלאסית”. עם זאת, קל מאוד להסביר את מה שקורה בו בעזרת מודל קוונטי וזו תהיה ההזדמנות הראשונה שלנו לראות טיפה איך המתמטיקה של העסק נראית. הרעיון הוא פשוט: יש לנו מקור אור ואנחנו מקרינים אותו על מסך, ואז מכניסים פילטרים שמבוססים על הקיטוב של האור. אני לא אסביר במדויק מה זה קיטוב כרגע, אבל הרעיון לא מסובך - אינטואיטיבית, אם יש לנו גל, קיטוב הוא הכיוון שבו הגל “מתנדנד” - זאת להבדיל מהכיוון שבו הגל נע. תדמיינו רגע שאתם עפים על טיל. הכיוון שאליו הטיל עף הוא הכיוון שבו אתם נעים, אבל אתם מסוגלים להזיז את הגוף על הטיל ימינה ושמאלה ולמטה ולמעלה. תחשבו שפתאום אתם נכנסים למנהרה צרה, והדרך היחידה להבטיח שלא תעופו מהטיל היא שתטו את הגוף ימינה - זו אינטואיציה לקיטוב; ה”קיטוב” שלכם הוא ימינה. המנהרה היא מין “פילטר” שיסנן את כל מי שהטו את הגוף שמאלה במקום ימינה. ומה עם מי שלא הטו את הגוף לא שמאלה ולא ימינה? ובכן, חלקם יספיקו להטות את הגוף ימינה בזמן, וחלקם לא. ככל שהגוף הוטה יותר שמאלה, כך הסיכוי שהם יספיקו להטות את הגוף ימינה קטן יותר. אתם מבינים את הרעיון.

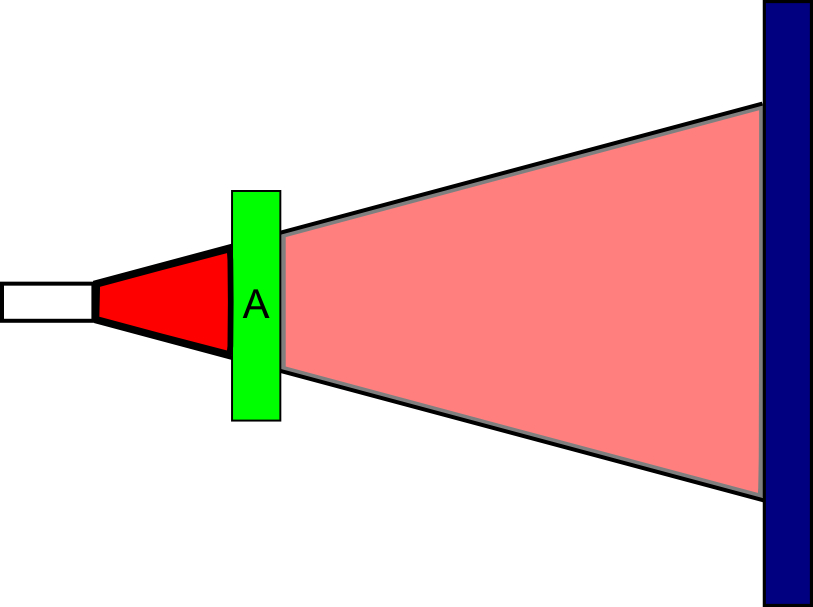
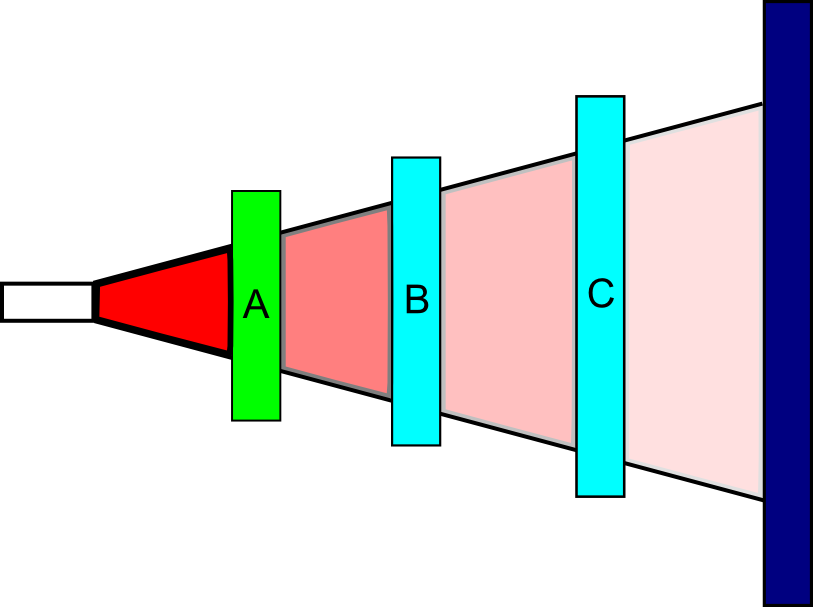
אם נשים פילטר מקטב שאקרא לו A אל מול קרן אור “רגילה”, שבה הקיטוב של הגלים שמרכיבים אותה הוא לא אחיד אלא אקראי, מה שיקרה הוא שבערך חצי מהאור יצליח לעבור את המקטב - והאור שעבר יהיה מקוטב בדיוק בזווית של המקטב. בואו נסמן ב-\( \uparrow \) את הכיוון של המקטב A הזה.

עכשיו, אחרי A נשים פילטר מקטב נוסף, C, שזווית הקיטוב שלו מאונכת לזו של A, כלומר היא \( \rightarrow \). במונחי הטיל-ומנהרה שנתתי קודם, C הוא “כיוון שמאל” אם A הוא “כיוון ימין” - כל מי שכבר מקוטב בזווית של \( \uparrow \) ואז נתקל בקיטוב של \( \rightarrow \) לא יצליח לעבור. התוצאה? אחרי ששמנו את C בהמשך של A לא נראה שום דבר על המסך.

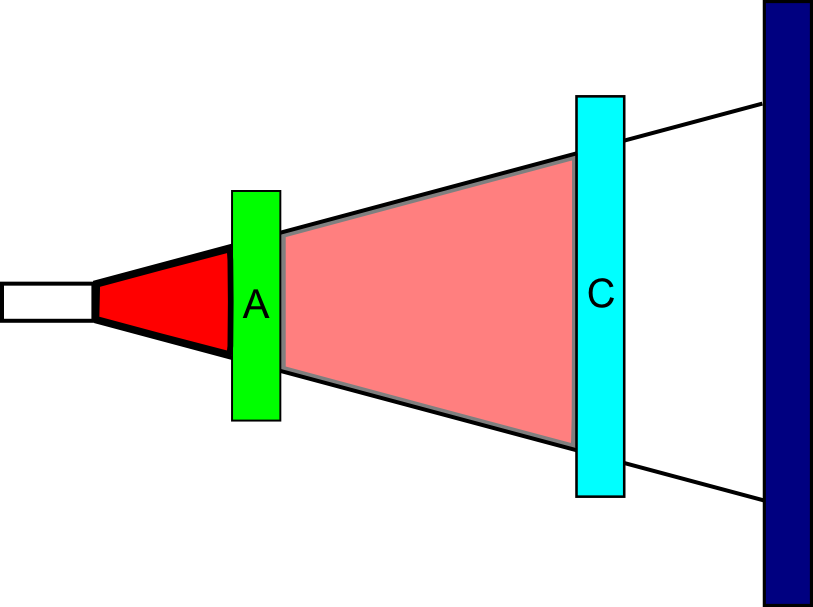
עד כאן, הגיוני. עכשיו ניקח פילטר B שזווית הקיטוב שלו היא ב-45 מעלות הן ל-A והן ל-C; נסמן אותה \( \nearrow \) אם נשים את B בין A ו-C, המצב ישתנה - פתאום כן נראה אור על המסך, בערך ב-\( \frac{1}{8} \) העוצמה של האור המקורי. כלומר - הוספה של עוד פילטר בין שני הקיימים דווקא הגבירה את עוצמת האור. מה קורה כאן?

ובכן, אם חושבים על האור בתור גל, זה לא כל כך מפתיע; כבר ראינו שמקטב יודע לשנות את הקיטוב של גל שנכנס אליו, תוך “מחיר” של אובדן חלק מהעוצמה שלו (הזווית בין הקיטוב של האור הנכנס ובין הקיטוב של המקטב קובעת כמה מהעוצמה תאבד). אז B משנה את הקיטוב של האור שיצא מ-A בצורה כזו שמעבר דרך C לא יהיה יותר הרסני. את כל זה אפשר להסביר כבר עם פיזיקה “קלאסית”, כאמור. אלא שאור לא באמת מציית באופן מוחלט לחוקי הפיזיקה הקלאסית; יש סיטואציות שבהן האור מתנהג כמו חלקיק ולא כמו גל (למשל, האפקט הפוטואלקטרי, אם אתם רוצים לגגל), ולכן מדברים על חלקיקים יסודיים של האור - פוטונים. בדומה לאלקטרונים, כך גם פוטונים מפגינים התנהגות של חלקיק בסיטואציות מסויימות ושל גל בסיטואציות אחרות, והמידול ה”כללי” שלהם נעשה במסגרת המתמטיקה של תורת הקוונטים. אז בואו ונראה סוף סוף את המידול הזה בהקשר של קיטוב, ונראה איך הוא מסביר את הניסוי שלנו בצורה מאוד פשוטה.

הבה ונתבונן על פוטון בודד. בהתחלה, כשהוא רק יוצא ממקור האור, אנחנו לא יודעים מה הקיטוב שלו; כל מה שאנחנו יודעים הוא שהקיטוב נמצא בסופרפוזיציה של מצבי קיטוב בסיסיים. באופן פורמלי-מתמטי, אנחנו חושבים על הקיטוב של הפוטון בתור איבר במרחב וקטורי דו-ממדי מעל \( \mathbb{C} \), שיש לו בסיס אורתונורמלי שאנו מסמנים את איבריו בתור \( \left|\uparrow\right\rangle \) ו-\( \left|\rightarrow\right\rangle \). הסיבה ל-\( \left|\cdot\right\rangle \) המוזר שבו אנחנו שמים את החצים תתברר בפוסט הבא כשנתחיל לדבר יותר על הפורמליזם; כרגע זה סתם סימון מוזר (שהוא הסימון הסטנדרטי כשמתעסקים בתורת הקוונטים, לטוב ולרע). דרישה אחת שיש לנו על הקיטוב והצורך בה יתברר עוד רגע היא שהנורמה שלו תהיה 1. המשמעות היא שהקיטוב של הפוטון ניתן להצגה בתור \( a\left|\uparrow\right\rangle +b\left|\rightarrow\right\rangle \) כאשר \( a,b\in\mathbb{C} \) ומקיימים \( \left|a\right|^{2}+\left|b\right|^{2}=1 \).

כעת, מה קורה כאשר הפוטון עובר דרך הפילטר A? מה שקורה הוא שהפילטר מקיים אינטראקציה (“מדידה”) עם הפוטון, שמשנה (“מקריסה”) את המצב הקוונטי שלו; הפילטר מכריח את המצב הקוונטי להפוך להיות או \( \left|\uparrow\right\rangle \) (מה שפורמלית אפשר לכתוב בתור \( 1\cdot\left|\uparrow\right\rangle +0\cdot\left|\rightarrow\right\rangle \)) או \( \left|\rightarrow\right\rangle \). במקרה הראשון הפוטון יצליח לעבור את הפילטר, ובמקרה השני הפוטון יוחזר על ידי הפילטר. כעת, איך נקבע מי משתי האפשרויות תתרחש בפועל? התשובה היא שזה נקבע באקראי, כשההסתברות נקבעת מתוך מקדמי הסופרפוזיציה: אם הפוטון היה במצב \( a\left|\uparrow\right\rangle +b\left|\rightarrow\right\rangle \) אז ההסתברות שהוא יעבור ל-\( \left|\uparrow\right\rangle \) היא \( \left|a\right|^{2} \) וההסתברות שהוא יעבור ל-\( \left|\rightarrow\right\rangle \) היא \( \left|b\right|^{2} \). זו הסיבה לדרישה \( \left|a\right|^{2}+\left|b\right|^{2}=1 \) - אנחנו רוצים לקבל הסתברות תקינה (כלומר, שסכום כל האפשרויות הוא בדיוק 1).

“רגע רגע רגע”, אתם בוודאי אומרים. “אתה זורק עלינו כל מני דרישות וכל מני טענות - הקיטוב הוא איבר במרחב וקטורי, וההסתברויות הן ערך מוחלט בריבוע ועוד דברים מוזרים. מאיפה לך? מה המצאת את זה פתאום?”. ובכן, כזכור, תורת הקוונטים היא מודל מתמטי. לקח לאנשים זמן לפתח את המודל המתמטי שאני מתאר כרגע, והם עשו זאת על בסיס תצפיות וניסויים, והמודל עצמו מוכיח את עצמו בכך שהוא אכן מתאים לתוצאות הניסויים. לכן אני צריך לבקש מכם פשוט לקבל את המודל כמות שהוא - הוא עובד, וזה די מופלא שהוא עובד.

אם אנחנו מניחים פילוג אחיד על הסופרפוזיציות האפשריות של הפוטונים שיוצאים ממקור האור, אז שיקולי סימטריה מראים לנו שפוטון אקראי יעבור את A בהסתברות \( \frac{1}{2} \). לא מאמינים ל”שיקולי סימטריה”? אין בעיה - תחשבו בעצמכם! זה תרגיל לא קשה בהסתברות רציפה. עכשיו, נניח שהפוטון מגיע ישר אל הפילטר C, מה קורה עכשיו? מה שקורה הוא ש-C מבצע בדיוק את אותה המדידה ש-A מבצע, אבל הוא מעביר רק את הפוטונים שלאחר המדידה קרסו למצב \( \left|\rightarrow\right\rangle \). אם הגיע אל C פוטון שהמצב הקוונטי שלו הוא \( 1\cdot\left|\uparrow\right\rangle +0\cdot\left|\rightarrow\right\rangle \), הרי שההסתברות שהפוטון יקרוס לאחר המדידה אל המצב \( \left|\rightarrow\right\rangle \) היא \( \left|0\right|^{2}=0 \), ולכן אף פוטון לא יעבור את C.

כעת, מה קורה אם שמים את B באמצע? מה ש-B מבצע הוא מדידה מעניינת; זו מדידה ביחס לבסיס אורתונורמלי שונה לאותו מרחב וקטורי. מה ש-B יעשה הוא קודם כל לייצג את המצב הקוונטי של הפוטון שהגיע אליו באמצעות הבסיס האורתונורמלי החדש, ואז יקריס אותו לאחד משני מצבי הבסיס הללו על פי החוקים שכבר ראינו. את הבסיס של B אסמן ב-\( \left|\nearrow\right\rangle \) ו-\( \left|\searrow\right\rangle \); את שני הוקטורים הללו ניתן לייצג בעזרת אברי הבסיס המקורי באמצעות הזהויות הבאות: \( \left|\nearrow\right\rangle =\frac{\left|\uparrow\right\rangle +\left|\rightarrow\right\rangle }{\sqrt{2}} \) ו-\( \left|\searrow\right\rangle =\frac{\left|\uparrow\right\rangle -\left|\rightarrow\right\rangle }{\sqrt{2}} \). כאן החלוקה היא בשורש 2 כדי שנקבל עדיין בסיס אורתונורמלי (כלומר, שהנורמה של האיברים תהיה 1). שוב, אתם יכולים לשאול מאיפה לי לדעת ש-\( \left|\nearrow\right\rangle \) הוא בדיוק הצירוף הלינארי שתיארתי לעיל - אני יכול לנפנף אתכם או סתם לומר שככה אני מגדיר את \( \left|\nearrow\right\rangle \) ואז האתגר הוא רק למצוא מקטב שמתאים ל-\( \left|\nearrow\right\rangle \) במציאות.

כעת, אם הגיע פוטון עם קיטוב \( \left|\uparrow\right\rangle \) מ-A אל המקטב B, בואו ונראה איך תתנהל המדידה. ראשית המקטב מציג את \( \left|\uparrow\right\rangle \) בעזרת הבסיס האורתונורמלי שלו, כלומר

\( \left|\uparrow\right\rangle =\frac{1}{2}\left[\left(\left|\uparrow\right\rangle +\left|\rightarrow\right\rangle \right)+\left(\left|\uparrow\right\rangle -\left|\rightarrow\right\rangle \right)\right]=\frac{\sqrt{2}}{2}\left(\frac{\left|\uparrow\right\rangle +\left|\rightarrow\right\rangle }{\sqrt{2}}+\frac{\left|\uparrow\right\rangle -\left|\rightarrow\right\rangle }{\sqrt{2}}\right)=\frac{\sqrt{2}}{2}\left|\nearrow\right\rangle +\frac{\sqrt{2}}{2}\left|\searrow\right\rangle \)

ולכן ההסתברות של הפוטון לקרוס ל-\( \left|\nearrow\right\rangle \) היא \( \left(\frac{\sqrt{2}}{2}\right)^{2}=\frac{2}{4}=\frac{1}{2} \). במילים אחרות, חצי מהפוטונים שמגיעים ל-B יעברו את B, ולאחר מכן הם יהיו במצב הקוונטי \( \left|\nearrow\right\rangle \). חישוב דומה מראה שאחרי הגעה ל-C חצי מהפוטונים (שהגיעו ל-C עם קיטוב \( \left|\nearrow\right\rangle \)) יעברו את C. סה”כ קיבלנו שחצי-של-חצי-של-חצי מהפוטונים שיצאו ממקור האור מגיעים אל הגלאי שאחרי שלושת המקטבים, כלומר עוצמת האור תהיה שמינית מהעוצמה המקורית שלו, כצפוי.

לסיום בואו נחזור לניסוי שני הסדקים. גם כשאנחנו חמושים בתורת הקוונטים זה לא אומר שיהיה קל לבנות מודל שמתאר ספציפית את ניסוי שני הסדקים, ובכלל לא הצגתי עד כה את המושג המרכזי שבו אנחנו משתמשים בבניית מודלים שכאלו - - משוואת שרדינגר. לכן אסתפק בנפנוף ידיים שמטרתו להסביר את רוח הדברים אבל הוא ממש ממש לא פתרון פורמלי. בואו נסתכל על נקודה כלשהי בגלאי. כעת, נניח שרק סדק מס’ 1 פתוח ונסתכל על הייצוג הקוונטי של המצב של החלקיק שעובר דרך סדק 1 ומגיע למסך. הייצוג הזה הוא צירוף לינארי של וקטורים שמייצגים נקודות שונות על המסך (“צירוף לינארי” הוא שקר בפני עצמו, כי הסיטואציה הכללית יותר סבוכה, אבל כבר אמרתי שאני לא הולך לדייק כאן). נסמן ב-\( a_{1} \) את המקדם של הוקטור שמייצג את הנקודה במסך שאנו בוחנים. אז ההסתברות שהחלקיק יימדד בנקודה הזו היא \( \left|a_{1}\right|^{2} \). בדומה נסמן ב-\( a_{2} \) את המקדם של הוקטור שמייצג את הנקודה במסך במקרה שבו רק סדק 2 פתוח. כעת, נניח ששני הסדקים פתוחים; מה שיקרה הוא שהמקדם של הוקטור יהיה סכום המקדמים \( a_{1}+a_{2} \), ולכן ההסתברות לפגוע בנקודה הזו בגלאי אם שני הסדקים פתוחים היא \( \left|a_{1}+a_{2}\right|^{2} \). עכשיו, שימו לב שבאופן כללי \( \left|a_{1}+a_{2}\right|^{2}\ne\left|a_{1}\right|^{2}+\left|a_{2}\right|^{2} \). יותר מכך - \( \left|a_{1}+a_{2}\right|^{2} \) הוא בדיוק הכפל של \( a_{1}+a_{2} \) בצמוד המרוכב שלו, בדיוק כמו חישובי העוצמות במקרה שבו דיברנו על התאבכות של גלי מים. מכאן אנו מגיעים לאותה תוצאה - אבל העיקר פה הוא להבין איך נראים המקדמים \( a_{1},a_{2} \) ועל זה אני לא הולך לדבר כרגע.

בפוסט הבא אפסיק לנסות לדבר על פיזיקה ואחזור לדבר על מתמטיקה; ספציפית, על המודל המתמטי היחסית אבסטרקטי שבו משתמשים בתורת הקוונטים ויהיה שימושי עבורנו כשנדבר על חישובים קוונטיים.