אלגוריתם גרובר

אלגוריתם גרובר הוא הדוגמה הראשונה שכדאי להראות כשמתחילים להראות אלגוריתמים בחישוב קוונטי, מכיוון שהוא פשוט יחסית, עובד בצורה מאוד אינטואיטיבית וציורית, ויש לו יתרון מוכח על אלגוריתמים קלאסיים שפותרים את אותה הבעיה. ומה הבעיה הזו? בעיה של חיפוש במבנה נתונים לא מסודר.

ברוב מבני הנתונים בעולם יש סדר וארגון כלשהם שמאפשרים לנו לחפש בהם איברים בצורה נוחה. דוגמה קלאסית היא מערך ממויין - במערך כזה, שבו אפשר להשוות כל זוג איברים והם ממויינים מהקטן אל הגדול, אפשר למצוא איבר בזמן \( \log N \) כאשר \( N \) הוא מספר האיברים הכולל במערך, באמצעות חיפוש בינארי. אבל מה קורה במערך בלי שום סדר וארגון? אין לנו ברירה אלא לבצע \( N \) שאילתות - לעבור איבר איבר ולבדוק אם הוא מתאים לקריטריון החיפוש שלנו. כלומר, זמן הריצה שלנו הוא \( O\left(N\right) \) האלגוריתם של גרובר פותר את הבעיה בזמן ריצה שהוא \( O\left(\sqrt{N}\right) \) - כלומר, יש לאלגוריתם זמן ריצה טוב יותר אסימפטוטית מהאלגוריתם הקלאסי הטוב ביותר שיכול להיות. זו המחשה ליתרון אמיתי של חישוב קוונטי על פני חישוב רגיל.

איך קורה הקסם הזה? איך אלגוריתם קוונטי מחפש במבנה נתונים לא מסודר כל כך מהר? התשובה היא שבדיוק כפי שמתואר חישוב קוונטי בספרי מדע פופולרי: האלגוריתם איכשהו מריץ את השאילתה “האם אתה האיבר שאני מחפש?” על כל אברי המערך בו זמנית, באמצעות הסתמכות על העובדה שהוא מחזיק מעין סופרפוזיציה של כל אברי המערך. אבל לעשות את זה, זה עדיין לא מספיק טוב - מדידה של הסופרפוזיציה הזו תניב את האיבר שאנחנו מחפשים רק בהסתברות נמוכה. לכן גרובר מבצע תהליך של הגברה - מניפולציה של המצב הקוונטי שחוזרת על עצמה שוב ושוב, ומבטיחה שאם האיבר שאנחנו מחפשים בכלל קיים במערך, אז לאט לאט ההסתברות שמדידה תחזיר אותו הולכת וגדלה. מספיק לחזור על התהליך הזה \( O\left(\sqrt{N}\right) \) פעמים כדי לקבל הסתברות מצויינת למצוא את האיבר שאנחנו מחפשים.

בפוסט המבוא שלי לנושא החישוב הקוונטי אמרתי ש”עדיין אין לנו הוכחה מתמטית שחישוב קוונטי הוא אכן חזק מבחינת סיבוכיות יותר מחישוב רגיל”, מה שלכאורה נסתר על ידי האלגוריתם של גרובר, ולכן צריך להבהיר את הכוונה ב”חזק מבחינת סיבוכיות”. בואו נדבר למשל על מכונות טיורינג - המודל הפשוט ביותר הוא חד סרטי אבל יש גם מודל דו סרטי ועוד שלל וריאציות. ההבדלים בין המודלים הללו מוסיפים כוח חישובי כלשהו; יש בעיות שהמודל הדו סרטי יפתור בזמן \( T \) אך למודל החד סרטי יידרש זמן \( T^{2} \) כדי לפתור, כלומר המודל הדו סרטי פותר את הבעיה בזמן ריצה שורש של זמן הריצה שנדרש למודל החד סרטי, בדיוק כמו השיפור של אלגוריתם גרובר.

ההבדלים הללו יכולים להיות חשובים בחיים האמיתיים, אבל בחיים האמיתיים יש אינסוף פרטי מימוש אחר שצריכים לדבר עליהם - מה שפותרים איתו בעיות הוא מחשב, ולא מכונת טיורינג, והמחשב מתבסס על מעבד, ובמעבד יש אופטימיזציות, ויש סט מורכב של פקודות לוגיות. ויש ענייני תזמון וניהול אנרגיה, ויש מטמון (Cache), ויש הרצת פקודות שלא על פי הסדר המתואר בתוכנית, ויש ניבוי של קפיצות בפקודות if ויש עוד אינסוף דברים שכולם קריטיים לחלוטין עבור תכנות בחיים האמיתיים. ואני לא רוצה שיתקבל רושם שגוי - אלו דברים ממש מגניבים, ובהחלט מתחשבים בהם במציאות. אבל כשאנחנו מתעסקים בסיבוכיות, כדי לא לטבוע בפרטים כאלו, אנחנו מנסים להתרחק מהכל ולדבר בצורה “נקיה” ככל האפשר.

ומכיוון שהמודל הדו סרטי והמודל החד סרטי שונים זה מזה מבחינת הסיבוכיות שלהם, אנחנו מאמצים רזולוציה שבה הם נראים אותו דבר. זה מה שמוביל להגדרה של “חישוב יעיל” ככזה שמתבצע בזמן פולינומי, ולהגדרת מחלקת הסיבוכיות \( \mbox{P} \). גם הגדרת מחלקת הסיבוכיות של חישוב קוונטי יעיל, BQP, הונעה משיקולים דומים. מה שאמרתי בפוסט הראשון הוא שאין לנו הוכחה מתמטית לכך ש-\( \mbox{P}\ne\mbox{BQP} \) (הוכחה שכזו תהיה, למשל, הוכחה לכך שפירוק לגורמים לא ניתן לביצוע בזמן פולינומי; זאת מכיוון שנראה בהמשך את אלגוריתם שור שהוא אלגוריתם קוונטי יעיל לפירוק לגורמים). האלגוריתם של גרובר לא מהווה שיפור בסדר גודל מספיק כדי שיהיו לו השלכות של ממש על שאלת \( \mbox{P}\ne\mbox{BQP} \) המדוברת. אגב, באותה פסקה בפוסט המבוא אמרתי גם “יש דברים שאפשר להוכיח שבהם חישוב קוונטי עוזר לנו יותר מאשר בחישוב רגיל ואציג דוגמה אחת לפחות בפוסטים הבאים” - האלגוריתם של גרובר הוא בדיוק דוגמה שכזו.

בואו נעבור לניסוח קצת יותר פורמלי של הבעיה. אני מתאר את הבעיה בתור “חיפוש במסד נתונים”, אבל אנחנו מעדיפים לשמור את “מסד הנתונים” הזה אבסטרקטי ככל הניתן כדי שהאלגוריתם לא יהיה תלוי בפרטים הטכניים שלו. האופן שבו אוהבים בתורת הסיבוכיות לבצע אבסטרקציות כאלו היא בעזרת אורקל. אורקל הוא פרוצדורה חישובית כלשהי שאנחנו מתייחסים אליה כאל “קופסה שחורה” - לא יודעים איך היא ממומשת, ומניחים שזמן הריצה שלה הוא זניח. האלגוריתם שלנו ימדד, בין היתר, על בסיס השאלה “כמה קריאות לאורקל ביצעת?”

במקרה שלנו אנחנו רוצים לייצג את אברי מסד הנתונים פשוט בתור מספרים מ-1 עד \( N \), והאורקל יקבל כקלט מספר ויגיד האם המספר הזה הוא האיבר שאנחנו מחפשים. הנה דרך לפרמל את זה: נניח כי \( N=2^{n} \) עבור מספר טבעי \( n \) כלשהו, ונייצג כל איבר במסד הנתונים באמצעות סדרה של \( n \) ביטים (אז פורמלית אנחנו מתארים פה את המספרים מ-0 עד \( N-1 \)). האורקל במקרה הנוכחי יהיה אופרטור קוונטי \( O \), שלא מבצע מדידה אבל עושה את הדבר הבא: אם \( \left|x\right\rangle \) הוא מצב קוונטי שאינו מייצג את האיבר שאנו מחפשים, אז \( \left|x\right\rangle \mapsto\left|x\right\rangle \), ואם הוא כן מייצג את האיבר שאנו מחפשים, אז \( \left|x\right\rangle \mapsto-\left|x\right\rangle \). פורמלית אפשר לדבר על פונקציה \( f\left(x\right) \) שמחזירה 1 על איברים שמתאימים לקריטריון החיפוש שלנו ו-0 אחרת, ואז \( \left|x\right\rangle \mapsto\left(-1\right)^{f\left(x\right)}\left|x\right\rangle \) הוא האופרטור.נחזור בסוף הפוסט לשאלה איך אפר להניח שיש לנו אורקל שמבצע כזה חישוב, אבל נעזוב את זה לבינתיים - העיקר הוא שיש לנו אינדיקטור כלשהו שמצביע על האיבר ה”נכון”.

האלגוריתם מתחיל כשאנחנו נמצאים במצב של סופרפוזיציה סימטרית של כל המצבים האפשריים. אבל אין צורך להניח שזה המצב ההתחלתי; אפשר להגיד שהמצב ההתחלתי הוא \( \left|00\dots0\right\rangle \) ושאנחנו עוברים למצב הסופרפוזיציה הסימטרית על ידי הפעלה של האופרטור \( H\otimes H\otimes\dots\otimes H \). כזכור, \( H \) הוא שער קוונטי שפועל על קיוביט בודד באופן הבא: \( \left|0\right\rangle \mapsto\frac{\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}} \) ו-\( \left|1\right\rangle \mapsto\frac{\left|0\right\rangle -\left|1\right\rangle }{\sqrt{2}} \). כעת, \( H\otimes H\otimes\dots\otimes H \) הוא אופרטור שפועל על כל \( n \) הקיוביטים של הרגיסטר הקוונטי שלנו; בפוסט הקודם לא הרשיתי משהו כזה אלא דרשתי ששער קוונטי יפעל על שלושה קיוביטים לכל היותר. האפקט הזה מושג על ידי שרשור \( n \) עותקים של \( H \), שכל אחד פועל על קיוביט אחר (כלומר, בעצם אני מפעיל סדרתית את \( H\otimes I\otimes\dots\otimes I \) ואז \( I\otimes H\otimes\dots\otimes I \) וכן הלאה). בהמשך אני אניח שהעניין הזה ברור לכם וכשאציין אופרטור שפועל על כל הקיוביטים “בבת אחת” נבין שמדובר על שרשור של כמה שערים (למרות שאולי לא תמיד ברור איך להציג את האופרטור כשרשור כזה). מכיוון שזה מסורבל לכתוב \( H\otimes H\otimes\dots\otimes H \) אני אשתמש בסימון \( H^{\otimes n} \) שהוא למען האמת אינפורמטיבי יותר כי \( n \) מופיע בו במפורש.

כעת, בואו נסמן \( \left|\psi\right\rangle =H^{\otimes n}\left|0\dots0\right\rangle =\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}\left|x\right\rangle \). בעזרת \( \left|\psi\right\rangle \) אפשר להגדיר אופרטור חדש: \( 2\left|\psi\right\rangle \left\langle \psi\right|-I \). האם אפשר לממש את האופרטור הזה עם שערים קוונטיים? כן, ונדבר על זה בהמשך. עכשיו אפשר לשרשר את האופרטור הזה לאופרטור \( O \) של האורקל, ולקבל אופרטור \( G=\left(2\left|\psi\right\rangle \left\langle \psi\right|-I\right)O \). עכשיו סוף סוף אפשר לתאר פורמלית את האלגוריתם של גרובר:

1. התחילו עם הרגיסטר \( R=\left|0\dots0\right\rangle \).
2. חשבו את \( R\leftarrow H^{\otimes n}R \).
3. בצעו במשך \( \sqrt{N} \) פעמים:
   1. \( R\leftarrow G\left(R\right) \)
4. מדדו את \( R \) והחזירו את התוצאה.

וזהו. בהסתברות טובה המדידה תיתן לנו \( x \) כך ש-\( f\left(x\right)=1 \). זה נראה כמו קסם, כמובן; עיקר הפוסט יוקדש לשאלה למה הקסם הזה עובד, אם כי את האינטואיציה כבר הסברתי.

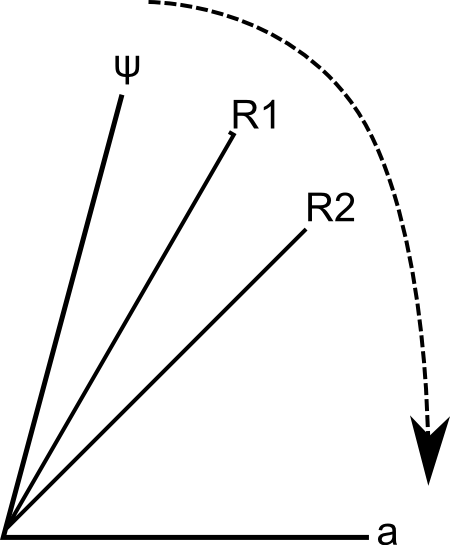
אפשר להתחיל לנתח אלגברית את \( G \), אבל הדרך המקובלת לנתח אותי היא בצורה גאומטרית. אני איום ונורא בגאומטריה ועדיין הצלחתי להבין את הרעיון הזה, אז בואו ותשתפו איתי פעולה. בואו נניח לצורך פשטות שקיים רק \( a \) יחיד כך ש-\( f\left(a\right)=1 \). נסתכל על הוקטורים \(  \left|\psi\right\rangle \) ו-\( \left|a\right\rangle \) - כנראה יעזור לכם לדמיין אותם במרחב כך ש-\( \left|a\right\rangle \) שוכב על הרצפה, ואילו \( \left|\psi\right\rangle \) נמצא בזווית כלשהי מעליו. בהתחלה \( R \) שלנו זהה ל-\( \left|\psi\right\rangle \). הרעיון הוא שבכל הפעלה של \( G \), \( R \) הולך “להימשך” לכיוון \( \left|a\right\rangle \) שעל הרצפה. אני גרוע בציורים תלת ממדיים אז הנה איור דו ממדי של “מבט מהצד” על מה שקורה:

אם כן, כל הפעלה של \( G \) מסובבת את \( R \) קצת בתוך המישור שנפרש על ידי \( \left|\psi\right\rangle \) ו-\( \left|a\right\rangle \). נסובב מספיק, ו-\( R \) יהיה קרוב ל-\( \left|a\right\rangle \) כך שמדידה של \( R \) תניב את \( \left|a\right\rangle \) בהסתברות טובה. נסובב יותר מדי - ו-\( R \) יחלוף על פני \( \left|a\right\rangle \) ויתחיל להתרחק ממנו, אז לסובב יותר מדי זה גם כן לא רעיון טוב.

בואו ננסה עכשיו להיות קצת יותר פורמליים. אני רוצה לדבר על גאומטריה וזוויות וכאלה. במרחבי מכפלה פנימית נהוג להגדיר זווית באמצעות המכפלה הפנימית: אם \( a,b \) הם וקטורים, אז מאי שוויון קושי שוורץ נובע ש-\( \left|\left\langle a,b\right\rangle \right|\le\|a\|\|b\| \). זה אומר ש-\( 0\le\frac{\left|\left\langle a,b\right\rangle \right|}{\|a\|\|b\|}\le1 \) ולכן יש למשוואה \( \cos\alpha=\frac{\left|\left\langle a,b\right\rangle \right|}{\|a\|\|b\|} \) פתרון יחיד עם \( \alpha\in\left[0,\frac{\pi}{2}\right] \). ה-\( \alpha \) הזו מוגדרת להיות הזווית בין \( a,b \). כדי שיתקבל \( \alpha=\frac{\pi}{2} \) צריך שיתקיים \( \left|\left\langle a,b\right\rangle \right|=0 \), כלומר ש-\( a,b \) יהיו אורתוגונליים.

כעת, מהו \( \left|\left\langle a,\psi\right\rangle \right| \)? ובכן, זה קל. \( \left|\psi\right\rangle =\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}\left|x\right\rangle \) ו-\( \left|a\right\rangle \) הוא אחד מהאיברים בצירוף הלינארי הזה. מכיוון שהצירוף הזה הוא של בסיס אורתונורמלי, נקבל ש-\( \left|\left\langle a,\psi\right\rangle \right|=\frac{1}{\sqrt{N}} \). זה מספר חיובי, ולכן \( \alpha\ne\frac{\pi}{2} \), ומכאן שניתן לכתוב את \( \alpha \) כך: \( \alpha=\frac{\pi}{2}-\theta \) כאשר \( \theta \) היא זווית חיובית.

למה לטרוח כל כך עם הסימון המסורבל הזה? מכיוון ש-\( \theta \) מאפשרת לנו לדבר במדויק על “כמה סיבוב” מבצעת \( G \) - בכל פעם שבה היא מופעלת, היא מקטינה את הזווית ב-\( 2\theta \). כלומר, אם הזווית בין \( R \) ובין \( \left|a\right\rangle \) הייתה \( \beta \) בשלב מסויים של האלגוריתם, אז אחרי הפעלת \( G \) הזווית תהיה \( \beta-2\theta \). זה אומר שאחרי \( k \) הפעלות של האלגוריתם נהיה בזווית \( \frac{\pi}{2}-\left(2k+1\right)\theta \). נניח שהיעד שלנו הוא להגיע לזווית \( \frac{\pi}{4} \), אז אנחנו רוצים שיתקיים \( \frac{\pi}{2}-\left(2k+1\right)\theta=\frac{\pi}{4} \), כלומר \( 2k+1=\frac{\pi}{4\theta} \), כלומר \( k=\frac{\pi}{8\theta}=O\left(\frac{1}{\theta}\right) \). זווית \( \frac{\pi}{4} \) היא מספיק טובה לנו, כי פירושה הוא שהמכפלה הפנימית היא לפחות \( \frac{1}{2} \), ולכן ההסתברות לקבל את \( a \) היא לפחות \( \frac{1}{4} \), וזה מספיק טוב לנו (זה אומר שבתוחלת, נזדקק לארבע הפעלות של האלגוריתם כדי להשיג את הפתרון, וזה מצויין).

איך ה-\( O\left(\frac{1}{\theta}\right) \) מתבטא בפרמטרים של הבעיה? הפרמטר שלנו הוא \( N \); מה הקשר ביניהם? אנחנו יודעים ש-\( \cos\alpha=\frac{1}{\sqrt{N}} \), ואנחנו מכירים את הזהות הטריגונומטרית \( \cos\left(\frac{\pi}{2}-x\right)=\sin x \), כלומר \( \cos\alpha=\sin\theta \) ולכן \( \theta\ge\sin\theta=\frac{1}{\sqrt{N}} \). מכאן ש-\( \frac{1}{\theta}\le\sqrt{N} \) ולכן מספר ההפעלות של האלגוריתם שנדרשות לנו הוא אכן \( O\left(\sqrt{N}\right) \) המובטח.

רק מה, עדיין לא הבנו למה \( G \) מסובב את הוקטור בכל פעם בעוד \( 2\theta \) אל עבר \( \left|a\right\rangle \). כאן האינטואיציה הגאומטרית נכנסת לתמונה במלוא כוחה: הרעיון הוא שאת פעולת הסיבוב הזו ניתן להציג בתור הרכבה של שתי פעולות שיקוף. קצת קשה (לטעמי) להרגיש אינטואיטיבית איך קורה הקסם הזה ששתי פעולות שיקוף שמבוצעות בזו אחר זו שקולות לפעולת סיבוב; כנראה הכי טוב שתעשו ניסויים בעצמכם כדי לקבל תחושה. אינטואיציה כלשהי אפשר בכל זאת לקבל מכך שהאיזומטריות היחידות במרחב הן סיבובים, שיקופים והזזות, ואם משקפים ביחס לראשית הצירים ראשית הצירים משתמרת (כך שאי אפשר לקבל הזזה) ושיקוף-של-שיקוף לא יכול להיות שיקוף בעצמו כי השיקוף השני “מתקן” את ההיפוך (כמו במראה) שהשיקוף הראשון יוצר. אז אנחנו חייבים לקבל סיבוב.

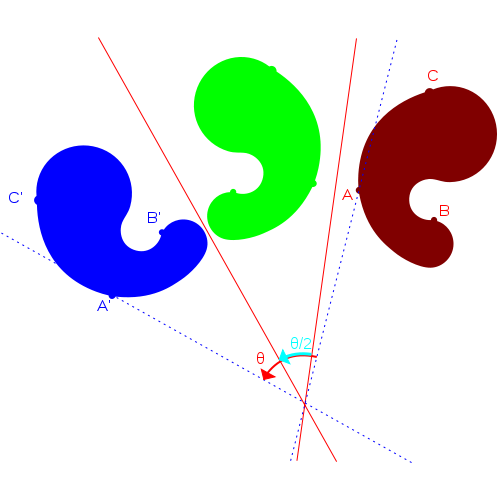
עוד אינטואיציה אפשר לקבל על ידי תמונה, באדיבות ויקיפדיה האנגלית:

בואו ניזכר לרגע איך אפשר לתאר שיקוף, פורמלית, ואז גם יהיה לנו קל לראות למה הכל יוצא כמו שאנחנו רוצים. ראשית, אני ארצה לדבר ספציפית על תיאור של שיקוף במישור, כלומר במרחב וקטורי ממימד 2. ה”בעיה” היא שהמרחב שלנו הוא ממימד \( N \), אז מה עושים? מצטמצים לתת-מרחב: זה שנפרש על ידי \( \left|a\right\rangle \) ו-\( \left|\psi\right\rangle \) (הוקטור שאנחנו מחפשים והוקטור שמתאר סופרפוזיציה אחידה). בהמשך כל הוקטורים שאדבר עליהם יהיו שייכים לתת המרחב הזה.

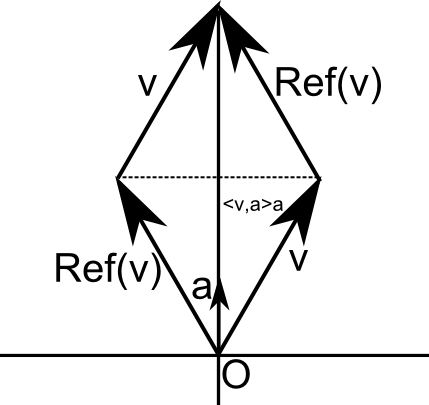
כעת בואו נדבר על שיקוף במישור. שיקוף (כפי שאפשר לראות בתמונה) הוא תמיד ביחס לציר כלשהו. לוקחים נקודה. מעבירים אנך ממנה אל הציר, ואז ממשיכים את האנך הזה לצד השני באותו האורך - תוצאת השיקוף היא הנקודה שבקצה האנך הזה. אבל יש עוד דרך לחשוב על הפעולה הזו: ראשית, אל תחשבו על “נקודה” אלא על וקטור (כלומר, קו שמחבר את ראשית הצירים עם הנקודה); שנית, קחו את הוקטור ותחברו אליו את השיקוף שלו (תדביקו את הוקטור של השיקוף הזה על הנקודה) ותחברו אל השיקוף את הוקטור - תקבלו מעוין. אחד האלכסונים של המעוין הוא הישר שדרכו משקפים. מה אורכו? פעמיים ההיטל של הוקטור על הישר. אם כן, ראינו שלחבר את הוקטור עם השיקוף שלו נותן לנו את פעמיים ההיטל שלו. זה נותן לנו את המשוואה הכללית הבאה: אם \( v \) הוא וקטור, ואם \( a \) הוא וקטור יחידה בכיוון הישר שדרכו משקפים, אז \( \mbox{Ref}\left(v\right)+v=2\left\langle v,a\right\rangle a \), כלומר \( \mbox{Ref}\left(v\right)=2\left\langle v,a\right\rangle a-v \).

במילים אחרות, אופרטור השיקוף ביחס לציר \( a \) (כאשר \( a \) הוא וקטור יחידה) הוא האופרטור \( 2\left|a\right\rangle \left\langle a\right|-I \). נראה מוכר? בוודאי! השתמשנו באופרטור \( 2\left|\psi\right\rangle \left\langle \psi\right|-I \), כשהוא משורשר עם \( O \), בבנייה של \( G \) שלנו. אם כן, אחת משתי הפעולות שמרכיבות את \( G \) היא שיקוף - במקרה הנוכחי, שיקוף ביחס לציר \( \left|\psi\right\rangle \) שמתאר את הסופרפוזיציה האחידה.

מה עם \( O \)?

ובכן, הנה עוד דרך לחשוב על שיקופים. שיקוף הוא טרנספורמציה לינארית, ולכן מספיק לדעת איך הוא מתנהג על אברי בסיס של המרחב. כרגיל, נדבר על שיקוף ביחס לציר \( a \). איך השיקוף פועל על \( a \) עצמו? ובכן, הוא לא מזיז אותו בכלל, כלומר \( a\mapsto a \). לעומת זאת, איך השיקוף פועל על וקטור שמאונך ל-\( a \), נסמנו \( b \)? קל לראות שהסכום של \( b \) והשיקוף שלו יהיה 0, ולכן \( b\mapsto-b \). ניתוח מדויק של זה יש בפוסט שלי על ערכים עצמיים, שמשתמש בשיקוף בתור דוגמה - הערכים העצמיים הם 1 ו-\( -1 \), והוקטורים העצמיים הם הציר שדרכו משקפים והציר שמאונך לו.

ובכן, את האופרטור \( O \) הצגתי בדיוק באופן הזה: אם \( x \) הוא הוקטור שנותן \( f\left(x\right)=1 \) אז \( x\mapsto-x \) ואילו אם \( x \) הוא כל וקטור בסיס אחר, אז \( x\mapsto x \). תזכרו שאנחנו מדברים על המרחב שנפרש על ידי \( \left|\psi\right\rangle \) ו-\( \left|a\right\rangle \); במרחב הזה, הוקטור העצמי של 1 הוא בדיוק \( \sum_{x\ne a}\left|x\right\rangle \) (צירוף אחיד של כל הוקטורים במרחב, חוץ מ-\( \left|a\right\rangle \)). אחרי נרמול נקבל את הוקטור \( \left|e\right\rangle =\frac{1}{\sqrt{N-1}}\sum_{x\ne a}\left|x\right\rangle \).

אז הסכמנו ש-\( G \) מבצעת שתי פעולות שיקוף ולכן היא אכן מבצעת פעולת סיבוב. אבל סיבוב של כמה מעלות? ובכן, בתמונה מויקיפדיה שהבאתי למעלה מראים גם שהזווית שבה מסובבים היא פעמיים הזווית שבין הצירים שמשקפים ביחס אליהם. זה דורש הוכחה פורמלית, כמובן, אבל היא לא קשה במיוחד אלא בעיקר טכנית (אני לא חושב על משהו יותר מוצלח מאשר לכתוב את המטריצות המייצגות של הטרנספורמציות ולכפול אותן) ולכן אדלג עליה כאן. מה הזווית במקרה שלנו אמורה לצאת כבר ברור - \( 2\theta \). אז רק נותר להסביר למה הזווית בין צירי השיקוף היא \( \theta \).

נסמן \( \cos\gamma=\left|\left\langle e,\psi\right\rangle \right| \). החישוב הוא קל למדי: \( \left|\left\langle e,\psi\right\rangle \right|=\frac{1}{\sqrt{N}\sqrt{N-1}}\sum_{x\ne a}1=\sqrt{\frac{\left(N-1\right)^{2}}{N\left(N-1\right)}}=\sqrt{\frac{N-1}{N}} \). בואו ניזכר בזהות \( \sin^{2}x+\cos^{2}x=1 \), כלומר \( \sin x=\sqrt{1-\cos^{2}x} \). נקבל: \( \sin\gamma=\sqrt{1-\frac{N-1}{N}}=\frac{1}{\sqrt{N}}=\cos\alpha=\sin\theta \) - הפלא, ופלא, קיבלנו בדיוק את התוצאה המבוקשת!

האם סיימנו? בוודאי שלא!

הצלחנו להבין למה האלגוריתם עובד, ולטעמי ההסבר הזה היה אלגנטי ונפלא ורק בשבילו כל סדרת הפוסטים הזו הייתה שווה. אבל עדיין לא הסברנו איך אפשר לממש את האלגוריתם! השתמשתי בשתי פעולות שיקוף, אבל עבור אף אחד מהן לא הסברתי למה בכלל סביר שנוכל להפעיל אותה ברמת החישוב הקוונטי, שבו מותר לנו להשתמש בשערים קוונטיים על לא יותר מדי קיוביטים בבת אחת. אני אסביר עכשיו את הרעיון הבסיסי, אבל עדיין לא אסביר בדיוק איך אפשר לבנות את השערים הקוונטיים הרלוונטיים - זה עניין לפוסט נפרד - אבל נבין אילו שערים בערך צריך.

נתחיל עם \( 2\left|\psi\right\rangle \left\langle \psi\right|-I \). היצור הזה הוא שיקוף ביחס ל-\( \left|\psi\right\rangle \), ולכן כפי שכבר ראינו \( \left|\psi\right\rangle \) הוא וקטור עצמי של האופרטור הזה עם ערך עצמי 1, ואילו כל \( \left|x\right\rangle \) שניצב לו הוא וקטור עצמי עם ערך עצמי \( -1 \). הבעיה היא שהוקטורים הללו הם מסובכים והשערים הקוונטיים שלנו לא יודעים איך לפעול עליהם. אז משתמשים בהתחכמות הישנה ביותר בספר - מלכסנים. מבצעים שינוי בסיס. אם נכפול במטריצה \( H^{\otimes n} \), נעביר את \( \left|\psi\right\rangle \) לוקטור \( \left|00\dots0\right\rangle \), וכל וקטור שניצב ל-\( \left|\psi\right\rangle \) יעבור לוקטור בסיס אחר של אפסים ואחדים, רק ש-1 יופיע בוקטור לפחות פעם אחת. כעת אפשר יהיה לתאר את הפעולה באופן הבא:

\( \left|00\dots0\right\rangle \mapsto-\left|00\dots0\right\rangle \)

\( \left|x\right\rangle \mapsto\left|x\right\rangle \) אם \( \left|x\right\rangle \ne\left|00\dots0\right\rangle \)

מבחינה אלגוריתמית קלאסית זה חישוב די פשוט: עבור ביט-ביט, ואם מצאת 1, החזר את הקלט המקורי; אחרת, בסיום, החזר את שלילת הקלט המקורי. איך מבצעים את זה בעולם הקוונטי? זה, כאמור, עניין לפוסט ייעודי בנושא.

אחרי שמבצעים את הפעולה הזו, צריך לחזור לבסיס המקורי - מבצעים את זה על ידי כפל נוסף ב-\( H^{\otimes n} \). זה מסיים את התיאור של האופרטור \( 2\left|\psi\right\rangle \left\langle \psi\right|-I \).

מה עם האופרטור \( O \)? על פניו אפשר לומר שהוא נתון על ידי אורקל וחסל, אבל ההנחה שיש אורקל שעושה בדיוק את מה שאנחנו רוצים - הטלה - היא הנחה קצת חזקה מדי. מה אם כל מה שהאורקל יודע לעשות, בהינתן \( x \), הוא לחשב את \( f\left(x\right) \) ולשים לנו בקיוביט כלשהו? ובכן, “לשים בקיוביט” זה מונח בעייתי בחישוב קוונטי כי פירושו הוא “למחוק את התוכן הקודם של הקיוביט ולכתוב משהו חדש במקומו” וזו פעולה לא הפיכה, ולכן לא כזו שאפשר לממש. לכן תיאור יותר סביר של אורקל קוונטי הוא זה: המצב הקוונטי שלנו (החלקים ממנו שמעניינים אותנו) יהיה מצורה \( \left|x\right\rangle \left|q\right\rangle \) כאשר \( \left|q\right\rangle \) הוא קיוביט בודד שהאורקל יודע להתעסק בו. מה שהאורקל עושה הוא לבצע את החישוב הבא:

\( \left|x\right\rangle \left|q\right\rangle \mapsto\left|x\right\rangle \left|q\oplus f\left(x\right)\right\rangle \)

כאשר \( \oplus \) היא פעולת ה-XOR ההפיכה. כלומר, האורקל מחשב את \( f\left(x\right) \) ואם \( f\left(x\right)=0 \) לא נוגע ב-\( q \); אחרת, אם \( f\left(x\right)=1 \), הוא הופך את וקטורי הבסיס בצירוף הלינארי שמגדיר את \( \left|q\right\rangle \), דהיינו \( a\left|0\right\rangle +b\left|1\right\rangle \mapsto b\left|0\right\rangle +a\left|1\right\rangle \). זה, כאמור, הדבר הכי קרוב ל”חשב את \( f\left(x\right) \) וכתוב את התוצאה בקיוביט” שנוכל לצפות לו בחישוב קוונטי.

איך עוברים מזה אל האפקט של \( O \) שאנחנו רוצים, דהיינו \( \left|x\right\rangle \mapsto\left(-1\right)^{f\left(x\right)}\left|x\right\rangle \) ? ובכן, אנחנו יכולים להניח שאנחנו יודעים את הערך של \( \left|q\right\rangle \) בתחילת החישוב או אפילו קובעים אותו; אז אפשר יהיה להפעיל אופרטור קוונטי שיעביר את \( \left|q\right\rangle \) להיות \( \frac{\left|0\right\rangle -\left|1\right\rangle }{\sqrt{2}} \) (למשל, אם בהתחלה \( \left|q\right\rangle =\left|0\right\rangle \) אז נפעיל עליו NOT ולאחר מכן \( H \)).

כעת, מה קורה ל-\( \left|x\right\rangle \left(\frac{\left|0\right\rangle -\left|1\right\rangle }{\sqrt{2}}\right) \) כשמפעילים עליו את האורקל? אם \( f\left(x\right)=0 \) אז מקבלים את אותו מצב, כצפוי. אחרת, אם \( f\left(x\right)=1 \), הקיוביט של האורקל הופך ל-\( \left(\frac{-\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}}\right)=-\left(\frac{\left|0\right\rangle -\left|1\right\rangle }{\sqrt{2}}\right) \), ולכן מקבלים \( -\left|x\right\rangle \left(\frac{\left|0\right\rangle -\left|1\right\rangle }{\sqrt{2}}\right) \), וזהו בדיוק האפקט שרצינו!

זה מסיים עם האלגוריתם של גרובר. עכשיו, בנוסף להיכרות עם אלגוריתם מגניב בפני עצמו, אני מקווה שאנחנו מבינים קצת יותר טוב את אופי הפעולות שאנחנו צריכים לבצע בחישוב קוונטי; בפוסט הבא נדון בשאלת המימוש שלהן.