מבוא לדקדוקים חסרי הקשר

הפוסט על משפט נרוד מהווה לטעמי סיום הולם לנושא של שפות רגולריות, אבל מהנושא הזה יש קפיצה טבעית מאוד אל נושא קרוב ברוחו - שפות חסרות הקשר. בזמן שהכלי העיקרי שבו השתמשנו כדי לתאר שפות רגולריות היה אוטומטים, עבור שפות חסרות הקשר הכלי הזה הוא דקדוקים. באופן כללי דקדוקים הם דבר מאוד מועיל ומעניין שכדאי להציג ואפשר לגשת אליו בכמה דרכים שונות; בפוסט הזה אנקוט בדרך קצת מוזרה יחסית (אבל נחמדה, לטעמי, אחרת לא הייתי מציג אותה) שבה נגיע אל המושג של דקדוק מתוך המושג של ביטוי רגולרי.

בואו ניזכר מה זה ביטוי רגולרי. זה סימון שבא לתאר שפות, באופן הבא: \( \emptyset \) מסמן את השפה הריקה; \( \varepsilon \) מסמן שפה שהאיבר היחיד שלה הוא המילה הריקה, \( \sigma \) מסמן שפה שהאיבר היחיד שלה הוא המילה בעלת האות הבודדת \( \sigma \), ואם \( r_{1},r_{2} \) הם ביטויים רגולריים אז \( \left(r_{1}+r_{2}\right) \) מסמן את איחוד השפות שלהם, \( \left(r_{1}\cdot r_{2}\right) \) את שרשור השפות שלהם ו-\( \left(r_{1}^{*}\right) \) את סגור קלייני של שפת \( r_{1} \) - אוסף כל השרשורים של אפס או יותר מילים מהשפה של \( r_{1} \).

למשל, אם \( \Sigma=\left\{ a,b\right\} \) הוא האלפבית שלנו, אז שפת כל המילים מאורך זוגי מעל האלפבית הזה מתוארת על ידי הביטוי הרגולרי \( \left(\left(a+b\right)\left(a+b\right)\right)^{*} \). כאן כבר הרשיתי לעצמי להשמיט סוגריים ואת הסימן \( \cdot \).

עד עכשיו חשבנו על ביטויים רגולריים בתור כלי לתיאור של שפה, ואולי גם בתור מין “מתכון” לבניית אוטומט שמזהה אותה. עכשיו אני רוצה להציג דרך טיפה שונה להתבונן עליהן - בתור מתכון עבור אלגוריתם לייצור של מילים בשפה של הביטוי. האלגוריתם הולך לייצר את כל המילים בשפה, ורק אותן. כל הרצה שלו תסתיים אחרי מספר סופי של צעדים עם פלט שהוא אחת מהמילים בשפה, או שתודיע “נתקעתי” ולא תייצר מילה בריצה הזו, וריצות שונות ייבדלו זו מזו על ידי בחירות שונות שהאלגוריתם יכול לבצע בחלק משלביו.

כדי להבין איך זה הולך, בואו ניקח את הביטוי הרגולרי לשפת המילים מאורך זוגי ונחשוב על האופן שבו אפשר לייצג אותו במחשב, בצורה שהיא קצת יותר חכמה מסתם מחרוזת אלא כוללת מידע על המבנה שלו. אפשר לומר שיש משתנה כלשהו, נסמן אותו \( S \), שמייצג את כל הביטוי; ושיש משתנה \( A \) שמייצג את החלק שבין הסוגריים החיצוניים, כלומר \( S=A^{*} \). גם את \( A \) נוכל להציג בעזרת משתנה אחר, \( A=BB \); ואת \( B \) אפשר להציג בתור \( B=C+D \), כאשר \( C=a \) ו-\( D=b \).

כעת האלגוריתם פועל כך: התחילו עם \( S \). כעת, בחרו \( n\ge0 \) טבעי והחליפו את \( S \) ב-\( A^{n} \) (אם \( n=0 \) אז מחליפים את \( S \) ב-\( \varepsilon \)). כעת, לכל מופע של \( A \), החליפו אותו ב-\( BB \); כעת, לכל מופע של \( B \), החליפו אותו ב-\( C \) או החליפו אותו ב-\( D \). לבסוף, החליפו כל מופע של \( C \) ב-\( a \) וכל מופע של \( D \) ב-\( b \), והופה - קיבלתם מילה.

מה בעצם עשינו כאן? התחלנו מאיזה משתנה \( S \) וביצענו עליו פעולת שכתוב שהחליפה אותו במשתנים אחרים. גם עליהם הפעלנו פעולות שכתוב וכן הלאה וכן הלאה עד אשר קיבלנו אותיות ששייכות לאלפבית שלנו, ואותן כבר לא שכתבנו יותר. זה הרעיון הבסיסי מאחורי דקדוקים: יש לנו אוסף של משתנים, ואנחנו מבצעים עליהם פעולות שכתוב, עד שכל מה שנשאר לנו הוא רק אותיות-שאינן-משתנים. נכניס כבר עכשיו קצת טרמינולוגיה: לאותיות-שאינן-משתנים אני קורא טרמינלים (“טרמינלי” - סופי, שכן האותיות הללו מסיימות את סדרת פעולות השכתוב שלנו) ולפעולת השכתוב אני קורא “גזירה”. דקדוק מורכב מארבעה רכיבים - קבוצת משתנים, קבוצת טרמינלים, משתנה ספציפי שמתפקד בתור משתנה התחלתי (אצלנו זהו \( S \)) וקבוצת כללי גזירה אפשריים. עוד מעט יגיעו גם הגדרות פורמליות יותר.

יש נקודה מעניינת אחת שטרם התייחסתי אליה - מה קורה אם \( \emptyset \) מופיע כחלק מהביטוי הרגולרי? מה עושה המשתנה שלו? פשוט מאוד - למשתנה הזה לא יהיו כללי גזירה, ולכן אם הוא מופיע משהו במהלך גזירת מילה, “נתקענו” והאלגוריתם שלנו יעצור ויגיד “נתקעתי” (לא סתם הצעתי את האפשרות הזו קודם!). זכרו שביטוי כמו \( \emptyset^{*} \) לא מגדיר שפה ריקה, אלא את השפה שיש בה רק את \( \varepsilon \). זה מתאים לכך שאם \( A=B^{*} \) כך ש-\( B=\emptyset \) אז \( A \) יוכל לגזור את \( \varepsilon \) או את \( B^{n} \) עבור \( n\ge1 \), כשכל הגזירות מהצורה \( B^{n} \) “ייתקעו” ולכן נישאר רק עם \( \varepsilon \).

עכשיו, כשיש לנו פורמליזציה חדשה כלשהי, אפשר גם לבחון את הדרכים השרירותיות שבהן אנחנו מגבילים אותה ולראות מה קורה אם מסירים את המגבלות. במקרה שלנו המגבלות מגיעות בצורה כמעט סמויה מהאופן שבו אנחנו “מסיקים” את הדקדוק מתוך ביטוי רגולרי. ראשית, כל משתנה יכול לעשות בדיוק אחד מבין הדברים הבאים: או לגזור אחד מבין שני משתנים (אם \( A=B+C \)), או לגזור שני משתנים ברצף (עבור \( A=BC \)) או לגזור משתנה אחד \( n\ge0 \) פעמים (עבור \( A=B^{*} \)), או לגזור אות בודדת, או את המילה הריקה. או כלום. למה לא להרשות לו לעשות הרבה דברים שונים? מה רע בלגזור שלושה משתנים ברצף, למשל? או שתהיה יכולת לבחור בין גזירה של משתנה אחד לבין גזירה של שרשור של שני משתנים? אם נחשוב על זה קצת נראה שאפשר “לסמלץ” את היכולות הללו גם בעזרת הכללים הקיימים. למשל, אם אני רוצה ש-\( A \) יוכל לגזור את \( BCD \) אני יכול להוסיף “משתנה עזר” \( E \), את הגזירה שבה \( A \) גוזר את \( BE \) וגזירה שבה \( E \) גוזר את \( CD \). אם כן, ההגבלה האמיתית היא לא כאן. איפה היא כן?

אם אני מתחיל מלדבר על משתנים שגוזרים משתנים אחרים, אני לא אומר במפורש שום מגבלה על אילו משתנים יכול משתנה כלשהו לגזור. למשל, אני לא אוסר על משתנה לגזור את עצמו. ואני לא אוסר על סיטואציה שבה \( A \) גוזר את \( B \) ו-\( B \) גוזר את \( A \) בחזרה, וכדומה. כלומר, אני מאפשר “מעגלים”. במשתנים שמגיעים מביטוי רגולרי זה לא יכול לקרות, כי כל משתנה מייצג תת-ביטוי-רגולרי, כאשר \( B \) יכול להיגזר מ-\( A \) רק אם הביטוי של \( B \) קטן ממש מהביטוי של \( A \). זו המגבלה הקריטית. נניח לרגע שאני מעיף אותה - בואו תראו איך אני בונה בלי בעיה דקדוק עבור \( L=\left\{ a^{n}b^{n}\ |\ n\ge0\right\} \), שהיא הדוגמה לשפה לא רגולרית שאני משתמש בה כל הזמן. הדקדוק שלי יכלול משתנה יחיד \( S \), שגוזר את המילה \( aSb \) או את המילה \( \varepsilon \), וזהו. תנסו לפרמל אותו באמצעות סוגי כללי הגזירה שהצגתי - אני תכף אעשה את זה, אחרי שאציג את ההגדרות הפורמליות סוף כל סוף.

ובכן, מספיק עם המוטיבציה הרעיונית, בואו נעבור לניסוח המלא. דקדוק חסר הקשר הוא רביעייה \( G=\left(V,T,S,P\right) \) שכוללת קבוצה סופית של משתנים \( V \), קבוצה סופית של טרמינלים \( T \), משתנה התחלתי \( S\in V \) וקבוצה סופית של כללי גזירה \( P \), כאשר כלל גזירה הוא מחרוזת מהצורה \( A\to\alpha \) כאשר \( \alpha\in\left(V\cup T\right)^{*} \) הוא סדרה כלשהי של משתנים וטרמינלים. למשתנה יכולים להיות כמה כללי גזירה שונים שבהם הוא מופיע באגף שמאל, ולפעמים נוח לכתוב כמה מהם בבת אחת כשהם מופרדים על ידי קו אנכי. למשל, הדקדוק עבור \( \left\{ a^{n}b^{n}\ |\ n\ge0\right\} \) נכתב כך: \( S\to aSb|\varepsilon \). כאן \( V=\left\{ S\right\} \) ו-\( T=\left\{ a,b\right\} \) אבל לרוב אני לא אציין את הקבוצות הללו במפורש אלא רק אתן את כללי הגזירה של הדקדוק.

עכשיו צריך להסביר מהי גזירה - איך מילים מתקבלות על ידי הדקדוק. הרעיון בגזירה הוא שמתחילים מ-\( S \) ובכל צעד מבצעים שכתוב שבו עבור משתנה \( A \) כלשהו אנחנו בוחרים כלל גזירה כלשהו מהצורה \( A\to\alpha \) ומחליפים את \( A \) ב-\( \alpha \). פורמלית, אנחנו אומרים ש-\( \alpha\Rightarrow\beta \) אם \( \alpha=\gamma A\delta \) עבור \( A\in V \) כלשהו ו-\( \gamma,\delta\in\left(V\cup T\right)^{*} \), ו-\( \beta=\gamma\lambda\delta \) כך ש-\( A\to\lambda\in P \). זה פורמליזם קצת מתוסבך אבל הרעיון הוא בדיוק מה שאמרתי במילים לפני רגע.

כפי שאתם רואים, אני משתמש די הרבה בביטויים שהם סדרה כלשהי של משתנים וטרמינלים. אני אקרא להם בשם תבנית פסוקית, ובכך אני טיפה מרמה כי בכל מני מקומות משתמשים במילה הזו כדי לתאר רק סדרות של משתנים וטרמינלים שיכולות להופיע במהלך גזירה חוקית מדקדוק כלשהו. אני גם אשתמש באותיות יווניות קטנות כדי לתאר אותן, כך שאפשר יהיה להבין מההקשר למה אני מתכוון בלי שאומר זאת במפורש.

כעת, הגדרנו יחס \( \alpha\Rightarrow\beta \) בין שתי תבניות פסוקיות, שאומר שבדקדוק \( G \) אפשר לגזור את \( \beta \) מתוך \( \alpha \). בואו ניקח את הסגור הרפלקסיבי-טרנזיטיבי של היחס הזה ונסמן אותו ב-\( \Rightarrow^{*} \). זה נשמע מפוצץ, אבל המשמעות של \( \alpha\Rightarrow^{*}\beta \) היא מאוד פשוטה - קיים \( n\ge0 \) טבעי כך ש-\( \alpha\Rightarrow^{n}\beta \) כאשר \( \Rightarrow^{n} \) מציין בדיוק \( n \) צעדי גזירה (ב-0 צעדי גזירה תבנית פסוקית כלשהי “גוזרת” את עצמה). כעת אפשר להגדיר את השפה של דקדוק בתור אוסף כל המילים שמורכבות מטרמינלים בלבד שהדקדוק גוזר: \( L\left(G\right)=\left\{ w\in T^{*}\ |\ S\Rightarrow^{*}w\right\} \).

למה מה שהגדרתי נקרא “דקדוק חסר הקשר” ולא סתם “דקדוק”? ובכן, כי יש סוגים כלליים יותר של דקדוקים. באופן הכי כללי, כללי הגזירה של דקדוק לא חייבים להיות מהצורה \( A\to\alpha \) אלא מהצורה \( \alpha\to\beta \) כאשר \( \alpha \) היא תבנית פסוקית כלשהי שהדרישה היחידה שלנו עליה היא שהיא תכיל משתנה כלשהו (אפשר כמה). זה בעצם אומר שהאופן שבו משתנים נגזרים יכול להיות תלוי בהקשר שלהם (האותיות שנמצאות “סביבן” במילה). אני לא אציג את הדקדוקים הללו כרגע כי הם מעניינים מספיק כדי להצדיק דיון נפרד, שיגיע יותר מאוחר, אחרי שכבר נתרגל לדקדוקים חסרי הקשר.

עכשיו בואו נחזור לביטויים הרגולריים שלנו. הפורמליזם של דקדוק שהגדרתי מאפשר לנו לטפל ב-\( A=B+C \): זה יתורגם לכללי הגזירה \( A\to B|C \). כמובן שגם \( A=BC \) מטופל על ידי הגזירה \( A\to BC \). אבל מה עם \( A=B^{*} \)? על פניו אין לי משהו שיודע “לסמלץ” אותו בפורמליזם שלי. אבל בפועל כמובן שיש, כל עוד אין לי איסור על כך שמשתנה יגזור את עצמו: כללי הגזירה \( A\to BA|\varepsilon \) מסמלצים בדיוק את הקטע הזה של לגזור את \( B \) 0 או יותר פעמים. אם כן, כבר אנחנו רואים שבהינתן ביטוי רגולרי, קל לבנות דקדוק חסר הקשר שמייצר את אותה שפה כמוהו, ולכן השפות שמיוצרות על ידי דקדוקים חסרי הקשר מכילות את כל השפות הרגולריות - אבל יש עוד שפות, למשל \( \left\{ a^{n}b^{n}\ |\ n\ge0\right\} \). זה מצדיק מתן שם נפרד למחלקה הזו: מחלקת השפות חסרות ההקשר כוללת את כל השפות שקיים דקדוק חסר הקשר שמייצר אותן. בהמשך נראה ש-\( \left\{ a^{n}b^{n}c^{n}\ |\ n\ge0\right\} \) אינה שפה חסרת הקשר, כך שלמרות שקיבלנו מחלקה גדולה יותר מהשפות הרגולריות, היא עדיין לא גדולה מדי ויש שפות פשוטות יחסית שאינן שם.

דקדוקים חסרי הקשר הם דרך מאוד נוחה לתאר שפות בצורה יחסית קריאה וברורה - שפות תכנות מתוארות לרוב בצורה פורמלית באמצעות דקדוק, והמהדר שממיר קוד בשפת התכנות לשפת מכונה משתמש בדקדוק הזה כדי להבין מה התוכנית אומרת. זה רומז לנו שדקדוק לא סתם מתאר מילה אלא גם אומר לנו משהו על המבנה של המילה הזו - מן הסתם מכאן השם “דקדוק” מגיע מלכתחילה; אבל מכיוון שההבנה שלי בלשונאות ובדקדוקים לשפות טבעיות היא אפסית, אני לא אדבר על דקדוקים “אמיתיים” בכלל אלא אדבוק באלו הפורמליים. ויש לי דוגמה פשוטה שאני חושב שתבהיר היטב את עניין המבנה הזה - ביטויים חשבוניים. ביטוי חשבוני לדוגמה הוא \( 5+3\times8 \), שערכו המספרי הוא 29. הביטוי הזה הוא גם מילה, כשה”אותיות” שלנו הם מספרים וסימני החשבון. בואו ניתן דקדוק פשוט עבור השפה הזו. כדי לייצר מספרים אני אשתמש במשתנה \( V \) עם הגזירות \( V\to VV|0|1|2|3|4|5|6|7|8|9 \) - הבהירו לעצמכם למה זה מספיק כדי לייצר כל מספר (וגם יכול לייצר מספרים מהצורה 0013 אבל זה מספיק לא בעייתי כדי שלא אטרח לתקן את זה - וכמובן שקל לתקן, עם עוד משתנה עזר). כעת, כדי לייצר ביטוי חשבוני, נשתמש בהגדרה כמו-רקורסיבית: ראשית, כל מה ש-\( V \) יכול לייצר הוא ביטוי חשבוני; שנית, אם \( E \) הוא ביטוי חשבוני ו-\( \oplus \) היא פעולה חשבונית כלשהי, אז \( E\oplus E \) גם הוא ביטוי חשבוני. אם כן, נוסיף משתנה \( E \) שיהיה גם המשתנה ההתחלתי שלנו, ואת כללי הגזירה \( E\to V|E+E|E\times E|E-E|E\div E \).

ועכשיו, כיצד ניתן לגזור את \( 5+3\times8 \)? הנה דרך אחת לעשות את זה (אני קופץ על כמה צעדים כשנוח לי):

\( E\Rightarrow E+E\Rightarrow E+E\times E\Rightarrow^{*}V+V\times V\Rightarrow^{*}5+3\times8 \)

אבל יש עוד דרך לעשות את זה! דרך שהיא בבירור שונה:

\( E\Rightarrow E\times E\Rightarrow E+E\times E\Rightarrow^{*}V+V\times V\Rightarrow^{*}5+3\times8 \)

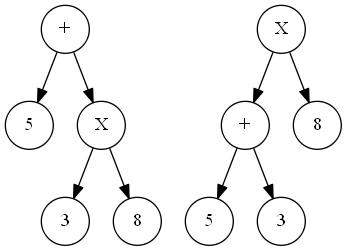
ההבדל הוא שבדרך הראשונה התחלנו עם החיבור, ובדרך השניה התחלנו עם הכפל. על פניו זה לא נראה כזה שונה, אבל באופן ציורי קל לראות את ההבדל. אני הולך לצייר את עץ הגזירה של שתי הגזירות הללו. עץ גזירה הוא דרך גרפית נאה לצייר גזירות בצורה קומפקטית - בלי להיכנס לפורמליזם, זה עץ שבו כל צומת פנימי מתאים למשתנה שהופיע מתישהו בגזירה, והבנים שלו הם התווים שהוא גזר. כפי שתוכלו לראות, לשתי הגזירות השונות הללו יש עצי גזירה שונים:

עץ גזירה הוא מה שמתאר את ה”מבנה” של המילה שנגזרה. במקרה של ביטוי חשבוני, אפשר לחשב את הערך של הביטוי עם עץ הגזירה, בצורה מתבקשת: הערך של עלה הוא ערך המספר שלו (אצלי זה טיפה יותר מסובך כי מספר יכול להיות מיוצג על ידי כמה עלים, אבל תתעלמו מזה או תחשבו על המקרה שבו כל המספרים הם בני ספרה אחת). הערך של צומת פנימי מתקבל מהפעלת האופרטור שכתוב באותו צומת פנימי על שני הבנים שלו. קל לראות שבעץ הגזירה הימני הערך שנקבל הוא \( 29 \), אבל בעץ הגזירה השמאלי הערך שנקבל הוא בכלל \( 64 \). מה הלך פה? ובכן, ראינו שאת הביטוי \( 5+3\times8 \) יש שתי דרכים שונות מהותית לקרוא - זאת על פי סדר הקדימויות שאנחנו נותנים לאופרטורים - האם כפל בא קודם (השמאלי) או חיבור (הימני).

הסיטואציה הזו, של דקדוק שבו קיימת מילה עם שני עצי גזירה שונים או יותר, נקראת רב-משמעות של דקדוק והיא לרוב לא רצויה. תחשבו על זה בשפת תכנות - זה אומר שאותה תוכנית מחשב יכולה לעבור הידור לשתי תוכניות שעושות דברים שונים, בהתאם למוזריות של המהדר הספציפי. לכן לרוב משתדלים לבנות דקדוק שיהיה חד משמעי ולא רב משמעי - עבור שפת הביטויים החשבוניים יש כזה, ואציג אותו בפוסט נפרד, מאוחר יותר, שיעסוק קצת יותר בענייני הרב משמעויות הללו.

בואו נחזור לדבר עכשיו על ביטויים רגולריים. ראינו שאפשר לחשוב על ביטויים רגולריים בתור בערך דקדוק עם כל מני הגבלות מוזרות שלא נעים לנסח. האם אפשר למצוא מחלקה פשוטה יותר לתיאור של דקדוקים שהשפות שלהם הן בדיוק כל השפות הרגולריות? כמובן. והדקדוקים הללו יפעלו בצורה שמאוד דומה לסימולציה של אוטומט סופי דטרמיניסטי. אכנה את הדקדוקים הללו דקדוקים לינאריים ימניים. דקדוק הוא לינארי ימני אם כל כללי הגזירה שלו הם מהצורה \( A\to aB \) או \( A\to\varepsilon \) כאשר \( a \) הוא טרמינל ו-\( B \) הוא משתנה. כלומר, בכל צעד גזירה המשתנה הנוכחי גוזר אות אחת ומשתנה אחד, או מחליט שהספיק לו ומתפוגג (גוזר את \( \varepsilon \)) גזירה בדקדוק הזה נראית כמו כתיבה משמאל לימין של המילה (ומכאן שם הדקדוק - לינארי, כלומר בקו ישר, וימני, כלומר הולך ימינה):

\( S\Rightarrow aA\Rightarrow abB\Rightarrow abc \)

האם אתם רואים את הדמיון לאוטומט סופי דטרמיניסטי? הרי גם אוטומט כזה קורא את המילה שלו מימין לשמאל, ויש לו “מצב” שמשתנה בכל צעד, כמו שלדקדוק הלינארי הימני יש “מצב” שמשתנה בכל צעד ומתבטא בזהות המשתנה היחיד שנמצא בקצה הימני של המילה. ההבדל העקרוני הוא שאוטומטים מזהים מילים (רצים על כל המילה ואז עונים כן או לא) ואילו דקדוקים מייצרים מילים. אבל קל לגשר על ההבדלים הללו ולכל אוטומט סופי דטרמיניסטי \( A \) לבנות דקדוק לינארי ימני שקול \( G \), וההפך. בואו נראה את הבניות הללו.

נתחיל מבניה של אוטומט \( A \) עבור דקדוק \( G=\left(V,T,S,P\right) \) נתון. הרעיון יהיה לנסות ולסמלץ גזירה בדקדוק תוך כדי קריאת המילה. המצב של האוטומט יהיה המשתנה של הדקדוק, והאוטומט יבחר באופן אי דטרמיניסטי גזירה כלשהי שאפשרית מהמשתנה הנוכחי ומייצרת את האות שהוא כרגע קורא. הנה האוטומט: \( A=\left(V,T,S,\delta,F\right) \). כלומר, \( Q=V \) ו-\( \Sigma=T \) ו-\( q_{0}=S \), אם להשתמשב בסימנים שאנחנו רגילים אליהם מאוטומטים.

נותר רק לתאר את \( \delta \) ואת \( F \). ראשית, \( \delta\left(A,a\right)=\left\{ B\in V\ |\ A\to aB\in P\right\} \); ושנית, \( F=\left\{ A\in V\ |\ A\to\varepsilon\in P\right\} \). עכשיו צריך להוכיח זה עובד, ועושים את זה בצורה סטנדרטית: מוכיחים שמתקיים \( \hat{\delta}\left(A,w\right)=B \) אם ורק אם \( A\Rightarrow^{*}wB \), באינדוקציה על אורך \( w \), ולכן \( \hat{\delta}\left(S,w\right)=B \) כאשר \( B\in F \) אם ורק אם \( S\Rightarrow^{*}wB\Rightarrow w \), כלומר \( w\in L\left(A\right) \) אם ורק אם \( w\in L\left(G\right) \).

בכיוון השני, נניח שיש לנו אוטומט סופי דטרמיניסטי \( A=\left(Q,\Sigma,q_{0},\delta,F\right) \). נבנה דקדוק שמחקה ריצה של האוטומט על מילה כלשהי, וגוזר אפסילון רק אם האוטומט הגיע למצב מקבל. כלומר, \( G=\left(Q,\Sigma,q_{0},P\right) \) כאשר לכל \( q\in Q \) ו-\( \sigma\in\Sigma \) נסמן \( \delta\left(q,\sigma\right)=p \) ונוסיף את כלל הגזירה \( q\to\sigma p \), וכמו כן אם \( q\in F \) נוסיף את הגזירה \( q\to\varepsilon \). גם כאן הוכחת הנכונות דומה.

לסיום המבוא הזה, בואו נציג עוד דוגמה לדקדוק שסוגרת את המעגל שהתחלנו ממנו. התחלנו מביטויים רגולריים? אז בואו נציג דקדוק שגוזר ביטויים רגולריים! המבנה הרקורסיבי שלהם הופך את העניין לפשוט מאוד, כמובן: \( S\to\emptyset|\varepsilon|\sigma_{1}|\dots|\sigma_{n}|\left(S+S\right)|\left(S\cdot S\right)|\left(S^{*}\right) \).