שפות חסרות הקשר - למת הניפוח, הלמה של אוגדן ושפות רב משמעיות

אני ממשיך לדבר על תכונות שונות ומשונות של שפות חסרות הקשר, וממשיך עם האנלוגיה לשפות רגולריות. אחד מהדברים שעשינו בשפות רגולריות היה להוכיח משהו שנקרא “למת הניפוח”, שהצביע על סוג של תבניתיות שכל שפה רגולרית חייבת לקיים. משהו מאוד דומה קיים גם עבור שפות חסרות הקשר, אבל כרגיל עם שפות חסרות הקשר, זה קצת יותר מסובך. אני אראה את המשהו המאוד דומה. ואז אני אכליל אותו עוד קצת. ואז אני אשתמש בהכללה כדי להראות משהו שנראה בלתי קשור בעליל. בלמת הניפוח לשפות רגולריות השתמשנו כדי להוכיח ששפות אינן רגולריות, ובאופן דומה אפשר להשתמש בלמת הניפוח לשפות חסרות הקשר כדי להוכיח ששפות אינן חסרות הקשר; אבל אני אוכיח גם משהו שונה לחלוטין - ששפה חסרת הקשר מסויימת היא רב-משמעית טבועה, דהיינו שכל דקדוק עבור השפה בהכרח יהיה רב משמעי (אזכיר את כל ההגדרות בהמשך). זה שימוש יפה שאני מאוד מחבב כי על פניו בכלל לא ברור מה הקשר.

.נתחיל עם להיזכר מה הלך בשפות רגולריות. שם, בהינתן שפה רגולרית \( L \), הוכחנו שקיים \( n \) טבעי כך שלכל מילה \( z\in L \) המקיימת \( \left|z\right|\ge n \) קיים פירוק \( z=uvw \) כך ש-\( \left|uv\right|\le n \) ו-\( \left|v\right|\ge1 \) ו-\( uv^{i}w\in L \) לכל \( i\ge0 \). הרעיון מאחורי ההוכחה היה פשוט ויפה - ניקח אוטומט עבור השפה, ונריץ אותו על מילה ארוכה מספיק - מתישהו בהכרח תהיה בריצה “לולאה” (מצב כלשהו שהופיע פעמיים), ואז נוכל לקחת את תת-המילה שהאוטומט קרא על הלולאה ולהעלים אותה או לחזור עליה כמה פעמים שנרצה, ועדיין נקבל את המילה.

הרעיון של למת הניפוח לשפות חסרות הקשר הוא בדיוק אותו דבר, אבל בהקשר קצת שונה - לא של אוטומט (אמנם הצגתי אוטומט מחסנית עבור שפות חסרות הקשר, אבל אני לא אשתמש בו כאן), אלא של דקדוק חסר הקשר. מה שארצה לומר הוא שאם דקדוק חסר הקשר מייצר מילה שהיא ארוכה מספיק, אז בעץ הגזירה של המילה יהיה חייב להיות מסלול ארוך מאוד - כל כך ארוך, עד שמשתנה כלשהו של הדקדוק יופיע בו פעמיים. כלומר, יהיה משתנה שגוזר “את עצמו ועוד קצת”. ואז נוכל לוותר על הגזירה הזו או לחזור עליה כמה פעמים שנרצה, ובכך להשיג אפקט ניפוח שדומה לזה של הלמה עבור שפות פורמליות, אבל הניסוח המדוייק שלו קצת יותר מסובך. בואו ניתן את הניסוח הזה:

אם \( L \) היא שפה חסרת הקשר אז קיים \( n \) טבעי כך שלכל מילה \( z\in L \) קיים פירוק \( z=uvwxy \) כך ש-\( \left|vwx\right|\le n \) ו-\( \left|vx\right|\ge1 \) ו-\( uv^{i}wx^{i}y\in L \) לכל \( i\ge0 \).

במבט ראשון זה קצת מפחיד - יש פה פתאום פירוק לחמישה חלקים במקום שלושה, והניפוח הוא של שני חלקים בו זמנית, וכל העסק נראה מוזר - אבל אחרי שנראה את ההוכחה נבין למה זה טבעי ופשוט למדי. בינתיים, תרגיל פשוט כדי לידד אתכם עם הניסוח החדש - תוכיחו שאם שפה מקיימת את למת הניפוח לשפות רגולריות, אז היא מקיימת את למת הניפוח לשפות חסרות הקשר (“מקיימת את למת הניפוח” פירושו, “מקיימת את החלק של ה”אז קיים”, בלי להתחייב על ה”אם”).

כדי להוכיח את הלמה אני צריך לקחת דקדוק עבור \( L \), אבל כדי שהחיים יהיו קלים אני לא לוקח סתם דקדוק, אלא דקדוק שנמצא בצורה נורמלית פשוטה מאוד - הצורה הנורמלית של חומסקי. דקדוק בצורה הזו כולל רק שני סוגים של כללי גזירה: \( A\to a \) או \( A\to BC \). כלומר, משתנה יכול או לגזור אות אחת, או להתפצל לשני משתנים. שימו לב שדקדוק בצורה הנורמלית הזו לא יכול לגזור את \( \varepsilon \) כך שאני מניח לכאורה ש-\( L \) לא כוללת את \( \varepsilon \), אבל זה לא ממש משנה - אם \( L \) כוללת את \( \varepsilon \) אני אוכיח את למת הניפוח על \( L\backslash\left\{ \varepsilon\right\} \) והמסקנה שאקבל תהיה תקפה גם עבור \( L \) באותה מידה (כי אני אקח \( n\ge1 \) ולכן \( \varepsilon \) ממילא לא רלוונטית).

כמובן, צריך להסביר למה לכל שפה חסרת הקשר בלי \( \varepsilon \) יש דקדוק מהצורה הנורמלית של חומסקי. אני אקדיש לזה בדיוק פסקה אחת, ואתם לא חייבים להבין אותה ואם אתם מסתבכים פשוט תדלגו הלאה. האינטואיציה לא קשה - כל גזירה שמערבת גם משתנים וגם טרמינלים אפשר להחליף בגזירה שיש בה רק משתנים על ידי הוספת משתני עזר. למשל, אם יש לי את הגזירה \( A\to BaC \) אני יכול להוסיף משתנה עזר חדש \( A_{a} \) שהגזירה היחידה שלו היא \( A_{a}\to a \) ואז להחליף את הגזירה הנתונה ב-\( BA_{a}C \). עכשיו, אם יש לי גזירה של שלושה משתנים או יותר, אני יכול “להקטין” אותה בעזרת משתני עזר. למשל, אם \( A\to B_{1}B_{2}B_{3}B_{4} \) אני אוסיף משתני עזר חדשים \( C_{1},C_{2},C_{3} \) ואת הגזירות \( A\to B_{1}C_{1} \) ו-\( C_{1}\to B_{2}C_{2} \) ו-\( C_{3}\to B_{3}B_{4} \). אז בעצם, הדבר היחיד שמסובך לטפל בו הוא גזירות מהצורה \( A\to B \) (גזירות כאלו נקראות “כללי יחידה”) וגזירות מהצורה \( A\to\varepsilon \). מגזירות כאלו תמיד אפשר להיפטר באופן דומה לאיך שנפטרים מכללי-\( \varepsilon \) באוטומט סופי דטרמיניסטי - קודם כל מגלים את כל המשתנים \( B \) שעבורם מתקיים \( A\Rightarrow^{*}B \) (סתם לקחת משתנים כך ש-\( A\to B \) לא מספיק, כי מה קורה אם \( B\to C \)? אז נקבל ש-\( A\Rightarrow^{*}C \) - זה דומה ל”סגור-\( \varepsilon \)” עבור שפות רגולריות), ועכשיו מוסיפים לדקדוק את כל הגזירות מהצורה \( A\to\alpha \) כך ש-\( B\to\alpha \) היה גזירה בדקדוק המקורי. לבסוף, מעיפים את כל כללי היחידה. באופן דומה אפשר גם לטפל בגזירות מהצורה \( A\to\varepsilon \) - קודם כל מגלים את כל המשתנים שהם “אפיסים”, כלומר \( A\Rightarrow^{*}\varepsilon \), ואחר כך לכל גזירה \( A\to X_{1}X_{2}\dots X_{n} \) (כאשר כל \( X \) כזה יכול להיות או משתנה או טרמינל) מחליפים אותה בכל הגזירות מהצורה \( A\to Y_{1}\dots Y_{n} \) כאשר \( Y_{i}=X_{i} \) אם \( X_{i} \) לא אפיס, ו-\( Y_{i}\in\left\{ \varepsilon,X_{i}\right\} \) אם הוא כן. ואז מסירים את כל הגזירות מהצורה \( A\to\varepsilon \) מהדקדוק.

\( S\Rightarrow^{*}uAy \) עבור משתנה \( A \) כלשהו.

\( A\Rightarrow^{*}vAx \)

\( A\Rightarrow^{*}w \)

זה מסביר את המבנה ה”מוזר” של הפירוק. בואו נגיד במילים מה הם שלושת הדברים הללו: יש בדקדוק משתנה \( A \) שגוזר את עצמו, ואותו המשתנה ניתן לגזירה מתוך \( S \), ובנוסף הוא יודע לגזור מילה טרמינלית. כאשר גוזרים אותו מתוך \( S \) נסמן ב-\( u,y \) את “מה שמתפזר לצדדים”, ובאופן דומה כאשר \( A \) גוזר את עצמו נסמן ב-\( v,x \) את “מה שמתפזר לצדדים”, וב-\( w \) אנחנו מסמנים את המילה הטרמינלית שאנחנו יודעים שהוא יודע לגזור. אם הראינו את שלושת הדברים הללו, ברור שאפשר לייצר את \( uv^{i}wx^{i}z \) לכל \( i\ge0 \): על ידי ביצוע הגזירה \( S\Rightarrow^{*}uAy \), הפעלה \( i \) פעמים של הגזירה \( A\Rightarrow^{*}vAx \) ולבסוף הפעלה אחת של \( A\Rightarrow^{*}w \).

עיקר האתגר יהיה להוכיח ש-\( A \) כזה קיים בכלל. הרעיון הוא כזה: אם \( z \) היא מילה גדולה מספיק, אז עץ הגזירה שלה יהיה חייב להיות עמוק, מסיבה שאסביר בהמשך. בואו נסמ ב-\( k=\left|V\right| \) את גודל קבוצת המשתנים של הדקדוק. אם אצליח לגרום לכך שהמסלול העמוק ביותר בעץ יהיה בן לפחות \( k+1 \) צמתים פנימיים, זה מבטיח שיהיה משתנה שמופיע עליו פעמיים (זכרו - בעץ גזירה הצמתים הפנימיים הם משתנים, והעלים הם טרמינלים). המשתנה הזה יהיה ה-\( A \) שלי. כדי להבטיח את הטענה על כך ש-\( \left|vwx\right|\le n \) אני אצטרך לבחור משתנה שמופיע פעמיים והוא “נמוך ככל האפשר” בעץ (קרוב ככל האפשר לעלים). בואו עכשיו ניגש לפורמליזציה.

הפואנטה של שימוש בצורה הנורמלית של חומסקי היא שעץ הגזירה הוא בעל צורה מאוד ספציפית - הוא עץ בינארי, כלומר לכל צומת יש שני בנים, פרט לצמתים שהבנים שלהם הם עלים, ולצמתים כאלו יש רק בן יחיד. מה שנחמד בעצים בינאריים (ובאופן כללי, בעצים שבהם יש חסם קבוע על מספר הבנים של צומת) הוא שקל לקשור בין מספר העלים של העץ ובין העומק שלו. בואו ניקח לרגע עץ בינארי מושלם, שפירושו שכל העלים בעץ הם באותו עומק, וכל צומת שאינו עלה הוא בעל שני בנים. נניח שהעומק שלו הוא \( d \), כלומר שאורך המסלול מהשורש אל עלה כלשהו הוא בן \( d \) צעדים (ולכן אנחנו רואים בדרך \( d+1 \) צמתים). כמה עלים יש לעץ? הכי קל לעבוד עם מקרים פרטיים: עבור \( d=0 \) העץ כולו כולל רק צומת יחיד. עבור \( d=1 \) יש לנו את השורש ושני בנים. עבור \( d=2 \) לכל אחד משני הבנים יש שני בנים, ולכן יש ארבעה עלים. עבור \( d=3 \) כל אחד מארבעת העלים הוא עכשיו אב גאה לשני בנים נוספים, ולכן יש שמונה עלים… הבנתם את העיקרון. בעץ בינארי מושלם מעומק \( d \) יש בדיוק \( 2^{d} \) עלים. זה אומר שאם יש לנו עץ בינארי כלשהו (לאו דווקא מושלם) שבו יש יותר מ-\( 2^{d} \) עלים, אז בהכרח העומק שלו גדול מ-\( d \).

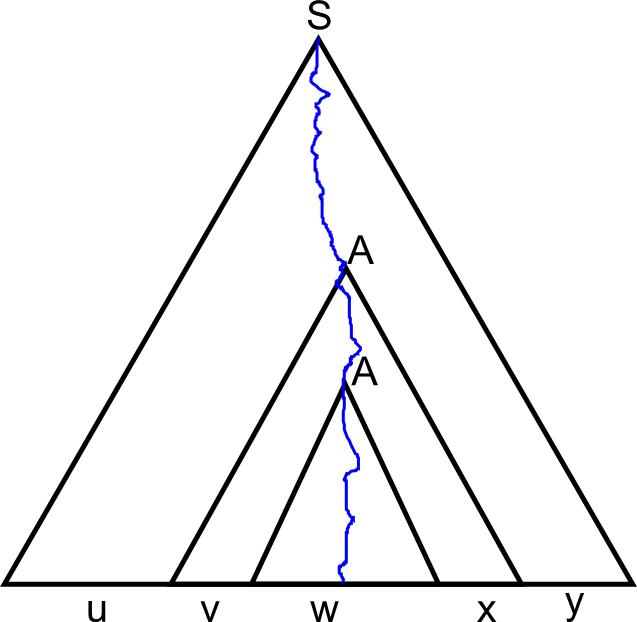
אז מה שנעשה, אם \( k \) הוא מספר המשתנים של הדקדוק שלנו, נבחר \( n=2^{k} \). עכשיו בואו ניקח עץ גזירה כלשהו עבור \( z \). אם נעיף את הצמתים של הטרמינלים, נקבל עץ בינארי שבו העלים הם המשתנים שהגזירה שהם ביצעו היא גזירה של טרמינלים. מכיוון שכל משתנה כזה גזר טרמינל אחד, מספר המשתנים הללו הוא בדיוק \( \left|z\right| \), כלומר מספר העלים בעץ הוא לפחות \( 2^{k} \), ולכן עומק העץ הוא לפחות \( k \). ניקח את המסלול הארוך ביותר בעץ - מכיוון שהעומק שלו הוא לפחות \( k \), הרי שכשאנחנו הולכים עליו אנחנו רואים לפחות \( k+1 \) משתנים. מסקנה - קיימים משתנים שמופיעים פעמיים על המסלול הזה. בואו נתחיל ללכת על המסלול מהעלה לכיוון השורש, ונסמן ב-\( A \) את המשתנה הראשון שמופיע פעמיים. עכשיו אפשר לתת את פירוק המילה שלנו - נסמן ב-\( w \) את המילה שהמופע השני, הנמוך יותר, של \( A \) גוזר; על כן המופע הראשון של \( A \) גוזר מילה ש-\( w \) היא חלק ממנה, ונסמן את החלקים שלפני ואחרי \( w \) ב-\( v,w \) בהתאמה, כלומר \( A \) הראשון גוזר את המילה \( vwx \). המילה הזו היא בתורה חלק מהמילה ש-\( S \) גוזר (כלומר, המילה של עץ הגזירה כולו) ונסמן את הלפני ואחרי ב-\( u,y \), כלומר המילה כולה היא \( uvwxy \) - הנה הפירוק שלנו. זה מאוד מבלבל אז הנה תמונה:

עכשיו מגיע הטיעון העדין ביותר בהוכחה. אני טוען שמבין שני המופעים של \( A \) שראינו, הגבוה יותר הוא כזה שתת-העץ שלו הוא מגובה \( k \) לכל היותר. זה נובע משני דברים. ראשית, אני טוען שהגובה של ה-\( A \) הזה על המסלול העמוק ביותר הוא לא יותר מ-\( k \). זה די ברור, מכיוון שאם הגובה היה יותר מ-\( k \), אז עוד לפני שהיינו מגיעים אל המופע הגבוה יותר של \( A \) כבר היינו רואים \( k+1 \) משתנים, ולכן היה משתנה אחר שכבר היה מופיע פעמיים והיינו רואים אותו. כעת, בנוסף לכך, אני צריך לטעון שאין מסלול אחר שעובר דרך ה-\( A \) הזה ומגיע לעלים, והוא ארוך יותר מ-\( k \) - זה נובע מכך שהמסלול שלקחתי היה המסלול העמוק ביותר ולכן אין מסלול שיותר עמוק ממנו. אני מתעכב על הטיעון הזה כי זו הנקודה שבה אני טעיתי בעבר שוב ושוב כאשר הצגתי את המשפט: פשוט אמרתי משהו בסגנון “עומק העץ הוא לפחות \( k \) אז קיים מסלול שבו יש משתנה שמופיע פעמיים”. זה נכון, אבל לא מבטיח לנו שהמופע הראשון מבין השניים של המשתנה הזה יהיה נמוך יחסית - מגובה \( k \) לכל היותר.

ולמה זה חשוב, שהוא מגובה \( k \) לכל היותר? כי זה מגביל את מספר העלים בתת-העץ שלו להיות לכל היותר \( 2^{k} \). ותת העץ הזה הוא בדיוק תת-העץ שמייצר את \( vwx \) שלנו, כך שאנחנו מקבלים את הדרישה \( \left|vwx\right|\le n \). אם לא היה אכפת לנו מהדרישה הזו (שנראית קצת מלאכותית במבט ראשון) ההוכחה הייתה יותר קלה כי לא היינו צריכים את כל הנימוקים העדינים הללו, אבל הדרישה הזו מאוד מועילה לנו כשאנחנו רוצים להשתמש בלמה (כמו הדרישה הדומה ש-\( \left|uv\right|\le n \) בלמת הניפוח לשפות רגולריות) ולכן התעקשנו עליה.

עדיין צריך להסביר למה \( \left|vx\right|\ge1 \) וזה לא לגמרי מובן מאליו. הטענה היא שכאשר \( A \) הראשון גוזר את \( A \) השני, חייב להיות משהו ש”ייגזר בצד”, כלומר לא ייתכן שהגזירה היא מהצורה \( A\Rightarrow^{*}A \). בדקדוקים כלליים אין לנו משהו שיבטיח את זה, אבל בצורה הנורמלית של חומסקי זה קל. הגזירה שה-\( A \) הראשון מבצע בצעד הראשון שלו חייבת להיות מהצורה \( A\Rightarrow BC \), ועכשיו אם (בלי הגבלת הכלליות) \( A \) השני הוא בתת-העץ של \( B \), אז בתת-העץ של \( C \) יהיה לפחות טרמינל אחד (כי \( C \) יודע רק לגזור שני דברים: או טרמינל, או עוד משתנים שמחוייבים בתורם לגזור משתנים או טרמינלים). אין ל-\( C \) דרך פשוט “להעלים את עצמו”.

זה מסיים את ההוכחה של למת הניפוח לשפות חסרות הקשר. בואו נראה עכשיו דוגמה זריזה לשימוש בה, בלי להיכנס לכל הפרטים - נוכיח ש-\( L=\left\{ a^{n}b^{n}c^{n}\ |\ n\ge0\right\} \) היא לא חסרת הקשר. לצורך כך נניח בשלילה שהיא חסרת הקשר, יהא \( n \) שקיומו מובטח על ידי הלמה ונסתכל במילה \( z=a^{n}b^{n}c^{n} \). אנחנו צריכים להראות שאפשר “לקלקל” כל פירוק אפשרי שלה. הנקודה היא שפירוק \( z=uvwxy \) כלשהו חייב להיות מאחת מחמש צורות אפשריות, בגלל המגבלה \( \left|vwx\right|\le n \): או ש-\( vwx \) חי כולו בתוך אחד משלושת הרצפים \( a^{n},b^{n},c^{n} \), או שהוא נמצא אי שם בתוך הרצף \( a^{n}b^{n} \) וחוצה אותו באמצע, או שהוא נמצא בתוך הרצף \( b^{n}c^{n} \) וחוצה אותו באמצע. בכל מקרה אין ל-\( vwx \) יכולת לכלול בתוכו גם \( a \)-ים, גם \( b \)-ים וגם \( c \)-ים כי זה יצריך ממנו להכיל לפחות \( n+2 \) תווים (לפחות \( a \) אחד, לפחות \( c \) אחד ואת כל ה-\( b^{n} \) שבאמצע) ולכן אם נבחר \( i=0 \) בהכרח נקבל מילה שמספר האותיות משלושת הסוגים בה לא מאוזן (כי הקטנו לפחות סוג אחד של אותיות, אבל באחד מהסוגים לא נגענו).

יש הכללה מאוד ברורה של הלמה שלא כל כך קשה להבין. הרעיון בה הוא שיש לנו קצת יותר שליטה על המיקום של ה-\( vwx \), שכרגע כל מה שאנחנו יודעים עליו זה שהוא מאורך לכל היותר \( n \) ונמצא במקום כלשהו במילה (בניגוד ללמת הניפוח לשפות רגולריות, ששם הוא היה חייב להיות בהתחלה). הרעיון הוא שאם \( z \) היא יותר ארוכה מ-\( n \), אז אין צורך להסתכל על כל \( z \) כדי להפעיל את הלמה; מספיק להסתכל על מקום כלשהו שהוא ארוך מ-\( n \) והלמה תפעל עליו. אבל למעשה, אפילו לא חייבים \( n \) תווים רציפים; אפשר להסתכל על כל סדרה של \( n \) תווים, גם לא רציפים, ולדבר על החלק מעץ הגזירה שמייצר את כל התווים בסדרה הזו. החלק הזה יהיה חייב להיות עמוק מספיק, וכן הלאה וכן הלאה. אז הנה הניסוח הפורמלי: בהינתן שפה חסרת הקשר \( L \) קיים קבוע \( n \) כך שלכל מילה \( z\in L \) ולכל בחירה של לפחות \( n \) תווים ב-\( z \), שנקרא להם “מסומנים”, קיים פירוק \( z=uvwxy \) כך ש-\( vwx \) כולל לכל היותר \( n \) תווים מסומנים, \( vx \) כולל לפחות תו מסומן אחד, ו-\( uv^{i}wx^{i}z\in L \) לכל \( i\ge0 \). למת הניפוח לשפות רגולריות היא פשוט מקרה פרטי של זה כאשר כל התווים של \( z \) הם מסומנים.

ההכללה הזו נקראת לפעמים “הלמה של אוגדן” - כך היא מופיעה בספר האוטומטים של הופקרופט ושות’, שהוא כנראה הספר הידוע ביותר על הנושא כיום, וכך היא מופיעה גם בויקיפדיה האנגלית (כנראה בעקבות הופקרופט). אבל הניסוח במאמר המקורי של אוגדן היה שונה וחזק יותר והוא זה שאציג עכשיו (הסיבה לכך היא שאוגדן הוכיח את הלמה שלו כדי להוכיח את עניין רב המשמעות שאגיע אליו בסוף הפוסט; עד כמה שאני רואה, בניסוח של הופקרופט ושות’ אי אפשר לעשות את זה, והם אפילו לא מנסים אלא סתם מזכירים את הלמה בתוך תרגיל כבדרך אגב). הטענה של אוגדן היא כזו: אם \( L \) היא חסרת הקשר, אז קיים \( n \) טבעי כך שלכל מילה \( z\in L \) וסימון של לפחות \( n \) תווים ב-\( z \), קיים ל-\( z \) פירוק \( z=uvwxy \) כך שמתקיים \( uv^{i}wx^{i}y\in L \) כרגיל לכל \( i\ge0 \), אבל התכונות של הפירוק יותר מורכבות: ראשית, \( w \) מכיל לפחות תו מסומן אחד; שנית, או שגם \( u \) וגם \( v \) מכילים תו מסומן, או שגם \( x \) וגם \( y \) מכילים תו מסומן. לבסוף, כרגיל, \( vwx \) לא מכיל יותר מ-\( n \) תווים מסומנים.

הניסוח הזה שונה ממה שראינו עד כה בכך שיש דרישה כלשהי על \( u,w,y \) - החלקים ש”לא מנפחים” - ב-\( w \) מובטח לנו שיהיה תו מסומן, ואילו ב-\( u,y \) מובטח לנו שלאחד מהם יהיה תו מסומן (וכך גם לחלק שכן מנפחים שנמצא יחד איתו). עוד מעט נראה למה הניסוח הזה מועיל כל כך, אבל לעת עתה בואו נבין איך מוכיחים אותו. ההוכחה אמנם היא בעלת אותו רעיון כמו למת הניפוח, אבל הטיעונים זהירים יותר.

כמקודם, נרצה למצוא מסלול ארוך מספיק בעץ הגזירה, עם משתנה \( A \) שמופיע עליו פעמיים. אבל אנחנו צריכים להקפיד שתת-עץ הגזירה של \( A \) הזה יכיל מספיק תווים מסומנים. צמתים “מוצלחים” בהיבט הזה הם צמתים שבתת-העץ של כל אחד משני הבנים שלהם יש תווים מסומנים - אוגדן קורא להם “צמתי \( B \)”. עכשיו אוגדן בוחר בתוך המסלול שלו מסלול בעץ שיש בו מספר מקסימלי של צמתי \( B \), ושמסתיים בתו מסומן (הסיום של המסלול יהיה בתוך ה-\( w \) שלנו, ולכן הדרישה הזו תבטיח שב-\( w \) יהיה תו מסומן). עכשיו, מה שאוגדן רוצה כדי שהלמה תעבוד הוא שבמסלול שלו יהיו לפחות \( 2\left|V\right|+3 \) צמתי \( B \) - זה משמעותית יותר גדול מאשר ה-\( \left|V\right|+1 \) שרצינו עבור למת הניפוח הרגילה, ולכן הבחירה של \( n \) תהיה גדולה יותר - \( n=2^{2\left|V\right|+3} \). הטיעון שמסביר למה עבור \( n \) כזה בהכרח יש לנו מספיק צמתי \( B \) דומה לטיעון הרגיל בלמה, כשלא היו צמתים מסומנים בכלל; הרעיון הוא שרק צומת \( B \) יגדיל את מספר התווים המסומנים במילה הסופית, בזמן שצומת שרק לאחד משני בניו יש תווים מסומנים לא הולך להגדיל את מספר התווים המסומנים הכולל. נסו להוכיח זאת לעצמכם אם אתם לא משוכנעים.

עכשיו החלק הטריקי. אנחנו רוצים להבטיח שיהיו מקומות מסומנים גם ב-\( u,v \) או \( x,y \). בואו ניקח צומת \( B \) שהבן הימני שלו ממשיך על גבי המסלול שבחרנו - מה קורה עם הבן השמאלי שלו? לבן השמאלי הזה יהיה תת-עץ שמכיל תו מסומן, והוא בא לפני תת-העץ של הבן השמאלי של הצומת. כלומר, אם הצומת גבוה מספיק, התו המסומן הזה יהיה בתוך משהו שבא לפני \( w \).

אז הנה מה שנעשה. נחלק את צמתי ה-\( B \) על המסלול שלנו לשתי קבוצות, \( C_{L} \) ו-\( C_{R} \), כך שכל צמתי ה-\( B \) ב-\( C_{L} \) הם כאלו שהבן הימני שלהם ממשיך על המסלול, ועבור הצמתים ב-\( C_{R} \) הבן השמאלי ממשיך על המסלול. מכיוון שהיו \( 2\left|V\right|+3 \) צמתי \( B \) במסלול, בהכרח אחת משתי הקבוצות הללו כוללת לפחות \( \left|V\right|+2 \) צמתים - בואו נניח שזו \( C_{L} \). ניקח את הצומת הראשון ב-\( C_{L} \) ונסמן אותו ב-\( D \)- הצומת הזה הולך ליצור תו מסומן בתוך \( u \) עם הבן השמאלי שלו. עכשיו נשארו לנו \( \left|V\right|+1 \) צמתים ב-\( C_{L} \) על המסלול, שכולם באים אחרי \( D \), אז ניקח כמו קודם משתנה \( A \) שמופיע פעמיים ועושה את זה הכי נמוך שרק אפשר. המשתנה הזה שייך ל-\( C_{L} \), ולכן הבן השמאלי של המופע הראשון שלו הולך ליצור תו מסומן אחד לפחות - התו הזה יהיה ב-\( v \). קיבלנו את מה שרצינו, במחיר של ניתוח עדין יותר של הלמה, ובחירה של \( n \) גדול יותר.

אני רק רוצה לחדד עוד נקודה עדינה - בניסוח הלמה שלו, אוגדן לא אומר רק ש-\( uv^{i}wx^{i}y\in L \) לכל \( i\ge0 \) - הוא אומר במפורש שקיים משתנה \( A \) כך ש-\( S\Rightarrow^{*}uAy\Rightarrow^{*}uvAxy\Rightarrow^{*}uvwxy \). זה יהיה לנו חשוב בהמשך.

כדי להראות למה זה שימושי, בואו נדבר על רב-משמעות. כזכור, דקדוק הוא רב משמעי אם קיימת מילה אחת לפחות שיש לה שני עצי גזירה שונים. כלומר, יש שתי דרכים שונות לגזור אותה, שנבדלות לא רק בשאלה מתי מופעל כלל גזירה על משתנה, אלא גם איזה כלל גזירה הופעל. לדוגמה, שתי הגזירות \( A\Rightarrow BC\Rightarrow bC\Rightarrow bc \) ו-\( A\Rightarrow BC\Rightarrow Bc\Rightarrow bc \) מתאימות לאותו עץ גזירה ונבדלות רק בסדר שבו בוצעו הגזירות של המשתנים; לעומת זאת \( A\Rightarrow BC\Rightarrow bbC\Rightarrow bbb \) ו-\( A\Rightarrow BC\Rightarrow Bbb\Rightarrow bbb \) הן גזירות שמתאימות לעצי גזירה שונים (בראשון \( B \) גוזר שני \( b \)-ים, ובשני דווקא \( C \) גוזר שני \( b \)-ים). לכן דקדוק שמאפשר את הגזירות מהדוגמה השניה הוא רב משמעי.

רב משמעות היא עניין בעייתי כאשר אנחנו רוצים להשתמש בעץ הגזירה של מילה כדי להבין את המבנה שלה - למשל, להשתמש בעץ הגזירה של תוכנית מחשב כדי להבין את מבנה התוכנית, ואנחנו מן הסתם לא רוצים לאפשר שתי משמעויות שונות (ועצי גזירה שונים לאותה תוכנית מחשב אכן יובילו לרוב לשתי תוכניות שמתנהגות בצורה שונה - די אסון). זה מעלה מייד שתי שאלות - ראשית, בהינתן דקדוק, האם ניתן לבדוק האם הוא רב משמעי? ושנית, בהינתן דקדוק, האם ניתן להמיר אותו בדקדוק אחר עבור אותה שפה, שהוא כן חד משמעי?

באופן די עגום, התשובה לשתי השאלות הללו היא “לא”, או ליתר דיוק, “לא תמיד”. לא אסביר כרגע למה לא תמיד ניתן לבדוק האם דקדוק נתון הוא רב משמעי, אבל אגיע לזה בהמשך; עכשיו אסביר למה לא תמיד ניתן להמיר דקדוק רב משמעי בדקדוק חד משמעי - זה בגלל שיש שפות שהן רב משמעיות טבועות, דהיינו כל דקדוק עבורן יהיה בהכרח רב משמעי. והן לא חייבות להיות מסובכות; הדוגמה שלי היא השפה התמימה למראה \( L=\left\{ a^{n}b^{n}c^{k}\ |\ n,k\in\mathbb{N}\right\} \cup\left\{ a^{k}b^{n}c^{n}\ |\ n,k\in\mathbb{N}\right\} \). כלומר, אוסף כל המילים מהצורה \( a^{*}b^{*}c^{*} \) כך שמספר ה-\( b \)-ים שווה למספר ה-\( a \)-ים או למספר ה-\( c \)-ים. ברור שזו שפה חסרת הקשר כי תחשבו על אוטומט מחסנית שמקבל אותה: הוא מחליט אי דטרמיניסטית מראש למי מספר ה-\( b \)-ים יהיה שווה ואז מתנהג כמו אוטומט עבור \( \left\{ a^{n}b^{n}\ |\ n\in\mathbb{N}\right\} \) תוך שאת האותיות מהסוג השלישי הוא סתם קורא ולא נוגע במחסנית (תרגיל קל: כתבו דקדוק עבור השפה הזו).

נותר לי להוכיח שהשפה היא רב משמעית טבועה. קחו רגע ותנסו לחשוב איך מוכיחים את זה. ועוד יותר מכך - איך הלמה של אוגדן תהיה קשורה לכך. לי עצמי אין מושג, כשאני כותב את הפוסט; הספקתי כבר לשכוח איך זה עובד, ולכן זה הולך להרגיש לי (שקורא את ההוכחה תוך כדי הכתיבה) כמו קסם בדיוק כמו לכם. כרגע אני לא ממש רואה קשר.

אוקיי, בואו נתחיל (קראתי את ההוכחה - וואו, מגניב!). נניח ש-\( n \) הוא הקבוע שהלמה של אוגדן מבטיחה לנו (וניקח \( n>3 \) כי נזדקק בהמשך לכך ש-\( 2n<n! \)). המילה שאראה שחייבים להיות לה שני עצי גזירה שונים תהיה באופן ממש אינטואיטיבי המילה \( a^{n+n!}b^{n+n!}c^{n+n!} \), כאשר \( n! \) (\( n \) עצרת), כזכור, הוא קיצור ל-\( 1\cdot2\cdots n \) (במבט ראשון זה נראה לא קשור בעליל, אבל עצרת היא מספר שימושי שצץ בהרבה הוכחות בגלל התכונה הנחמדה שלה שהיא מתחלקת בכל מספר מ-1 ועד \( n \)).

כדי להראות את שני עצי הגזירה השונים הללו, ניקח שתי מילים שונות שהן תת-מילים של המילה שלנו, נפעיל עליהן את הלמה של אוגדן ונראה שאפשר “לנפח” אותן כדי לקבל את המילה שלנו, ושני הניפוחים חייבים להיות שונים באופיים ולכן לא יכולים להתאים לאותו עץ גזירה. נתחיל מהמילה \( a^{n}b^{n}c^{n+n!} \). הלמה של אוגדן מבקשת מאיתנו לסמן לפחות \( n \) אותיות, אז בואו נסמן בדיוק את ה-\( a \)-ים במילה. עכשיו קיבלנו פירוק \( uvwxy \) של המילה, שבו \( w \) כולל לפחות אות מסומנת אחת - כלומר, \( w \) מוכל בחלק של ה-\( a \)-ים. לכן גם \( u,v \) שבאות לפני \( w \) מוכלות בחלק של ה-\( a \)-ים (אבל שימו לב - שום דבר לא מונע מ-\( u,v \) להיות שתיהן ריקות; הלמה של אוגדן לא מבטיחה שיהיה בהן משהו).

בואו נבין עכשיו איך \( x \) נראה. הוא בא אחרי \( w \) ולכן יכול להיות בעצם בכל מקום במילה, אבל אם \( x \) יכלול שתי אותיות שונות, \( uv^{2}wx^{2}y \) בהכרח לא תהיה שייכת לשפה (כי השפה כוללת רק מילים שבהן קודם באים כל ה-\( a \)-ים, אחר כך כל ה-\( b \)-ים ובסוף כל ה-\( c \)-ים; אם \( x \) כולל שתי אותיות שונות ונחזור עליו פעמיים, נראה אותיות נעלמות ואז חוזרות שוב). לכן \( x \) מורכב כולו מאחת משלוש האותיות האפשריות (וייתכן שהוא ריק).

עכשיו, בואו נסמן את הגדלים של החלקים המנופחים: \( \left|v\right|=p,\left|x\right|=q \). אז \( p,q\ge0 \) ובנוסף אנחנו יודעים ש-\( 0<p+q\le2n<n! \). כמו כן אפשר עכשיו לכתוב את המבנה של החלקים הללו: \( v=a^{p} \) תמיד, בזמן ש-\( x \) שייך לאחת משלוש צורות אפשריות: \( x=a^{q} \) או \( x=b^{q} \) או \( x=c^{q} \).

עכשיו בואו ונראה מה קורה כשמנפחים את המילה, ונבדיל בין אפשרויות שונות על בסיס הערכים הפוטנציאליים של \( x \).

אם \( x=a^{q} \) אז \( uv^{2}wx^{2}y=a^{n+p+q}b^{n}c^{n+n!} \) וזו בבירור לא מילה בשפה כי מספר ה-\( a \)-ים שונה ממספר ה-\( b \)-ים ששונה ממספר ה-\( c \)-ים. מסקנה: \( x\ne a^{q} \). מכאן אנחנו לומדים משהו קריטי להמשך - \( x \) לא כולל אותיות מסומנות, ולכן \( v \) חייב לכלול כאלו, כלומר \( \left|v\right|=p>0 \).

אם \( x=c^{q} \) אז \( uv^{2}wx^{2}y=a^{n+p}b^{n}c^{n+n!+q} \). כבר ראינו ש-\( p>0 \) ולכן \( n+p\ne n \) ושוב קיבלנו מילה שאינה בשפה.

המסקנה היא שבהכרח \( x=b^{q} \), כדי שיוכל “לאזן” את \( v \): \( uv^{2}wx^{2}y=a^{n+p}b^{n+q}c^{n+n!} \). מכיוון שהמילה הזו חייבת להיות שייכת לשפה (אחרת נגיע לסתירה כללית), בהכרח \( p=q \). זה אומר שכשאנחנו מנפחים את המילה, אנחנו מגדילים את מספר ה-\( a \)-ים וה-\( b \)-ים באותה כמות בדיוק - בואו ננפח עד שנגיע ל-\( n+n! \). כאן השימוש בעצרת משתלם לנו - אנחנו לא יודעים מהו \( p \), אבל אנחנו יודעים ש-\( p\le n \) (כי כבר ראינו ש-\( v \) כלול כולו ב-\( a \)-ים ויש רק \( n \) כאלו) ולכן \( p|n! \), כלומר קיים \( t \) כך ש-\( pt=n! \). וכעת: \( uv^{t+1}wx^{t+1}y=a^{n+pt}b^{n+pt}c^{n+n!}=a^{n+n!}b^{n+n!}c^{n+n!} \). הוכחנו שהדקדוק שלנו יודע לגזור את \( a^{n+n!}b^{n+n!}c^{n+n!} \).

בואו נחדד את מה שראינו, תוך שאנו זוכרים מה אוגדן בדיוק אומר - הוא אומר שקיים משתנה \( A \) כך ש-\( S\Rightarrow^{*}uAy\Rightarrow^{*}uvAxy\Rightarrow^{*}uv^{t+1}Ax^{t+1}y\Rightarrow^{*}uv^{t+1}wx^{t+1}y=a^{n+n!}b^{n+n!}c^{n+n!} \). מה שחשוב כאן הוא ש-\( A \) מייצר את \( v,x \) ולכן גוזר רק את האותיות \( a,b \).

עכשיו אפשר לחזור על כל מה שאמרנו עד כה אבל כשמתחילים מהמילה \( a^{n+n!}b^{n}c^{n} \) שגם כן שייכת לשפה. הלמה של אוגדן תראה לנו בסופו של דבר שקיים משתנה \( A^{\prime} \) כך ש-

\( S\Rightarrow^{*}u^{\prime}A^{\prime}y^{\prime}\Rightarrow^{*}u^{\prime}v^{\prime}A^{\prime}x^{\prime}y^{\prime}\Rightarrow^{*}u^{\prime}\left(v^{\prime}\right)^{t+1}A^{\prime}\left(x^{\prime}\right)^{t+1}y^{\prime}\Rightarrow^{*}u^{\prime}\left(v^{\prime}\right)^{t+1}w^{\prime}\left(x^{\prime}\right)^{t+1}y^{\prime}=a^{n+n!}b^{n+n!}c^{n+n!} \)

רק שהפעם יצא ש-\( A^{\prime} \) גוזר רק \( b \)-ים ו-\( c \)-ים.

קיבלנו שתי גזירות של \( a^{n+n!}b^{n+n!}c^{n+n!} \) בדקדוק שלנו. אבל האם הן באמת מתאימות לעצי גזירה שונים? אינטואיטיבית כנראה כבר ברור שכן כי איכשהו \( A \) ו-\( A^{\prime} \) לא מסתדרים לנו טוב ביחד, אבל צריך לתת פה נימוק פורמלי יותר. ראשית נשים לב לכך ש-\( A \) לא יודעת לגזור את \( A^{\prime} \) וגם ההפך נכון (כי \( A \) גוזרת רק \( a,b \) בעץ הגזירה שלה, ולכן אם \( A^{\prime} \) הייתה בעץ הגזירה, אז היו גם \( c \)-ים בפנים). זה אומר שאם שתי הגזירות שלעיל הן גזירה אחת, אז על ידי כך שנבצע את הגזירה הזו אבל “נתאפק” ולא נגזור לא את \( A \) ולא את \( A^{\prime} \) אחרי שהן מופיעות לראשונה, נקבל את הדבר הבא: \( S\Rightarrow^{*}t_{1}At_{2}A^{\prime}t_{3} \). עכשיו אני יכול להמשיך ולגזור את \( A,A^{\prime} \) כמה פעמים שנרצה לפני שנגזור אותן ל-\( w,w^{\prime} \) - בואו נגזור את \( A \) במשך \( i \) פעמים ואת \( A^{\prime} \) במשך \( j \) פעמים, עבור \( i,j \) שמשתלמים לנו (נראה עוד מעט מה זה אומר). נקבל את המילה הבאה, ששייכת כמובן לשפה \( L \) כי היא נגזרה על ידי הדקדוק:

\( t_{1}v^{i}wx^{i}t_{2}\left(v^{\prime}\right)^{j}w^{\prime}\left(x^{\prime}\right)^{j}t_{3} \)

מה שאני רוצה לומר הוא שעבור \( i,j \) גדולים מספיק, מספר ה-\( b \)-ים במילה הזו בהכרח יהיה גדול ממספר ה-\( a \)-ים וגם ממספר ה-\( c \)-ים, ולכן המילה לא תהיה שייכת לשפה. כדי לראות את זה, בואו נחשב כמה אותיות מכל סוג יש במילה הזו. לא נוכל לדעת במדויק, אבל נוכל לקבל חסם. למשל, אנחנו יודעים שהמקום שבו ה-\( a \)-ים נגמרים הוא לכל היותר בתוך \( w \), כי כבר ראינו ש-\( x \) חייב להכיל רק \( b \)-ים. לכן מספר ה-\( a \)-ים במילה חסום מלמעלה על ידי \( \left|t_{1}\right|+i\left|v\right|+\left|w\right| \). באופן דומה, מספר ה-\( c \)-ים במילה חסום מלמעלה על ידי \( \left|t_{3}\right|+j\left|x^{\prime}\right|+\left|w^{\prime}\right| \). לעומת זאת, את מספר ה-\( b \)-ים במילה אני יכול לחסום מלמטה: אני יודע שלכל הפחות כל \( x \) הוא \( b \)-ים, ושכל \( v^{\prime} \) הוא \( b \)-ים, ולכן גם \( t_{2} \) שכלוא בין שניהם חייב להיות כולו \( b \)-ים, ולכן קיבלנו שמספר ה-\( b \)-ים הוא לפחות \( i\left|x\right|+\left|t_{2}\right|+j\left|v^{\prime}\right| \). ואני יודע גם קצת יותר מזה - אני יודע ש-\( \left|x\right|=\left|v\right| \) וש-\( \left|v^{\prime}\right|=\left|x^{\prime}\right| \).

יש כאן כבר יותר מדי אותיות ותגים וסימונים, אז בואו נשנה אותם כדי שיהיה יותר קל להבין מה קורה פה. נסמן ב-\( f\left(\sigma\right) \) את מספר המופעים של \( \sigma \). אז יש לנו את המשוואות הבאות:

\( f\left(a\right)\le A+i\alpha \)

\( f\left(c\right)\le C+j\beta \)

\( f\left(b\right)\ge B+i\alpha+j\beta \)

כאשר \( A,B,C,\alpha,\beta \) הם קבועים חיוביים כלשהם. עכשיו הרבה יותר קל לראות מה קורה פה. כך למשל נניח שאנו רוצים להבטיח ש-\( f\left(a\right)<f\left(b\right) \), כלומר ש-\( A+i\alpha<B+i\alpha+j\beta \); נעביר אגפים ונקבל שצריך להתקיים \( j>\frac{A-B}{\beta} \). באופן דומה כדי שיתקיים \( f\left(c\right)<f\left(b\right) \) צריך להתקיים \( i>\frac{C-B}{\alpha} \). שימו לב שהחסמים הללו על הערכים של \( i,j \) לא תלויים זה בזה, כך שאין לנו בעיה לבחור ערכים מספיק גדולים עבור שניהם, מה שיסיים את ההוכחה - הראינו שאם אין למילה שלנו שני עצי גזירה שונים אלא עץ גזירה יחיד, אז אפשר לנצל את עץ הגזירה הזה כדי לגזור מילה אחרת שהיא בבירור לא בשפה. זה מסיים את ההוכחה כולה.

אני מקווה שלא כולם הלכו לאיבוד בים הפרטים הטכניים. הם לא היו נוראיים כל כך, לדעתי; אולי בגלל שאני כותב את הפוסט ולכן מוכרח להרגיש “בידיים” מה הולך שם (בקריאה נטו של פרטים טכניים תמיד יותר קל ללכת לאיבוד). התוצאה אינה כה מסובכת מבחינה רעיונית - בעזרת הלמה של אוגדן יש לנו שליטה רבה יותר על האופן שבו מילים מנופחות, וכדי להראות שלא קיים דקדוק חד משמעי אנחנו מייצרים את אותה מילה בשתי דרכים שונות מהותית על ידי ניפוחים שונים של מילים פשוטות יותר. לטעמי זו הייתה תוצאה יפה מאוד.

נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: