על משחקים ומספרים (חלק א': משחקים. וקצת מספרים)

בראשית ימי הבלוג, חלק מהפוסטים הראשונים שפרסמתי עסקו או בתורת המשחקים, או בבנייה השיטתית של מערכות המספרים המרכזיות במתמטיקה (הטבעיים, השלמים, הרציונליים, הממשיים והמרוכבים). אני רוצה עכשיו לחזור לנושאים הללו באופן שאיכשהו מצליח לחבר את שניהם, בהתבסס על שני ספרים שכתב המתמטיקאי ג’ון קונווי - הראשון, On Numbers and Games, והשני (שאותו כתב עם עוד אנשים), Winning Ways for your Mathematical Plays. בשני הספרים הללו יש ניתוחים של סוגים מסויימים של משחקים לשני שחקנים, ומה שכל כך יפה בזה הוא שבאופן טבעי למדי, מהניתוחים הללו צצה לה מערכת מספרים יפה ומעניינת במיוחד, שאבריה מכונים לפעמים (לא על ידי קונווי בספרים אלו) “מספרים סוריאליסטיים”. מערכת המספרים הזו כוללת בתוכה את המספרים הממשיים, אבל גם איברים נוספים - למשל, את כל המספרים הסודרים. אבל יותר מזה - גם הופכיים עבור המספרים הסודרים, שזה כבר בוודאי נשמע מוזר לחלקכם, ועוד כל מני דברים מעניינים. מה שבאמת יפה הוא שהמערכת הזו מתקבלת על ידי הגדרה פשוטה ביותר, שאציג מייד עכשיו כדי לא לעשות טיזינג מיותר:

אם \( L,R \) הן שתי קבוצות של מספרים כך שאין איבר של \( L \) הגדול או שווה לאיבר של \( R \) אז \( \left\{ L|R\right\} \) הוא מספר. כל המספרים נבנים בצורה זו.

זו ההגדרה, אבל מה הולך כאן? למה אלו מספרים? איך מקבלים פה מספרים ממשיים? איך מקבלים את \( \pi \)? מה זו השטות הזו שיש לסודרים הופכי? מה למען ג’ון פון-נוימן הקשר למשחקים? הרבה שאלות, ואענה על כולן. יהיה כיף; זה נושא שחביב עלי מאוד ואני בטוח שגם אלו מכם שלא מכירים הרבה מתמטיקה יוכלו ליהנות ממנו. כמובן, אני הולך לחפף; אני ממליץ על קריאת הספרים למי שלא יהיה מרוצה מהדילוגים שלי (מבין שניהם, On Numbers and Games הוא המתמטי-פורמלי יותר, לטוב ולרע, אבל גם הוא כתוב בצורה קלילה יחסית).

בואו נתחיל מלדבר על משחקים. משחק, אצלנו, תמיד יהיה משחק לשני שחקנים, שאקרא להם אליס ובוב או שמאל וימין (אליס תהיה שמאל, בוב יהיה ימין, ונהיה לטובת אליס). אנחנו מניחים שבמשחק יש ידיעה שלמה - אין מידע חסוי (כמו שיש למשל ב”צוללות”) או אלמנטים אקראיים (כמו הטלות קוביה בשש-בש, שאפשר לחשוב עליהן בתור סוג של מידע חסוי). עד כאן סטנדרטי, ומוביל למשחקים שנקראים “משחקים דמויי-שחמט”. אבל אנחנו מגבילים את עצמנו עוד יותר - אין תוצאות תיקו, והמשחקים תמיד מתנהלים באופן הבא: אחד השחקנים מבצע מהלך, ואז השחקן השני מבצע מהלך, וכן הלאה לסירוגין, עד אשר שחקן כלשהו לא יכול לבצע מהלך חוקי כלשהו ואז הוא מפסיד. דבר כזה לא קורה בשחמט. בשחמט, שחקן מפסיד אם המלך שלו מאויים ואין לו דרך להגן עליו; בהחלט ייתכן שתהיה סיטואציה שבה שחקן כלשהו לא יכול לבצע אף מהלך חוקי אבל לא להפסיד - אם כל מהלך שהשחקן יבצע יגרום למלך שלו להיות מאויים, אסור לו לבצע אף מהלך. לסיטואציה הזו קוראים “פט” והיא נחשבת לתיקו. כך שאנחנו רואים שהוצאנו את שחמט מהמשחק. אל תדאגו, יש עוד מספיק משחקים מעניינים לדבר עליהם.

ההנחה האחרונה שלנו היא שהמשחקים הם סופיים - כלומר, שתמיד אחרי מספר סופי של מהלכים המשחק יסתיים בניצחון של אחד השחקנים. זה לא אומר שמספר המהלכים החוקיים של כל שחקן בכל שלב חייב להיות סופי; בהחלט ייתכנו משחקים שבהם יש סיטוצאיות שבהם השחקנים יכולים לבצע אינסוף מהלכים.

בבלוג כבר דיברתי על מספר משחקים שמתאימים לכל הדרישות הללו - נים וצ'ומפ הן שתי דוגמאות (צריך קצת להיזהר עם ההגדרה של מתי אין יותר פעולה חוקית). עם זאת, אני לא אדבר על המשחקים הללו (לפחות לא כרגע) כי הם מסובכים מדי. בשלב הראשון אני רוצה להראות איך ניתוח של משחקים מוביל להגדרה של מספרים סוריאליסטיים, אבל בניתוח של משחק כמו נים יווצרו עוד כל מני דברים שאינם מספרים בכלל. לכן אני בוחר להתחיל ממשחק שאולי נראה קצת מוזר במבט ראשון אבל הוא מתאים בול בתור מבוא לנושא (ולכן הוא מה שמופיע ראשון גם ב-Winning Ways) - הקנבוש (Hackenbush).

“לוח המשחק” בהקנבוש הוא ציור שכולל “קרקע” בצבע ירוק, ועוד כל מני קווים בצבעי אדום וכחול (“קו” אצלנו הוא קו ישר - אם הקו “נשבר” לשני חלקים בזוויות שונות, אלו שני קווים שונים מבחינתנו). מכל קו אפשר להגיע דרך קווים אחרים אל הקרקע - אין קו “מנותק”. המשחק מתנהל כך: אליס בתורה בוחרת קו אדום כלשהו ומוחקת אותו מהלוח. בוב, בדומה, בוחר קו כחול ומוחק מהלוח. אם מחיקת קו כזו גרמה לניתוק של חלק מהקווים מן הקרקע, כל הקווים המנותקים נמחקים. אליס מפסידה אם תורה לשחק ולא נותרו קווים אדומים, ובוב מפסיד אם תורו ולא נותרו קווים כחולים. הנה לוח לדוגמא:

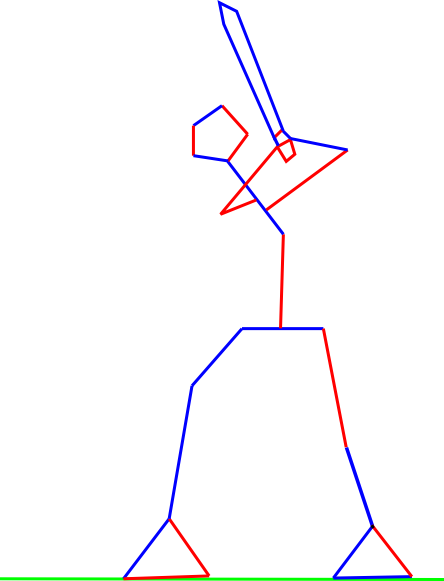בפועל יותר נוח לדבר על גרף מאשר על “ציור” - ובכן, לוח הקנבוש הוא גרף שבו הקשתות צבועות באדום וכחול, וחלק מהצמתים מסומנים כ”מחוברים לקרקע”, ואפשר למחוק קשתות, ואחרי מחיקת קשת מוחקים את כל הצמתים שהפכו למנותקים מהקרקע ואת כל הקשתות שמחוברות אליהם.

מה שנחמד בהקנבוש הוא שניתן לכל לוח משחק להתאים מספר שאומר לאיזה שחקן יש יתרון. אם המספר יהיה חיובי אז היתרון יהיה של אליס, אם הוא יהיה שלילי היתרון יהיה של בוב, ואם הוא יהיה 0 זה אומר שמי שמתחיל, מפסיד (כלומר, היתרון הוא אצל השחקן שלא מתחיל). מה שעוד יותר נחמד הוא שהיתרון הזה לאו דווקא יהיה מספר שלם, ושעוד מעט נבין גם את ההגיון שמאחורי זה.

אני אאמץ את שיטת הסימון הבאה לתיאור לוח הקנבוש: אני אכתוב אותו בתור \( \left\{ L|R\right\} \) כאשר \( L \) תהיה רשימת הלוחות שיכולים להתקבל מהלוח הנוכחי אחרי מהלך שאליס תבצע, ואילו \( R \) תהיה רשימת הלוחות שיכולים להתקבל מהנוכחי אחרי מהלך שבוב יבצע. בואו נתחיל מהסיטואציה הכי פשוטה: לוח ריק. מה שאני אצייר רק בתור קו ירוק ותו לא. במקרה הזה, אין לא לאליס ולא לבוב מהלכים חוקיים, כלומר המצב הוא \( \left\{ \ |\ \right\} \). מי מבין השניים שמתחיל, מפסיד מייד כי אין לו מה לעשות, ואז השני מנצח. לכן אסמן \( \left\{ \ |\ \right\} =0 \) (זוהי הגדרה של 0, אם תרצו).

נתבונן כעת על לוח שכולל קו אדום יחיד ותו לא:

אם אליס מתחילה לשחק, אז המהלך היחיד שלה הוא למחוק את הקו האדום, מה שמעביר אותנו ללוח ריק שאנחנו כבר מכירים - זה 0. לעומת זאת, אם בוב מתחיל לשחק אין לו מהלכים חוקיים בכלל והוא מייד מפסיד. לכן אסמן את הלוח הזה ב-\( \left\{ 0|\ \right\} \). אינטואיטיבית, אליס מובילה כאן על בוב במהלך אחד (כי יש לה קו אחד יותר מאשר יש לו) ולכן נסמן \( \left\{ 0|\ \right\} =1 \). באופן דומה, הלוח שבו יש קו יחיד שהוא כחול מתאים לסימון \( \left\{ \ |0\right\} \), ומכיוון שהוא מתאר יתרון של מהלך אחד של בוב על אליס, נסמן אותו במספר שלילי (כלומר, אליס בחיסרון של מהלך אחד מול בוב), כלומר \( \left\{ \ |0\right\} =-1 \).

קל לנחש איך אפשר להמשיך מכאן: לוח שבו יש \( n \) קווים אדומים (שכולם מחוברים לקרקע) ואף קו כחול מתאים ל-\( \left\{ n-1|\ \right\} =n \) ולוח שבו יש \( n \) קווים כחולים ואף קו אדום מתאים ל-\( \left\{ \ |-\left(n-1\right)\right\} =-n \). כבר קיבלנו את כל המספרים השלמים, אבל עד כה טרם ראינו משהו מתוחכם.

בואו נסתכל עכשיו על לוח שבו יש קו אדום וקו כחול אחד, ששניהם מחוברים לקרקע:

הלוח הזה מתאים ל-\( \left\{ -1|1\right\} \), כי המהלך היחיד של אליס ישאיר קו כחול יחיד, והמהלך היחיד של בוב ישאיר קו אדום יחיד, ואת שתי הסיטואציות הללו כבר ניתחנו ונתנו להן שמות. המשחק הזה הוא עוד דוגמה למשחק שבו המתחיל מפסיד, מה שקראנו לו 0. כלומר, אני רוצה לסמן \( \left\{ -1|1\right\} =0 \). מצד שני, הסימון \( 0 \) כבר שמור ללוח אחר, \( \left\{ \ |\ \right\} \). אלו שני לוחות שונים, אבל בשורה התחתונה המשחק שהם מגדירים הוא זהה באספקט שמעניין אותנו, שהוא מה גודל היתרון שיש לשחקן אחד על פני השני. לכן אפשר לומר ש-\( \left\{ \ |\ \right\} \) ו-\( \left\{ -1|1\right\} \) הם שני ייצוגים שונים של אותו מספר ולהתייחס אליהם כשווים. למי שנפנוף הידיים הזה מפריע לו - אל דאגה, בהמשך ניתן הגדרה פורמלית של השוויון הזה.

דרך מעניינת אחרת לחשוב על המשחק הזה הוא בתור שני משחקים נפרדים שבמקרה יושבים אחד ליד השני:

באופן כללי אפשר לחשוב על “הרכבה” של משחק מתוך כמה משחקים בלתי תלויים זה בזה, כשהחוקים הם המתבקשים: כל שחקן, בתורו, בוחר את אחד מלוחות המשחק ומבצע צעד אחד באותו לוח. מפסיד השחקן שבתורו לא יכול לבצע מהלך באף לוח. כעת מתבקש להגדיר חיבור של משחקים בתור “המשחק שמתקבל מההרכבה הזו”. במקרה שלנו, נקבל ש-\( 1+\left(-1\right)=0 \) - לא מפתיע! (ושוב, לא לדאוג, הגדרות פורמליות יגיעו בהמשך).

עכשיו בואו נעבור למשהו שונה ממה שראינו עד כה: לוח שבו יש קו אדום אחד שמחובר לקרקע, ומעליו יש קו כחול:

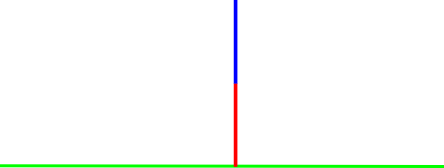כאן בבירור זה משחק “אטומי” שלא ניתן לפרק לתת-משחקים פשוטים יותר שאחר כך מחברים, כי שני הקווים הם לא בלתי תלויים זה בזה - אם אליס תסיר את הקו האדום, אז היא תגרום גם למחיקת הקו הכחול, ובוב יפסיד. לכן המהלך היחיד של אליס מעביר את הלוח למצב 0, בעוד המהלך היחיד של בוב מעביר את הלוח למצב 1 (קו אדום בודד לאליס). כלומר, המשחק הזה הוא \( \left\{ 0|1\right\} \). לאיזה ערך מספרי הוא מתאים?

בבירור הערך המספרי הזה צריך להיות חיובי, הרי לאליס יש יתרון במשחק הזה. אבל כמה גדול היתרון? האם זה יתרון של מהלך אחד, כמו שהיה במשחק שבו לאליס היה קו אדום יחיד ולבוב כלום (או, למשל, שני קווים אדומים לאליס וקו כחול אחד לבוב)? ובכן, לא, זה יתרון קטן יותר, כי בכל זאת אם בוב מתחיל הפעם הוא יצליח לשרוד עד שלאליס לא יישארו קווים בעצמה (בעוד שבמשחק עם יתרון 1, הוא ישרוד רק עד שלאליס יישאר קו אחד). אז כמה? אני טוען שהיתרון הוא בדיוק \( \frac{1}{2} \), כלומר ש-\( \left\{ 0|1\right\} =\frac{1}{2} \). אבל איך להוכיח דבר כזה?

ובכן, \( \frac{1}{2}+\frac{1}{2}=1 \), או בניסוח אחר \( \frac{1}{2}+\frac{1}{2}+\left(-1\right)=0 \). יותר מכך: אם \( x \) הוא מספר ממשי כלשהו כך ש-\( x+x+\left(-1\right)=0 \) אז נובע מכך ש-\( x=\frac{1}{2} \). אז כדי להוכיח ש-\( \left\{ 0|1\right\} =\frac{1}{2} \) (בהנחה - שלא הוכחתי - שאכן המשחק הזה מתואר על ידי מספר ממשי) די לי להוכיח ש-\( \left\{ 0|1\right\} +\left\{ 0|1\right\} +\left\{ \ |0\right\} =0 \) - כלומר, שהמשחק הבא:

הוא כזה שבו מי שמתחיל, מפסיד (בפרט, שנדרשים שני עותקים של \( \left\{ 0|1\right\} \) כדי “לקזז” את \( \left\{ \ |0\right\} \)).

כדי לראות שמי שמתחיל במשחק מפסיד, בואו פשוט נחשוב איך משחק כזה יתנהל. נניח שאליס מתחילה. היא חייבת לקחת את אחד משני הקווים האדומים שלה. בוב יקח את הכחול שמעל הקו האדום השני. אליס תיקח את האדום האחרון שלה. בוב יקח את הכחול האחרון שלו. הופס! אליס הפסידה.

נניח שבוב מתחיל: אם הוא לוקח את הכחול המבודד שלו, אז אליס לוקחת אדום ומעבירה את המשחק למצב \( \left\{ 0|1\right\} \) שבו בוב תמיד מפסיד. אם כן, לא שווה לבוב לקחת את הכחול המבודד שלו. הוא ייקח את הכחול שמעל אחד מהקווים האדומים, אבל אז אליס תיקח את הקו האדום השני ותשאיר לבוב רק את הכחול המבודד שלו. הוא ייקח אותו, אליס תיקח את האדום השני שלה והופס! בוב הפסיד.

אם כן, \( \left\{ 0|1\right\} =\frac{1}{2} \). רוצים לנחש למה יהיה שווה \( \left\{ 0|\frac{1}{2}\right\} \)? מן הסתם \( \frac{1}{4} \) נראה כמו בחירה הגיונית. לשם כך צריך להראות ש-\( \left\{ 0|\frac{1}{2}\right\} +\left\{ 0|\frac{1}{2}\right\} +\left\{ 0|1\right\} =0 \). נסו לשחק את המשחק ולראות מה קורה.

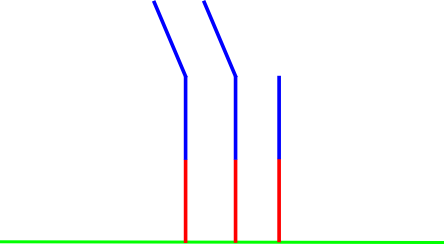שימו לב ללוח שמייצג את \( \left\{ 0|\frac{1}{2}\right\} \): קו אדום, ומעליו שני קווים כחולים. אם נדקדק בהגדרה הפורמלית, הלוח הזה הוא בעצם \( \left\{ 0|\frac{1}{2},1\right\} \): לאליס יש רק אפשרות אחת, של סילוק הקו האדום; בעוד שלבוב יש שתי אפשרויות, לסלק את הקו הכחול העליון (ולעבור אל \( \frac{1}{2} \) או את הקו הכחול התחתון (ולעבור ל-1), אבל שוב - נראה עוד מעט ש-\( \left\{ 0|\frac{1}{2},1\right\} =\left\{ 0|\frac{1}{2}\right\} \).

עכשיו כבר ברור שעל ידי הוספה של עוד ועוד קווים כחולים למעלה נוכל לקבל גם את \( \frac{1}{8} \), ואת \( \frac{1}{16} \), וכן הלאה וכן הלאה - כל שבר מהצורה \( \frac{1}{2^{n}} \). זה מוביל אותנו בצורה טבעית לשתי שאלות: ראשית, מה קורה אם מוסיפים למעלה לא רק קווים כחולים אלא גם אדומים? ושנית, האם אפשר לקבל איכשהו שברים עם מכנה שאינו חזקה של 2?

נתחיל מהשאלה הראשונה עם הלוח הזה:

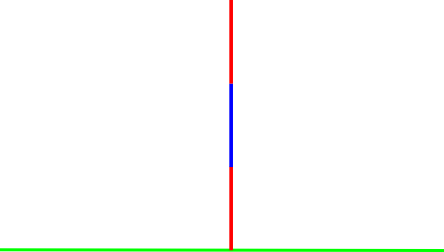מה המהלכים האפשריים בלוח? אליס יכול להעיף את הקו התחתון, ולהישאר עם 0, או להעיף את הקו העליון ולהישאר עם \( \frac{1}{2} \). בוב יכול להעיף רק את הקו האמצעי ולהישאר עם \( 1 \). כלומר, אנחנו ב-\( \left\{ 0,\frac{1}{2}|1\right\} \). אם כבר יש לכם אינטואיציה לא רעה לגבי מה שהולך כאן, כנראה תנחשו שהמצב הזה שווה ל-\( \left\{ \frac{1}{2}|1\right\} =\frac{3}{4} \). כלומר, לא נראה שנקבל משהו ממש חדש מהוספה של קווים אדומים על כחולים על אדומים על כחולים וכן הלאה. כדי להגיע לשבר עם מכנה שונה מחזקה של 2, למשל \( \frac{1}{3} \), נצטרך משהו שונה לגמרי.

אבל בואו נעזוב את זה לרגע, ונעבור לנסיון להבין את הדקויות של הסימון המוזר שבו אנחנו משתמשים. על פניו, כדי להבין מה המספר שמיוצג על ידי \( \left\{ L|R\right\} \), אנחנו נוקטים בשיטה הבאה: מוצאים את המספר הגדול ביותר ב-\( L \) והקטן ביותר ב-\( R \) ומחשבים את הממוצע החשבוני שלהם. זה המקום הראשון שבו האינטואיציה שלנו לא עובדת - האמת היא שהסיטואציה מסובכת יותר. הנה דוגמה פשוטה: \( \left\{ -1|2\right\} \). לכאורה, המשחק הזה אמור להתאים לערך המספרי \( \frac{1}{2} \), שנמצא באמצע הדרך בין \( -1 \) ובין \( 2 \); אבל אם תחשבו שניה, ברור שהמשחק הזה הוא 0. למה? כי אם אליס מתחילה, המהלך היחיד שלה מעביר את המשחק ל-\( -1 \), שהוא משחק שבו בוב מנצח בודאות; ואם בוב מתחיל, המהלך היחיד שלו מעביר את המשחק ל-\( 2 \), שבו אליס מנצחת בודאות. אז יש לנו משחק שבו מי שמתחיל, מפסיד: כבר אמרנו שזה המשחק 0 (ו-\( \frac{1}{2} \) הוא משחק שבו אליס מנצחת). בקיצור, לא משנה כמה חזק מבחינת אליס המצב שבוב מעביר אליו את המשחק, כל עוד אליס מעבירה את המשחק למצב שהוא מפסיד מבחינתה.

לכן יש לנו כמה שאלות שחייבים לענות עליהן לפני שממשיכים:

1. מתי בעצם ביטוי כמו \( \left\{ L|R\right\} \) מגדיר מספר?
2. איך מגדירים מספר חדש מתוך מספרים קיימים?
3. איך בודקים ששני ביטויים שונים מגדירים את אותו המספר?
4. מה הכלל שמאפשר לנו למצוא את המספר שמתאים לביטוי \( \left\{ L|R\right\} \)?

בואו נשכח לרגע ממשחקים ונעבור להגדרות פורמליות. תשובה לשתי השאלות הראשונות מתקבלת מייד מההגדרה שנתתי בראשית הפוסט, ועכשיו נשחק איתה:

אם \( L,R \) הן שתי קבוצות של מספרים כך שאין איבר של \( L \) הגדול או שווה לאיבר של \( R \) אז \( \left\{ L|R\right\} \) הוא מספר. כל המספרים נבנים בצורה זו.

זו דוגמה להגדרה אינדוקטיבית (או רקורסיבית, מה שבא לכם): אנחנו מתארים איך לבנות מספרים חדשים מתוך מספרים שכבר קיימים. נקודה שחשוב לי להדגיש, לפני שנתחיל להשתמש בה כדי לייצר מספרים, היא שההגדרה הזו עדיין לא מאפשרת לנו לראות ש-0 ו-\( \left\{ -1|1\right\} \) הם אותו מספר; לשם כך נצטרך לתת הגדרה מפורשת של שוויון, שתבוא בהמשך.

עוד דבר שכמובן חסר הוא הגדרה של המושג “גדול” כאן. כדי לתאר אותו, סימון: אם \( x=\left\{ L|R\right\} \) אני משתמש בסימון \( x^{L} \) כדי לתאר “איבר כלשהו מתוך \( L \)” וב-\( x^{R} \) כדי לתאר “איבר כלשהו מתוך \( R \)”. האינטואיציה תהיה תמיד ש-\( x^{R} \) הם מספרים שגדולים מ-\( x \) ואילו \( x^{L} \) הם מספרים שקטנים מ-\( x \) (אבל לא בהכרח כל המספרים הגדולים/קטנים מ-\( x \)). תחת האינטואיציה הזו, מתי \( x\ge y \)? ובכן, אם לא קיים מספר שגדול מ-\( x \) אבל קטן מ-\( y \), ולא קיים מספר שקטן מ-\( y \) אבל גדול מ-\( x \).

פורמלית, נגדיר ש-\( x\ge y \) אם לא קיים \( x^{R}\le y \) ולא קיים \( x\le y^{L} \). גם זו הגדרה אינדוקטיבית, אבל נראה שהכל יסתדר לנו. באופן מתבקש נגדיר שוויון של מספרים על פי ההגדרה הזו: \( x=y \) אם \( x\le y \) וגם \( y\le x \).

אם כן, איך אפשר “לעבוד” עם ההגדרה כדי לייצר מספרים? ההתחלה נראית קשה - הרי אין לנו שום מספר שהוגדר עד כה, מאיפה נתחיל? ובכן, מהמצב שבו \( L=R=\emptyset \) - שתי הקבוצות ריקות. מכיוון ששתי הקבוצות ריקות, התנאי של “אין איבר של \( L \) הגדול או שווה לאיבר של \( R \)” מתקיים באופן ריק, וקיבלנו מספר, שאנו מסמנים \( 0=\left\{ \ |\ \right\} \).

מה עכשיו? אפשר “לשתול” את 0 הזה בתוך אגף ימין או שמאל, אבל לא שניהם: \( \left\{ 0|0\right\} \) הוא לא מספר, כי \( 0\le0 \) (בדקו זאת!). לכן אנחנו יכולים לבנות רק שני מספרים חדשים בינתיים: \( \left\{ \ |0\right\} \) ו-\( \left\{ 0|\ \right\} \), שנסמן \( -1 \) ו-\( 1 \), בהתאמה. העובדה שהם מספרים נובעת מכך שתנאי ה-“אין איבר של \( L \) הגדול או שווה לאיבר של \( R \)” עדיין מתקיים באופן ריק. עכשיו בואו ננסה להבין מי גדול ממי.

ראשית, לא ייתכן ש-\( \left\{ \ |0\right\} \ge0 \) כי קיים באגף ימין של \( \left\{ \ |0\right\} \) איבר 0 כך ש-\( 0\le0 \). ההפך כן עובד, ולכן אנחנו מקבלים ש-\( -1\le0 \). באופן סימטרי מקבלים ש-\( 0\le1 \). כמו כן מקבלים בקלות ש-\( -1\le1 \) על ידי בדיקה ישירה, בלי הסתמכות על טרנזיטיביות או משהו דומה.

נמשיך ונגדיר \( 2=\left\{ 1|\ \right\} \). עכשיו מעניין לבדוק האם \( 1\ge2 \) מתקיים. בואו נעשה את זה פורמלית. אני שואל את עצמי שתי שאלות. ראשית, האם קיים \( 1^{R}\le2 \)? לא, מכיוון שה-\( R \) של 1 הוא קבוצה ריקה. שנית, האם קיים \( 1\le2^{L} \)? ובכן, כן, כי \( 1 \) הוא איבר מהצורה \( 2^{L} \). מכאן מקבלים שלא מתקיים \( 1\ge2 \).

ומה עם \( 1\le2 \)? כאן הבדיקה הפוכה. ראשית, האם קיים \( 2^{R}\le1 \)? לא, כי \( R \) של 2 ריק. והאם קיים \( 2\le1^{L} \)? לא, כי ב-\( 1^{L} \) יש רק את 0, ולא מתקיים \( 2\le0 \). כדי לראות את זה, צריך לבצע אינדוקטיבית את הבדיקה גם עבור \( 2\le0 \); מכיוון ש-\( 0\le2^{L} \) מתקיים עבור הבחירה של 1 בתוך האיבר מ-\( L \) של 2, מקבלים ש-\( 2\le0 \) לא מתקיים, כנדרש.

כמו שהבנתם, אין מנוס מכל מני בדיקות קטנות וקטנוניות כדי לוודא דברים עם ההגדרות הללו - זה לא באמת שונה ממה שקורה בהגדרות בסיסיות אחרות. מכאן ואילך לא אטרח להוכיח את רוב הטענות שלי, אבל אתם יכולים לבדוק אותן בתור תרגיל.

עכשיו אפשר לראות למה \( \left\{ -1|1\right\} =0 \), כלומר למה יש לנו שני ייצוגים שונים לאותו מספר (או, אם להיות ממש פורמליים, שני מספרים שונים שמתקיים עבורם יחס השווין; אבל זו צורת חשיבה שגויה, כי למשל עבור מספרים רציונליים כולנו מסכימים ש-\( \frac{1}{2} \) ו-\( \frac{2}{4} \) הם שני ייצוגים שונים של אותו מספר). הם פשוט מקיימים \( \left\{ -1|1\right\} \le0 \) (כי הסיכוי היחיד של זה לא להתקיים הוא אם \( -1>0 \)) וגם \( 0\le\left\{ -1|1\right\} \) (כי הסיכוי היחיד של זה לא להתקיים הוא אם \( 0>1 \)). באותו אופן בדיוק מקבלים גם ש-\( \left\{ -1|2\right\} =0 \) ובאופן כללי שאם \( L \) כוללת כולה מספרים קטנים מ-0 ו-\( R \) כולה מספרים גדולים מ-0, אז \( \left\{ L|R\right\} \) הוא 0. זה אמור להיות שכנוע פורמלי עבורכם, אבל האינטואיציה כבר אמורה להיות ברורה לכם בזכות הגישה ה”משחקית” שהצגתי קודם.

קיבלנו את המספרים השלמים. בואו נגדיר חיבור! ההגדרה די אינטואיטיבית: \( x+y\triangleq\left\{ x^{L}+y,x+y^{L}|x^{R}+y,x+y^{R}\right\} \). כמו קודם, צריך קצת עבודת הכנה כדי שאפשר יהיה להתחיל להשתמש בה - למשל, לראות קודם כל ש-\( 0+0=0 \), ואז ש-\( 0+x=x \) לכל מספר \( x \), באופן אינדוקטיבי, וכן הלאה - אבל מהר מאוד אפשר כבר לראות דברים בסגנון \( 1+\left(-1\right)=0 \) ו-\( 1+1=2 \) וכדומה. ועכשיו אפשר להתחיל לדבר על מספרים כמו \( \left\{ 0|1\right\} \) ולהוכיח ש-\( \left\{ 0|1\right\} +\left\{ 0|1\right\} =1 \), מה שנותן לנו הצדקה לסימון \( \left\{ 0|1\right\} =\frac{1}{2} \). שימו לב - כפי שאיימתי, אני מדלג בקלילות מעל ההוכחה הזו, שדווקא דורשת עבודה.

בהינתן חיבור, חיסור מוגדר על ידי חיבור עם הנגדי - כאן הגדרת הנגדי היא פשוטה: \( -x=\left\{ -x^{R}|-x^{L}\right\} \). קחו רגע לחשוב למה זה נכון.

טוב, אם יש לנו חיבור, צריך גם כפל, נכון? ההגדרה המתבקשת לכפל היא \( xy\triangleq\left\{ x^{L}y,xy^{L}|x^{R}y,xy^{R}\right\} \). ההגדרה הזו לא עובדת. למעשה, היא נכשלת בצורה מחפירה לחלוטין שבוודאי תשעשע אתכם אם תבינו בעצמכם למה. אז קחו רגע לחשוב ואל תקראו את השורה הבאה.

חשבתם? אוקיי. ההגדרה לא עובדת פשוט כי זו ההגדרה של חיבור. אותו דבר בדיוק. רק הסימבול שבו אני משתמש (או ליתר דיוק, לא משתמש, כי כפל מתואר כאן בלי סימבול) שונה.

אז צריך הגדרה אחרת. וההגדרה של קונווי היא לא פשוטה, אבל הוא מסביר אותה יפה בספר. אני רק אביא אותה כאן לצורך שלמות:

\( xy\triangleq\left\{ x^{L}y+xy^{L}-x^{L}y^{L},x^{R}y+xy^{R}-x^{R}y^{R}|x^{L}y+xy^{R}-x^{L}y^{R},x^{R}y+xy^{L}-x^{R}y^{L}\right\} \)

עכשיו יש לנו את כל ההגדרות הבסיסיות ואת האינטואיציה הראשונית, ואפשר להתחיל להתקדם אל היעד הנכסף הבא שלנו: המספר \( \frac{1}{3} \)! זאת, בפוסט הבא.