על משחקים ומספרים (חלק ב': מספרים. וקצת משחקים)

בפוסט הקודם התחלתי לבנות קבוצה של מספרים שהמוטיבציה אליהם הגיעה איכשהו מתוך משחקים קומבינטוריים. כזכור, הבניה הייתה פשוטה להפליא: כל מספר מיוצג על ידי אובייקט מהצורה \( \left\{ L|R\right\} \) כאשר \( L,R \) הן קבוצות, וכלל הבניה שלנו הוא ש”מספר” הוא אובייקט כזה כך ש-\( L,R \) הן שתיהן קבוצות של מספרים וכל איבר של \( L \) קטן ממש מכל איבר של \( R \), כאשר “קטן” מוגדר באמצעות היחס \( y\le x \) אם ורק אם לא קיים \( x^{R}\le y \) ולא קיים \( x\le y^{L} \).

ההגדרה הפשוטה להפליא הזו יוצרת קבוצה אדירה של מספרים. אבל לפני שנצלול לעומק העניין, בואו נחשוב לרגע על הגדרות דומות לה שאנחנו מכירים מהמתמטיקה ה”רגילה”. יש שתי הגדרות שקופצות מייד לראש - הגדרת הממשיים באמצעות חתכי דדקינד, והגדרת המספרים הסודרים בשיטה של ג’ון פון-נוימן.

המספרים של קונווי הם באופן כמעט מובהק הכללה של חתכי דדקינד (קונווי מתייחס לכך בעצמו, כמובן). כזכור, חתך דדקינד מתקבל מכך שאנחנו לוקחים את הרציונליים, \( \mathbb{Q} \), ומחלקים אותם לשתי קבוצות, \( L,R \), כך שכל איבר של \( L \) קטן מכל איבר של \( R \) (אפשר גם סתם לציין את \( L \) ולדרוש שהיא תהיה בעלת התכונה שאם \( x\in L \) ו-\( y\le x \) אז \( y\in L \)) ול-\( L \) אין איבר מקסימלי (תמיד אפשר להעביר את האיבר המקסימלי אל \( R \)). אינטואיטיבית הרעיון הוא שחתך כזה מגדיר את המספר הממשי שהוא הסופרמום של \( L \) (ואם הסופרמום הוא רציונלי, אז הוא יהיה האיבר המינימלי ב-\( R \)). המספר שחתך מגדיר הוא מה שתקוע בדיוק “בין” \( L,R \).

איך זה שונה ממה שקונווי עושה? ראשית, אצל דדקינד המספרים הרציונליים כבר קיימים; קונווי לא מניח קיום של שום דבר. שנית, אצל דדקינד \( L,R \) ביחד חייבות לכלול את כל הרציונליים ורק אותם, ואילו אצל קונווי הן יכולות להיות חלקיות ביותר, ויכולות גם לכלול מספרים לא רציונליים, כל עוד הם נבנו קודם. כך אצל קונווי אנחנו מקבלים ש-\( \left\{ -4|5,17\right\} \) הוא ייצוג שונה ל-0 (שהוגדר, כזכור, בתור \( \left\{ \ |\ \right\} \)) למרות שאין סיבה מיוחדת לומר שדווקא 0 הוא מה ש”תקוע” בין \( -4 \) ובין 5 ו-17. עדיין, אם איברי \( L \) ישאפו למספר כלשהו מלמטה, ואברי \( R \) ישאפו למספר כלשהו מלמעלה, אז \( \left\{ L|R\right\} \) הולך לייצג את המספר הזה, ואנחנו ננצל את זה בקרוב.

ומה פון-נוימן עושה? הוא מגדיר מספרים סודרים בתור קבוצת כל המספרים הקטנים מהם. כך 0 הוא \( \emptyset \), ואילו \( 1=\left\{ 0\right\} \), ו-\( 2=\left\{ 0,1\right\} \) וכן הלאה. בצורה הזו נבנים כל המספרים הטבעיים, ואז אפשר להמשיך עם זה הלאה: \( \omega=\left\{ 0,1,2,\dots\right\} \) ו-\( \omega+1=\left\{ 0,1,2,\dots,\omega\right\} \) וכך עד אינסוף ומעבר לו. הרעיונות הללו מתורגמים בצורה מיידית לגישה של קונווי, אם משאירים את \( L \) ריקה ומסתכלים על \( R \): \( 0=\left\{ \ |\ \right\} \) ו-\( 1=\left\{ \ |0\right\} \) ו-\( 2=\left\{ \ |0,1\right\} \) וכן הלאה; וגם פה אפשר להגדיר \( \omega=\left\{ \ |0,1,2,\dots\right\} \) ולהמשיך עם זה הלאה. אלא שאצל קונווי ה-\( \omega \) הזה חי באותו יקום כמו שאר המספרים, למשל \( \frac{1}{2} \), ולכן אפשר לחבר ולכפול אותם; ואפשר גם למצוא הופכי, כלומר קיים מספר שמתאים ל-\( \frac{1}{\omega} \) (והוא לא 0), כך שאנחנו מקבלים גם ייצוג פורמלי עבור אינפיניטסימלים; בקיצור, כיף חיים.

אבל לפני שנגיע לדברים הגרנדיוזיים הללו, אני צריך לפתור בעיה פשוטה - איפה \( \frac{1}{3} \)? טרם הצלחתי להגדיר אותו בכלל.

את מי כן הצלחתי להגדיר? את השלמים, וגם את \( \frac{1}{2}=\left\{ 0|1\right\} \) ואת \( \frac{1}{4}=\left\{ 0|\frac{1}{2}\right\} \) וכן הלאה עבור כל המספרים מהצורה \( \frac{1}{2^{n}} \). ומכיוון שיש לי גם חיבור, אז גם סכומים שלהם. זה טוב - זה ממש ממש טוב, מכיוון שלכל מספר ממשי קיים ייצוג בינארי, כלומר ייצוג בתור סכום של חזקות של 2 (כולל חזקות שליליות, כלומר \( \frac{1}{2^{n}} \)). בתור אימון, בואו נמצא את הייצוג הזה עבור \( \frac{1}{3} \).

איך בכלל מוצאים ייצוג בינארי עבור שבר? אולי יהיה לכם קל להיזכר קודם באופן שבו מבצעים חילוק ארוך בבסיס 10. אנחנו מחלקים את 1 ב-3: בתור התחלה, אנחנו בודקים כמה פעמים 3 נכנס ב-1 (0 פעמים) וכותבים את המספר 0, ואחריו את הנקודה העשרונית. עכשיו אנחנו לוקחים את השארית שלנו (שהיא 1, כי החילוק הניב מנה 0 ושארית 1). וכופלים אותה ב-10, כי 10 הוא בסיס הספירה שלנו. עכשיו אנחנו שוב מחלקים-עם-שארית את ה-10 הזה ב-3 ומקבלים מנה 3 ושארית 1. את המנה אנחנו כותבים בתור הספרה הבאה בייצוג, ואת 1 אנחנו שוב כופלים ב-10, וכן הלאה. כך מתקבל \( 0.333\dots \).

עבור בסיס 2 ההבדל היחיד הוא שאנחנו כופלים ב-2 במקום ב-10. לכן הספרה שלפני הנקודה העשרונית עדיין תהיה 0; אחריה נקבל עוד 0 (כי אחרי כפל ב-2 נקבל 2 שהוא קטן מ-3). אחרי כפל נוסף ב-2 נקבל 4, ולכן אחרי חלוקה ב-3 נקבל מנה 1 ושארית 1. שוב הגענו למחזוריות (שארית 1) ולכן קל כבר לראות שנקבל את הייצוג הבינארי \( 0.01010101\dots \). אם נכתוב את זה בתור טור, נקבל \( \frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\dots \) - כלומר, כל פעם כופלים את החזקה ב-4. זה טור הנדסי פשוט מאוד ואם אתם עוד לא משוכנעים שאני צודק, קל מאוד לחשב את סכומו:

\( \frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\dots=\frac{1}{4}\left(\sum_{n=0}^{\infty}\left(\frac{1}{4}\right)^{n}\right)=\frac{1}{4}\frac{1}{1-1/4}=\frac{1}{4}\frac{1}{3/4}=\frac{1}{3} \)

מסקנה: נגדיר את \( L \) שלנו להיות הקבוצה שכוללת את כל הסכומים החלקיים בפיתוח הזה: \( \frac{1}{4},\frac{1}{4}+\frac{1}{16},\dots \). אנחנו עדיין צריכים להגדיר את \( R \), כי לא לגמרי ברור לנו מה נקבל אם ניקח רק את \( L \) בזמן ש-\( R \) נותרת ריקה (התשובה, שאגיע אליה בהמשך, היא 1). בשביל \( R \) נראה לשאוף אל \( \frac{1}{3} \) “מלמעלה”. לצורך כך נתחיל עם \( \frac{1}{2} \) ונתחיל להחסיר. אם \( \frac{1}{2}-x=\frac{1}{3} \) אז

\( x=\frac{1}{2}-\frac{1}{3}=\frac{1}{6}=\frac{1}{2}\cdot\frac{1}{3}=\frac{1}{2}\left(\frac{1}{4}+\frac{1}{16}+\dots\right) \)

מסקנה:

\( \frac{1}{3}=\frac{1}{2}-\left(\frac{1}{8}-\frac{1}{32}-\dots\right) \)

ולכן קיבלנו את ההגדרה של \( \frac{1}{3} \) כמספר-סטיל-קונווי: \( \frac{1}{3}=\left\{ \frac{1}{4},\frac{1}{4}+\frac{1}{16},\frac{1}{4}+\frac{1}{16}+\frac{1}{64},\dots|\frac{1}{2},\frac{1}{2}-\frac{1}{8},\frac{1}{2}-\frac{1}{8}-\frac{1}{32},\dots\right\} \)

את \( \frac{1}{3} \) עשיתי בפירוט, אבל אני מקווה שאתם כבר משוכנעים שאפשר לקבל כך כל מספר רציונלי. אבל אם אפשר לקבל כל מספר רציונלי, אפשר לקבל כל מספר ממשי, כי הרציונליים צפופים בממשיים; ולכן באמצעות המספרים שהם חזקות של 2 שבנינו עד כה, אפשר לקבל את כל המספרים הממשיים.

קונווי מציג את הבניה כמתרחשת ב”ימים”. ביום הראשון בונים את 0; ביום השני את 1 ואת \( -1 \); ביום השלישי את \( 2 \) ו-\( -2 \) וגם את \( \frac{1}{2} \) ו-\( -\frac{1}{2} \) וכן הלאה. היום המעניין הבא בבניה הוא \( \omega \) (היום ה”אינסופי” הראשון) - ביום הזה מקבלים בבת אחת כל כל הממשיים שאינם חזקות של 2. אבל מקבלים בו יותר מזה - גם את \( \omega=\left\{ \ |0,1,2,\dots\right\} \) שתיארתי קודם.

ומה קורה אחר כך? ובכן, לכל מספר סודר יש יום בבניה שמתאים לו. ביום הזה ייבנה, באופן לא מפתיע, המספר הסודר הזה, אבל נבנים עוד דברים: למשל, מה זה \( \left\{ 0,1,2,\dots|\omega\right\} \)? זה מספר מוזר שאמור להיות גדול מכל הטבעיים אבל קטן מ-\( \omega \). זה משהו שלא קיים עבור סודרים; אנחנו קוראים בשם \( \omega \) לסודר הראשון שגדול מכל הטבעיים. אבל בבניה של קונווי המספר \( \left\{ 0,1,2,\dots|\omega\right\} \) הוא יצור חי וקיים, ואם חוקרים אותו קצת מגלים שהוא אמור להיות \( \omega-1 \) (כלומר, זה מספר שאם מחברים לו 1 מקבלים את \( \omega \)). ואז אפשר לבנות את \( \omega-2=\left\{ 0,1,2,\dots|\omega-1\right\} \), וכן הלאה את \( \omega-n \) לכל \( n \) טבעי.

אוקיי, זה קצת מוזר.

זה לא לגמרי מוזר - האובייקט שקונווי בונה אמור להיות שדה, ולכן פעולת החיסור חייבת להיות מוגדרת עבור כל שני איברים שלו. עדיין, זה לא אינטואיטיבי למי שהתרגל לסודרים במתכונת הסטנדרטית שלהם.

בואו נמשיך עם זה קצת ונראה לאן נגיע. מה יהיה המספר \( \left\{ 0,1,2,\dots|\omega,\omega-1,\omega-2,\dots\right\} =\left\{ n|\omega-n\right\} \)? מצד אחד הוא גדול מכל הטבעיים, מצד שני הוא קטן מכל ה-\( \omega-n \)-ים האפשריים. ובכן, מתברר שהוא \( \frac{\omega}{2} \) - אם נחבר אותו לעצמו נקבל \( \omega \). על פי ההגדרה הפורמלית של החיבור, אם נסמן לרגע את המספר הזה בתור \( x \), נקבל \( \left\{ x,x+1,x+2,\dots|\omega+x,\omega+\left(x-1\right),\omega+\left(x-2\right),\dots\right\} =\left\{ x+n|\omega+\left(x-n\right)\right\} \); אז איך אפשר לדעת שהיצור הזה שווה ל-\( \omega=\left\{ 0,1,2,\dots|\ \right\} \)?

ובכן, זכרו את האופן שבו הוגדר שוויון - צריך להוכיח אי-שוויון דו כיווני. כלומר, להוכיח ש-\( 2x\le\omega \) וגם \( \omega\le2x \). כדי שהדבר הראשון יתקיים אנחנו צריכים לוודא שאין “דוגמה נגדית” לאי השוויון - כלומר, שלא מתקיים \( \omega\le2x^{L} \) ולא מתקיים \( \omega^{R}\le2x \) (קחו רגע ונסו להזכיר לעצמכם למה דווקא שני אי השוויונים הללו). אי השוויון \( \omega\le2x^{L} \) הוא קל, כי כל איבר מהצורה \( 2x^{L} \) הוא מהצורה \( x+n \) כאשר \( n \) טבעי, אבל אנחנו יודעים ש-\( x<\omega-n \) (מהגדרתו) ולכן נקבל ש-\( x+n<\omega \) (כמובן, אתם צריכים להאמין לכך שכללי האריתמטיקה מתקיימים, אבל לא לדאוג - קונווי מוכיח את זה). כעת, \( \omega^{R}\le2x \) עוד יותר קל כי אין בכלל איברים מהצורה \( \omega^{R} \). זה מוכיח ש-\( 2x\le\omega \).

בשביל הכיוון השני צריך להוכיח שלא מתקיים \( 2x\le\omega^{L} \) ושלא מתקיים \( 2x^{R}\le\omega \). הראשון ברור - כל \( \omega^{L} \) הוא מספר טבעי \( n \), ואנו יודעים ש-\( x+n<2x \). עבור השני, זה נובע מכך שכל \( 2x^{R} \) הוא מהצורה \( \omega+\left(x-n\right) \) כאשר אנו יודעים ש-\( n<x \) לכל \( n \) טבעי, ולכן (שוב, עם אמונה בכללי אריתמטיקה כלשהם) מקבלים את המסקנה.

כרגיל, הוידוא הזה היה קצת מציק. האם אין דרך יותר טבעית להסתכל על הגדרה כלשהי של מספר ולראות בקלות שהוא זהה למספר קיים? ובכן, יש, והגיע הזמן שנראה אותה. קונווי מכנה את הכלל הזה “כלל הפשטות”, לא בגלל שהוא פשוט (הניסוח קצת מבלבל) אלא בגלל שהוא אומר שבהינתן מספר כללי \( \left\{ L|R\right\} \) ואנו רוצים לדעת לאיזה מהמספרים שקונווי בנה הוא שוה, אז המספר הנכון יהיה המספר הכי פשוט שמתאים, כאשר “פשטות” כאן נקבעת על פי ה”יום” שבו המספר נבנה אצל קונווי. אמרתי שזה מבלבל, נכון? אבל 0 פשוט יותר מ-1, ו-1 פשוט יותר מ-2 וכדומה. וכל המספרים הממשיים שנבנו ביום ה-\( \omega \) הם פשוטים באותה מידה, אבל מסובכים יותר מכל אלו שבאו לפניהם. הרעיון הוא שמספר “מסובך יותר” נבנה מתוך מספרים פשוטים יותר - הם יהיו האופציות שמופיעות באגף ימין ושמאל שלו.

הנה הניסוח המדויק של המשפט: אם \( x=\left\{ x^{L}|x^{R}\right\} \) ו-\( z \) הוא מספר כלשהו כך ש-\( x^{L}<z \) וגם \( z<x^{R} \) לכל \( x^{L},x^{R} \), אבל התכונה הזו לא מתקיימת על ידי אף אופציה של \( z \) (כלומר, לא על ידי אף \( z^{L} \) או \( z^{R} \)), אז \( x=z \).

ההוכחה די קלה, ודי דומה למה שעשינו לפני רגע. נוכיח ש-\( z\le x \). האפשרויות שצריך לשלול הן ש-\( x^{R}\le z \) (נשלל, כי ההנחה היא ש-\( z<x^{R} \)) וש-\( x\le z^{L} \). כדי לשלול את האפשרות הזו נרצה להראות שנובע ממנה ש-\( z^{L} \) מקיים את אותה תכונה כמו \( z \) המקורי, כלומר ש-\( x^{L}<z^{L} \) וגם \( z^{L}<x^{R} \). הראשון מבין שני אלו נובע מיד, כי \( x^{L}<x \); עבור השני, נשתמש בכך ש-\( z^{L}<z<x^{R} \).

נשאר להוכיח ש-\( x\le z \). כאן האפשרויות שצריך לשלול הן ש-\( z\le x^{L} \) (נשלל מייד כי \( x^{L}<z \)) וש-\( z^{R}\le x \); את זה שוללים באופן סימטרי לקודם. זה מסיים את המשפט.

עכשיו ברור מייד מיהו \( \left\{ x+n|\omega+\left(x-n\right)\right\} \): מצד אחד, \( \omega \) מתאים, כי הוא קטן מכל מי שבאגף ימין וגדול מכל מי שבאגף שמאל; מצד שני, כל האופציות של \( \omega \) הן טבעיים, וכולם קטנים ממישהו מאגף שמאל, כך שזה מסיים את הסיפור. עכשיו, באופן דומה, אפשר להסתכל על \( \left\{ n|\frac{\omega}{2}-n\right\} \) ולקבל שהוא שווה ל-\( \frac{\omega}{4} \), כי אם נסמן אותו ב-\( x \) ונחבר אותו עם עצמו, נקבל את \( \left\{ x+n|\frac{\omega}{2}+\left(x-n\right)\right\} \), וכאן בבירור \( \frac{\omega}{2} \) מתאים אבל אף מספר טבעי לא, וגם אף מספר מהצורה \( \omega-n \) לא, כי \( x<\frac{\omega}{2} \) ולכן נקבל ש-\( \frac{\omega}{2}+\left(x-n\right)<\frac{\omega}{2}+\frac{\omega}{2}-n=\omega-n \).

אז אנחנו יודעים להגדיר את \( \frac{\omega}{4} \), ובדרך דומה נקבל את \( \frac{\omega}{2^{n}} \) לכל \( n \) טבעי. וכבר ברור לנו איך מכאן מקבלים את \( \frac{\omega}{3} \) וכדומה.

עכשיו זה זמן טוב לעצור ולפרמל עוד יותר את ההגדרות, להוכיח שהחיבור והכפל אכן מתנהגים כמו שצריך, שאנחנו מקבלים שדה, וכדומה. אבל זו לא עבודה טריוויאלית וקונווי עושה אותה מצויין ב-On Numbers and Games, כך שאני ממליץ למי שהצלחתי לסקרן אותו לנסות ולקרוא את הספר. גם את הדיון המתבקש בשאלה האם הבניה של קונווי “טובה” יותר מהבניות הקיימות אני משאיר לספר - קונווי מדבר על יתרונות וחסרונות (ולא חורץ דין לשום כיוון, לתשומת לב הטרחנים המתמטיים). דבר אחד שקונווי מציין בתור יתרון ולדעתי הוא דווקא חסרון הוא האופן שבו נדרשת רק הגדרה אחת כדי לקבל את כל המספרים בבת אחת. מצד אחד, אין ספק שזה מגניב בצורה פסיכית; מצד שני, זה לא האופן שבו אני חושב על מספרים, ואני בהחלט חושב שיש יתרון בביצוע הפרדות חדות יחסית בין הטבעיים, השלמים, הרציונליים והממשיים, ובבניה של כל אחד מהם מתוך הקודמים על ידי טכניקות שונות. בשורה התחתונה לא הייתי הופך את המספרים של קונווי למשהו שאני מציג למי שרואה את בניית המספרים בפעם הראשונה, אבל זה בהחלט משהו שכדאי מאוד לראות מתישהו, ולא בשלב מתקדם מדי.

בואו נחזור קצת למשחקים, לסיום. ראשית, הנה שאלה מתבקשת: האם \( \omega \) וחבריו צצים מאליו גם בניתוח משחקים? התשובה חיובית, אבל המשחק צריך להיות אינסופי במובן כלשהו - לכל הפחות, צריך שיהיו אינסוף מהלכים התחלתיים אפשריים במשחק עבור אחד השחקנים (אפילו את \( \frac{1}{3} \) אי אפשר לקבל במשחק שבו יש רק מספר סופי של מהלכים). את \( \omega \) ספציפית אפשר לקבל על ידי לוח פשוט מאוד של הקנבוש - כזה שיש בו מגדל אינסופי של קווים שכולם בצבע של אליס. המהלך היחיד של אליס יסלק את כל המגדל חוץ מאשר מספר סופי של קווים שלו, כלומר יעביר אותנו לאחד מהמספרים הטבעיים, ולכן ברור שקיבלנו את \( \omega \).

עכשיו אני רוצה לדבר על משחקים קומבינטוריים שיש בהם מצבים שלא ניתנים לתיאור על ידי מספרים - כלומר, שנראה איך \( \left\{ L|R\right\} \) משמש גם בתור סימון של משחק. כבר אמרנו בפוסט הקודם ש-\( L \) היא קבוצת המהלכים של אליס ו-\( R \) הוא קבוצת המהלכים של בוב, כאשר כאן מהלך מזוהה עם המשחק החדש שהוא מייצר מתוך המשחק הקיים (כאן “משחק” מתבטא גם במצב הנוכחי של ה”לוח”). בשביל שליצור הזה נקרא מספר היה חייב להתקיים שכל איבר של \( L \) קטן מכל איבר של \( R \), אבל במשחק כמו \( \left\{ 1|-1\right\} \) זה לא קורה. המשמעות של המשחק הזה פשוטה - אם אליס מתחילה, היא יכולה לנצח תמיד, בלי תלות בבוב; ואם בוב מתחיל, הוא יכול לנצח תמיד, בלי תלות באליס (“לכפות נצחון”). זה בבירור לא מתאים למספרים שראינו עד כה: 0 תיאר משחק שבו מי שמתחיל, מפסיד, ואילו כל מספר אחר תיאר משחק שבו אחד משני השחקנים יכול לכפות נצחון (אם המספר חיובי, אליס יכולה לכפות נצחון, ואם הוא שלילי אז בוב יכול).

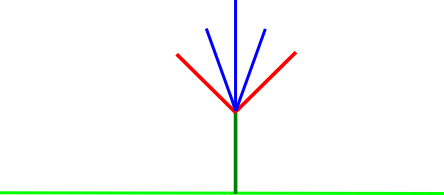
קונווי מסמן את זה כך: אם \( G \) הוא משחק, אז \( G>0 \) אם אליס יכולה לכפות נצחון; \( G<0 \) אם בוב יכול לכפות נצחון; \( G=0 \) אם השחקן השני (לא זה שמתחיל) יכול לכפות נצחון; ו-\( G||0 \) אם השחקן הראשון יכול לכפות נצחון: לסיטואציה כזו הוא קורא Fuzzy. הדרך הכי טובה להבין את ההתנהגות המוזרה שלה היא באמצעות משחק לדוגמה. במקרה הזה, וריאציה על הקנבוש. כזכור, בהקנבוש לאליס מותר למחוק רק קשתות אדומות, ולבוב מותר למחוק רק קשתות כחולות; בואו נהפוך את זה למעניין יותר על ידי הוספת קשתות שגם לאליס וגם לבוב מותר למחוק - ירוקות.

הנה משחק לדוגמה:

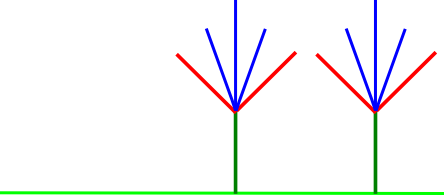
כאן בבירור מי שמתחיל יכול לכפות נצחון, על ידי לקיחת ה”גבעול” הירוק, מה שהופך את המשחק הזה למטופש למדי. אבל כרגיל בעניינים כאלו, וריאציה קטנה הופכת אותו למעניין - מה אם היו לנו שני “פרחים”?

עכשיו לקחת את הגבעול של אחד הפרחים זה מתכון בטוח להפסד, כי השחקן השני יקח את הגבעול של הפרח השני. לכן הקרב יתחולל בכלל ב”עלים” של הפרחים, והמפסיד יהיה מי שנשאר בלי עלים בכלל לקחת וחייב לקחת את אחד מהגבעולים. כלומר, קיבלנו את אותו משחק כמו המשחק הבא:

והמשחק הזה הוא \( -2 \). אז אם נסמן ב-\( G \) את המשחק המקורי, קיבלנו ש-\( G+G=-2 \), אבל אי אפשר להסיק מכך ש-\( G=-1 \); אנחנו רואים שבהכרח משחקים שהם Fuzzy לא יתנהגו נחמד כמו מספרים. יותר מכך - אם נשנה את התצורה של העלים של \( G \) על ידי כך שנחליף בין הצבעים שלהם נקבל ש-\( G+G=2 \), וזאת למרות ש-\( G \) עצמו לא השתנה ונותר משחק שבו המתחיל יכול לנצח בצעד הראשון שלו. זו הסיבה שקונווי משתמש בתיאור Fuzzy למשחקים כאלו - אנחנו יודעים שהם נמצאים בתוך מין “ענן” כזה סביב ציר המספרים, אבל המיקום המדויק שלהם תלוי בפרטים נוספים.

כמובן, בניתוח של רוב המשחקים סביר שיצוצו מצבים שהם Fuzzy, אחרת אלו משחקים די מוזרים - כאלו שהם מוטים מראש לטובת אחד מהשחקנים, ולא משנה אם הוא מתחיל או שני (או, עבור 0, משחקים שבהם מי שמתחיל מפסיד). בהקנבוש הרגיל זה לא קורה, כי המשחק מוטה: יש קשתות שהן רק של אליס וקשתות שהן רק של בוב, בלי קשר לשאלה מי משחק מתי. אם כן, אולי כדאי שנסתכל על משחק שאיננו מוטה בצורה הזו? למשל, נים, שכבר הזכרתי בפוסט הקודם אבל נמנעתי מלדבר עליו עד כה כי בניתוח שלו לא צצים המספרים הסוריאליסטיים כפי שהם צצים עם הקנבוש. כמובן, הדיכוטומיה נים-או-הקנבוש היא קצת שקרית; הקנבוש המוכלל, עם הקשתות הירוקות, כולל את נים בתור מקרה פרטי: משחק הקנבוש הוא בעצם נים אם כל הקשתות שלו ירוקות והוא מורכב ממספר מסלולים זרים (אין “התפצלות”).

למי מכם שלא מכירים את נים או זוכרים אותו, יש לי פוסט על הנושא שגם נותן ניתוח יפה של האסטרטגיות במשחק. הפעם אני רוצה להתמקד באספקט ה”מספרי” של המשחק. בואו נמשיך לנקוט בגישה של קונווי, ונסמן ב-\( *n \) את המשחק שמתאים לנים בעל ערימה אחת עם \( n \) גפרורים (קונווי קורא להם Nimbers, אבל בעברית זה כבר לא עובד - “מספנים”?). פורמלית, \( *0=\left\{ \ |\ \right\} \) ו-\( *1=\left\{ *0\ |*0\right\} \) ובאופן כללי \( *n=\left\{ *0,*1,\dots*\left(n-1\right)|*0,*1,\dots*\left(n-1\right)\right\} \).

ה”מספרים” הללו מתנהגים בצורה מוזרה, כמובן. בתור התחלה, קל לראות שמתקיים \( *n+*n=*0 \) (חיבור, כזכור, הוא מה שמקבלים אם לוקחים את שני המשחקים ושמים אותם זה ליד זה, כך שכל אחד בתורו יכול לבחור באיזה משחק לשחק). כלומר, מי שמתחיל לשחק על משחק מהצורה \( *n+*n \) מפסיד, כי הצד השני יכול לבצע “תמונת ראי” לכל מה שהוא עושה על המשחק המקביל (דהיינו, בכל רגע נתון במשחק, אחרי שהשחקן הראשון ביצע מהלך השני יכול לעשות מהלך שבסופו עדיין יהיו שתי ערימות מאותו גודל). לעומת זאת, אם \( n\ne k \) אז \( *n+*k \) הוא משחק שבו השחקן הראשון מנצח תמיד (מהלך הפתיחה המבריק הוא לאזן את גדלי שתי הערימות), כלומר \( *n+*k \) הוא משחק Fuzzy ואינו ניתן לתיאור בידי מספר רגיל. אבל מה המספרנים שמתאים לו? ובכן, אין לי כרגע סט כללים נחמד, אבל בואו נלך בעקבות קונווי ונראה כמה דוגמאות.

בתור התחלה, מהו \( *1+*2 \)? אנחנו רוצים למצוא ערימה שלישית שאם נשים ליד שני אלו, נקבל משחק שערכו 0. ברור שלהוסיף ערימה מגודל 1 או 2 לא יעבוד, כי המתחיל יסלק את הערימה מהגודל יוצא הדופן ונישאר עם שתי ערימות מאוזנות (משחק שבו המתחיל מפסיד, ומכאן שהמתחיל במשחק המקורי ניצח). לעומת זאת ערימה מגודל 3 תעבוד - לא משנה מה מהלך הפתיחה של השחקן הראשון, השחקן השני יוכל להביא אותנו למצב של שתי ערימות מאוזנות. 4 כבר לא מתאים כי לשחקן הראשון יש מהלך פתיחה של צמצום ערימת ה-4 לערימת 3; באופן דומה גם כל גודל הגדול מ-4 לא יעבוד. מכאן שערימה בגודל 3 היא המועמד המתאים היחיד כאן, וקיבלנו ש-\( *1+*2=*3 \).

כמובן, כבר אנחנו רואים שקורה כאן משהו מוזר. השוויון שלעיל נובע מכך ש-\( *1+*2+*3=0 \), ומכך ש-\( *3=-*3 \); אבל באותה המידה היינו יכולים לכתוב גם \( *2+*3=*1 \). אז תשכחו מחוקי החשבון הרגילים.

בואו ננסה עוד דוגמה שיש אצל קונווי: \( *1+*4+*5 \). גם כאן הטענה היא שמי שמתחיל, מפסיד. למה? סילוק ערימת ה-1 בוודאי מוביל להפסיד. הקטנה של ערימת ה-4 ל-2 או 3 תאפשר לשחקן השני להעיף את ערימת ה-5 ולהעביר את המשחק ל-1,2,3 שכבר ראינו שהמתחיל מפסיד בו, והקטנה של ערימת ה-4 ל-1 תיצור שתי ערימות זהות. אותו דבר קורה עם 5 - הקטנה שלה ל-4 תיצור שתי ערימות זהות, והקטנה רצינית יותר תיצור את \( 1,2,3 \). קיבלנו ש-\( *1+*4=*5 \).

כאן זו נקודה טובה לעצור - בינתיים. מן הסתם אני רק מגרד את קצה הקרחון של התחום הזה, אבל בעיה עיקרית היא שקשה לי להתחרות עם קונווי; שני הספרים שאני מסתמך עליהם הם מופת של כתיבה, ואני ממליץ לכם לקרוא אותם אם התעניינתם במה שהוצג עד כה. כאמור, On Numbers and Games הוא המתמטי-פורמלי יותר, בזמן ש-Winning Ways הוא יותר קליל באופיו, אבל שניהם מאוד מומלצים.