אז בנוגע למתמטיקה ובית הספר...

עד היום נמנעתי כמעט לגמרי מהתייחסויות בבלוג אל מה שהוא אולי הדבר החשוב ביותר למרבית הציבור בכל הנוגע למתמטיקה - האופן שבו נלמדת מתמטיקה בבתי הספר. האדם הממוצע הולך לפגוש את המתמטיקה כמעט אך ורק במסגרת הזו, והמסגרת היא זו שתקבע מה תהיה ההתרשמות שלו מהמתמטיקה. וכפי שכולנו יודעים, ההתרשמות הזו היא כמעט תמיד שלילית. וכולנו תוהים - האם לא ניתן לעשות את זה אחרת? בשנים האחרונות השאלה הזו עולה שוב ושוב בדיונים על האם כן צריך ללמד מתמטיקה לבגרות, או לא ללמד, והאם 5 יחידות, או לא 5 יחידות, והאם עתיד ההייטק של המדינה בסכנה, או לא בסכנה, ועוד כהנה וכהנה.

אז למה לא דיברתי על זה עד היום, בעצם? התשובה פשוטה: כי אני לא יודע כלום על חינוך מתמטי ברמת בית הספר.

יש לי נסיון כלשהו בהוראה של סטודנטים, ועוד נסיון קטן עם תלמידים מצטיינים בגיל חטיבת ביניים. האתגר שתלמידים כאלו מציבים בפני המורה הוא נמוך יחסית. אלו תלמידים שרוצים לדעת את החומר (סטודנטים אולי לא אוהבים את החומר בהכרח, אבל הם רוצים לדעת אותו כדי להצליח בקורס, והם על פי רוב לא נמצאים בלימודים האקדמיים כי מכריחים אותם) ושומרים על קשב גבוה ולא מפריעים כמעט בכלל. לעומת זאת, האתגר שהמורה עומד בפניו בכיתה ממוצעת של תלמידים הוא אדיר. מאמץ גדול נדרש רק כדי לשמור על הקשב ולמנוע הפרעות, רמת התלמידים לא אחידה, והמורה עצמו לאו דווקא שולט בצורה מיטבית בחומר. וזה מבלי שהתחלנו לדבר בכלל על חומר הלימוד. נסיון לחשוב איך צריכה להיראות, בעצם, תוכנית לימודים שגם יהיה לה סיכוי להיות מועברת בפועל בכיתות אמיתיות עם מורים אמיתיים זה אתגר כביר, ומה שנראה לנו נחמד על הנייר, כלל לא מובטח שיעבוד בפועל. הדבר היחיד שאני יכול לומר בודאות הוא שאין לי מושג וחצי מושג בנושא וכל מה שאני אומר צריך להילקח בערבון מוגבל גדול מאוד בשל כך.

עדיין, אולי כדאי שאגיד את דעתי, ושהדעה הזו לא תובא בתור סוף פסוק אלא בתור ההזמנה שלי להתחיל דיון, שממנו אני בוודאי אחכים (וכמובן, מאוד אשמח אם אנשים שאכן משתתפים בקביעת מדיניות לימודי המתמטיקה בבתי הספר ישתתפו בו).

הטרגדיה של שימוש בטובה בתור מפוח עלים

כמעט בכל דיון על מתמטיקה בבית הספר שאני משתתף בו צץ מתישהו מאמר בשם A Mathematicians Lament של פול לוקהארט שעוסק בחינוך מתמטי בבתי הספר. אני ממליץ על המאמר הזה (אבל לא מסכים עם כולו), אבל לא אגיד עליו כמעט כלום כאן אלא אנסה לכתוב פוסט שיעמוד בפני עצמו. מה שאני רוצה לשאול ממנו הוא את הפתיחה שלו, שמנסה להבהיר עד כמה המתמטיקה שנלמדת בבתי הספר נדמית לנו, האנשים ש”מכירים” מתמטיקה, בתור פספוס. אם תרצו, זהו נסיון להסביר מדוע הרצון שלנו לגרום לאנשים לאהוב מתמטיקה נידון לכשלון עוד לפני שניסינו בכלל - אנחנו מלמדים את הדבר הלא נכון. אבל כמובן, זה לא אומר שאנחנו מלמדים בטעות סינית במקום מתמטיקה; זה האופן שבו מלמדים חומר שללא ספק שייך למתמטיקה שכל כך בעייתי.

האנלוגיה של לוקהארט היא ללימודי מוזיקה. הוא מתאר מוזיקאי מבועת שמתעורר מחלום שבו לימודי המוזיקה עוסקים בקריאת דפי תווים. ביכולת להעתיק דפי תווים, לזהות סולמות, קונטרפונקטים ועוד כהנה וכהנה. מה שהם לא עושים בשום צורה הוא לשמוע מוזיקה או אפילו לראות כלי נגינה. אתם מוזמנים לקרוא את התיאור המלא - המאמר נפתח בו - עבורי התיאור הזה מצמרר לגמרי, כי הוא קולע בול אל לימודי מתמטיקה בבתי הספר כפי שאני מכיר אותם.

לוקהארט הולך לכיוון המוזיקה כי הוא רוצה לתאר את המתמטיקה בתור אמנות, בדומה לכך שהמוזיקה היא אמנות, אבל אני לא רוצה ללכת לכיוון הדיון הזה ורוצה לתת אנלוגיה אחרת. כמעט כל דיון על חינוך מתמטי בבית הספר מדבר על השימושיות של המתמטיקה, ועל כמה שהיא קריטית כדי לקיים לימודי מדע וטכנולוגיה גבוהים, ובשביל שתעשיית ההייטק תתקיים, וכדי שהשמש תזרח מחר ועוד כהנה וכהנה. עוד ביטוי אהוב בהקשר הזה הוא התיאור של המתמטיקה כארגז כלים. אז יאללה, בואו נלך אל הגישה הזו עבור מקצוע לימודים בדיוני - לימודי איקאה.

אני מניח שלא מעטים הקוראים שמתעבים את איקאה בכל ליבם או לא מבינים מה לכל הרוחות הקטע. וזה בסדר - הרי אותו הדבר קורה גם עם מתמטיקה. אבל בואו תחשבו לרגע על חובב איקאה מושבע. אחד כזה שאוהב את הרהיטים ואוהב להשתמש בהם ואוהב להרכיב אותם. אחד שבשבילו זה כמו משחק לגו גדול, עם ערך מוסף אחר כך של רהיט שאפשר לשים בו בגדים, או לישון בו, או לשבת לאכול עליו. והוא אוהב לבקר בחנות של איקאה (בשעות שבהן אין בני אדם - הוא יודע בדיוק מה הן כי הוא חובב איקאה), להסתכל על המגוון האדיר של רהיטים, אולי אפילו לשוטט קצת בדירות לדוגמא של “בואו תראו איך אנחנו וכל משפחתנו המורחבת והחתול וחזירון המחמד גרים בכיף ב-13 מטר מרובע!!!!!”. והוא אוהב את תהליך הבניה - לפתוח את הקרטון, לשים לעצמו מוזיקה קלאסית ברקע, להצמיד לוח אל לוח, לסובב ברגים, לדפוק בפטיש, והופס - לראות איך מערימה אקראית של דברים צץ לו רהיט חדש. ואולי הוא אפילו אוהב לעשות האקינג - לקחת את חלקי הרהיטים ולבנות אותם שלא על פי ההוראות, כדי לקבל משהו חדש שמתאים לו אישית. והוא כנראה גם מפרסם את מעלליו באינטרנט לחבריו חובבי האיקאה, ואולי גם יומנים מצולמים, וכדומה.

ועכשיו האיש הזה מגלה שבבתי הספר התחילו ללמד “לימודי איקאה”. והוא קופץ לראות איך השיעורים מתנהלים, ורואה שהם מתנהלים ככה: בשיעור הראשון מציגים תמונה מאמצע מדריך בניה של מיטה. אנחנו בדיוק בשלב שבו לוקחים את בורג מס’ 11467 ומבריגים אותו לתוך לוח. עם מברג שטוח. המורה מסביר את זה לתלמידים כמה פעמים, באופן זה: ב-ו-ר-ג מספר אחד-אחד-ארבע-שש-שבע. את הבורג מבריגים אל תוך החור האמצעי בקצוות של הלוח. האמצעי. בורג מס’ 11467. להבריג. עם מברג. שטוח. בחור האמצעי. בקצוות. של הלוח. עכשיו בואו ונעשה את זה!

במשך יתר השיעור התלמידים מבריגים את הבורג לתוך הלוח. ושוב. ושוב. ושוב. היד מתחילה לכאוב די מהר, אבל הגאווה גדולה - אנחנו כעת שולטים בבורג! אנחנו יודעים להבריג את הבורג לתוך הלוח! את בורג מספר אחד-אחד-ארבע-שש-שבע!

חובב האיקאה חוזר לשיעור הבא. בשיעור הבא שכחנו כבר מהמיטה, ועכשיו אנחנו מתעסקים עם שולחן, או משהו. כמקודם, אנחנו רואים רק תמונה מאמצע המדריך. בתמונה הזו דוחפים איזה משהו מעץ לתוך חורים באיזה… משהו. והמורה אומר: יש להקפיד לדחוף את משהו מעץ מספר אחד-אפס-אחד-שלוש-חמש-אפס! לא את אחד-אפס-אחד-שלוש-חמש-שש! האחד ארוך יותר מהשני! השוו אורכים! בדקו! דחפו את המשהו מעץ! עם האצבעות! מי שקשה לו עם האצבעות, שיאחז פטיש! וכעת, הבה ונתרגל!

ובמשך יתר השיעור התלמידים דוחפים משהו מעץ לתוך משהו אחר מעץ. חלה התרגשות זוטא כשאחד התלמידים דוחף בטעות פנימה משהו מעץ מספר 101356 והוא נתקע שם. המורה המבוהל רץ להביא פלייר ושולף את המשהו השגוי מעץ; התלמידים מתלהבים לרגע מהפלייר אבל המורה מזהיר אותם שזה לא קשור לחומר הלימוד ושזה מתקדם מדי בשבילם אז שישכחו מזה.

וזהו.

ככה מתנהלים כל “לימודי איקאה”. בכל משך בית הספר.

חובב האיקאה מבועת. כלומר, הוא מסכים לגמרי שמה שלומדים בשיעורים הללו רלוונטי לאיקאה; אלו דברים שהוא עצמו, בתור חובב איקאה, עושה כל הזמן. זה כישור שהוא הכרחי לבניית רהיטים מאיקאה. אבל בשם האלים הסקנדינביים, למה מלמדים את זה ככה?!

הסיפור נשמע קיצוני, כמובן, אבל לפחות אני מרגיש שזה המצב בפועל בכל הנוגע למתמטיקה תיכונית. לא כולה; אבל חלקים נרחבים יותר מדי ממנה. ואני מאמין שיש לזה השלכה ישירה על תופעת “שנאת המתמטיקה” הידועה לשמצה.

עכשיו צריך לעצור ולשאול את עצמנו כמה שאלות. ראשית, האם התיאור שלי נכון? האם אני צודק? ואולי זה היה נכון כשאני למדתי בבית הספר אבל זה לא נכון עכשיו? ואולי זה נכון עכשיו אבל אוטוטו תהיה תוכנית לימודים חדשה לבתי הספר שתטפל בזה? אלו שאלות טובות. אנסה בהמשך לתת דוגמה או שתיים למשהו שקורה עכשיו בחומר הלימוד, אבל לדבר על מה שיקרה אולי בעתיד אני לא יכול.

שנית, וזו השאלה הקשה יותר, האם אופן הלימוד הזה הכרחי? האם נסיון ללמד מתמטיקה בדרך שלי נראית יפה או מעניינת יותר נידון לכישלון? על זה אני לא יכול לענות, כי אין לי נסיון בהוראה. אני כן יכול להגיד מה לדעתי כדאי לנסות, או מה הכיוון שנראה לי שצריך ללכת אליו, על מנת להפוך את המתמטיקה התיכונית למעניינת יותר, וזה מה שאנסה לעשות.

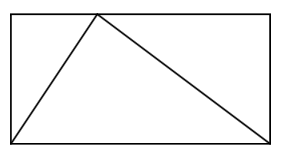
אני כן רוצה להביא דוגמה אחת מהמאמר של לוקהארט שהיא פשוט נפלאה, לגבי מהי מתמטיקה יפה, מהי מתמטיקה טכנית, וכמה דק ההבדל ביניהן לפעמים. לוקהארט מביא, לכאורה משום מקום, חידה: הנה ציור של משולש בתוך מלבן, ואנחנו רוצים לדעת איזה אחוז משטח המלבן תופס המשולש (יש שלושה משולשים, אני מתכוון לזה הגדול, שהצלע התחתונה שלו היא הצלע התחתונה של המלבן):

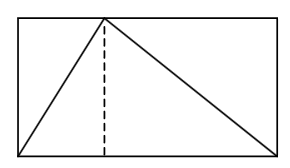
החידה הזו מעלה אוטומטית תחושות רעות: למי אכפת בכלל כמה שטח תופס המשולש? מה זה חשוב? איפה משתמשים בזה בחיים האמיתיים? איכס זה טכני, צריך לחשב שטחים, ואחוזים! מאיפה לנו לדעת, צריך למצוא כלי מדידה! ועוד ועוד ועוד. הבנתם את הקטע. גם בי החידה הזו מעלה את התחושות הללו. אבל צריך להבין שגם אצל המתמטיקאים יש את התחושות הללו, וחלק ממה שהמתמטיקאים עושים הוא למצוא דרך לעקוף אותן. ומה המתמטיקאים עושים כאן? פשוט מאוד - מציירים קו אנכי מהקודקוד העליון של המשולש אל הצלע התחתונה של המלבן:

והשינוי הקטן הזה פותר הכל. כי פתאום אנחנו רואים שחילקנו את המלבן לארבעה משולשים, כשכל זוג משולשים (שני הימניים ושני השמאליים) הם זהים. אם הם זהים, ברור שהמשולש תופס בדיוק חצי משטח המלבן, וזה מסיים את הכל. זו לא הוכחה מתמטית פורמלית, כי עדיין צריך להראות שבאמת כל זוג משולשים הם זהים, אבל זה עניין של חפיפת משולשים שהוא פשוט למדי, וזה לא העיקר כאן, אלא האופן שבו בעיה מסובכת וגועלית הפכה פתאום לטריוויאלית. אבל למה זה מעניין? ובכן, כי כמעט בלי לשים לב הוכחנו פה את הנוסחה של שטח משולש - שטח המשולש הוא חצי משטח המלבן, ושטח המלבן הוא מכפלה של אורך צלעותיו, אז אפשר לקחת את הצלע התחתונה (שהיא גם צלע של המשולש) ולכפול אותה בצלע השניה (שהיא גם האורך של האנך שהורדנו) ולחלק ב-2. קיבלנו את הנוסחה \( S=\frac{bh}{2} \) לשטח משולש שלרוב פשוט מפילים על התלמידים משום מקום ואז נותנים להם לפתור תרגילים איתה. למה, למה להפיל אותה משום מקום כשכל כך פשוט ויפה להראות איך מגיעים אליה? ההגעה אליה היא יותר מתמטיקה מאשר מאות תרגילים טכניים שבהם התלמידים “ישתמשו” בנוסחה הזו.

ועכשיו שימו לב שבהוכחה הזו השתמשנו בכל מני דברים - בכך שאנחנו בכלל מכירים מלבנים ומשולשים, ובכך שאנחנו יודעים שבמלבן הזוויות הן 90 מעלות, ובכך שאנחנו יודעים מה זה אנך, ואת הקטע הזה של לחלק ב-2, ועוד ועוד. אנחנו צריכים ידע ושליטה טכנית כלשהם כדי להבין מה הולך בהוכחה. אבל זו דוגמה ליישום יפה של הידע הזה. בבתי הספר זה לא ממש מה שקורה.

האם זו דוגמת מחץ שתשכנע אנשים שמתמטיקה היא יפה? כמובן שלא. אני מניח שרוב האנשים יסתכלו על הדוגמה הזו ועדיין יגידו “מה זה גועל הנפש הזה ואיך אתה אומר שהוא יפה?”. אבל אני מאמין שיהיו גם אנשים שיגידו “שמע, עד עכשיו לא הבנתי על מה אתה מדבר, אבל עכשיו זה אולי טיפה יותר ברור”. וניסיתי למלא את הבלוג בעוד אינספור דוגמאות אחרות, שאולי אחריהן זה יהיה עוד יותר ברור.

מדוע כן ללמד מתמטיקה?

בואו ננסה להבין על מה בעצם לומדים בבתי הספר. כיתות בית הספר בישראל מתחלקות לשלוש “רמות” שונות - בית ספר יסודי (כיתות א’ עד ו’), חטיבת הביניים (ז’ עד ט’) והתיכון (י’ עד י”ב). אני אפרט עכשיו מה לומדים בכל כיתה, אבל למי שאין לו כוח הנה התקציר: אני חושב שמה שלומדים עד וכולל חטיבת הביניים הוא בעיקרון טוב, חשוב והכרחי. משהו שכדאי שכל אדם ידע, ואפילו חלקו יהיה שימושי. עוד יותר בקצרה: בבית הספר היסודי לומדים אריתמטיקה (פעולות חשבון בסיסיות) וטיפה גאומטריה; בחטיבת הביניים לומדים יותר גאומטריה ואלגברה בסיסית (פתרון משוואות, חזקות, שורשים וכדומה). ובתיכון מתחילים להתפרש על שלל נושאים שבסופו של דבר נבחנים עליהם בבגרות. ב-3 יחידות לימוד הנושאים כוללים גאומטריה אנליטית, טריגונומטריה, סטטיסטיקה והסתברות, סדרות וחשבון דיפרנציאלי ואינטגרלי (חדו”א). ב-4 יחידות לימוד מתווספות גאומטריה במישור וטריגונומטריה במרחב (וכמו כן החדו”א נראה מקיף יותר), וב-5 יחידות מתווספים וקטורים ומספרים מרוכבים. אני מקווה לכתוב בהמשך פירוט על מה קורה בכל אחד מהתחומים הללו, הן בתיכון והן במתמטיקה “אמיתית”, אבל שוב, הנה תקציר: אף אחד מהנושאים הללו לא נראה לי הכרחי לתלמידים, למעט הסטטיסטיקה וההסתברות שהן משהו שאני סבור שראוי להכיר באופן כללי.

אני אנסה לתת נימוק אחד שלדעתי הוא טוב מאוד לגבי מה מבדיל את המתמטיקה הטרום-תיכונית משאר תחומי הלימוד, ובגללו חשוב מאוד ללמוד אותה. מתמטיקה היא באופן כללי תחום שבו חומר הלימוד בנוי בשכבות, כך שכל שכבה נזקקת לקודמותיה באופן קריטי. מי שאינו שולט בחיבור, לא יוכל לבצע כפל; מי שלא יודע לבצע כפל, יסתבך עם שברים ואחוזים; מי שמסתבך עם שברים יכול לשכוח מפתרון משוואות בנעלם אחד; מי שלא יודע לפתור משוואות בנעלם אחד, יכול לשכוח מחדו”א. אני לא מכיר מקצוע בית ספרי כלשהו שבו המצב דומה. בלימודי היסטוריה, למשל, לומדים על תקופות ואירועים רבים, אבל אם נשכח לגמרי את כל האימפריה הרומית, למשל, עדיין נוכל להבין לא רע את מלחמת העולם השניה. במתמטיקה זה לא כך. המתמטיקה הרבה פחות סלחנית. קפצתם מעגלת המתמטיקה? חלפו שניותיים והנה נשארתם מאחור.

זה אחד ההסברים הנפוצים עבור הקושי של המתמטיקה הבית ספרית. שמעתי סיפורים אישיים עגומים רבים על אנשים שהגיעו למסקנה שמתמטיקה היא לא בשבילם, וברוב המקרים הסיטואציה הייתה דומה - בשלב זו או אחר התלמיד איבד לרגע את החומר, והמורה היה לא סלחן ולא סבלני ולא סייע לו להשלים, ומאותו רגע והלאה הכל היה אבוד והשליטה במתמטיקה מעולם לא חזרה. הייתה לי בעיה דומה עם לימודי שפות - הן בצרפתית והן בערבית בשלב מוקדם כלשהו לא הבנתי את מה שהמורה אמרה, ומאותו רגע והלאה היא הניחה שאני מכיר מילים שלא הכרתי, ולא הצלחתי להבין יותר מה היא אמרה והסוף הגיע חיש קל. אבל בלימודי שפה הסכנה של אובדן מוחלט מצויה בעיקר בתחילת הדרך, כשעוד מחפשים נקודת אחיזה בסיסית; במתמטיקה זה כל הזמן כך. גם במתמטיקה אוניברסיטאית. על כן, אם נוותר על המתמטיקה הטרום תיכונית, אפילו קצת, התלמידים יאבדו את זה, ונקבל מצב שבו אף אחד לא יודע שום דבר במתמטיקה ואין לו יכולת ללמוד מתמטיקה רצינית יותר, או פיזיקה, או כל תחום מדעי אחר שנזקק למתמטיקה, בלי השלמה שתהיה קשה מאוד לביצוע. במתמטיקה תיכונית המצב שונה מכיוון שאת רוב המתמטיקה שם לומדים ממילא מחדש, ברמה גבוהה יותר, באוניברסיטה.

לכן, אם למקד את הדיון, השאלה המרכזית היא למה צריך ללמוד מתמטיקה לבגרות? יותר ספציפית, למה צריך ללמוד דווקא 5 יחידות מתמטיקה לבגרות ולא לקחת את המינימום ההכרחי? השאלות הללו הן תמיד במרכז דיונים סוערים (יחסית, יחסית) ובזמן האחרון במיוחד.

אני אנסה לתת כמה תשובות אפשריות. השאלה המרכזית היא עד כמה המתכונת הנוכחית של לימודי המתמטיקה אכן תואמת את התשובות הללו, והאם אפשר לשנות אותה בצורה שתתאים יותר.

הסיבה הראשונה היא שמתמטיקה חשובה ללימודים ריאליים. ובגרסה קיצוניות יותר, שמתמטיקה הכרחית לשכר גבוה בתעשייה (עד כדי הבאת קורלציות - שמעידות או לא מעידות על גרירה, זה לא הדיון כאן - בין הציון במתמטיקה ובין השכר העתידי, שמביאות לטענות כמו “עדיף לקבל 60 בחמש יחידות מאשר 100 בארבע יחידות”). הסיבה הזו, כמובן, לא אומרת כלום למי שלא רואים את המשך הקריירה ותחומי העניין שלהם בתחומים ריאליים. אבל כמה היא רלוונטית למי שהולכים ללימודים ריאליים? כל מי שלמד חדו”א באוניברסיטה יכול להעיד על כך שחדו”א של תיכון לא ממש דומה. מצד שני, יש כל מני דברים שהמרצים באוניברסיטה יניחו שהסטודנט כבר יודע, למשל נוסחאות טריגונומטריות (שמשתמשים בהן לעתים רחוקות יחסית, אבל משתמשים). אין ספק שאם מבטלים עכשיו חלקים מהבגרות במתמטיקה, זה יכריח את האוניברסיטאות לשנות קצת את הגישה לסטודנטים, ואולי להציע קורס מבוא למתמטיקה (המצב לא שונה עד כדי כך בפועל גם היום; האוניברסיטה הפתוחה מציעה קורס “אשנב למתמטיקה” ובאוניברסיטאות פועלות מכינות שמטרתן בדיוק לתת ידע רלוונטי ברמה קדם-אוניברסיטאית).

אבל השאלה העיקרית כאן, מבחינתי, היא האם שינוי אופי לימודי המתמטיקה כך שיהיה קרוב יותר למה שאני מבין כמתמטיקה “אמיתית” ופחות טכנית יפגע במטרה הזו? מצד אחד, הרמה הטכנית של התלמידים כנראה תהיה פחותה; מצד שני, לא ברור עד כמה השליטה הטכנית הזו חשובה בלימודים האוניברסיטאים; דווקא היכרות עם נושאים נראית לי יותר רלוונטית מאשר ביצוע חישובים סבוכים. מכל מקום, ברור שזה מזמין דיון יותר פרטני שיכנס לפרטים המלוכלכים של חומר הלימודים התיכוני ומה שעושים באוניברסיטה. אני חושב שכולנו נסכים שבשל החשיבות של המתמטיקה בלימודים ריאליים, הרי שמתמטיקה היא בהחלט מקצוע שצריכה להיות בו בגרות, אבל לאו דווקא בגרות חובה. המציאות בפועל של שלוש-ארבע-חמש יחידות כבר מכירה בכך, אבל היא לא הולכת עד הסוף ועדיין מכריחה אנשים לא ריאליים ללמוד ברמת שלוש יחידות. וזה אומר גאומטריה אנליטית וטריגו וחדו”א ברמה כלשהי ואלו, חברים, לא תחומים קלים. אל תתנו למתנשאים על שלוש יחידות לשקר לכם. גם שלוש יחידות מתמטיקה זה לא ממש קל.

סיבה אחרת, ונפוצה למדי, ללימודי מתמטיקה היא שמתמטיקה היא משהו שכל בן תרבות צריך לדעת. חלק מהידע הבסיסי שבית הספר צריך להקנות. לדעתי זה בוודאי נכון עד למתמטיקה התיכונית, וכבר אמרתי זאת קודם; אבל מה עם החומר לבגרות?

בגרויות החובה בישראל הן באזרחות, אנגלית, היסטוריה, לשון, מתמטיקה, ספרות ותנ”ך. שימו לב לכך שהמתמטיקה במיעוט - מלבד אולי לשון, שהיא תחום שקשה לסווג אותו בצורה פשוטה, אין בגרות בשום תחום ריאלי או מדעי. פיזיקה, כימיה, ביולוגיה, מדעי המחשב (ואחרים שאני משמיט) כולם מקצועות בחירה. אם נשמיט את המתמטיקה, נקבל שבגרויות החובה אינן כוללות שום דבר שקשור למדע. בעיני זה מצב בלתי נתפס. אני יכול להבין מדוע קריטי ללמוד לבגרות אזרחות ואנגלית, אבל בנוגע ליתר הבגרויות אני לא רואה הצדקה לכך שהן יהיו חובה, אבל אף מקצוע מדעי לא. אפשר אולי לנהל דיון על ביטול חובת הבגרויות בכלל, אבל זה יהיה דיון רחב בהרבה מהדיון על המתמטיקה.

אולי נכון, אם כן, ללמד מקצוע מדעי אחר שאינו מתמטיקה? פיזיקה, גם ברמה תיכונית, נזקקת ללא מעט מתמטיקה; ביולוגיה וכימיה, פחות. מדעי המחשב מתחלקים לשני היבטים מרכזיים: פרקטיקה של תכנות, ותיאוריה. התיאוריה היא סוג של מתמטיקה (וסוג מעניין למדי) ואני חושב שללמוד תכנות נטו זה פספוס, כך שגם אם נמיר את המתמטיקה בפיזיקה או במדעי המחשב המשמעות תהיה שעדיין לומדים מתמטיקה ברמה כלשהי, פשוט מתמטיקה מסוג שונה. אם כן, אולי צריך להחליף אותה בכימיה או ביולוגיה? אלו תחומים שאיני בקיא בהם מספיק לצורך דיון רציני בעניין, בפרט לא ברמה שבה הם נלמדים בתיכון. אולי דווקא כדאי לעשות זאת. עם זאת, לא ראיתי הצעה כזו בשום מקום בפולמוס המתמטיקה כך שלא אכנס גם לעובי הקורה שלה.

אם כן, אם אנחנו כבר יוצאים מנקודת הנחה שיש איזה שהוא סט בסיס של “דברים שכל בן תרבות צריך לדעת”, אני רוצה שהמתמטיקה תיכנס לשם. לא מסכימים? הייתי מעדיף שתתקפו את הרעיון של סט בסיס כזה מלכתחילה. עוד נחזור לזה אחר כך, כשנדבר על התנגדויות ללימוד מתמטיקה.

מבין הסיבות הנפוצות, המעורפלת ביותר לטעמי היא זו: המתמטיקה מחדדת את המחשבה. זו הרי אמירה מעורפלת לחלוטין. מה זה בכלל אומר, לחדד את המחשבה? אפשר למדוד את זה? אפשר להשוות את זה לחידוד של תחומים אחרים? להכיר את נפתולי מלחמת העולם השניה לא מחדד את המחשבה? להבין את המבנה של השפה העברית? להכיר ניתוחים של התנ”ך? ומה, לא שמענו אינסוף פעמים את טיעוני “מחדד את המחשבה” בהקשר ללימודים תורניים, כתירוץ להתנגדות ללימודי הליבה? מה זה הטיעון הזה?

אם כן, דבר ראשון שצריך לעשות הוא לקחת מהמתמטיקה את המונופול שלה כמחדדת מחשבה. לימודים מרוב הסוגים מחדדים את המחשבה, זו חלק מהפואנטה בלימוד, כל עוד הוא נעשה נכון. אפשר אולי לומר שהיא מחדדת את המחשבה בכיוונים מסויימים שתחומי לימוד “הומניים” יותר לא, אבל צריך להיות זהירים גם כאן. אני מוכן לקבל לגמרי את הטענה שמתמטיקה תיכונית מחדדת את המחשבה, ושמתמטיקה ברמה גבוהה יותר מחדדת את המחשבה, אבל אני חושב שאלו שני חידודים שונים לגמרי. אני חושב שהמתמטיקה התיכונית עושה משהו הרבה פחות מוצלח מאשר מתמטיקה “אמיתית”. כך שגם אם מדברים על חידוד המחשבה, זה לא מצדיק את לימודי המתמטיקה במתכונתם הנוכחית, אלא אולי דווקא מדגיש את הצורך בחידוד נושאי הלימוד. וזה לא מצדיק מתן עדיפות למתמטיקה על פני מקצועות אחרים.

מדוע לא ללמד מתמטיקה?

אם כן, אני חושב שהנימוקים בעד מתמטיקה טרום-תיכונית הם טובים אבל שהנימוקים בעד מתמטיקה לבגרות הם לא חזקים יותר מאשר עבור אף מקצוע אחר. אבל מה עם נימוקים נגד המתמטיקה? ובכן, כאלו אנחנו מקבלים שוב ושוב; רוב המאמרים שיצא לי לקרוא הנוגעים לפולמוס המתמטיקה הם חד משמעית נגדה, לעתים עד כדי דמוניזציה גמורה. שוב, התקציר של דעתי על כלל המאמרים הללו הוא פשוט: הם שופכים את התינוק עם המים. הרי בבירור יש בעיה קשה מאוד עם לימודי המתמטיקה בבית הספר, והם נוקטים בפתרון הפשוט והעצלני של “אז בואו לא נלמד מתמטיקה!” וחסל, במקום לשאול את השאלות החשובות יותר - האם אפשר לשנות את חומר הלימוד? האם יש כאן בעיה שנוצרת בשל מורים לא טובים? שיטות הוראה לא מספיק טובות? מחסור בעזרים חיצוניים? התמקדות מופרזת בתרגול? יצירת תדמית שגויה בציבור? וכו’ וכו’ וכו’. על כל השאלות הללו אפשר לכתוב פוסט נפרד, וגם את זה אולי אעשה. בינתיים בואו ננסה לראות כמה דוגמאות למאמרים אנטי-מתמטיים.

לפני שנתחיל, אני רוצה לסנגר עליהם קצת, כי אחר כך אתרגז עליהם מאוד. המאמרים הללו לא מגיעים מאנשים עצלנים או טיפשים בשום צורה. הם מגיעים משילוב של שתי בעיות - האחת, המתמטיקה הבית ספרית כפי שהיא נלמדת כרגע היא קשה ומייאשת עבור תלמידים רבים; השניה, המתמטיקה מצויירת ביותר מדי מקומות בתור “כרטיס כניסה” לחיים, מה שגורם לאנשים לחוש צורך לציין שהיי, אפשר להיות בן אדם מתפקד ומועיל לחברה גם בלי מתמטיקה (מפתיע!). אלו שתי בעיות רציניות, ולרוב יוצא שהמאמרים מבקרים אותן, אבל זה איכשהו מתערבב בביקורת כללית על המתמטיקה (שבחלק מהמקרים הכותבים כנראה לא מכירים בכלל).

הטיעון הנפוץ ביותר הוא שלימודי מתמטיקה פוגעים בתלמידים בצורה שהיא כנראה קיצונית יותר מכל תחום אחר. הנה מאמר של נועה אסטרייכר שעוסק בסבל הפרטי שלה מלימודי המתמטיקה. זה מתחיל ב”הפסקתי להבין חשבון קצת אחרי שסיימנו ללמוד את לוח הכפל…אולי הוראה מתקנת או תשומת לב נוספת לילדה שנשרכת מאחור היו עוזרות לי לעלות שוב על השביל, אבל במקומם נתקלתי בחומה של בוז: חשבון זה קל, ומי שלא מבין אותו – הוא כנראה טיפש מכדי שיעכבו לכבודו את שאר הכיתה.” ונמשך ב”למרות ההצלחה שלי במקצועות רבים בתיכון, המסר שקיבלתי היה ברור – את לא שווה כלום בלי מתמטיקה” ועובר לקריאה לביטול הבגרות “כאשר הדבר הכרחי לשימור וטיפוח יכולותיו האחרות של התלמיד, במקום להשמיד אותן תחת מכבש הלחצים המתמטי אשר לא מועיל בדבר” (ומסיים ב”די לטרור המתמטי”). והנה מאמר אחר, של רוחמה אלבג, שמתחיל בקריאה לבטל את הבגרות, מדבר על “החרדה המתלווה לבחינה, התסכול והאימה”, ועובר לחוויה האישית של “שיעורי המתמטיקה עיקרו את נפשי. כמעט עזבתי את התיכון, ולא הייתי היחידה”. במאמר אחר, של שלומי ברזל, הוא מדבר על “התחום הדמוני הזה נקרא עדיין חשבון. מתלווה אליו כמובן אחותו המפלצתית הנדסה, שבעוד שנה בערך תתהדר בשם המבעית גיאומטריה.”. ורינת פרימו, בביקורת על “איך בוטלה המתמטיקה” של אביעד קליינברג אומרת ש”המתמטיקה הרסה והורסת להמון ילדים את החיים”. במאמר אחר, אומרת אור סגל ש”בשיעור מתמטיקה הראשון השנה, המורה הודיעה שכדי להצליח בחמש יחידות צריך “לאפסן את החיים בקופסה””. במאמר אחר כותבת ספיר ליפקין ש”לגרום לתלמידים שלא ניחנו בגישה למתמטיקה להזיע מעל דפי התרגול ולבזבז שעות מזמנם בסבל במקום לעודד אותם להתפתח בתחומים שהם מוכשרים בהם זו פשוט התעללות”.

הבנתם את העניין. בכל המקרים הללו הכותבים מדברים בעיקר מתוך החוויה האישית השלילית שלהם, אבל אני חושב שהחוויה הזו אכן מתארת את התחושה של רבים מאלו שמתמודדים עם מתמטיקה בית ספרית. אפשר להגיד שזה המצב ביחס לכל מקצוע בית ספרי, אבל זה לא נכון; אנחנו לא באמת רואים כל כך הרבה מאמרים שמתלוננים על ספרות בצורה שכזו, למשל. ואני באמת, באמת רוצה להבין למה. מה הופך את המתמטיקה לכל כך מפלצתית. עזבו אתכם לרגע מהאופן שבו מפמפמים את החשיבות של המתמטיקה ובחלק מהמאמרים שקישרתי אליהם מתלוננים עליה - למה זה כל כך נורא לתלמידים?

הבלוג הזה מיועד בעיקר לאנשים בעלי ידע כלשהו במתמטיקה על-תיכונית, גם כדי לעזור להם להבין נושאים שהם מתמודדים איתם כרגע, וגם כדי להכיר להם נושאים חדשים. אבל מדי פעם אני כותב פוסט שיש לי תקווה שיהיה מובן גם לאנשים בלי רקע במתמטיקה או נטיה מתמטית. בחלק מהמאמרים שקישרתי אליהם מדברים על כך שאין לכל האנשים “ראש ריאלי” או “חשיבה מתמטית” או מה שזה לא יהיה שמאפשר לאדם להתמודד עם מתמטיקה תיכונית. האם זה אומר שהוא לא יוכל להבין דברים כמו מונטי הול, או את גניבת האסטרטגיה של צ'ומפ, או את חישוב שטח המשולש שהראיתי קודם, או אפילו את המלון של הילברט? קראו לי נאיבי, אבל אני מאמין שאת הדברים הללו יכול להבין גם אדם שמעיד על עצמו שאין לו “ראש מתמטי” כלל. אני מאמין שלרובנו (למעט מקרים קיצוניים באמת) יש יכולת בסיסית להבין רעיונות מתמטיים ואולי אפילו לעשות איתם דברים. זה לאו דווקא כיף לנו ולאו דווקא מעניין, אבל היכולת קיימת. השאלה היא האם היא רלוונטית למה שעושים בבית הספר, או שבבית הספר עושים משהו מאוד ספציפי, שדורש דרישות אחרות מאשר דורשת מתמטיקה “אמיתית” והדרישות הללו הן אכן תובעניות מדי עבור אנשים רבים. הניחוש שלי הוא שהתשובה חיובית. לכן אני חושב שהביקורת של “תשאירו את המתמטיקה רק לאנשים שיש להם את הראש לזה” מפספסת. לפני שזורקים את המתמטיקה לפח צריך לחשוב האם היא חייבת להילמד במתכונת שמוציאה החוצה כל כך הרבה אנשים.

וכל זה, בלי שניכנס בכלל לשאלה האם הבעיה אכן טמונה בכך שאין לאנשים “ראש מתמטי” או במה שהזכרתי קודם - בכך שמתמטיקה היא מקצוע שכל כך קל לאבד אותו בלי סיכוי לחזור לעניינים, ואולי רק אנשים עם “ראש מתמטי” מסוגלים. או לחילופין, מורה פרטי טוב (אבל אני בספק אם מורה פרטי יוכל לסייע בכיתה י’ למישהו שאיבד את זה בכיתה ד’).

טיעון אחר בעד ביטול חובת המתמטיקה הוא ש"הטובים" ממילא יגיעו למתמטיקה. אפשר לראות אותו, למשל, במאמר של גיל גרטל: “כשם שהמתאימים לטיס מוצאים את דרכם להיות טייסים מעולים גם ללא שהיו בהקבצה א’ לטיס בבית הספר היסודי, כך ימצאו לנו המתמטיקאים הדגולים, שיטיסו את האנושות קדימה”. זה טיעון בעייתי משתי סיבות. ראשית, וזו גם מטרת הקמפיין הנוכחי בעד עידוד הלמידה בחמש יחידות מתמטיקה, אנחנו לא רוצים רק את “הטובים”. אין מספיק “הטובים”. אנחנו צריכים הרבה יותר אנשים, גם כאלו שלא יצליחו למצוא את דרכם לבד. שנית, וחשוב יותר, אם אדם כלל לא נחשף למתמטיקה - כלל לא מבין שהתחום קיים, או אם הוא מקבל עליו רושם שגוי לחלוטין - הסבירות שילך אליו תקטן. טיעון דומה קיים גם בספרות, ושם הוא חזק אף יותר - מבלי להיחשף למגוון רחב של יצירות וז’אנרים, איך התלמיד ידע עצמאית מה לחפש? הוא אפילו לא ידע שמשהו חסר לו. אנחנו יכולים אולי להגיד שוב ושוב לתלמיד שמתמטיקה זה מגניב (אבל בפועל מי אומר את זה? טוב, הבלוג הזה מנסה לומר את זה, ואני מקווה שמצליח, אבל קשה לומר שהוא מייצג את החברה) אבל האם זו חשיפה מספקת למתמטיקה?

כמובן, כלל לא ברור שתוכנית הלימודים הנוכחית במתמטיקה מספקת את החשיפה הנכונה; זו עוד המחשה לכך שמה שאמור היה להיות ביקורת (טובה) על תוכן הוראת המתמטיקה הפך לביקורת על עצם לימוד המתמטיקה.

טיעון דומה, ונפוץ ביותר, הוא שרוב התלמידים לא צריכים מתמטיקה. בלשונו של גרטל, “מתמטיקה כמו כל תחום אחר, צריכה להילמד בבית הספר עד רמת הצורך של הלומדים. אצל הרוב המכריע של הילדים מסופק צורך זה במהלך בית הספר היסודי, ואין צורך שמתמטיקה תהייה המקצוע הכי חשוב במערכת החינוך, כמקצוע חובה מעבר לחטיבת הביניים. כמה מאזרחי ישראל חפפו לאחרונה משולשים, חקרו פונקציה ופתרו משוואות דיפרנציאליות? התשובה ברורה, אחוזים בודדים בלבד.” (אגב, אני לא חפפתי משולשים וחקרתי פונקציות מאז התיכון, ומשוואות דיפרנציאליות פתרתי רק בקורס העוסק בכך).

זו בדיוק גישת “המתמטיקה היא ארגז כלים” שהתרעמתי עליה בהתחלה. אפשר להחיל את התלונות הללו על כל מקצוע חובה לבגרות למעט אזרחות ואנגלית (שכן באנגלית רובנו המכריע משתמשים ביום יום, ובאזרחות אנחנו אמורים להשתמש, גם אם איננו עושים זאת). האם הכרת הסיבות לעליה השניה מסייעת לנו ביום יום, למעט בויכוחים אינטרנטיים (ותאמינו לי, גם ידע מתמטי יסייע לכם בויכוחים אינטרנטיים, אתם רק צריכים למצוא את המקום הנכון להתווכח בו)? ודין שור שנגח? והכניסי תחת כנפך? והיכרות עם בג”ד כפ”ת (אלא אם אתם מהאנשים המוזרים שרוצים לכתוב ולדבר בצורה תקנית בעברית, וזה חריג בדיוק כמו חובבי המתמטיקה)? הבנתם את הרעיון. שימושיות היא לא מדד טוב למקצועות החובה לבגרות, בטח לא שימושיות של חומר לימוד ספציפי כמו חפיפת משולשים. אם רוצים לתת טיעון בעד השימושיות, לרוב הוא יהיה משהו אמורפי יותר, איזו סגולה טמירה שלימודים הומניים מחדירים בתלמידים אבל לימודי מתמטיקה לא - מין הפוך-על-הפוך של טיעון “מחדד המחשבה” המתמטי (זה לא כל כך מפתיע שיש לטיעונים בעד טיעוני מראה שהם נגד). במאמר של אלבג נאמר “ישבתי וקראתי בספריה ועולמי נפתח - ויתרתי על חישוב קודקודים והתוודעתי לגיבוריה האלמותיים של האנושות. התמסרתי למחשבות, לרעיונות, לעולם רוחני שהיה מתוק פי כמה ממשוואה עם נעלם אחד או שניים או כמה יש שם, לעזאזל?”.

אם כן, מדוע מודדים את ה”שימושיות” בצורה שונה שכזו? האם בגלל שכל מה שלומדים בבית הספר לא מתחבר ולא יכול להתחבר לתמונה גדולה כלשהי?

אז מה צריך לעשות?

הפתרון הקל מבחינתי הוא לומר “לבטל את חובת הבגרות במתמטיקה ולהשאיר רק מתמטיקה חמש יחידות בתור מקצוע בחירה”. זה יציל את כל שונאי המתמטיקה מלסבול בגללה בתיכון ולהרגיש שהם חסרי ערך כי אין להם בגרות במתמטיקה (ולכן אין להם בגרות בכלל). האם זה באמת פתרון? זה לא ישנה את מעמדן (המוצדק או לא) של חמש יחידות מתמטיקה בתור “כרטיס כניסה” לחיים, או לפחות למעמד סוציואקונומי מסויים. האוניברסיטאות ימשיכו לתת בונוס לספי הכניסה לפקולטות מסויימות עבור מי שיש לו בגרות במתמטיקה (ובצדק, מבחינתן). מי שהיו ניגשים לשלוש יחידות בגרות כנראה יוותרו ברובם על המקצוע, וככל הנראה יהיה להם קשה להשלים אותו אחר כך אם יצטרכו; והאחרים יעברו למה שהיום הוא חמש יחידות ויהיה להם קשה שם. בקיצור, קשה.

אתגר אחר הוא להפוך את לימודי המתמטיקה התיכונית ליותר נגישים, למשהו שרוב התלמידים יכולים להתמודד איתו בלי טראומה. יש כאן שני דברים לפחות שיהיה צורך לטפל בהם: הראשון הוא חומר הלימוד של המתמטיקה התיכונית עצמה, אבל השני הוא החשוב יותר לדעתי - יהיה הכרחי להבטיח שתלמידים לא מגיעים לתיכון כשהם כבר “שרופים” מבחינת המתמטיקה ולא מסוגלים להתמודד עם איזה חומר שלא יהיה שנזרוק עליהם. כפי שאמרתי קודם, שריפה כזו יכולה לקרות בכל שלב, בגלל תלמידים שמאבדים את החומר לרגע ואז לא מצליחים להשלים אותו יותר. איך פותרים את זה?

התשובה הראשונה היא “מורים טובים”. אין ממש מה לעשות בנוגע לכך - מורים טובים הם הדבר החשוב ביותר במערכת החינוך. גם תוכנית הלימודים הטובה ביותר כנראה לא תעבוד אם המורה שמעביר אותה עושה את זה רע. אבל אין מה לעשות, לא תמיד יהיו מורים טובים - מבחינתי זו הנחת יסוד. לכן צריך לדאוג לתלמידים ל”רשת ביטחון” כלשהי. דרך כלשהי לסייע להם ללמוד מתמטיקה בלי להיות תלויים במורה זה או אחר. מה שכיום מושג על ידי מורה פרטי עבור חלק מהתלמידים, ספציפית כאלו שהוריהם יכולים להרשות דבר כזה; זה בדיוק האפקט שאנחנו לא רוצים, אלא משהו שיעבוד “לכולם”. ספרים ולומדות ממוחשבות לעבודה עצמית נשמעים כמו דבר סביר, אבל איך מכריחים את התלמידים לעשות אותם? זה עדיין ידרוש פיקוח מצד בית הספר. הייתי רוצה לומר שאפשר לגרום לתלמידים להתעניין באופן עצמאי, אבל האם אפשר לעשות כזה דבר בכלל? הנה לכם אתגר: האם אפשר לגרום לתלמידים בגילאי יסודי-חטיבת ביניים להתעניין במתמטיקה שהם לומדים? אני לא יודע; עבורי הגילאים הללו הם חור שחור. הבלוג משמש, לשמחתי, בתור “רשת הצלה” עבור סטודנטים באוניברסיטה בקורסים מסויימים (למרות שהוא לא נועד להחליף ספרי לימוד, אבל בתור חומר משלים שמיועד לשפר את ההבנה אני שמח לומר שהוא עובד, לפעמים, בתחומים מסויימים; אם אני גאה במשהו, זה בכך). אבל כתיבה עבור סטודנטים באוניברסיטה היא קלה; ילדים הם אתגר גדול בכמה סדרי גודל, למרות שהמתמטיקה היא לכאורה פשוטה יותר. מי שכבר הרים את הכפפה היה פרופ’ רון אהרוני מהטכניון, שכתב ספרי “חשבון להורים” ו”אלגברה להורים” שמאפשרים להורים עצמם להיות רשת ביטחון עבור הילד. הספרים הללו היו הצלחה יחסית; ייתכן מאוד שזה בדיוק הכיוון שבו צריך ללכת. כיוון אחר הוא לומדה ממוחשבת - בימינו זה יהיה אתר אינטרנט (בתקווה נגיע יום אחד לכך שלכל התלמידים יש גישה לאינטרנט, לכל הפחות מבית הספר), משהו בסגנון Khan Academy אולי? צריך שיהיו בו סרטונים, ומלל כתוב, ותרגילים אינטראקטיביים. וכמובן, בעברית ומתאים לישראל. ורצוי שיהיה כיפי ומעניין. כל זה אפשרי, בתיאוריה; בפועל מישהו צריך להרים את זה ולקדם את זה ולהפוך את זה לסטנדרט.

וכן. אולי צריך לשנות גם את תוכנית הלימודים. אבל כשבאים להציע הצעות כאלו, אנחנו מתנהגים כמו פיל בחנות חרסינה. יש סיבות למה דברים נמצאים בתוכנית הלימודים, ואנחנו לרוב מציעים גזור-העתק-הדבק גסים שלא מודעים לסיבות הללו. זה לא אומר שלא עושים את זה - השמועות שאני שומע הן שתוכנית הלימודים בישראל אכן הולכת לקראת שינוי כלשהו.

אם בכל זאת הייתי נותן דרור לדמיון ומעלים עין מההשלכות, נראה לי שהדבר הראשון שהייתי חושב לשנות הוא את לימודי החדו”א בבתי הספר. כרגע החומר נלמד ברמה מאוד נמוכה ומאוד טכנית, ואני לא בטוח עד כמה זה הכרחי אפילו בתור הכנה לאוניברסיטה. האם ניתן ללמד חדו”א בצורה יותר רצינית, עם יותר דגש על הבנה של המושגים (הקשים) שבבסיסו, מבלי להגדיל את הקושי הטכני? שאלה טובה.

תחומים נוספים שלדעתי צריך לשנות, אולי לקצץ, הם גאומטריה אוקלידית וטריגונומטריה - שניהם חשובים מאוד, אבל מסיבות שונות. טריגונומטריה היא כלי טכני בסיסי שמשתמשים בו בכל תחומי המתמטיקה, אבל הוא גם דוגמה קלאסית לסיפור רהיט האיקאה שהבאתי קודם - בתיכון לא ממש עושים בו שימוש אלא רק מתאמנים על לסובב שוב ושוב ושוב את המברג, עם שלל נוסחאות מפחידות למראה שלאף אחד לא ברור מאיפה הן הגיעו. גאומטריה אוקלידית היא סיפור שונה לגמרי כי היא אולי התחום היחיד שדורש יצירתיות כלשהי, ומלמד את התלמידים איך נראית הוכחה מתמטית אמיתית, ואלו דברים חשובים ביותר - אבל אלו דברים שלטעמי צריך לראות בתחומים רבים יותר, ומתישהו הגאומטריה ממצה את האפקט הזה שלה ואנחנו נשארים שוב עם ערימה גדולה של משפטים שצריך להכיר ולא יהיו שימושיים יותר מדי לשום דבר בהמשך.

והאם צריך להוסיף משהו? יש שני תחומים שקופצים לי מיידית לראש - תורת הקבוצות, וחשבון מודולרי. בשני המקרים צריך להיות מאוד זהירים - אם מלמדים את תורת הקבוצות צריך להיות מאוד קונקרטיים ולחלוטין לא להציג אותה בתור “הבסיס למתמטיקה” או כל מני דברים דומים שאין בהם שום טעם בשלב הזה. עדיין, אני מאמין שאפשר להסביר מושג כמו יחס שקילות כבר בתיכון (בפרט אם לומדים חשבון מודולרי, שם הוא צץ מעצמו), ואפשר אפילו להסביר את האלכסון של קנטור. האם גם אפשר לבחון על הנושאים הללו? שאלה קשה יותר. בחשבון מודולרי אני מאמין שאפשר להסביר נושאים כמו האלגוריתם האוקלידי ומשפט השאריות הסיני ואולי אפילו להגיע לתיאור משהו כמו RSA. האם התחושה שלי מבוססת? קשה לי לדעת. כבר שמעתי סיפורי זוועות על נסיונות ללמד את תורת הקבוצות בבתי הספר וכשלונות חרוצים של הנסיון הזה, אבל האם זה נבע מאופי ספציפי של אופן הלימוד, או מכך שתורת הקבוצות היא חומר “בלתי נגיש” לתלמידי תיכון? לא יודע. זה מצדיק דיון רציני שעומד בפני עצמו; כרגע אני סתם זורק רעיונות.

הפוסט הזה, כאמור, אמור לשמש בתור נקודת התחלה, לא סיום. אני מתאר את המצב כפי שאני מבין אותו - ואני מבין היטב שאני לא באמת מבין אותו. האם ניתן להשתמש בנקודת ההתחלה הזו כדי להגיע אל משהו? תגידו לי אתם.