האם תלמידה גילתה משפט חדש בגאומטריה אוקלידית? (לא, אבל זה עדיין נחמד)

הנה סיפור יפה על איך ראוי, לדעתי, ללמד וללמוד מתמטיקה בבית הספר התיכון: תמר ברבי, תלמידת כיתה י’, הכינה שיעורי בית בגיאומטריה ושמה לב לכך שאפשר לפתור את אחד התרגילים בדרך נוספת. היא הציגה את הדרך הזו בכיתה והמורה העיר שמשפט שעליו היא הסתמכה בדרך הזו לא באמת קיים, ועודד אותה לנסות להוכיח את המשפט הזה. היא ניסתה ומצאה הוכחה. ככה בדיוק צריך לעשות, במקום לומר דברים כמו “המשפט הזה לא בחומר הלימוד ולכן אי אפשר להשתמש בו וזהו” (אם כי למרבה הצער, אם התלמידה תנסה להשתמש במשפט הזה בבחינת הבגרות זה כנראה לא יגמר טוב).

לצערי, זו לא הסיבה שבגללה אני מספר את הסיפור. מה שעשו התלמידה והמורה הוא אחלה וראוי לכל שבח, אבל לא חריג או יוצא דופן עד כדי כך. אני מספר את הסיפור כי הוא הגיע לתקשורת, וזו כהרגלה עשתה ממנו מטעמים. למען האמת, חשבתי שאוכל להתחמק מלכתוב פוסט על העניין (למרות שפוסטים כאלו תמיד מושכים המון אנשים לבלוג), אבל הרבה אנשים ביקשו התייחסות אליו, וזו הזדמנות טובה לדבר על גאומטריה אוקלידית, והיום יום פאי, אז למה לא.

נתחיל מהשורה התחתונה לפני שניכנס למתמטיקה. בידיעה ב”ישראל היום” תואר הסיפור כאילו ברבי “פיתחה משפט חדש בגיאומטריה”. בפועל המשפט אינו חדש ומופיע בספר החשוב ביותר שנכתב אי פעם על גאומטריה אוקלידית: “יסודות” של אוקלידס (ספר 3, טענה 9), עם הניסוח וההוכחה של ברבי (עד כדי הבדלים לא מהותיים שאתייחס אליהם בהמשך). עד כמה שאני רואה, הוא לא מופיע בחומר הלימוד לבית הספר, ואני (שלא קראתי את “יסודות” בצורה מעמיקה אף פעם) לא ידעתי שהוא נמצא שם, כך שדי ברור לי איך התקבל הרושם שהמשפט הוא “חדש”. ברבי והמורה שלה ניסו למצוא מקום שבו המשפט נמצא ופנו למספר מרצים שלא הכירו אותו; עבור ישראל היום זה כנראה הספיק כדי להכריז בביטחון שהמשפט הוא חדש. עיתונות לא ידועה בסטנדרט הגבוה שלה של בדיקת עובדות, ואין כאן שום דבר חדש.

חשוב לי להדגיש פה במפורש שאני לא מנסה למתוח ביקורת על ברבי או המורה שלה. אני מאמין שברבי אכן חשבה על המשפט ועל הוכחתו לבד, ושזה ממש יפה. לנסח ולהוכיח עצמאית משפט מ”יסודות” זה מגניב. מאז שהסיפור התפרסם ראיתי הרבה תגובות שמנסות לומר שנו באמת מה הביג דיל זה משפט ממש טריוויאלי (ועוד תגובות שממש יורדות לפסים אישיים ומשמיצות את ברבי - מה לעזאזל, אנשים). באמת שנפלא מבינתי מה הקושי להכיר בכך שזה לא משפט חדש ועדיין שמדובר על הישג יפה. נכון, אני מאמין ומקווה שאפשר להגיע למצב שבו רוב התלמידים יוכלו לעשות דברים כאלו; ונכון, יש תלמידות כיתה י’ שכבר לומדות מתמטיקה באוניברסיטה ואפילו מתעסקות במחקר מקורי (הכרתי אחת כזו) והיה ממש נחמד אם היו כותבים בעיתון גם עליהן, אבל אנחנו לא בתחרות. יותר מזה, אפילו על “ישראל היום” אני לא ממש כועס - הם טרחו והביאו את הניסוח של המשפט (עם טעות בניסוח שבגוף הכתבה אבל מילא). אולי זה יגרום למישהו להתעניין בגיאומטריה! בקיצור, אם היה כאן פשע תקשורתי, זה פשע נטול קורבן. מזכיר את הסיפור על הנער שגילה “שגיאה” במוצג מתמטי במוזיאון, שכבר סיפרתי בבלוג.

יש עוד נקודה שאני רוצה להתייחס אליה, בהקשר של גילוי משפטים חדשים במתמטיקה. במקרה הספציפי שלנו המשפט מופיע כמות שהוא ב”יסודות”, אבל יש משפטים במתמטיקה שלא מופיעים במפורש בשום מקום עם שם יפה והוכחה מסודרת. יש דברים שהם בגדר פולקלור מתמטי שהעוסקים בתחום מכירים ולא טרחו לכתוב מאמר שמתאר במפורש, אלא הם רק משתמשים בו פה ושם. יש תוצאות שמופיעות בשלל ספרי לימוד בתור תרגיל אבל אף אחד לא טרח לכתוב במפורש בתור משפט (חוץ מהכותב הפדנט ההוא שכתב ספר עב כרס במיוחד עם הוכחות לכל דבר אפשרי ואף אחד לא קרא אותו ולכן לא מביאים אותו בתור רפרנס). ככה זו המתמטיקה - יש המון תוצאות אפשריות, ולכתוב במפורש את כולן לוקח זמן ומקום וקשב. ספרי לימוד מראים תוצאות בסיסיות ומרכזיות, ומשאירים לקוראים לחשוב על היתר (עצמאית, או בעזרת תרגילים) בהתבסס על מה שהם ראו. אם כן, השאלה הרלוונטית עבור המשפט של ברבי היא לא “האם המשפט כתוב איפה שהוא במפורש” אלא “האם המשפט ניתן להסקה בקלות מחומר הלימוד הקיים”, והתשובה לשאלה הזו חיובית. כלל אצבע סביר הוא שכל תוצאה שניתנת להסקה פשוטה כזו, והיא שימושית ומעניינת, כנראה שכבר חשבו עליה בעבר (ובדיונים על המשפט אכן ראיתי צילומי מסך של תרגילים שמדברים על התוצאה הזו). לכן אני אומר שכדאי תמיד לצנן את ההתלהבות לגבי “משפטים חדשים” כל עוד אין בהם תוכן עמוק כלשהו שחורג מהידע הקיים.

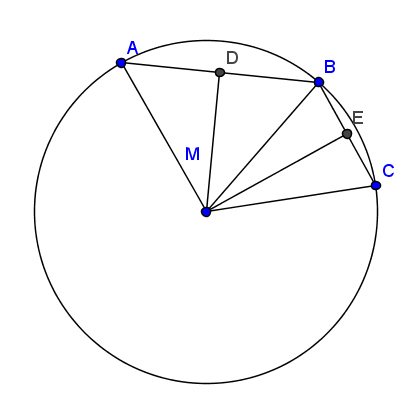
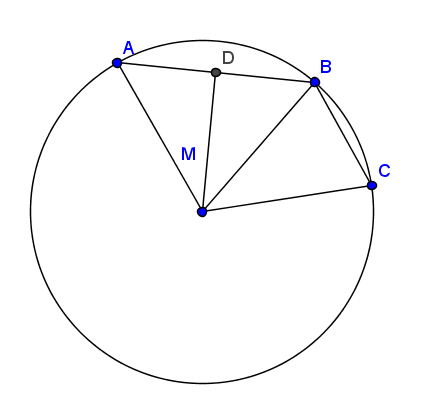
בואו נעבור לדבר על מה המשפט אומר בעצם ואיך מוכיחים אותו. נניח שיש לנו מעגל, ויש לנו שלוש נקודות שונות עליו \( A,B,C \). ונניח שיש נקודה \( M \) שהמרחק שלה משלוש הנקודות \( A,B,C \) שווה, אז \( M \) בהכרח חייבת להיות מרכז המעגל הזה. בניסוח של ברבי: “אם מנקודה יוצאים שלושה או יותר קוים שווים אל היקפו של מעגל, אז הנקודה היא מרכז המעגל והישרים הם רדיוסיו”, ובניסוח של אוקלידס, מתורגם לאנגלית: “If a point is taken within a circle, and more than two equal straight lines fall from the point on the circle, then the point taken is the center of the circle.’’. בניסוח שקול, הטענה פה היא שהמעגל החוסם את המשולש \( ABC \) הוא יחיד, ובניסוח נוסף: לא קיימות שתי נקודות שונות במישור שמרחקן משלוש נקודות נתונות שאינן על קו אחד הוא שווה. 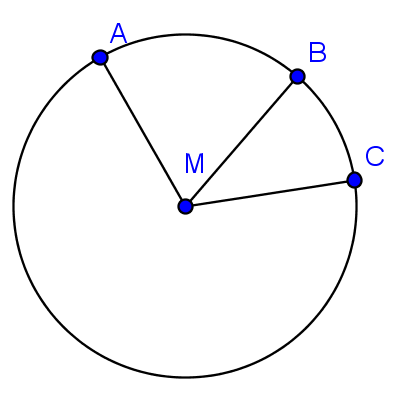מכל הניסוחים הללו, מה שתלמידי בית ספר נתקלים בו הוא זה על כך שהמעגל החוסם את \( ABC \) הוא יחיד. אלא שבכל רשימות המשפטים שיצא לי להציץ בהם, וממה שאני זוכר, הטענה הזו ניתנת בצורה מובלעת לגמרי: כשמתחילים ללמד תלמידים על מעגלים שחוסמים משולשים, מראש מדברים על המעגל שחוסם את \( ABC \), בה’ הידיעה. כלומר, רומזים לכך שהוא יחיד, אבל לא מראים הוכחה לכך או אפילו מציינים זאת במפורש בתור משפט. אבל אם תחשבו על זה לרגע, תראו שאכן הטענה הזו היא המשפט של ברבי ואוקלידס, בלבוש טיפה שונה. כי אם מרחק \( M \) מ-\( A,B,C \) הוא שווה, אז אפשר להעביר מעגל שמרכזו ב-\( M \) ורדיוסו כאורך הקטע \( AM \), והמעגל הזה יעבור דרך כל שלוש הנקודות \( A,B,C \) ולכן יחסום את המשולש \( ABC \). מכיוון שיש רק מעגל אחד שחוסם את \( ABC \) זה יהיה המעגל שהתחלנו ממנו. זו הסיבה שבגלל גם אם המשפט לא היה מופיע אצל אוקלידס בניסוח הזהה לזה של ברבי, לא היה במשפט חידוש של ממש. מה שנחמד הוא שברבי הוכיחה את המשפט בלי להעזר בטענה על כך שהמעגל החוסם הוא יחיד.

על פניו, נראה שהניסוח של אוקלידס הוא פחות כללי כי הוא מניח שהנקודה \( M \) נמצאת בתוך המעגל. האם זה אכן ניסוח פחות כללי? על פניו נראה לי שזה לא ניסוח פחות כללי. אני לא רואה שאוקלידס נעזר בהנחה הנוספת הזו במהלך ההוכחה, כך שנראה שהוא פשוט מציין עובדה, שכפי שההוכחה מראה היא אכן נכונה - הנקודה \( M \) חייבת להיות בתוך המעגל. זה מובלע גם בניסוח של ברבי: נניח ש-\( M \) היא נקודה כלשהי שמרחקה מ-\( A,B,C \) שווה, אז נובע מכך שהיא מרכז המעגל ולכן בפרט היא חייבת להיות בתוכו. כך שהסיטואציה הנוספת של “\( M \) אינה בתוך המעגל ועדיין מרחקה מ-\( A,B,C \) שווה” שנראה שברבי מטפלת בה ואוקלידס לא אינה יכולה להתקיים כלל.

עדיין, צריך להיות מאוד זהירים עם קביעות נחרצות כאן. למה? ובכן, כי גיאומטריה אוקלידית היא תחום ערמומי וחמקמק ממה שנראה במבט ראשון, ומה שנראה לנו בתור הוכחה לגיטימית לחלוטין עשוי להתגלות כמשהו שגוי שנסמך על הנחות סמויות שלנו שאנחנו משתמשים בהן באופן מובלע. “יסודות” הוא טקסט מונומונטלי ואולי הטקסט המשפיע ביותר אי פעם על המתמטיקה כפי שאנו מכירים אותה כיום, אבל גם הוא לא חף מבעיות כאלו. אולי ההנחה לגבי כך ש-\( M \) בתוך המעגל כן באה לידי ביטוי בצורה שאני מפספס; אולי משהו חסר בהוכחה של ברבי כי היא לא משתמשת בהנחה הזו; ייתכן. אבל אני חושב שההנחה הזו לא נדרשת להוכחה של אוקלידס ולכן שהמשפט שאוקלידס מוכיח זהה למשפט שברבי מוכיחה.

איך הולכת ההוכחה? מכיוון שההוכחות של ברבי ואוקלידס הן אותו הדבר אציג את שתיהן ביחד. ההוכחה אצל ברבי קצרה יותר כי היא משתמשת במשפטים סטנדרטיים שנלמדים בשיעורי הגיאומטריה בימינו; אוקלידס מפרט טיפה יותר (תוך שימוש במשפטים בסיסיים יותר). את הרעיון בשתי ההוכחות אפשר לסכם כך: נבנה את המיתרים \( AB \) ו-\( BC \) של המעגל ונראה שהאנכים האמצעיים שלהם נפגשים ב-\( M \). בואו נזכיר מה כל זה אומר. “מיתר” במעגל הוא קטע שמחבר שתי נקודות שעל המעגל. “אנך” לקטע הוא קטע שנחתך איתו ויוצר זווית של 90 מעלות בנקודת החיתוך. “אנך אמצעי” הוא אנך לקטע שחותך אותו בדיוק באמצע הקטע (“קטע” הוא קו ישר עם נקודות קצה).

שתי ההוכחות נסמכות על הטענה הבאה, שאוקלידס מוכיח יותר מוקדם והיא חלק סטנדרטי מחומר הלימוד בתיכון בימינו: אנך אמצעי למיתר במעגל עובר דרך מרכז המעגל. כשלומדים את המשפט הזה בתיכון הוא עשוי להיראות (כפי שרוב המשפטים בגיאומטריה נראים) כמו אוסף אקראי של מילים שלא ברור מה הפואנטה שלו. אצל היוונים כל העניינים הללו היו “חיים” יותר מאצלנו כי הם שיחקו משחקים - הם ניסו לבנות דברים שונים ומשונים בעזרת סרגל ומחוגה. בפוסט שלי על משחק שבו עושים בדיוק את זה הופיע גם שימוש של המשפט הזה: כשהיה נתון לי משולש ורציתי לבנות את המעגל החוסם שלו. לצורך כך צריך למצוא את נקודת האמצע של המעגל (ואז משתמשים במחוגה שנחה על נקודת האמצע הזו ועל אחד מקודקודי המשולש). מה עשיתי שם? מצאתי את נקודות האמצע של צלעות המשולש (שהן בעצם מיתרים במעגל שאני מנסה לבנות), העברתי לכולן אנך דרך נקודות האמצע הללו, והמקום שבו כל האנכים הללו נפגשו (בעצם מספיק רק שני אנכים) חייב להיות מרכז המעגל, כי כל אחד מהאנכים עובר דרך מרכז המעגל, ולכן אם יש להם רק נקודה משותפת אחת, היא חייבת להיות המרכז הזה.

הנה איך שההוכחה עובדת. גם ברבי וגם אוקלידס בונים את המיתר \( AB \) ואז מורידים אליו קטע מ-\( M \); נקרא לנקודת החיתוך של הקטע עם \( AB \) בשם \( D \):

ההבדל הוא שאוקלידס אומר שהוא מוריד תיכון (כלומר, קטע שחוצה את \( AB \) לשניים: \( AD \) שווה באורכו ל-\( DB \)) ואילו ברבי מורידה אנך (הקטע \( MD \) מאונך לקטע \( AB \)). הפואנטה של שניהם היא שבמשולש \( AMB \), התיכון הוא גם אנך. כדי להראות את זה ברבי משתמשת במשפט על כך שבמשולש שווה שוקיים הגובה לבסיס הוא גם תיכון (המשולש \( AMB \) הוא שווה שוקיים כי על פי ההנחה הבסיסית, \( AM \) שווה באורכו ל-\( BM \)); אוקלידס לעומתה לא מניח משפט קודם על אנכים ותיכונים אלא מוכיח בצורה מפורשת: הוא אומר שהמשולש \( ADM \) חופף למשולש \( BDM \) על פי צלע-צלע-צלע: \( AM=BM \) זו ההנחה הבסיסית; \( AD=BD \) על פי זה שאוקלידס בנה תיכון; ואילו \( MD \) היא צלע משותפת. המסקנה של אוקלידס היא שהזוויות \( \angle ADM \) ו-\( \angle BDM \) הן שוות, ומכיוון שהן משלימות ל-180 מעלות, הן בנות 90 מעלות כל אחת, ולכן קיבלנו אנך.

את אותו הדבר אפשר לעשות גם עבור המשולש \( BMC \), ולקבל עוד אנך אמצעי למיתר שעובר דרך \( M \). קיבלנו שני אנכים אמצעיים למיתרים שונים שנקודת החיתוך היחידה שלהם היא \( M \), וזה מסיים את ההוכחה.

שימו לב שההוכחה הזו מקפלת בתוכה גם את ההסבר למה אנך אמצעי למיתר עובר דרך מרכז המעגל. מה בעצם קרה פה? לקחנו נקודה \( M \) כלשהי שהמרחק שלה מ-\( A \) שווה למרחק שלה מ-\( B \), והוכחנו שהנקודה הזו נמצאת על האנך האמצעי למיתר \( AB \). זה אומר שכל הנקודות שמרחקן מ-\( A \) שווה למרחקן מ-\( B \) נמצאות על האנך הזה. בפרט מרכז המעגל שעובר דרך \( ABC \) חייב להיות עליו (בין אם הוא \( M \). ובין אם הוא נקודה אחרת).

אז אם לסכם: לא, אין כאן תגלית חדשה במתמטיקה. כן, יש כאן סיפור יפה על תלמידה ומורה שנותנים דוגמה לאופן שבו לימודי מתמטיקה בבית הספר יכולים להיות מגניבים. כן, יש כאן הזדמנות לדבר על מתמטיקה תיכונית בצורה מעניינת. לא, אני לא מתלונן.