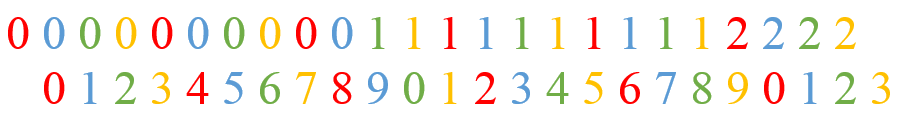על מספרים שאינם ניתנים למציאה בפיתוח העשרוני של 1/998001 ושברים דומים

המניע לפוסט הזה הוא וידאו של נמברפיל שאותו לא ראיתי וכרגיל בעניינים הללו אדבר כאן כאילו הוא לא קיים בכלל. הוא עוסק בקסם מתמטי נפלא, מהסוג שאפשר להסביר פחות או יותר לכולם (והפוסט הזה ינסה להיות נגיש לכולם, ואם אתם “כולם” ולא הבנתם אתם בהחלט מוזמנים להגיב בתגובות ואנסה לתקן). מה הקסם? בואו ניקח את השבר \( \frac{1}{998001} \) ונכתוב אותו בתור שבר עשרוני. נקבל:

\( \frac{1}{998001}=0.000001002003004005006007008009010011012013014\dots \)

מה הולך פה? השבר הוא מהצורה אפס-נקודה ואז הרבה ספרות שכדאי לחלק אותן לשלשות. השלשה הראשונה היא 000; השניה היא 001; השלישית היא 002 וכן הלאה. אני מסיים עם שלוש נקודות, אבל זה לא נגמר שם: זה ממשיך וממשיך וממשיך והנה הספרות האחרונות:

\( \dots9990991992993994995996997999\dots \)

זה לא מסתיים גם אחרי ה-999 שבסיום - זה פשוט מתחיל לחזור על עצמו (מתחילים שוב מ-000). אנחנו מקבלים פה שבר עשרוני מחזורי שמורכב מכל השלשות האפשריות של ספרות בין 0 ל-9, כשהן מסודרות לפי הסדר, למעט יוצא מן הכלל אחד: אם תשימו לב, 998 חסר פה. מ-997 עוברים הישר אל 999. זה גם הדבר היחיד שחסר פה.

אם אתם לא אוהבים מספרים או מתמטיקה או סתם תעלומות מתח בלשיות, כנראה שזה לא יעניין אתכם. אותי זה מעניין: מייד קופצות לי לראש כמה שאלות:

1. למה 998 חסר? מה הולך פה? איך זה ייתכן שכולם פה ורק הוא לא?
2. מה כל כך מיוחד ב-998001 שדווקא הוא מניב את הסדרה הקסומה הזו?
3. האם אפשר גם להניב סדרות של זוגות במקום שלשות, או רביעיות, או כל דבר אחר? איך?
4. האם זה עובד רק בבסיס 10 או שזה יעבוד בכל בסיס ספירה אחר (דהיינו, אם נשתמש במספר גדול יותר או פחות של ספרות מאשר עשר הספרות שאנו רגילים אליהן)?
5. האם אפשר לייצר עוד תבניות מעניינות בפיתוח העשרוני של מספרים?

בפוסט הזה אני אענה לשאלות הללו. התשובה ל-1 קצת מסובכת, אבל הנה התשובות המהירות לכל היתר: מה שמיוחד ב-998001 זה ש-\( 998001=\left(999\right)^{2} \). סדרה של זוגות אפשר להניב עם \( 99^{2} \), סדרה של בודדים (כלומר, \( 0.12345679\dots \)) אפשר להניב עם \( 9^{2} \), סדרה של רביעיות עם \( 9999^{2} \) וכן הלאה. זה עובד בכל בסיס: אם יש לנו \( d \) ספרות בבסיס הספירה שלנו, אז נצטרך להשתמש במספרים שהם חזקות של מספר שהוא סדרה של חזרות על הספרה \( d-1 \). ואפשר לייצר המון תבניות מעניינות בפיתוח העשרוני של מספרים - למעשה, אפשר לייצר כל תבנית, ולכן מה שמעניין פה הוא השאלה אילו תבניות מעניינות אפשר לייצר כשהמונה הוא 1.

מה שנחמד פה הוא שהתשובות הללו לא באמת מספקות. אני עדיין רוצה להבין למה זה קורה, ואיך אפשר להוכיח שזה קורה, וכדומה. לצורך כך עדיף להתרכז קודם כל במקרה הפשוט יותר: \( \frac{1}{81}=0.12345679\dots \). כאן יש לנו בעצם את אותו רעיון - קיבלנו את סדרת כל המספרים מ-0 עד 9, רק ש-8 משום מה נעדר, ואז הסדרה מתחילה מחדש. אחרי שנבין מה הולך במקרה הזה, יהיה קל להבין גם מה קורה במקרה של \( \frac{1}{998001} \).

עכשיו אפשר לתת הסבר קצר יחסית לסיפור הזה, אבל הוא יניח ידע קודם גם על מה זה פיתוח עשרוני וגם על משהו מחשבון דיפרנציאלי. אז בואו נחלק לפרקים ומי שרוצה את ההסבר, שידלג לפרק המתאים (שנקרא “ובחזרה לבעיה המקורית…”).

מה זה פיתוח עשרוני?

יש כל מני דרכים לתאר מספרים. את המספר “שבעה עשרה” אפשר לכתוב כך: XVII. זו השיטה שבה הרומאים השתמשו והיא איומה ונוראה. אנחנו, בימינו, אוהבים לכתוב אותו כך: 17. כלומר, את הספרה 1 ומימינה את הספרה 7. “אחד-שבע”. הגאונות בשיטה שלנו נעוצה בכך שה-1 שמופיע שם לא מתאר את המספר “אחד”; הוא מתאר את המספר “עשר”. 17 הוא בעצם תרגיל חשבוני: עשר-ועוד-שבע. למעשה, התרגיל מסובך טיפה יותר מכך: למשל, 27 הוא התרגיל “שתיים כפול עשר ועוד שבע כפול אחד” ואילו 103 הוא התרגיל “אחד כפול מאה ועוד אפס כפול עשר ועוד 3 כפול אחד” וכן הלאה. כל מספר שנכתב בשיטה העשרונית הוא בעצם סכום של חזקות של 10, כשהספרות שנכתבות אומרות לנו כמה פעמים לקחת כל חזקה. כלומר, \( 123 \) הוא כתיב מקוצר עבור הסכום \( 1\cdot100+2\cdot10+3\cdot1 \), ואם אני אשתמש בשיטת הסימון המקובלת שלנו לחזקה, אני אקבל את הכתיב \( 1\cdot10^{2}+2\cdot10^{1}+3\cdot10^{0} \).

הסיפור הפשוט והנחמד הזה הופך למסובך הרבה יותר כשאנחנו רוצים לתאר שברים. הרעיון הבסיסי נשאר זהה: אנחנו עדיין כותבים סכום של חזקות של 10 כשהן מוכפלות במקדמים. העניין הוא שעכשיו החזקות של 10 יכולות להיות חזקות שליליות. חזקה שלילית של 10 היא בעצם חזקה חיובית של 1 חלקי 10: \( 10^{-1}=\frac{1}{10} \) ו-\( 10^{-2}=\frac{1}{100} \) ובאופן כללי, \( 10^{-n}=\frac{1}{10^{n}} \). זו פשוט ההגדרה של חזקה שלילית. כעת, מוסכמת הכתיבה שלו של מספרים היא שאם אנחנו קוראים מספר מימין לשמאל אז הספרה הימנית ביותר היא ספרת האחדות, זו שמשמאלה היא ספרת העשרות, וכדומה. כלומר, הספרה הימנית ביותר היא בדרך כלל הספרה שמתאימה ל-\( 10^{0} \). אם אנחנו רוצים חזקות קטנות יותר, אנחנו מתארים את זה במפורש על ידי כך שאנחנו שמים נקודה עשרונית בתוך המספר, ועכשיו הכלל הוא שכל מה שמשמאל לנקודה העשרונית הוא חזקות אי-שלילות של 10, וכל מה שמימין לה הוא חזקות שליליות. כך למשל \( 1.25 \) הוא סימון מקוצר לסכום \( 1\cdot10^{0}+2\cdot10^{-1}+5\cdot10^{-2} \). אם נחשב את הסכום הזה במדויק נקבל \( 1+\frac{2}{10}+\frac{5}{100}=1+\frac{1}{5}+\frac{1}{20}=\frac{20+4+1}{20}=\frac{25}{20}=\frac{5}{4}=1\frac{1}{4} \) - “אחד ורבע”.

לדעתי סיבה עיקרית לכך שהסימון הזה מבלבל (או לכל הפחות, בלבל אותי) היא שהקשר בין הספרות העשרונית לבין המספר המתואר הוא לא לגמרי ברור. \( 0.5 \) הוא חצי, אבל כשאני שומע “חצי” אני חושב על 2, כי זה 1 חלקי 2; מה קשור ה-5 הזה? ובכן, ה-5 קשור כי \( \frac{5}{10} \) זו דרך אחרת לכתוב \( \frac{1}{2} \) אבל ה-10 שנמצא במכנה פה לא נאמר במפורש ולכן מגיע הבלבול. אם לחדד: כשאני מדבר על “רבע” או “חמישית” וכדומה, אני בעצם מדבר על המכנה של המספר; אבל בייצוג עשרוני המכנה של המספר הוא תמיד חזקה של 10 והאקשן קורה בתוך המונה.

ואם חשבתם שזה מסובך, מגיע שליש ועושה לנו את החיים משוגעים לגמרי. אתם מבינים, הייצוג העשרוני של שליש הוא \( 0.333\dots \). לא, לא \( 0.333 \) שהוא פשוט דרך אחרת לרשום \( \frac{333}{1000} \), אלא \( 0.333\dots \) עם שלוש נקודות, כאשר לשלוש הנקודות כאן יש משמעות: הן אומרות לנו “הספרה 3 בעצם נמשכת עוד ועוד לנצח”. הייצוג של המספר הזה הוא אינסופי. זה אומר שכאשר כותבים את הסכום שהסימון \( 0.333\dots \) מייצג, מקבלים סכום אינסופי: \( \frac{3}{10}+\frac{3}{100}+\frac{3}{1000}+\dots \).

למתמטיקאים אין בעיות מיוחדות עם סכומים אינסופיים, בתנאי שהם מתנהגים נחמד - הולכים ומתקרבים לערך מספרי מוגדר, ובלשון מתמטית, מתכנסים. יש להתקרבות הזו הגדרה פורמלית עם מושג שנקרא גבול אבל אין שום סיבה להיכנס לזה כרגע; אפשר להוכיח שהסכום האינסופי שמוגדר על ידי ייצוג עשרוני אינסופי הוא תמיד מתכנס. מה שיעניין אותנו הוא לא להוכיח שמשהו הוא מתכנס, אלא להיות מסוגלים לחשב אותו. באופן כללי חישוב כזה עשוי להיות בעייתי, אבל במקרה שבו הייצוג העשרוני הוא מחזורי זה אפשרי, ואפשר להגיע בסופו של החישוב לשבר מהצורה \( \frac{a}{b} \) כאשר \( a,b \) שניהם מספרים שלמים.

איך מוצאים שבר מתוך הייצוג העשרוני שלו?

הכלי העיקרי שנשתמש בו בחישובים שלנו הוא הידע שלנו על איך נראה סכום טור הנדסי. טור הנדסי הוא סכום של מספרים שכל אחד מהם מתקבל מקודמו על ידי הכפלה במספר קבוע כלשהו. למשל \( 1+2+4+8+16 \) הוא סכום של חמישה איברים שכל אחד מהם התקבל מקודמו על ידי כפל ב-2. באופן כללי מסמנים זאת כך: \( 1+x+x^{2}+x^{4}+\dots+x^{n} \). יש לנו נוסחה פשוטה לסכום הזה, שמתקבלת על ידי התעלול הבא: בואו נכפול את כל הסכום ב-\( \left(x-1\right) \). מה שנקבל הוא שני עותקים של הסכום הזה, אחד עם סימנים חיוביים והשני עם סימנים שליליים, וכמעט הכל יבטל זה את זה:

\( \left(1+x+\dots+x^{n}\right)\left(x-1\right)=\left(x+x^{2}+\dots+x^{n}+x^{n+1}\right)-\left(1+x+\dots+x^{n}\right)=x^{n+1}-1 \)

עכשיו נחלק את שני האגפים ב-\( x-1 \) ונקבל:

\( 1+x+\dots+x^{n}=\frac{x^{n+1}-1}{x-1} \)

אם הסכום שלנו מתחיל במספר שונה מ-1, נאמר \( a \), אז פשוט נכפול את שני האגפים ב-\( a \) ונקבל את הנוסחה הכללית:

\( a+ax+ax^{2}+\dots+ax^{n}=a\frac{x^{n+1}-1}{x-1} \)

מהנוסחה הזו אפשר לקבל את הנוסחה גם עבור המקרה של טור הנדסי אינסופי. אני לא אכנס להוכחות, אבל הנה הרעיון: ניקח את הטור \( 1+x+x^{2}+x^{3}+\dots \) ו”נעצור” אותו אחרי \( n \) איברים. נקבל סכום ששווה ל-\( \frac{x^{n+1}-1}{x-1} \). ככל שנגדיל את \( n \) כך נתקרב יותר במדויק לסכום הטור ה”אמיתי”. בביטוי \( \frac{x^{n+1}-1}{x-1} \) ה-\( n \) מופיע רק במקום אחד: החזקה של ה-\( x^{n+1} \). שאר הסכום לא תלוי ב-\( n \). כאשר \( n \) הולך וגדל, \( x^{n+1} \) יכול להתנהג בשלוש דרכים שונות. אם \( \left|x\right|>1 \) אז \( x^{n+1} \) יילך ויגדל בערכו המוחלט, והטור לא יתכנס בכלל. אם \( \left|x\right|=1 \) אז… זה מסובך, עזבו. בואו נגיד שגם במקרה הזה הטור לא מתכנס. אם לעומת זאת \( \left|x\right|<1 \) אז \( x^{n+1} \) יילך ויקטן בערכו המוחלט ויהפוך לזניח יותר ויותר, וניתן להוכיח כי המשמעות של זה היא שאפשר להציב 0 במקום \( x^{n+1} \) בנוסחה ולקבל את סכום הטור ההנדסי האינסופי: \( \frac{0-1}{x-1}=\frac{1}{1-x} \). אם אנחנו רוצים לחשב את הסכום \( x+x^{2}+x^{3}+\dots \) שבו אין 1 בהתחלה, פשוט נחסר 1 ונקבל \( 1-\frac{1}{1-x}=\frac{x}{1-x} \).

אותנו הסכום הזה מעניין עבור \( x=\frac{1}{10} \). במקרה הזה, \( \frac{x}{1-x}=\frac{\frac{1}{10}}{\frac{9}{10}}=\frac{1}{9} \). בואו נראה איך אפשר לחשב את \( 0.333\dots \) בעזרת זה: \( 0.333\dots=\frac{3}{10}+\frac{3}{10^{2}}+\frac{3}{10^{3}}+\dots=3\left(\frac{1}{10}+\frac{1}{100}+\dots\right)=3\cdot\frac{1}{9}=\frac{1}{3} \). באופן דומה, \( 0.999\dots=9\cdot\frac{1}{9}=1 \) (יש לי פוסט שלם בנושא הטעון והרגיש הזה). אבל מה עושים עם מספר כמו \( 0.0333\dots \) שבו החלק המחזורי מתחיל רק מהספרה השניה? שום דבר מסובך - כדי לחשב את השבר של החלק המחזורי, פשוט מתחילים את הטור מ-\( \frac{1}{100} \) במקום מ-\( \frac{1}{10} \), מה שאומר לכפול את הטור ב-\( \frac{1}{10} \) ולכן גם את הסכום, שיוצא \( \frac{1}{90} \). לכן נקבל ש-\( 0.0333\dots=\frac{3}{90}=\frac{1}{30} \).

ומה עושים עם מספר שהוא מחזורי, אבל המחזוריות כוללת יותר מספרה אחת? למשל, \( 0.121212\dots \)? במקרה הזה נוח לחשוב על הטור כמורכב מחזקות של 100 ולא של 10:

\( \frac{1}{10}+\frac{2}{100}+\frac{1}{1000}+\frac{2}{10000}+\dots=\frac{12}{100}+\frac{12}{10000}+\dots=\frac{12}{99} \)

מכאן אני חושב שכבר רואים מה קורה באופן כללי: אם יש לנו מספר שמורכב מ-\( n \) ספרות שחוזרות על עצמן מייד אחרי הנקודה העשרונית, כלומר \( 0.a_{1}a_{2}\dots a_{n}a_{1}a_{2}\dots a_{n}\dots \), אז המספר הזה יהיה שווה ל-\( \frac{a_{1}\dots a_{n}}{10^{n}-1} \), כאשר מה שכתוב פה במונה למעלה הוא המספר שמתקבל מהספרות שחוזרות על עצמן, ולמטה יש לנו את \( 10^{n}-1 \) שזו דרך אחרת לומר “לכתוב \( n \) פעמים 9”.

איך זה מתקשר לשאלות שלנו?

הנה, קיבלנו תשובה לאחת מהשאלות שלנו! לכל סדרה סופית של ספרות, אנחנו יודעים למצוא מספר רציונלי שהפיתוח העשרוני שלו כולל בדיוק את החזרה על הסדרה הסופית הזו של הספרות. למשל, עבור הסדרה \( 123456789 \), זה פשוט יהיה המספר \( \frac{123456789}{999999999} \). המספר שבמונה מתחלק ב-9 כך שאפשר לכתוב את השבר הזה גם בתור \( \frac{13717421}{11111111} \), אבל זהו. יותר פשוט זה כבר לא יהיה - אין מספר טבעי שמחלק גם את המונה וגם את המכנה - זו הצגה של המספר הזה בתור שבר מצומצם.

זה מחדד את מה שאנחנו בעצם מנסים לעשות פה. אנחנו לא שואלים אילו סדרות אפשר לקבל בתור הפיתוח העשרוני של מספר רציונלי \( \frac{a}{b} \) כלשהו כי זה קל מדי. אנחנו מתעניינים בשאלה אילו סדרות אפשר לקבל שעבורן המונה יהיה 1, כלומר השבר שנותן אותן יהיה מהצורה \( \frac{1}{b} \). אפשר להוכיח יחסית בקלות ששני שברים שונים מניבים ייצוגים עשרוניים שונים, ולכן העובדה שמצאנו את הייצוג בתור שבר של \( 0.0123456789\dots \) והוא לא היה מהצורה \( \frac{1}{b} \) אומרת שפשוט לא הולך להיות לסדרה הזו ייצוג בתור שבר שכזה. זה הסבר ראשון לכך שאנחנו מתעניינים ב-\( 0.012345679\dots \) נטול ה-8, שנראה לכאורה פחות יפה - הוא אמנם לכאורה פחות יפה, אבל לפחות אותו כן אפשר לקבל בתור \( \frac{1}{b} \) (במקרה הזה, \( b=81 \)).

הסיבה שבגללה \( 0.012345679\dots \) “עובד” היא ש-\( 12345679\cdot81=999999999 \), כלומר \( \frac{12345679}{999999999}=\frac{1}{81} \). זה גם הקריטריון הכללי: כדי לקבל ייצוג בתור \( \frac{1}{b} \) לסדרה \( a_{1}\dots a_{n} \), צריך שהמספר \( a_{1}\dots a_{n} \) יחלק את \( 10^{n}-1 \), ואז ה-\( b \) שאנחנו מחפשים הוא \( \frac{10^{n}-1}{a_{1}\dots a_{n}} \).

אני מניח שגם ברור כעת שזה יעבוד באותה מידה בכל בסיס ספירה, אבל עם מספרים שונים - במקום \( 10^{n}-1 \) יהיה לנו \( d^{n}-1 \) כאשר \( d \) הוא מספר הספרות של בסיס הספירה. לכן אפשר להגיד שסיימנו עם השאלה הכללית. עדיין נשארו לנו שתי שאלות שנראות לי מהותיות: ראשית, מה הקטע עם ה-8 החסר הזה? ושנית, איך היינו יכולים לגלות שהסדרה \( 0.012345679\dots \) נוצרת על ידי חלוקה ב-81 דווקא, ועבור הסדרה של השלשות, איך היינו אמורים לגלות שהיא נוצרת על ידי \( 998001 \) דווקא?

התשובה לשאלה השניה היא לכאורה “מה הבעיה, פשוט תחלקו את \( 9999999999 \) ב-\( 12345679 \) ותקבלו 81”, אבל בפועל זה לא יעבוד עבור סדרת השלשות, למשל, כי המספר שבו אנחנו צריכים לחלק הוא עצום. יהיו בו אלפי ספרות. החלוקה הזו היא גועל נפש. היא ניתנת לביצוע בידי מחשב, כמובן, אבל איפה היופי המתמטי כאן? איך בדיוק זה עוזר לנו להבין למה דווקא 81 או למה דווקא \( 998001 \)? למרבה המזל, יש לעניין הזה פתרון אלגנטי בהרבה שאני רוצה להציג עכשיו.

ובחזרה לבעיה המקורית...

בואו נכניס לתמונה סימון מקוצר של המתמטיקאים לסכום: במקום לכתוב, למשל, \( 1+x+x^{2}+x^{3}+\dots \), הם כותבים \( \sum_{n=0}^{\infty}x^{n} \). ה-\( \Sigma \) אומר שיש פה סכום. יש לנו “אינדקס” שקוראים לו \( n \) שמקבל את הערכים הטבעיים מ-0 עד אינסוף, ולכל ערך כזה של \( n \), אנחנו מוסיפים לסכום את \( x^{n} \). הנוסחה שכבר ראינו עבור טור הנדסי היא \( \sum_{n=0}^{\infty}x^{n}=\frac{1}{1-x} \). עכשיו בואו נראה נוסחה אחרת: \( \sum_{n=1}^{\infty}nx^{n-1}=\frac{1}{\left(1-x\right)^{2}} \).

איך מוכיחים את הנוסחה הזו? אין לי הוכחה נחמדה מהשרוול כמו עבור טור הנדסי. כן יש לי הוכחה פשוטה למי שמכיר חשבון דיפרנציאלי ואינטגרלי וספציפית את התורה של טורי חזקות; אפשר לבצע לטור \( \sum_{n=1}^{\infty}nx^{n-1} \) אינטגרציה איבר-איבר ומקבלים את \( \sum_{n=0}^{\infty}x^{n} \), ולכן יש לנו את השוויון:

\( \sum_{n=1}^{\infty}nx^{n-1}=\left(\sum_{n=0}^{\infty}x^{n}\right)^{\prime}=\left(\frac{1}{1-x}\right)^{\prime}=\frac{1}{\left(1-x\right)^{2}} \)

עכשיו, אם אני מציב \( x=\frac{1}{10} \) אני אקבל באגף ימין \( \frac{10^{2}}{9^{2}} \). בואו נחלק את שני האגפים ב-\( 10^{2} \) ונקבל באגף ימין \( \frac{1}{81} \). ומה אני מקבל באגף שמאל? את הסכום הבא:

\( 0\cdot10^{-1}+1\cdot10^{-2}+2\cdot10^{-3}+3\cdot10^{-4}+4\cdot10^{-5}+\dots \)

הסכום הזה נראה כמו ההתחלה של המספר \( 0.01234\dots \). אם כן, מה משתבש? מדוע 8 הולך לאיבוד?

העניין הוא שאני מרמה ומפסיק את כתיבת הטור חיש קל. אם אני אלך עוד כמה איברים קדימה, תראו לאן אני אגיע:

\( \dots+9\cdot10^{-10}+10\cdot10^{-11}+11\cdot10^{-12}+\dots \)

כלומר, אני מגיע למקדמים שהם גדולים יותר מ-9. זה כבר לא תואם את הייצוג העשרוני של מספר, שם הספרה הגדולה ביותר היא 9. המשמעות היא שמשהו מהמקדמים הללו “זולג אחורה” לספרות הקודמות של המספר.

אני מצייר כאן את המספרים שבסכום, בשתי שורות: בשורה העליונה זו ספרת העשרות של המספרים שבסכום, ובשורה התחתונה זו ספרת האחדות שלהם. המספרים מוזחים בצורה כזו שספרת העשרות של אחד מהמספרים בסכום נמצאת מעל ספרת האחדות של המספר שבא לפניו בסכום - אני משתמש בצבעים כדי להצביע על ספרות ששייכות לאותו המספר. למשל, ה-\( 12\cdot10^{-13} \) שבסכום שלנו הוא בצבע אדום ומתואר על ידי 1 אדום בשורה העליונה ו-2 אדום בשורה התחתונה מימין לו.

כדי לדעת איזה ייצוג עשרוני נקבל בסופו של דבר, מה שצריך לעשות הוא לחבר את שתי השורות. אנחנו רואים את ה-1 הירוק שמעל ה-9 הכחול: כשנחבר אותם נקבל 0 ונשא של 1. כשנחבר את ה-1 הזה ל-8 האדום שמשמאל ל-9 הכחול, ה-8 יהפוך ל-9. זה כל הסיפור. כשאנחנו רואים \( 0.0123456790\dots \), ה-9 שאנחנו רואים הוא בעצם ה-8 שחיברו לו עוד משהו, וה-0 שאנחנו רואים הוא 9 שחיברו לו עוד משהו, וכן הלאה. זו הסיבה להיעלמות של ה-8.

עכשיו אפשר להגיע סוף סוף אל \( 998001 \), אבל אני מקווה שבשלב הזה כבר אין בעצם שאלה. \( 998001=999^{2} \), ולכן \( \frac{1}{998001} \) זה מה שנקבל מהטור \( \sum_{n=1}^{\infty}nx^{n-1}=\frac{1}{\left(1-x\right)^{2}} \) אם נציב \( x=\frac{1}{1000} \) ונחלק ב-\( 1000^{2} \). האיברים הראשונים של הסכום הזה נראים כך:

\( 0\cdot1000^{-1}+1\cdot1000^{-2}+2\cdot1000^{-3}+\dots \)

כל חזקה כזו של 1000 בעצם מכסה 3 ספרות עשרוניות, כך שאנחנו מקבלים את \( 0.000001002\dots \), והסיבה לכך ש-998 חסר היא שוב, חיבור של 1 ל-999 שהופך אותו ל-1000 והעברת ה-1 הזה אל ה-998 שהופך ל-999. זה הסיפור כולו.

אני חושב שכל העסק נחמד מאוד, אבל אני גם קצת מצטער - כשרק התחלתי לכתוב את הפוסט הזה חשבתי שיהיה לי תירוץ נחמד להציג חילוק ארוך ואיך זה עובד ובסוף הגעתי למסקנה שזה לא מועיל בשום דבר לפוסט. אצטרך לכתוב על כך פוסט נפרד! אוי לא!