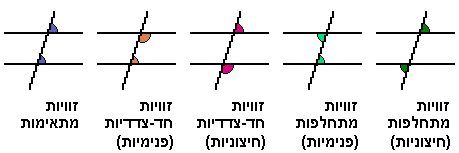בשנים האחרונות יש עיסוק הולך וגובר בבגרות במתמטיקה. טוב, על מי אני עובד, תמיד התעסקו בה. אבל בשנים האחרונות עניין 5 יחידות עלה לכותרות שוב ושוב. זה מעורר בי את התהיה - האם אני יודע לפתור את הבגרות במתמטיקה בימינו?
את הבגרות שלי עשיתי אי-שם בשנת 2000, לפני שהתחלתי ללמוד מתמטיקה ברמה אוניברסיטאית. התחושה שלי היא שמאז לא נגעתי ברוב הדברים שעליהם נבחנתי בבגרות, או שהסתכלתי עליהם בצורה כללית הרבה יותר. האם הידע הנוסף הזה עוזר לי, או מקשה עלי? האם איבדתי את היכולת הטכנית הנדרשת, או שהאתגר הטכני הוא שטויות ואני מסוגל להתגבר עליו בקלות? אני מודה שאין לי מושג. אז החלטתי לשחק משחק, לפתור בגרות בצורה מלאה ולהעלות פוסט. זה לא ניסוי מדעי ואני לא חושב שיש מסקנות שאפשר להסיק ממנו, אבל אתם מוזמנים להסיק מה שבא לכם. אל תהססו גם להעיר על טעויות (שאני בטוח שיהיו) ועל דרכים יותר טובות לפתור שאלות (שאני בטוח שיהיו) - אם אני פותר את הכל בצורה מושלמת, זה לא ממש מעניין. אני כן מקווה שאתאר מספיק לא רק את הפתרון אלא גם את אופן המחשבה שלי כדי שפוסט כמו זה יוכל לסייע לתלמידים שמתכוננים לבגרות.
בחרתי לפתור את שאלונים 316 ו-317 של קיץ 2016. הבחירה הייתה די שרירותית; אני לא בקיא במיוחד בבגרויות של השנים האחרונות ופשוט ביקשתי מאנשים לקשר לי למשהו רלוונטי. אצרף כאן צילומי מסך של כל השאלות, כמובן. בפוסט הזה אפתור את שאלון 316 ובפוסט הבא את שאלון 317.
לטובת מי שלא לא רוצה לקרוא הכל, הנה תקציר של מה שהלך בשאלון 316: שאלות האלגברה היו לי קלות מאוד ולדעתי היו נחמדות וסבירות לגמרי הן כשאלות במבחן והן כנושא לימוד. שאלות הגאומטריה לא היו קשות עבורי, אבל כן הייתי נטול ידע מספיק עבורן והייתי חייב להשתמש בגוגל כדי להיזכר בהגדרות והמשפטים הרלוונטיים (משהו שאם הייתי לומד לבגרות אני מקווה שהייתי יודע). השאלות הללו נראו לי סבירות למדי אבל אני לא בטוח אם חומר הלימוד שלהן נחוץ. שאלות החדו"א לא היו לי קשות במיוחד אבל כן היו לי כל מני טעויות חישוב מטופשות (שהצלחתי לתקן; אני מתאר את הטעויות, איך זיהיתי אותן ואיך תיקנתי בגוף השאלות) ובאופן כללי לא ממש התלהבתי מהן או מהחומר, אבל כן התרשמתי לטובה מאחת מהשאלות שבחנה לטעמי אך ורק הבנה של החומר ולא יכולות טכניות כלשהן.
יאללה, בואו נתחיל.
שאלה 1
סעיף א
בשאלה הזו ברור מייד שהאתגר העיקרי יהיה לתרגם את השאלה המילולית למשוואות אלגבריות. בסיטואציות כאלו צריך לעבור שורה שורה בזהירות כדי לפספס משהו. בקריאה הראשונית שלי פספסתי את "ביום העבודה הראשון הרכיבו שני הטכנאים אותו מספר של מחשבים" ובהיתי בדף כשאני תוהה איפה הנתון שחסר לי.
אז בואו נלך בזהירות. יש לנו טכנאים שמרכיבים מחשבים, כלומר מבצעים המרה של זמן למחשבים. להמרה כזו יש קצב - נותנים כך-וכך דקות, מקבלים כך-וכך מחשבים. לכל טכנאי יש קצב משלו, אז בואו נסמן את הקצבים הללו באותיות: \(s_{1},s_{2}\). עכשיו, אם \(t\) היא כמות זמן כלשהי, אז \(ts_{1}\) זו כמות המחשבים שהטכנאי הראשון הרכיב בזמן הזה. בואו נסמן ב-\(T_{1},T_{2}\) את הזמן הכולל שבו שניהם עבדו באותו היום, אז מכך ש"ביום העבודה הראשון הרכיבו שני הטכנאים אותו מספר של מחשבים" קיבלנו את המשוואה הראשונה שלנו:
\(T_{1}s_{1}=T_{2}s_{2}\)
כרגע זו משוואה אחת עם ארבעה נעלמים - משהו שאנחנו לא יודעים לפתור, יש יותר מדי חופש בחירה. אז קוראים את המשך התרגיל ומחפשים עוד נתונים. מייד מקבלים אחד: "גל התחיל לעבוד בשעה 8:00 וסיים לעבוד בשעה 15:00". אם יחידות המדידה שלנו לזמן הן שעות, אז קיבלנו ש-\(T_{1}=7\). ומה עם דני? "התחיל לעבוד לאחר 8:00 ולפני 9:00 וסיים לעבוד בשעה 13:00". אז כאן יש לנו נעלם - אנחנו יודעים שזמן העבודה הכולל של דני הוא \(5-x\) כאשר \(x\) הוא הזמן אחרי 8:00 שבו הוא התחיל לעבוד - וזה בדיוק המספר שאנחנו מחפשים. אנחנו יודעים ש-\(0
\(7s_{1}=\left(5-x\right)s_{2}\)
עדיין יש לנו כאן יותר מדי נעלמים - \(s_{1},s_{2},x\). זה יותר מדי מכדי שנוכל למצוא את \(x\). לכן אנחנו מחפשים עוד נתונים בשאלה, ומקבלים: "ידוע שגל ודני הרכיבו אותו מספר של מחשבים מהרגע שכל אחד מהם התחיל לעבוד ועד השעה 9:00". גל עבד שעה אחת, בזמן שדני עבד \(1-x\) שעה בזמן הזה. קיבלנו משוואה נוספת:
\(1\cdot s_{1}=\left(1-x\right)s_{2}\).
קיבלנו ביטוי ל-\(s_{1}\). נציב אותו חזרה במשוואה הראשונה ונקבל:
\(7\left(1-x\right)s_{2}=\left(5-x\right)s_{2}\)
מה שאנחנו רוצים לעשות הוא לחלק ב-\(s_{2}\). בשביל זה צריך לוודא שהוא שונה מ-0. נשמע די אבסורדי שהוא יהיה שווה לאפס כי זה אומר שדני מייצר 0 מחשבים ולא משנה כמה זמן נותנים לו, ולכן אני מניח ש-\(s_{2}\ne0\). כאן קופץ לי המתמטיקאי: האם ייתכן ש-\(s_{1}=s_{2}=0\) בכל זאת? התשובה היא כן, ואם זה המצב, אז כל \(x\) הוא תשובה לגיטימית. אבל זו סיטואציה מנוונת ומטופשת וברור לי שלא לכך התכוונו. זו שאלה מעניינת מה עשו במבחן למי שפשוט חילק ב-\(s_{2}\) בלי להתייחס לשאלה האם הוא אפס או לא.
אחרי שנחלק ב-\(s_{2}\) נקבל את המשוואה \(7-7x=5-x\) שאותה מן הסתם טריוויאלי לפתור על ידי העברת אגפים. נקבל \(6x=2\), כלומר \(x=\frac{1}{3}\), כלומר דני התחיל לעבוד ב-8:20 (כי "שליש" פה הוא שליש שעה, 20 דקות).
סעיף ב
עכשיו יש לנו יום חדש, ולכן זמני עבודה חדשים. שימו לב שאת \(s_{1},s_{2}\) לא גילינו, אבל אנחנו לא באים לסעיף הזה בידיים ריקות - בסעיף הקודם גילינו ש-\(s_{1}=\left(1-\frac{1}{3}\right)s_{2}\) וכנראה נצטרך להשתמש בזה גם כאן.
זמני העבודה של שני המרכיבים זהים הפעם - נסמן את זמן העבודה הזה ב-\(T\). עכשיו מדברים על סך כל המחשבים ששניהם הרכיבו - זה יהיה \(Ts_{1}+Ts_{2}=T\left(s_{1}+s_{2}\right)=T\left(1-\frac{1}{3}+1\right)s_{2}=\frac{5}{3}Ts_{2}\).
המטרה שלנו היא למצוא את \(T\), כשנותנים לנו נותן נוסף - שסך כל המחשבים שהורכבו ביום השני שווה לסך כל המחשבים שהורכבו ביום הראשון. כמה הורכבו ביום הראשון? מצאנו את ה-\(T_{1},T_{2}\) של היום הראשון ולכן אנחנו יודעים זאת:
\(T_{1}s_{1}+T_{2}s_{2}=7s_{1}+\left(5-\frac{1}{3}\right)s_{2}=7\left(1-\frac{1}{3}\right)s_{2}+\left(5-\frac{1}{3}\right)s_{2}=\left(7-\frac{7}{3}+5-\frac{1}{3}\right)s_{2}=\left(12-\frac{8}{3}\right)s_{2}=\frac{28}{3}s_{2}\)
נשאר רק לכתוב את השוויון:
\(\frac{5}{3}Ts_{2}=\frac{28}{3}s_{2}\)
נצמצם ב-\(s_{2}\) (שוב, אפשר להניח שהוא לא אפס), נכפול ב-\(\frac{3}{5}\) ונקבל:
\(T=\frac{28}{5}=5\frac{3}{5}\)
כלומר, הם עבדו חמש שעות ו-36 דקות ביום השני. זה נשמע יחסית סביר - הטכנאי הראשון עובד קצת פחות, השני קצת יותר. כמובן שעוד בדיקה יכולה רק להועיל כאן.
מה דעתי על השאלה?
זו נראית לי כמו שאלה סבירה לגמרי. מבחינת המטרה שלה, לדעתי אחד מהדברים החשובים ביותר במתמטיקה "יומיומית" הוא היכולת לתרגם סיטואציות מילוליות למשוואות המתמטיות הרלוונטיות ("למדל את הסיטואציה"), לדעת לזהות אם חסר נתון או לא, וכדומה. את כל זה יש כאן. המשוואות שצריך לפתור בסופו של דבר הן פשוטות ביותר (משוואות לינאריות שאפשר לפתור עם הצבה ובלי דברים מתוחכמים).
שאלה 2
סעיף א'
הסעיף הזה עוסק בסכום של סדרות חשבוניות, אז קודם כל צריך להיזכר בנוסחת הסכום. יש בדפי הנוסחאות, כמובן, אבל אני לא מסתכל בדפי הנוסחאות בלי סיבה. בואו ננסה לפתח את זה בעצמנו: התעלול הישן של גאוס למציאת סכום של סדרה חשבונית התבסס על חיבור האיבר הראשון והאחרון, ואז הצבעה על כך שהסכום הזה שווה גם לסכום של האיבר השני והלפני אחרון וכן הלאה, כך שמספיק לכפול את הסכום הזה במספר האיברים הכולל בסדרה חלקי 2 (כי כל זוג משתמש בשני איברים מהסדרה). לכן נוסחה אפשרית אחת לסכום היא זו: אם הסדרה שלנו היא \(a_{1},a_{2},\dots,a_{n}\) אז הסכום שלה הוא \(\left(a_{1}+a_{n}\right)\frac{n}{2}\). למה אני הולך דווקא על הנוסחה הזו? כי יש לי יכולת ראיית הנולד (או ליתר דיוק, כי אחרי שחשבתי קצת על התרגיל הגעתי למסקנה שזו הדרך הכי פשוטה): הסדרה החדשה שאני בונה תהיה מאוד דומה לנוכחית בפרמטרים שיש כאן. האיבר הראשון והאחרון שלה יהיו אותם איברים, וההפרש בין איברים סמוכים לא משחק תפקיד בכלל בנוסחה הזו. כל מה שחשוב הוא מספר האיברים הכולל. בסדרה החדשה הוספתי איבר חדש אחרי כל איבר קיים בסדרה המקורית, למעט האיבר האחרון. כלומר הוספתי \(n-1\) איברים חדשים וקיבלתי סדרה עם \(2n-1\) איברים בסך הכל. לכן סכום הסדרה החדשה הוא \(\left(a_{1}+a_{n}\right)\frac{2n-1}{2}\). קל לראות שהיחס בין שני הערכים הללו אכן יוצא \(\frac{2n-1}{n}\).
עכשיו מוסיפים לנו נתונים: ראשית אומרים ש-\(\frac{2n-1}{n}=\frac{19}{10}\), ולכן מיידית אני רואה ש-\(n=10\) (אפשר גם לכפול ולפתור את המשוואה). כמו כן נותנים לי את הסכום של האיברים החדשים שהוכנסו לסדרה, ומבקשים ממני למצוא את האיבר הראשון בסדרה המקורית. כאן מן סתם אצטרך להשתמש בנתון שטרם השתמשתי בו - שהפרש האיברים בסדרה המקורית הוא 3.
בואו נסמן את האיברים שהוספתי בתור \(b_{1},b_{2},\dots,b_{n-1}\). אז סכומם הוא \(\left(b_{1}+b_{n-1}\right)\frac{n-1}{2}=130\frac{1}{2}\). אני יודע מהו \(n\) אז תנו לי שניה לפשט: \(\left(b_{1}+b_{9}\right)\frac{9}{2}=130\frac{1}{2}\), כלומר \(b_{1}+b_{9}=\frac{261}{9}\). כדי למצוא מזה את \(b_{1}\) אני צריך למצוא את הפרש הסדרה של ה-\(b\)-ים. לי ברור אינטואיטיבית שהוא יהיה 3, אבל אנחנו בבגרות פה - בואו לא נשתמש באינטואיציה אלא נשכנע את עצמנו שאנחנו צודקים.
המידע הרלוונטי לנו הוא שאחרי הוספת ה-\(b\)-ים קיבלנו סדרה חשבונית חדשה. אם הסדרה המקורית התחילה ב-\(a_{1},a_{2},\dots\) כך ש-\(a_{2}-a_{1}=3\) הרי שבסדרה החדשה ההתחלה היא \(a_{1},b_{1},a_{2},\dots,\) כך ש-\(b_{1}-a_{1}=a_{2}-b_{1}\). נעביר אגפים ונקבל \(2b_{1}=a_{2}+a_{1}\). נחסר את המשוואה \(a_{2}-a_{1}=3\) מהמשוואה הזו וקיבלנו \(2b_{1}-3=2a_{1}\), כלומר \(b_{1}=a_{1}+\frac{3}{2}\). כאמור, אין כאן הפתעה גדולה, אבל זה צעד שצריך לעשות. כעת, \(b_{2}=a_{2}+\frac{3}{2}=b_{1}+\frac{3}{2}+\frac{3}{2}=b_{1}+3\) כך שקיבלנו את מה שרצינו.
עכשיו צריך לדעת מהו \(b_{9}\), אבל זה קל: \(b_{9}=b_{1}+3\left(9-1\right)=b_{1}+24\) (כי הוספנו 3 פעם אחת כדי להגיע ל-\(b_{2}\), ואז פעמיים כדי להגיע ל-\(b_{3}\) וכן הלאה). קיבלנו \(2b_{1}+24=\frac{261}{9}\), ולכן \(2a_{1}+3+24=\frac{261}{9}\), ולכן \(a_{1}=\frac{261}{18}-\frac{27}{2}=\frac{261-243}{18}=\frac{18}{18}=1\). כן, השתמשתי במחשבון בשביל החישוב הזה, ואני לא מתבייש בכך!
סעיף ב'
כאן אנחנו רואים שהמשחק ששיחקנו קודם כדי למצוא את ההפרש \(\frac{3}{2}\) לא היה מיותר לגמרי - מבקשים מאיתנו לעשות את אותו הדבר רק עם הוספה של \(k\) איברים. מה הסיטואציה כאן? אנחנו מקבלים \(a_{1},b_{1},b_{2},\dots,b_{k},a_{2},\dots\) בתחילת הסדרה, כך ש-\(a_{2}-a_{1}=3\) ואני יכול לחלץ גם את המשוואה \(b_{1}-a_{1}=a_{2}-b_{k}\) שממנה מתקבל \(b_{1}+b_{k}=a_{1}+a_{2}\). זה דומה למה שהיה קודם, רק שאז התקיים \(b_{k}=b_{1}\) וזה פישט את הסיטואציה. מכל מקום שוב אפשר לחסר את המשוואה הראשונה מהשניה ולקבל \(b_{1}+b_{k}-k=2a_{1}\). כדי להמשיך לפשט את זה, יהיה נוח לתאר את \(b_{k}\) באמצעות \(b_{1}\). נסמן את הפרש הסדרה שאנחנו מחפשים ב-\(d\), אז \(b_{k}=b_{1}+\left(k-1\right)d\). קיבלנו ש-\(2b_{1}+\left(k-1\right)d=2a_{1}+3\). נחלק ב-2, נעביר את \(a_{1}\) אגף, נשתמש בכך ש-\(b_{1}-a_{1}=d\), ונקבל \(d+\frac{k-1}{2}d=\frac{3}{2}\). כלומר \(d\left(1+\frac{k-1}{2}\right)=\frac{3}{2}\), כלומר \(d\left(\frac{k+1}{2}\right)=\frac{k}{2}\), כלומר \(d=\frac{3}{k+1}\). הנה בדיקת שפיות זריזה: כאשר \(k=1\) (המקרה שממנו התחלנו) אני מקבל \(d=\frac{3}{2}\), כמו שקיבלתי קודם. אם \(k=2\) אני מקבל \(d=\frac{3}{3}=1\) וזה הגיוני (חשבו על הסדרה \(0,3,6,\dots\) שהופכת פתאום ל-\(0,1,2,3,\dots\)).
מה דעתי על השאלה?
גם זו נראית לי כמו שאלה טובה אם אנחנו רוצים לבדוק יכולות אלגבריות בסיסיות. סדרות חשבוניות הם יצורים מתמטיים טובים ללימוד בתיכון - מצד אחד, הם לא חסרי כל קשר למציאות (כן אפשר להתקל פה ושם בסדרות חשבוניות בפועל) ומצד שני, הם פשוטים מאוד - אפשר להבין אותם לא רע עד הסוף (למשל, קל למצוא את נוסחת הסכום או את הנוסחה לאיבר כללי). השאלה הזו דורשת חשיבה ולא סתם הצבה בנוסחאות - צריך להבין מה בדיוק משתנה כשמשנים את הסדרה, ומה לא; העובדה שבחרתי לפתור את הסעיף הראשון בעזרת נוסחת הסכום שמבוססת על סכום האיבר הראשון והאחרון פישטה לי מאוד את העבודה - עם נוסחה אחרת הייתי ממש מסתבך ואולי לא מצליח להוכיח בכלל. השאלות פה הן גם יחסית אבסטרקטיות - הראשונה ממש מבקשת להוכיח שמשהו מתקיים, והשניה מבקשת פתרון שתלוי בפרמטר. לא רע.
שאלה 3
סעיף א'
נתחיל קודם כל מלתת שמות לדברים. ההסתברות שיעל תנצח היא \(p\), ההסתברות שאנה תנצח היא \(q\), ולכן ההסתברות לתיקו ביניהן היא \(1-\left(p+q\right)\). בסעיף הזה אנחנו מתבקשים למצוא את \(p\). הנתון שיש לנו נוגע להסתברות של יעל לנצח ב-2 או 3 משחקים, ובהסתברות שלה לנצח ב-4 משחקים. איזו סוג של התפלגות יש לנו פה? אני לא יודע איך קוראים לזה בתיכון או אילו משוואות נותנים, אבל זו התפלגות בינומית: אם יש לנו \(n\) משחקים עם הסתברות \(p\) לנצח בכל משחק, אז ההסתברות לנצח בדיוק ב-\(k\) משחקים היא \({n \choose k}p^{k}\left(1-p\right)^{n-k}\) (לכל בחירה של \(k\) מתוך \(n\) משחקים אנחנו סופרים את האפשרות שיעל תנצח בדיוק במשחקים הללו; לשם כך עליה לנצח בדיוק בהם - זה \(k\) פעמים ההסתברות \(p\) - ולהפסיד בכל היתר - זה \(n-k\) פעמים ההסתברות \(1-p\)).
ההסתברות לנצח ב-4 משחקים היא הקלה ביותר כאן - זו בדיוק \(p^{4}\). ההסתברות לנצח בשניים או שלושה משחקים היא
\({4 \choose 2}p^{2}\left(1-p\right)^{2}+{4 \choose 3}p^{3}\left(1-p\right)\)
\(=6p^{2}\left(1-p\right)^{2}+4p^{3}\left(1-p\right)\)
\(=p^{2}\left(1-p\right)\left(6\left(1-p\right)+4p\right)\)
\(=p^{2}\left(1-p\right)\left(6-2p\right)\)
על פי הנתון של "גדולה פי 10" קיבלנו כעת את המשוואה:
\(p^{2}\left(1-p\right)\left(6-2p\right)=10p^{4}\)
פתרון אחד של המשוואה הזו הוא \(p=0\). אולי לזה התכוונו? הם לא פסלו את האפשרות שיעל פשוט לא יכולה לנצח אף פעם. בינתיים אניח שלא התכוונו לזה, כלומר ש-\(p\ne0\) ואפשר לחלק בו, ונראה אם יצוץ עוד פתרון. נחלק ב-\(2p^{2}\) ונקבל:
\(\left(1-p\right)\left(3-p\right)=5p^{2}\)
וזו משוואה ממעלה שניה, כלומר משהו שאנחנו יודעים לפתור איכשהו. אני לא רואה פה טריק כלשהו פרט לפתיחת סוגריים, כינוס איברים ופתרון בעזרת הנוסחה הכללית:
\(5p^{2}=3-4p+p^{2}\)
\(4p^{2}+4p-3=0\)
\(p_{1,2}=\frac{-4\pm\sqrt{16+48}}{8}=\frac{-4\pm\sqrt{64}}{8}=\frac{-4\pm8}{8}=-\frac{1}{2}\pm1\)
כלומר קיבלנו שני פתרונות: האחד הוא \(-\frac{3}{2}\) שהוא שלילי ולכן לא רלוונטי כי הסתברות לא יכולה להיות שלילית; והשני הוא \(p=\frac{1}{2}\). אני מציב אותו במשוואה כדי לוודא שאני אכן מקבל אפס (אני מקבל אפס) ולכן זהו לכאורה הפתרון. כדי להיות בטוח אני מחשב גם את ערכי ההסתברות שאיתם התחלתי. בגלל ש-\(p=\frac{1}{2}\) זה יוצא קל במיוחד, כי עכשיו \(p=\left(1-p\right)\) ולכן \(p^{4}=p^{2}\left(1-p\right)^{2}=p^{3}\left(1-p\right)\); בעצם כל מה שנותר לבדוק הוא ש-\({4 \choose 2}+{4 \choose 3}=10\).
סעיף ב'
עכשיו אנחנו צריכים למצוא את \(q\), ועוזרים לנו על ידי מתן מידע על תוצאות תיקו - אומרים שהסיכוי לתיקו בסבב השני כולו היא \(0.34\). איך תיקו כזה יכול להיווצר? יש שתי דרכים שונות: או שיעל תנצח במשחק אחד ואנה תנצח בשני, או שהן יוציאו תיקו בשני המשחקים. הסיטואציה הראשונה היא בעצם שתי סיטואציות - באחת מהן יעל מנצחת קודם ובשניה אנה מנצחת קודם. אני אכתוב את סכום ההסתברויות של כל שלושת התרחישים הללו:
\(p\cdot q+q\cdot p+\left(1-\left(p+q\right)\right)^{2}=\frac{34}{100}\)
כמובן, יש לנו את הסעיף הראשון לעזור לנו - אנחנו כבר יודעים ש-\(p=\frac{1}{2}\). אז בעצם קיבלנו פה משוואה בנעלם יחיד:
\(\frac{1}{2}q+\frac{1}{2}q+\left(\frac{1}{2}-q\right)^{2}=\frac{34}{100}\)
ושוב, אני לא רואה משהו חכם לעשות כאן מלבד לפתוח סוגריים, להעביר אגפים ולהשתמש בנוסחה הכללית:
\(q+\frac{1}{4}-q+q^{2}=\frac{34}{100}\)
רגע, רגע, רגע! רואים? יש טוויסט בעלילה, ה-\(q\) שאינו בריבוע מצטמצם! אנחנו מקבלים \(q^{2}=\frac{34}{100}-\frac{25}{100}=\frac{9}{100}\) ומכאן מייד \(q=\frac{3}{10}\) (שוב, אני מתעלם מהפתרון השלילי) בלי שאצטרך להשתמש בנוסחת השורשים הכללית.
כמו קודם, בדיקת שפיות היא תמיד מועילה - אני מציב את \(q\) בנוסחה שקיבלתי בהתחלה ומחשב: \(\frac{3}{20}+\frac{3}{20}+\left(1-\frac{8}{10}\right)^{2}=\frac{6}{20}+\frac{4}{100}=\frac{34}{100}\) - יופי, אני מרוצה.
סעיף ג'
כאן יש לנו שאלה בהסתברות מותנה. אני צריך לחשב את ההסתברות של התרחיש "אנה מנצחת במשחק השני וגם יש בסך הכל שוויון" ולחלק בהסתברות של התרחיש "בסך הכל יש שוויון". את ההסתברות הזו אני כבר יודע - היא \(\frac{34}{100}\). מה ההסתברות שאנה תנצח במשחק השני וגם יהיה שוויון? אין כאן משהו מחוכם - אם אנה מנצחת במשחק השני ויש שוויון, יעל חייבת לנצח במשחק הראשון, כלומר הסתברות של \(pq=\frac{3}{20}\). נחלק ונקבל \(\frac{\frac{15}{100}}{\frac{34}{100}}=\frac{15}{34}\).
מה דעתי על השאלה?
יש כאן הסתברות ברמה מאוד בסיסית, כמובן, אבל לדעת הסתברות בכל רמה שהיא זה מצוין. זה אחד מהדברים שהכי כדאי להכיר עבור מי שלא ילמד מתמטיקה באופן רציני בעתיד. החישובים עצמם הם פשוטים אבל דורשים היכרות עם הנוסחאות הבסיסיות בהסתברות ועם נוסחת השורשים, שאת כולם צריך לדעת. גם פה, אין לי תלונות בכלל. כל החלק של "אלגברה והסתברות" נראה לי הוגן לגמרי, וחשוב יחסית.
שאלה 4
אוי לי. גאומטריה. מזה פחדתי. אם יש משהו שאני בטוח שאפשל בו, זה זה. טוב, בואו נראה את השאלה...
סעיף א
כן, אין לי מושג.
ניגשתי למבחן הזה בלי ללמוד את החומר קודם; חלק עיקרי מהפואנטה היה לראות מה אני יודע מהיומיום המתמטי שלי ומה לא. בכל הנוגע לגאומטריה אוקלידית לא היו לי אשליות - אני יודע מעט מאוד. זה לאו דווקא חיובי - לדעת קצת גאומטריה אוקלידית נראה לי הכרחי למתמטיקאי-לשם-שעשוע - אבל זה תמיד היה חור שחור יחסי בשבילי, ועכשיו המצב לא שונה.
אם כן, אני יכול סתם לומר שאני לא יודע איך פותרים את השאלה. אבל קצת חבל לוותר כל כך מהר. תחת זאת אני אחפש את המשפטים הרלוונטיים ונראה אם אני מצליח להתקדם מכאן; הלקח מבחינתי הוא שלפני שאני ניגש לבגרות במתמטיקה כדאי לי לחזור על כל החומר בגאומטריה אוקלידית.
אז מה אני מגגל? ראשית כל, את "מרובע בר חסימה במעגל" - זה משהו שאני לא זוכר שלמדתי מעולם. גיגול מהיר מוצא תשובה מפורום כלשהי שאומרת "כדי שיהיה ניתן לחסום מרובע במעגל, סכום זוג אחד של זוויות נגדיות במרובע חייב להיות 180 מעלות". יופי, זה כבר מקדם אותי מאוד, לשמחתי. הדבר השני שאני צריך בסעיף הזה הוא להיזכר איך מוכיחים שישרים הם מקבילים. אני זוכר שאם ישרים הם מקבילים אז יש כל מני קסמים עם הזוויות שנשענות עליהם; אבל האם זה כך גם בכיוון ההפוך? אני די בטוח שכן, אבל למה לנחש - אני מגגל "להוכיח ישרים מקבילים" ומוצא מישהו שאומר "אם בין שני ישרים זוויות מתחלפות שוות אזי הישרים מקבילים". יופי, זה כל מה שאני צריך. זה, ולזכור מה אלו הזוויות המתחלפות. אני מגגל "מקבילים מתחלפות" ומקבל תמונה נחמדה שמזכירה לי. הנה תמונה אחרת בשבילכם שבה כבר יש יותר מידע (בשלי היה רק את המתחלפות ואני לא מוצא אותה כרגע):
כאן זה לא לגמרי מתאים לי כי אין שתי זוויות מתחלפות שאפשר לתת להן שמות מפורשים. יותר קל לי יהיה לעבוד עם הזוויות ה... איך קראו לזה? אה, כן, חד צדדיות! אני מגגל "מקבילים חד צדדיות" ומקבל לשמחתי את מה שקיוויתי לקבל - "משפט: אם עבור שני ישרים הנחתכים על-ידי ישר שלישי, מתקיים שסכום שתי זוויות חד-צדדיות הוא \(180^{\circ}\) אזי הישרים הנחתכים הם מקבילים".
יופי. בואו ניגש לעבודה. מכיוון ש-\(\text{ABLK}\) הוא בר-חסימה במעגל יש לו שתי זוויות נגדיות שסכומן הוא 180 מעלות. כמובן, אני יכול להגיד קצת יותר מזה - מכיוון שסכום הזוויות במרובע הוא \(360^{\circ}\), אם סכום זוג אחד של זוויות נגדיות הוא \(180^{\circ}\) זה גם סכום הזוג השני. את החוכמה הזו אני יכול לומר גם על המרובע \(\text{KLCD}\). אם כן, בואו נתחיל דווקא ממה שאני רוצה להוכיח - אני רוצה להוכיח ש-\(\text{AB}\) מקביל ל-\(\text{DC}\) ולצורך כך מספיק לקחת שתי זוויות חד-צדדיות ולהראות שסכומן הוא \(180^{\circ}\). בואו ננסה להראות, אם כן, כי \(\angle DAB+\angle ADC=180^{\circ}\). כעת, \(\angle DAB=\angle KAB\) ומהנתון על כך ש-\(\text{ABLK}\) חסום אני יודע ש-\(\angle KAB+\angle KLB=180^{\circ}\) ו... אה, עזבו את זה. אני כבר מבין לאן זה הולך, בואו תנו לי לרשום את זה כבר בפורמט ה"רשמי" של הוכחות גאומטריות, זה יהיה יותר קריא ככה:
- \(\angle KAB+\angle KLB=180^{\circ}\) (במרובע \(\text{ABLK}\) החסום במעגל סכום זוויות נגדיות הוא \(180^{\circ}\)).
- \(\angle KLB+\angle KLC=180^{\circ}\) (סכום זוויות צמודות הוא \(180^{\circ}\) - כן, הייתי צריך לגגל כדי לזכור שקוראים לזה "זוויות צמודות").
- \(\angle KLC+\angle KDC=180^{\circ}\) (במרובע \(\text{KLCD}\) החסום במעגל סכום זוויות נגדיות הוא \(180^{\circ}\)).
- \(\angle KAB+\angle KDC=180^{\circ}\) (חיבור 2 ו-4 והחסרת 3).
- \(\angle DAB=\angle KAB\) (איך מנמקים את זה? על פי הגדרה?)
- \(\angle ADC=\angle KDC\) (אותה שאלה כמו ב-5)
- \(\angle DAB+\angle ADC=180^{\circ}\) (הצבה של 5 ו-6 בתוך 4).
- \(AB||DC\) (אם עבור שני ישרים הנחתכים על-ידי ישר שלישי, מתקיים שסכום שתי זוויות חד-צדדיות הוא \(180^{\circ}\) אזי הישרים הנחתכים הם מקבילים).
סעיף ב'
כאן אני מקבל כמה נתונים מספריים וצריך לעשות איתם משהו. לפני שאני מתעמק בהם, בואו נבין מה צריך לעשות עכשיו. שואלים אותי אם אפשר לחסום במעגל את המרובע \(\text{ABCD}\). אז שוב מדובר על אותו קריטריון כמו קודם, רק שהפעם אני מנחש שהתשובה תהיה שלילית. אני צריך להעריך סכום של שתי זוויות נגדיות במרובע הזה, ונראה שהפעם גם המשולש \(\text{PAB}\) יהיה רלוונטי. מייד קופץ לי לעין גם איך: ניקח למשל את הזוויות הנגדיות \(\angle ADC\) ו-\(\angle ABC\). אז בגלל מה שהוכחנו בסעיף א', \(\angle ADC=\angle PAB\), ובגלל זוויות צמודות אני יודע ש-\(\angle ABC=180^{\circ}-\angle PBA\). אם כן, אם מתקיים \(\angle ADC+\angle ABC=180^{\circ}\) נובע מכך ש-\(\angle ADC=\angle PBA\), כלומר \(\angle PAB=\angle PBA\), כלומר המשולש \(PAB\) הוא שווה שוקיים. אבל הוא לא שווה שוקיים כי \(PA\ne PB\), וזה מסיים את זה. הפעם אין לי כוח אפילו לכתוב פתרון פורמלי.
סעיף ג'
כאן מה שקופץ לי לראש מייד הוא "דמיון משולשים". המשולש \(PAB\) בבירור דומה למשולש \(PDC\) כי הזווית \(\angle APB\) משותפת לשניהם והזוויות האחרות שוות בגלל הקטע הזה עם המקבילים. יש לי מידע על אורך \(PA\) אז אני אוכל להפיק מידע על אורך \(PD\) אם רק יהיה לי מידע על הפרופורציה הכוללת בין המשולשים. האם יש לי משהו? ובכן, כן: השטח של \(PDC\) הוא סכום השטחים של \(PAB\) ושל \(ABCD\), כלומר הוא \(25S\). עכשיו, מה היחס בין השטחים של משולשים דומים, בהינתן היחס בין הצלעות? אני לא זוכר, אבל מנחש שריבוע. אבל למה לנחש, בואו נפתח את זה מחדש: אם \(ABC\) דומה למשולש \(abc\) עם יחס קבוע \(\frac{A}{a}=\frac{B}{b}=\frac{C}{c}=x\), אז אותו דבר יתקבל גם עם גבהים שנסמן בתור \(H\) ו-\(h\) מאחד הקודקודים לאחת הצלעות, נאמר ל-\(A\) ו-\(a\). כלומר, \(\frac{H}{h}=x\) גם כן. כעת, השטח של המשולשים הוא \(S=\frac{AH}{2}\) ו-\(s=\frac{ah}{2}\). לכן המנה תהיה \(\frac{S}{s}=\frac{AH}{ah}=x^{2}\) - הא, צדקתי! כעת, היחס בין שטח \(PDC\) ובין שטח \(PAB\) הוא \(25\), ולכן קבוע יחס הדמיון של המשולשים הוא 5, ולכן אורך \(PD\) הוא פי 5 מאורך \(PA\), כלומר \(PD=15\).
סעיף ד'
כאן אני צריך למצוא את שטח \(KLCD\), מה שמזכיר לי בעיה קטנה - אין לי מושג איך מחשבים שטח של מרובע כללי. אבל אחרי כמה רגעים של מחשבה אני רואה שבכלל לא צריך את זה. זה מסך עשן. אני יודע ששטח המשולש הכולל הוא \(25S\); אם אצליח למצוא את שטח המשולש \(PKL\) ואחסר את זה מ-\(25S\) אקבל את המספר שאני צריך. אז השאלה היא בעצם מה שטח \(PKL\). איך עושים את זה?
לא אלאה אתכם בכיוונים השונים והמשונים שחשבתי עליהם כאן. בהתחלה הייתי בטוח שיש כאן משפט הקוסינוסים ומשפט הסינוסים ומה לא. בסוף, כשהתחלתי לנסות להשתמש בהם, ראיתי שכל זה היה מיותר לגמרי. האבחנה שמפילה את האסימון היא שהמשולש \(PKL\) דומה למשולש \(PAB\), למרות שבתמונה זה לא נראה כך בכלל; הוא פשוט דומה לו עם היפוך הצלעות. יש לנו את זווית הראש \(\angle KPL\) שהיא משותפת, וקל לראות שגם \(\angle AKL=\angle ABP\), משיקולים דומים לאלו של סעיף א'. עכשיו היתר מגיע מאליו: אורך הצלע \(PA\) הוא 3 על פי הנתון. אורך הצלע \(PL\) הוא \(PB+BL\) כאשר \(BL\) הוא הנתון החדש שלנו. כלומר, אורך \(PL\) הוא 9. מכאן שקבוע הפרופורציה בין המשולשים הוא 3, ולכן קבוע הפרופורציה בין השטחים שלהם הוא 9, ולכן שטח \(PKL\) הוא \(9S\) ולכן שטח \(KLCD=25S-9S=16S\). קל מאוד, כשמבינים מה לעשות!
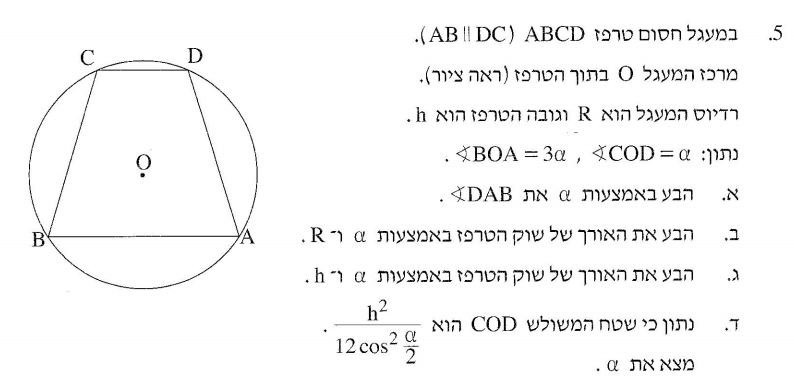
שאלה 5
סעיף א'
הדבר הראשון שקופץ לי לראש הוא השאלה הקודמת: אם הטרפז חסום במעגל, אז זוויות נגדיות משלימות ל-\(180^{\circ}\). ביחד עם זה ש-\(AB\) מקביל ל-\(CD\) אני מקבל שגם זוויות סמוכות משלימות ל-\(180^{\circ}\), ומכאן שהטרפז הוא שווה שוקיים. וזה עוזר לי... אין לי מושג איך.
אז הנה גישה אחרת: בואו נחבר את כל הקודקודים עם מרכז המעגל \(O\). מקבלים ככה ארבעה משולשים שווי שוקיים. אם אנחנו מחפשים את \(\angle DAB\) אז מספיק לנו למצוא את \(\angle DAO\) ואת \(\angle OAB\) ולחבר, וכל זווית כזו היא זווית בסיס באחד מהמשולשים שווי השוקיים. בפרט \(\angle OAB\) היא זווית בסיס במשולש שזווית הראש שלו היא \(3\alpha\), ולכן \(\angle OAB=90^{\circ}-\frac{3}{2}\alpha\).
מה עם \(\angle DAO\)? היא זווית בסיס במשולש שאין לנו במפורש את זווית הראש שלו, אבל מכך שסכום כל הזוויות של ארבעת המשולשים שנשענים על \(O\) צריך להיות \(360^{\circ}\) ומכך שהטרפז שווה שוקיים אני יכול להסיק ש-\(\angle DOA=\angle COB\) ו-\(\angle DOA+\angle COB=360^{\circ}-4\alpha\), כלומר \(\angle DOA=180^{\circ}-2\alpha\). על כן, \(\angle DAO=90^{\circ}-\frac{\left(180^{\circ}-2\alpha\right)}{2}=\alpha\). מכאן קיבלנו ש-\(\angle DAB=90^{\circ}-\frac{3}{2}\alpha+\alpha=90^{\circ}-\frac{\alpha}{2}\). תסלחו לי אם לא אכתוב פתרון פורמלי.
סעיף ב'
אוקיי. זה מביך. נתקעתי על הסעיף הזה כמות לא הגיונית בעליל של זמן, נטשתי אותו, חזרתי אליו ביום אחר, ופתרתי אותו מייד. אני מאשים את עצמי. בפרט את החשיבה האוטומטית שלי. בפרט את זה שבכלל לא טרחתי לצייר את הסיטואציה בעצמי ולהעביר קווים וכאלה.
כשראיתי את השאלה הדבר הראשון שקפץ לי לראש היה משפט הסינוסים שזכרתי רק במעורפל - משהו עם היחס בין צלע ובין סינוס של זווית שקשורה אליה וכל זה מתקשר איכשהו לרדיוס המעגל שחוסם את המשולש. כאן ברור מה המשולש הרלוונטי: \(ABD\) למשל, שבו הצלע \(AD\) היא השוק שצריך לחשב ואילו \(\angle DAB\) היא הזווית שחישבנו במאמץ בסעיף הקודם. אז אני מגגל "משפט הסינוסים" ומקבל ש-\(\frac{AD}{\sin\angle DBA}=2R\). הבעיה היא שלא ידעתי מהי הזווית \(\angle DBA\). וכאן נתקעתי. נתקעתי להמון המון זמן וחשבתי על כל מני דרכים שונות ומשונות והשתגעתי.
ואז חזרתי לתרגיל אחר כך והתחלתי בכך שאני מצייר את כל הקווים שמחברים את קודקודי הטרפז עם מרכז המעגל \(O\). מה קיבלנו? את המשולש \(ODA\) שהוא שווה שוקיים (\(AO=DO=R\)). אני יודע מהי זווית הראש שלו כי חישבתי אותה בסעיף הקודם - \(180^{\circ}-2\alpha\). אני יודע מה זווית הבסיס, אם כן: \(\alpha\) כל אחת מהן. עכשיו אפשר להשתמש במשפט הסינוסים: \(\frac{AO}{\sin\angle ODA}=\frac{R}{\sin\alpha}=\frac{AD}{\sin\angle AOD}=\frac{AD}{\sin\left(180^{\circ}-2\alpha\right)}=\frac{AD}{\sin2\alpha}\) (בשביל להיזכר מה זה \(\sin\left(180^{\circ}-x\right)\) שירטטתי לעצמי את הגרף של סינוס והזכרתי לעצמי ש-\(\sin\left(180^{\circ}-x\right)=\sin x\); אני לא זוכר את זה אוטומטית אלא רק יודע שיש משהו בסגנון ואפשר לבדוק אותו). מסקנה: \(AD=\frac{\sin2\alpha}{\sin\alpha}R=\frac{2\sin\alpha\cos\alpha}{\sin\alpha}R=2\cos\alpha R\) (את הזהות \(\sin2\alpha=2\sin\alpha\cos\alpha\) אני כן זוכר בעל פה, עוד מתקופת התיכון, והיא הייתה שימושית פה ושם גם באוניברסיטה).
סעיף ג'
זה היה פשוט קצת יותר. מורידים את הגובה מ-\(D\) אל \(AB\) ומקבלים משולש ישר זווית שהיתר שלו הוא \(DA\) ואורך הצלע שמול הזווית \(\angle DAB\) הוא \(h\). כלומר קיבלנו \(\frac{h}{DA}=\sin\angle DAB=\sin\left(90^{\circ}-\frac{\alpha}{2}\right)=\cos\frac{\alpha}{2}\) (את הזהות \(\sin\left(90^{\circ}-x\right)=\cos x\) אני זוכר בע"פ). לכן \(DA=\frac{h}{\cos\frac{\alpha}{2}}\).
סעיף ד'
אני יודע שהמשולש \(COD\) הוא שווה שוקיים עם אורך שוק \(R\) ושזווית הראש היא \(\alpha\). האם זה עוזר לי למצוא את השטח שלו? לא עולה לי לראש נוסחה סטנדרטית לשטח של מעגל בסיטואציה כזו. אני כן יודע את הדרך הסטנדרטית לחשב שטח של משולש - גובה לצלע כפול אורך הצלע חלקי 2. אני מניח שאפשר בזריזות עם בניית עזר לקבל מזה נוסחה טריגונומטרית, אז אני מגגל "שטח משולש טריגו" ולא מתאכזב - שטח משולש עם צלעות \(a,b\) וזווית \(\alpha\) ביניהן הוא פשוט \(\frac{ab\sin\alpha}{2}\). כלומר במקרה שלנו שטח המשולש הוא \(\frac{R^{2}\sin\alpha}{2}\).
הבעיה היא ששטח המשולש נתון לי כ-\(\frac{h^{2}}{12\cos^{2}\frac{\alpha}{2}}\). כלומר, יש פה \(h\) במקום \(R\). אבל אני לא מודאג כי בשני הסעיפים הקודמים הבעתי את אותה צלע באמצעות \(R,h\) כך שאני יודע שיש קשר ביניהם. בואו נכתוב אותו:
\(2\cos\alpha R=\frac{h}{\cos\frac{\alpha}{2}}\)
כלומר:
\(R=\frac{h}{2\cos\alpha\cos\frac{\alpha}{2}}\).
לכן:
\(R^{2}=\frac{h^{2}}{4\cos^{2}\alpha\cos^{2}\frac{\alpha}{2}}\)
לכן שטח המשולש הוא:
\(\frac{R^{2}\sin\alpha}{2}=\frac{h^{2}\sin\alpha}{8\cos^{2}\alpha\cos^{2}\frac{\alpha}{2}}=\frac{h^{2}}{12\cos^{2}\frac{\alpha}{2}}\)
מכאן אני יכול להסיק:
\(\frac{\sin\alpha}{8\cos^{2}\alpha}=\frac{1}{12}\)
כלומר:
\(\frac{\sin\alpha}{\cos^{2}\alpha}=\frac{2}{3}\)
כלומר \(\frac{\tan\alpha}{\cos\alpha}=\frac{2}{3}\).
איך זה מקדם אותי לקראת מציאת \(\alpha\)? אין לי מושג. איך פותרים משוואה כזו? זה השלב שבו אני מסתכל שוב על כל החישובים שלי כדי לוודא שלא פספסתי משהו. אולי הסינוס במונה היה צריך להיות בריבוע בעצמו, או משהו?
בואו ננסה גישה אחרת. אני זוכר את הזהות \(\sin^{2}\alpha+\cos^{2}\alpha=1\), כלומר אני יכול לכתוב \(\frac{\sin\alpha}{\cos^{2}\alpha}=\frac{\sin\alpha}{1-\sin^{2}\alpha}\). אה, יופי! זה מקדם אותי אל עבר משהו שנראה כמו משוואה ריבועית! בואו נסמן \(x=\sin\alpha\), אז קיבלנו
\(\frac{x}{1-x^{2}}=\frac{2}{3}\)
כלומר:
\(3x=2-2x^{2}\)
כלומר
\(2x^{2}+3x-2=0\)
את המשוואה הזו קל לפתור עם נוסחת השורשים:
\(x_{1,2}=\frac{-3\pm\sqrt{9+16}}{4}=\frac{-3\pm5}{4}=\frac{1}{2},-2\)
הפתרון של \(x=-2\) בבירור לא רלוונטי כי סינוס מחזיר מספר בין \(-1\) ל-1. לכן קיבלנו \(\sin\alpha=\frac{1}{2}\) ואת זה אני זוכר בעל פה ולא צריך מחשבון - \(\alpha=30^{\circ}\). יש מעט מאוד ערכים של סינוס שאני זוכר בעל פה, כי אפשר לתת להם תיאור ציורי נחמד:
- \(\sin0^{\circ}=\frac{\sqrt{0}}{2}\)
- \(\sin30^{\circ}=\frac{\sqrt{1}}{2}\)
- \(\sin45^{\circ}=\frac{\sqrt{2}}{2}\)
- \(\sin60^{\circ}=\frac{\sqrt{3}}{2}\)
- \(\sin90^{\circ}=\frac{\sqrt{4}}{2}\)
זה עוד משהו שאני זוכר בעל פה עוד מהתיכון.
מה דעתי על השאלות?
במשפט אחד: השאלות הללו הרגישו לי קצת כמו מה שעושים כשפותרים תרגילים במתמטיקה אוניברסיטאית, וזה לאו דווקא דבר טוב.
מה שיש כאן הוא זה: אנחנו נדרשים לגוף ידע לא אלמנטרי כלשהו (תראו כמה פעמים נזקקתי לגוגל) ואז נתונה לנו בעיה שצריך ליישם את הידע הזה עליה. לא תמיד ברור איך ליישם אותו ומאיזה כיוון לתקוף את הבעיה. ברוב המקרים זה היה לי יחסית ברור והצלחתי לפתור די מהר, אבל במקרה אחד (שאלה 5 סעיף ב') נתקעתי להמון זמן. בכך גם ראיתי שלא למדתי את הלקח שלי מהמבחנים באוניברסיטה: כשנתקעים בשאלה כלשהי הדבר הקריטי ביותר לעשות הוא לעבור לשאלה אחרת. כך גם מספיקים לפתור את יתר המבחן וגם מקבלים הפסקה מהשאלה הקשה וכשחוזרים אליה ייתכן שניקוי הראש הזה יאפשר לפתור אותה בקלות. זה בדיוק מה שקרה כאן - כל עוד שברתי את הראש על השאלה וניסיתי לפתור בגישה הלא נכונה שנתקעתי בה, לא הגעתי לכלום. כשבאתי אל השאלה שוב אחר כך וניסיתי לפתור אותה מאפס, פתרתי מייד. זה נשמע כמו דבר אלמנטרי לחלוטין וכמו טקטיקה בסיסית ביותר בפתרון מבחנים, אבל איכשהו יוצא שקל כל כך להתעלם ממנה, וזה לרוב מוביל לאסון.
אז אם זה טוב, מה בעצם רע? שני דברים. ראשית, היישום של גוף הידע שלנו הוא לפתרון בעיות שנראות מלאכותיות לגמרי. במבחנים במתמטיקה לרוב (לא תמיד) יש איזה רעיון לא שרירותי בתוך כל שאלה שמסייע לתת כיוון כלשהו לאופן שבו כדאי לתקוף אותה. כאן לא ממש הרגשתי את זה. זה היה יותר "בואו נזרוק דברים על הקיר ונראה מה נדבק". אני חושב שזה נגרם מכך שמלכתחילה ה"עולם" שעליו מדברים כאן - גאומטריה אוקלידית - הוא כזה שברמה הנלמדת לא מספק תעלומות עם עניין גדול במיוחד. אבל אולי אני טועה.
הבעיה השניה כנראה הרבה פחות רלוונטית לתלמידי תיכון והרבה יותר רלוונטית לי אישית - בעוד שבמתמטיקה אוניברסיטאית קל יחסית לשלוט ברוב החומר כי אין צורך לשנן אותו במפורש (כמובן, יש כאלו שעושים את זה) אלא ניתן להסתפק בזכרון של הרעיונות הכלליים והסתמכות על היכולת לפתח דברים מחדש כמעט מייד כשיהיה צורך (למשל, איך הצלחתי להיזכר ש-\(\sin\left(180^{\circ}-x\right)=\sin x\)? לא זכרתי את זה בעל פה). עבור רוב הדברים בגאומטריה אין לי את זה. הקטע הזה של מרובע שחסום במעגל וסכום כל זוג זוויות נגדיות בו הוא \(180^{\circ}\)? אולי ידעתי את זה פעם אבל שכחתי, ולא הייתה לי שום נקודת מוצא, שום תחושה, שתאפשר לי לגלות את זה מחדש. הייתי חייב לגגל. אני מאמין שאם אני הייתי לומד גיאומטריה בצורה שונה בתיכון, או לא הייתי מתרשל בתפקידי כבעל בלוג מתמטי ולומד אותה באופן מסודר כמבוגר (מתי תהיה סדרת פוסטים על "יסודות" של אוקלידס?) זה לא היה המצב.
האם צריך שאלות כמו אלו במבחן? מצד אחד, הן באמת בודקות יכולת פתרון בעיות שמזכירה את פתרון הבעיות שסטודנט למתמטיקה מתמודד איתן; מצד שני, האם אנחנו באמת רוצים לבחון תלמידי תיכון על הדבר הזה? לא יודע.
שאלה 6
אה. חדו"א. איזה כיף. ניחוש שלי מראש: יהיה לי קל. יהיה לי טכני ומגעיל. לא סותר.
סעיף א'
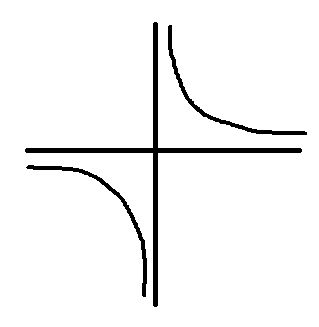
הפונקציה היא \(f\left(x\right)=\frac{2\cos^{2}x-1}{2\cos^{2}x}\). הסכנה היחידה שהיא עומדת בפניה היא התאפסות של המכנה. בתחום \(0\le x\le\frac{\pi}{2}\) (ראיתם? עברתי לרדיאנים! הא!) \(\cos x\) מתאפס רק בנקודה אחת - \(x=\frac{\pi}{2}\). לכן הפונקציה מוגדרת בתחום \(0\le x<\frac{\pi}{2}\).
אסימפטוטה מאונכת לציר \(x\)...? תזכירו לי מה זה? הכוונה לקווים ישרים, מהצורה \(x=a\), שהפונקציה שואפת לאינסוף כששואפים אליהם? אם כן, שאיפה לאינסוף מתקיימת רק כששואפים אל \(a=\frac{\pi}{2}\): במקרה הזה המכנה שואף ל-\(0^{+}\) והמונה שואף ל-\(-1\), כך שהפונקציה שואפת למינוס אינסוף (גרפית היא תגלוש כלפי מטה... אה, שיט, הולכים לבקש ממני לשרטט בהמשך, נכון?)
בשביל חיתוך עם ציר \(x\) צריך שהפונקציה תתאפס, כלומר שהמונה יתאפס. כלומר שואלים מה פתרונות המשוואה \(2\cos^{2}x=1\), כלומר \(\cos x=\pm\sqrt{\frac{1}{2}}=\pm\frac{\sqrt{2}}{2}\). אמרתי שאני זוכר ערכים בע"פ קודם, נכון? אז \(x=\frac{\pi}{4}\) הוא פתרון למשוואה החיובית. האם יש עוד פתרון בתחום הרלוונטי? ובכן, אני זוכר איך \(\cos\) נראית בו: היא מתחילה מ-1 ב-\(x=0\) ויורדת עד ל-\(0\) ב-\(\frac{\pi}{2}\). בדרך היא עוברת ב-\(\frac{\sqrt{2}}{2}\) אבל לא עוברת ב-\(-\frac{\sqrt{2}}{2}\) ולכן אין לנו נקודת חיתוך נוספת בתחום הזה.
כאן אני צריך רגע כדי להיזכר בנוסחאות הרלוונטיות. אנחנו נצטרך לגזור פונקציה שהיא מנה - אני זוכר בעל פה את הנוסחה \(\left(\frac{f}{g}\right)^{\prime}=\frac{f^{\prime}g-fg^{\prime}}{g^{2}}\) ולוקח שניה כדי לוודא לעצמי בראש שהיא נכונה (נובעת מהנוסחה \(\left(fg\right)^{\prime}=f^{\prime}g+fg^{\prime}\) שאין לי ספקות לגביה). כמובן, במבחן אמיתי יש את זה בדף הנוסחאות... אני מתחיל להפעיל את זה על הפונקציה שלנו, אבל אז עוצר - למה להסתבך? המונה והמכנה מאוד דומים. אפשר לפשט את הפונקציה: \(f\left(x\right)=1-\frac{1}{2\cos^{2}x}\). עכשיו יהיה הרבה יותר קל לגזור. כשיש 1 במונה הנוסחה לנגזרת הופכת להיות \(\left(\frac{1}{f}\right)^{\prime}=\frac{-f^{\prime}}{f^{2}}\), ולכן אחרי גזירה נקבל \(\frac{4\cos x\sin x}{4\cos^{4}x}=-\frac{\sin2x}{2\cos^{4}x}\)-. הפונקציה הזו מתאפסת כש-\(x=0\). המונה מתאפס גם כש-\(x=\frac{\pi}{2}\) אבל הנקודה הזו היא לא חלק מתחום ההגדרה כך שהיא לא רלוונטית, וממילא המכנה מתפוצץ גם בנקודה הזו. אז נקודת הקיצון היחידה שלנו היא ב-\(x=0\). כדי למצוא את סוג נקודת הקיצון צריך לגזור שוב ולראות אם הנגזרת השניה שלילית (נקודת מקסימום, כי מהנקודה הזו והלאה הפונקציה תתחיל לרדת - הנגזרת השניה שלילית ולכן הנגזרת הראשונה שהיא כרגע אפס תהפוך לשלילית בעצמה והפונקציה תתחיל לרדת) או חיובית (נקודת מינימום) או אפס (במקרה הזה עדיין לא בטוח מה הנקודה - עבור \(f\left(x\right)=x^{3}\) זו נקודת פיתול, אבל עבור \(f\left(x\right)=x^{4}\) זו נקודת מינימום - תהרגו אותי אם אני יודע מאיפה אני זוכר את זה). אני זוכר טריק מהתיכון - מכיוון שהמכנה הוא ריבוע, הוא תמיד אי-שלילי. לכן, כדי לדעת את הסימן, מספיק לחשב את המונה. המונה הולך לצאת \(-\left(2\cos2x\cdot2\cos^{4}x-\sin2x\cdot\left(-8\cos^{3}x\sin x\right)\right)\). נציב \(x=0\) ונישאר עם \(-4\) - שלילי, לכן זו נקודת מקסימום. כמובן, אני לא מאמין לזה באופן עיוור. בואו נסתכל על הפונקציה: \(f\left(x\right)=1-\frac{1}{2\cos^{2}x}\). כאשר \(x=0\) הערך של הפונקציה יהיה \(\frac{1}{2}\). ככל שנתרחק מ-\(x=0\) הערך של \(\cos^{2}x\) יקטן, ולכן השבר כולו יגדל ולכן הערך של 1 כשמחסרים אותו מהשבר יקטן. אם כן, נקודת מקסימום נשמעת סבירה.
סעיף ב'
עכשיו מרחיבים לנו פתאום את תחום ההגדרה וזה מאוד מצער כי מה עם כל החישובים שעשינו? ובכן, סעיף 1 פה בא להגיד לנו שמה שעשינו עד כה מספיק: פונקציה זוגית היא פונקציה שמקיימת \(f\left(-x\right)=f\left(x\right)\). בואו נוכיח שזה קורה: \(f\left(-x\right)=1-\frac{1}{2\cos^{2}\left(-x\right)}=1-\frac{1}{2\cos^{2}x}=f\left(x\right)\) - אין כאן חוכמה, רק שימוש בזהות \(\cos\left(-x\right)=\cos x\) שאני גם זוכר בעל פה וגם קל להיזכר בה אם זוכרים את הגרף של קוסינוס.
אז עכשיו לשרטוט. בגלל שהפונקציה היא זוגית אני אשרטט משהו סימטרי ביחס לציר \(y\). מה הדברים שאני מתחשב בהם בשרטוט? ב-\(0\) יש לי נקודת מקסימום בגובה חצי. ב-\(\frac{\pi}{4}\) יהיה חיתוך עם ציר \(x\). ב-\(\frac{\pi}{2}\) תהיה אסימפטוטה אנכית. אז נראה שזה יהיה גרף פשוט - גבעה כזו שצונחת עד אינסוף. הנה השרטוט האומלל שלי:
סעיף ג'
שטח? זה שם קוד לאינטגרל פה. "ברביע הראשון" זה אומר להסתכל על התחום \(0\le x\le\frac{\pi}{4}\), כי ערכי \(x\) קטנים יותר מוציאים אותנו מהרביע הראשון אל הרביע השני, ועבור ערכי \(x\) גדולים יותר ערכי הפונקציה שליליים ולכן נהיה ברביע הרביעי. אז בואו נחשב: \(\int_{0}^{\frac{\pi}{4}}\left(1-\frac{1}{2\cos^{2}x}\right)dx\)
אה... שניה. איך אני עושה אינטגרל כזה? מה הולך פה? האינטגרלים בתיכון לא אמורים להיות הכי אלמנטריים שאפשר?
הקושי שלי הוא בתכל'ס עם האינטגרל \(\int\frac{1}{\cos^{2}x}dx\), ואינטואיטבית מה שמפריע לי הוא שאין כאן סינוס שבו כופלים או משהו דומה. הרי \(\frac{1}{\cos^{2}x}\) מזכיר את מה שמקבלים בנגזרת של מנה, כשבמכנה המקורי יש \(\cos x\). אבל מה יהיה במונה? ובכן, האינטואיציה שלי היא שכדאי להשתמש ב-\(\sin^{2}x+\cos^{2}x=1\) כי זה יתן לי במונה משהו שכבר נראה בדיוק כאילו הגיע מתוך נגזרת. אז בואו נכתוב \(\frac{\sin^{2}x+\cos^{2}x}{\cos^{2}x}\) - עכשיו אני פשוט מנחש שזו הנגזרת של \(\frac{\sin x}{\cos x}\). גזירה מהירה מאששת את החשד הזה - אבל איך תלמידי תיכון אמורים לעלות על זה? לא יודע. מעניין אם מלמדים אותם לנחש.
אם כן, אני מקבל:
\(\int_{0}^{\frac{\pi}{4}}\left(1-\frac{1}{2\cos^{2}x}\right)dx=\frac{\pi}{4}-\frac{1}{2}\int_{0}^{\frac{\pi}{4}}\frac{1}{\cos^{2}x}dx=\frac{\pi}{4}-\left[\frac{\sin x}{\cos x}\right]_{0}^{\frac{\pi}{4}}=\frac{\pi}{4}-1\)
האם קיבלתי תוצאה שנשמעת הגיונית? האם זה מספר חיובי? ובכן, לא ממש! \(\pi<4\) ולכן קיבלתי מספר שלילי. זה לא הגיוני - יש לי טעות איפה שהוא. עיון חוזר בחישוב שעשיתי מגלה ששכחתי את המקדם של ה-\(\frac{1}{2}\) שבו כופלים את האינטגרל המפושט. הייתי צריך לקבל תוצאה סופית \(\frac{\pi}{4}-\frac{1}{2}\), שהיא כן הגיונית. אני משאיר בכוונה את הטעות הזו בפתרון שלי כדי לציין במפורש נקודה טריוויאלית: אני טועה בחישובים. כל הזמן. למזלי התרגלתי לבדוק האם התוצאות שלי הגיוניות, וזה עוזר לי מאוד למצוא טעויות פה ושם, כמו עכשיו.
הערה קטנה לסיום: חשבתי כמה פעמים במהלך התרגיל להשתמש בזהות שאני זוכר במעורפל, \(\cos^{2}x=\frac{1+\cos2x}{2}\). זה אפילו נראה כאילו \(f\left(x\right)\) הונדסה כדי שנשתמש בזהות הזו כדי לפשט אותה על ההתחלה. בסוף לא הרגשתי צורך להשתמש בה בשום מקום. אולי זו טעות.
שאלה 7
סעיף א'
זו שאלה... מעניינת! אני לא זוכר משהו דומה לזה בזמני. כאן יש לנו פונקציה שלא נתונה בצורה מפורשת אלא רק על ידי גרף וצריך להסיק דברים עליה.
מה שרואים מייד על הפונקציה היא שעבור \(x>0\) הפונקציה היא מונוטונית עולה, ועבור \(x<0\) היא מונוטונית יורדת. כלומר, הנגזרת חיובית עבור \(x>0\) ושלילית עבור \(x<0\). עכשיו, האם הנגזרת קבועה או משתנה? נגזרת קבועה באה לידי ביטוי בפונקציה לינארית, וכאן זה בבירור לא המצב. עבור \(x>0\) ככל ש-\(x\) שואף ל-0 כך הנגזרת שואפת לאינסוף, ואילו כאשר \(x\) שואף לאינסוף, הנגזרת שואפת לאפס. לכן הנגזרת עצמה היא מונוטונית יורדת. בדומה, עבור \(x<0\), הנגזרת (השלילית) תצא מונוטונית יורדת - שואפת לאפס כש-\(x\) שואף למינוס אינסוף, שואפת למינוס אינסוף כש-\(x\) שואף ל-\(0\). אז הנה סקיצה:
עכשיו צריך לשחק את אותו המשחק גם עם הנגזרת השניה. בואו נחשוב על זה לרגע: בשני המקרים, \(x>0\) וגם \(x<0\), הנגזרת יורדת. כך שהנגזרת השניה תמיד שלילית. כאשר \(x>0\) קצב הירידה מתחיל גדול והולך וקטן עם הזמן, כלומר הנגזרת השלילית הולכת וגדלה (הולכת ומתקרבת לאפס) עד שהיא שואפת לאפס באינסוף (ולמינוס אינסוף באפס). כאשר \(x<0\) קורה אותו הדבר: במינוס אינסוף, הנגזרת שואפת לאפס, בעוד שבאפס היא שואפת למינוס אינסוף. זה נותן לי את הסקיצה הבאה:
סעיף ב'
זה ממשיך להיות מעניין. עכשיו נותנים לנו את (הערך המוחלט של) האינטגרל המסוים של הנגזרת השניה בין \(x=1\) ובין \(x=2\) ומבקשים שנגיד מה ההפרש בין ערכי הנגזרת הראשונה בין שתי הנקודות הללו (אני קצת מתרגם לעברית את הניסוח הגאומטרי שלהם). לי ברור מייד שהתשובה היא פשוט 5.25, כי זו המהות של המשפט היסודי של החדו"א: \(5.25=\int_{1}^{2}g^{\prime\prime}\left(x\right)dx=g^{\prime}\left(2\right)-g^{\prime}\left(1\right)\). במילים אחרות, אין כאן בכלל שאלה חישובית אלא סתם שאלה של "נראה אם הבנתם את החומר". אני מתרשם. אני באמת מתרשם. לא זכור לי משהו כזה בזמני.
סעיף ג'
גם הסעיף הזה מעניין. אומרים לנו ש-\(y=\frac{a}{x^{3}}\) מתאר אחת מבין שלוש הפונקציות שלנו (הפונקציה, הנגזרת הראשונה והנגזרת השניה שלה). ראשית מבקשים לגלות איזו מבין השלוש היא, אם ידוע ש-\(a>0\). כדי לפשט את המחשבה מספיק להסתכל על \(\frac{1}{x^{3}}\) ולשאול את עצמנו לאיזו פונקציה יש גרף שדומה לאלו שראינו. ראשית, אם \(x>0\) אז \(\frac{1}{x^{3}}>0\) ולכן זו בוודאי לא יכולה להיות הנגזרת השניה. שנית, אם \(x<0\) אז \(\frac{1}{x^{3}}<0\) ולכן זו גם לא יכולה להיות \(g\), שהיא לא שלילית לכל \(x<0\). אז מן הסתם \(g^{\prime}=\frac{a}{x^{3}}\). כעת מבקשים שנחשב את \(a\), ואת זה קל לעשות עם הסעיף הקודם: \(\frac{21}{4}=\frac{a}{8}-\frac{a}{1}\) ולכן נקבל \(\frac{21}{4}=a\left(\frac{1}{8}-1\right)\) וזה... רגע, זה לא מסתדר לי. אני מקבל בסוף משהו שלילי ואמרו ש-\(a\) חיובי. אה, כמובן, איזו טעות מגוחכת שלי.
בואו ניזכר שניה מה קרה בסעיף הקודם. טענתי ש-\(g^{\prime}\left(2\right)-g^{\prime}\left(1\right)=5.25\) בגלל המשפט היסודי של החדו"א, אבל שכחתי שם שרגע לפני כן אמרתי בעצמי שה-5.25 הוא לא האינטגרל \(\int_{1}^{2}g^{\prime\prime}\left(x\right)dx\) אלא הערך המוחלט שלו. זה נגרם בגלל שהם נותנים לי את "השטח שכלוא בין כך וכך" אבל אינטגרל על פונקציה שלילית (כמו \(g^{\prime\prime}\)) לא נותן את השטח אלא את מינוס השטח. בקיצור, מה שקיבלתי הוא ש-\(g^{\prime}\left(1\right)-g^{\prime}\left(2\right)=5.25\) - ועכשיו אני רואה שזה מה שביקשו מאיתנו בסעיף ב' אז התשובה שלי בו עדיין נכונה. רק פה אני צריך לבצע היפוך, ולקבל \(\frac{21}{4}=a\left(1-\frac{1}{8}\right)\), כלומר \(a=\frac{21}{4}\cdot\frac{8}{7}=6\).
שאלה 8
סעיף א'
זה נראה כמו שאלת מינימום ומקסימום פשוטה כשהסעיף הראשון הזה הוא יותר הכוונה מאשר אתגר אמיתי. יש לי משולש \(ABC\) ישר זווית כך ש-\(BC=k\) ו-\(AB=x\) ומבקשים תיאור של \(BC\) באמצעות \(k,x\). ובכן, אנחנו במשולש ישר זווית. אם לא נשתמש כאן בפיתגורס, מתי נשתמש? על כן \(BC=\sqrt{k^{2}-x^{2}}\).
סעיף ב'
עכשיו מדברים על "הערך המקסימלי של המכפלה \(BC\cdot AD^{2}\)". כאן החדו"א נכנס לעניין. אבל בשביל זה צריך לקבל ביטוי כלשהו ל-\(AD\). אנחנו יודעים ש-\(AB=x\) הוא יתר במשולש שווה שוקיים וישר זווית שבו \(AD\) הוא ניצב. במשולש כזה הזוויות הן \(45^{\circ}\) ולכן \(\frac{AD}{AB}=\sin45^{\circ}=\frac{\sqrt{2}}{2}\), כלומר \(AD=\frac{\sqrt{2}}{2}x\) ומכאן ש-\(AD^{2}=\frac{x^{2}}{2}\). המסקנה היא ש-\(f\left(x\right)=BC\cdot AD^{2}=\frac{x^{2}}{2}\sqrt{k^{2}-x^{2}}\). זו הפונקציה שצריך למצוא לה מקסימום. וואו, כמה שלא בא לי לגזור את זה. אולי טעיתי ובסעיף א' יש פתרון יותר יפה? אני לא רואה כזה דבר...
טוב, טוב, אני גוזר...
לא אלאה אתכם בפרטי הפעם הראשונה שבה גזרתי. השורה התחתונה - הייתה לי טעות חישוב מטופשת והרגשתי שמשהו משתבש רק כשהשוויתי את התוצאה שקיבלתי ל-\(3\sqrt{3}\) שנתון בשאלה ומשהו פה לא נראה לי אלגנטי. בפעם השניה כבר הייתי הרבה יותר זהיר - שמתי לב שהפונקציה שאני גוזר סתם מסובכת שלא לצורך וזה מגדיל את הסיכון לטעויות. יותר קל לי לעבוד עם כמה שפחות חזקות ומכפלות בקבועים. אז המצאתי את הפונקציה הבאה: \(g\left(t\right)=t\sqrt{m-t}\) והחלטתי לחקור אותה. כלומר, במקום \(x^{2}\) יש לי את \(t\), ובמקום \(k^{2}\) יש לי את \(m\) ואת החלוקה ב-2 העפתי לכל הרוחות כי היא לא משנה את נקודת המינימום/מקסימום. וכעת:
\(g^{\prime}\left(t\right)=\sqrt{m-t}-\frac{t}{2\sqrt{m-t}}=\frac{2\left(m-t\right)-t}{2\sqrt{m-t}}=\frac{2m-3t}{2\sqrt{m-t}}\)
רואים את ה-\(3t\) למעלה? זה מה שהיה חסר לי בפעם הקודמת. משום מה קיבלתי שם 2 במקום 3 כי ה-2 שבו צריך לכפול הלכה לאיבוד אי שם. עכשיו ברור מה נקודת המקסימום: כאשר \(2m=3t\), כלומר \(t=\frac{2}{3}m\), כלומר \(x^{2}=\frac{2}{3}k^{2}\). בואו נציב את זה חזרה בפונקציה המקורית ונקבל:
\(BC\cdot AD^{2}=\frac{2}{6}k^{2}\sqrt{k^{2}-\frac{2}{3}k^{2}}=\frac{1}{3}k^{3}\sqrt{\frac{1}{3}}=\frac{\sqrt{3}}{9}k^{3}\)
נשווה את זה ל-3 ונקבל \(\frac{\sqrt{3}}{9}k^{3}=3\sqrt{3}\), כלומר \(k^{3}=27\), כלומר \(k=3\). עכשיו המספרים מסתדרים!
נותר למצוא את השטח של \(ADB\). במשולש ישר זווית השטח הוא פשוט מכפלת שני הניצבים חלקי 2. כאן המשולש שווה שוקיים ולכן הניצבים שווים, כלומר השטח הוא \(\frac{AD^{2}}{2}\). כזכור, \(AD=\frac{\sqrt{2}}{2}x\) ולכן \(\frac{AD^{2}}{2}=\frac{1}{4}x^{2}=\frac{1}{4}\frac{2}{3}k^{2}=\frac{1}{2}\cdot\frac{1}{3}\cdot9=\frac{3}{2}\) וזה השטח (בסמ"ר, כי הם טרחו לתת יחידות קודם).
מה דעתי על השאלות?
שאלות 6 ו-8 אכן היו טכניות ומגעילות ועשיתי בהן טעויות חישוב מפגרות ולא התלהבתי מהן באופן כללי. בכנות, אני לא בטוח בשביל מה תלמידים צריכים את זה. שאלה 7, לעומת זאת, הייתה תענוג. היא לא דרשה חשיבה מתמטית יחסית כמו שאלות הגיאומטריה, אבל היא גם לא הייתה טכנית - נראה היה שהיא בודקת נטו את ההבנה של החומר, ולא את היכולת לפתור משוואות ולגזור על פי נוסחאות. כנראה שהייתי מעדיף לגלות שאלה כזו בתוך נושא אחר, אבל התרשמתי ממנה לטובה גם כאן. אני תוהה מה התלמידים חשבו עליה (בטח שנאו אותה ואמרו שהיא לא הוגנת).