קוסטים, משפט לגראנז' וחבורות מנה

בפוסט הקודם של תורת החבורות דיברנו על תתי-חבורות והזכרתי את משפט לגראנז'. המשפט אומר שאם \( G \) היא חבורה סופית, ו-\( H \) היא תת-חבורה שלה, אז \( \left|H\right||\left|G\right| \) - הסדר של \( H \) מחלק את הסדר של \( G \) (“סדר” של חבורה הוא מספר האיברים בה). כבר ראינו למשפט שני שימושים לא טריוויאליים - שכל חבורה מסדר ראשוני היא בהכרח ציקלית, ושאם לחבורה יש לכל היותר תת-חבורה אחת מכל סדר שמחלק את סדר החבורה, אז היא ציקלית. בפוסט הזה אני רוצה להוכיח את המשפט. ההוכחה תהיה מהסוג הטוב ביותר שאפשר - הוכחה שאנחנו נזקקים למושג חדש בשבילה, ומושג שיתגלה כשימושי, מועיל וחשוב מאין כמוהו בהמשך - המושג של קוסט (coset) של תת-חבורה.

קוסטים ומשפט לגראנז'

אישית, הרבה זמן לא הבנתי את המושג של קוסט, כי הכרתי את ההגדרה אבל לא את מה שהיא אומרת. אז נתחיל ממה שהיא אומרת, בנפנוף ידיים, ואז נראה דוגמאות: בהינתן חבורה \( G \) ותת-חבורה \( H \) שלה, קוסט של \( H \) הוא קבוצה שמתקבלת על ידי “הזזה” של \( H \). בואו נראה שתי דוגמאות שבהן אפשר להרגיש את המשמעות של “הזזה” כזו בידיים.

נתחיל עם החבורה החביבה עלי, \( \mathbb{Z} \). בפוסט הקודם ראינו למה אני אוהב את החבורה הזו - זוהי החבורה הציקלית היחידה. ראינו שכל תת-חבורה של \( \mathbb{Z} \) היא מהצורה \( n\mathbb{Z}=\left\{ 0,n,-n,2n,-2n,\dots\right\} \) של הכפולות של מספר טבעי \( n \) כלשהו. למשל, \( 2\mathbb{Z} \) היא חבורת הזוגיים. ומה על האי-זוגיים? בפוסט הקודם אמרתי שהם אינם חבורה, כי אינם סגורים לחיבור (ואינם כוללים את 0). אבל אפשר לחשוב עליהם בתור הזזה של הזוגיים צעד אחד ימינה. מספר זוגי הוא מספר מהצורה \( 2k \) עבור \( k\in\mathbb{Z} \), בעוד שמספר אי זוגי הוא מספר מהצורה \( 2k+1 \) עבור \( k\in\mathbb{Z} \). כלומר, כל אי זוגי מתקבל מזוגי על ידי הוספה של 1. במתמטית, אומרים שהאי-זוגיים הם קוסט של הזוגיים בתוך חבורת השלמים. את האי-זוגיים אפשר לסמן באופן מקוצר בתור \( 2\mathbb{Z}+1 \) - כאילו אנחנו מחברים 1 לכל תת-החבורה \( 2\mathbb{Z} \) (ניתן לסימון הזה פירוש פורמלי עוד מעט).

דבר דומה יקרה גם עם \( n=3 \). קבוצת כל המספרים שמתחלקים ב-3, \( 3\mathbb{Z} \), היא תת-חבורה של השלמים. קבוצת המספרים שמשאירים שארית 1 בחלוקה ב-3 היא לא תת-חבורה (אין את 0, אין סגירות) אבל היא קוסט של \( 3\mathbb{Z} \) ובדומה גם קבוצת המספרים שמשאירים שארית 2. את הקוסטים הללו מסמנים ב-\( 3\mathbb{Z}+1 \) וב-\( 3\mathbb{Z}+2 \). הבנתם את העיקרון.

בשלב הזה אתם אולי שואלים - מה אם מזיזים ב-0? ובכן, בואו נדבר על הזוגיים למשל: \( 2\mathbb{Z}+0=2\mathbb{Z} \) - הזזה באפס מותירה אותנו עם הזוגיים. בפרט, הזוגיים הם גם כן קוסט של עצמם; אין עם זה בעיה. כמו כן, \( 2\mathbb{Z}+2=2\mathbb{Z} \), כלומר גם הזזה במספר זוגי תיתן לנו את הקוסט של הזוגיים, והזזה ב-3 תיתן לנו את הקוסט של האי-זוגיים וכן הלאה. אותו קוסט יכול לפעמים להתקבל על ידי הזזה עבור יותר מערך אחד, ואין פה בעיה.

בואו נעבור לדוגמא אחרת, ציורית אף יותר, עם חבורה חדשה שטרם הצגתי - \( \mathbb{R}^{2} \). המישור. אוסף כל הנקודות מהצורה \( \left(a,b\right) \) כך ש-\( a,b\in\mathbb{R} \) וחיבור הוא “איבר-איבר”: \( \left(a,b\right)+\left(x,y\right)=\left(a+x,b+y\right) \). לא קשה לראות שזו חבורה. עכשיו, בואו נסתכל על תת-החבורה הבאה: \( H=\left\{ \left(a,0\right)\ |\ a\in\mathbb{R}\right\} \). קל לבדוק שזו אכן תת-חבורה, והיא שווה פשוט לציר \( x \) (האם זו חבורה ציקלית? יש אולי תחושה כזו, אבל לא: למשל, \( \left(1,0\right) \) הולך ליצור רק את האיברים מהצורה \( \left(n,0\right) \) כך ש-\( n\in\mathbb{Z} \), לא את כל הציר; חבורה ציקלית היא בהכרח בת-מניה ואילו \( H \) לא בת מניה).

עכשיו, בואו ניקח את \( H \) ונחבר לכל אבריה את \( \left(0,1\right) \) - וקטור היחידה האנכי. נקבל את מה שאסמן בתור \( H+\left(0,1\right)=\left\{ \left(a,1\right)\ |\ a\in\mathbb{R}\right\} \). הדבר הזה הוא הקו האופקי בגובה \( y=1 \). זו לא תת-חבורה כי אין סגירות, אבל אפשר לחשוב על זה בתור “עותק” של ציר \( x \) שפשוט הזזנו קצת למעלה. באופן דומה אם נחבר לכל אברי \( H \) את \( \left(1,1\right) \) עדיין נקבל את אותו קוסט בדיוק - תחשבו על מה שקורה כשאתם לוקחים קו ישר אינסופי ומרימים אותו למעלה, ומה קורה כשאתם מרימים אותו באלכסון למעלה ושמאלה - מכיוון שהקו אינסופי, תקבלו בסופו של דבר את אותו הדבר בדיוק. לכן, כל עוד נחבר ל-\( H \) איבר מהצורה \( \left(x,1\right) \), ולא משנה מהו \( x \), נקבל את אותו קוסט. בקרוב נדון עוד בשאלה הזו, “מי האיברים שכשמחברים אותם לתת-החבורה מקבלים את אותו קוסט”.

שאר הקוסטים של \( H \) הם שאר הישרים האופקיים, והשאלה עכשיו היא מה קורה עם תת-חבורות דומות אחרות. למשל, \( H=\left\{ \left(a,a\right)\ |\ \left(a\in\mathbb{R}\right)\right\} \). זה תרגיל נחמד להראות שקוסט כאן הוא תמיד מהצורה \( H+\left(x,0\right)=\left\{ \left(a+x,a\right)\ |\ a\in\mathbb{R}\right\} \) ויוצא שקוסט כזה הוא קו ישר עם שיפוע של 45 מעלות, כמו \( H \) עצמה, אבל שנקודת החיתוך שלו עם ציר \( x \) היא שונה מ-\( \left(0,0\right) \). זה גם מה שיקרה באופן כללי: כל ישר שעובר דרך הראשית הוא תת-חבורה של \( \mathbb{R}^{2} \), ולכל ישר כזה, הקוסטים הם כל הישרים המקבילים לו. הנה איור:

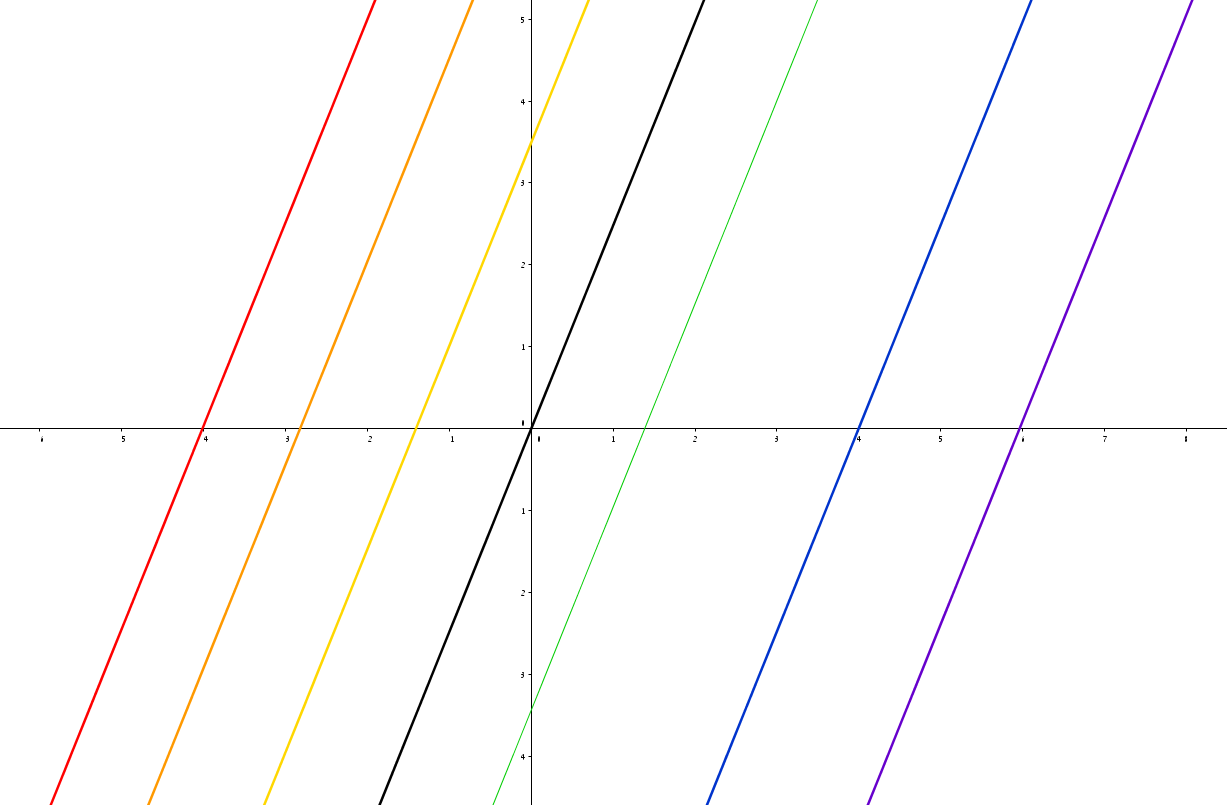
כאן תת-החבורה היא בשחור וחלק מהקוסטים האחרים שלה הם בצבעים עליזים. אני אומר חלק מהקוסטים כי אי אפשר לצייר את כולם - איחוד כל הקוסטים יתן לנו את כל המישור.

בואו נעבור כעת לפורמליזם. כזכור, כשאני מתאר חבורות כלליות אני משתמש בכפל, לא בחיבור, כדי לתאר את הפעולה של החבורה (להבדיל מהדוגמאות הקונקרטיות שהראיתי שבהן הפעולה הייתה ממש חיבור וכך היא סומנה) כמו כן, בדוגמאות שראינו החבורות היו אבליות (\( ab=ba \)) בזמן שבאופן כללי אנחנו לא מניחים שחבורות הן אבליות, וזה הולך להשפיע על הטרמינולוגיה. בהינתן חבורה \( G \), תת-חבורה \( H \) ואיבר \( a\in G \) אני מסמן:

\( aH\triangleq\left\{ ah\ |\ h\in H\right\} \)

\( Ha\triangleq\left\{ ha\ |\ h\in H\right\} \)

הקבוצה \( aH \) נקראת קוסט שמאלי של \( H \) והקבוצה \( Ha \) נקראת קוסט ימני של \( H \). צריך לשים לב לכך שקוסט יכול להיות בו זמנית גם שמאלי וגם ימני; אם החבורה היא אבלית זה בוודאי כך (\( aH=Ha \) לכל \( a,H \)) אבל גם בחבורה לא אבלית ייתכן שיתקיים \( aH=Ha \), או ייתכן שיתקיים \( aH=Hb \) עבור \( a\ne b \). נחזור לזה עוד מעט.

בדוגמאות שלנו שמנו לב, אינטואיטיבית, לשני דברים: אם \( H \) היא תת-חבורה של \( G \), אז:

• כל קוסט של \( H \) "נראה כמו" \( H \). בפרט, הוא נראה "מאותו גודל" כמו \( H \).
• אוסף כל הקוסטים של \( H \) מכסה את כל החבורה "בלי חפיפות".

השילוב של שתי התכונות הללו נותן לנו מייד את משפט לגראנז’. בואו ננסח אותן פורמלית.

התכונה הראשונה, פורמלית, פירושה שאם \( aH \) הוא קוסט של \( H \) (כנ”ל גם לקוסט ימני, אבל אני לא אטרח לעשות זאת במפורש, זו אותה הוכחה) אז קיימת פונקציה חח”ע ועל \( f:H\to aH \). בפרט, אם \( H \) סופית אז \( \left|H\right|=\left|aH\right| \). קל לנחש מה \( f \) אמורה להיות: \( f\left(h\right)=ah \). היא על פשוט בגלל ההגדרה של \( aH \). השאלה היא רק למה היא חח”ע, וזה נובע מהתכונה הבסיסית שהוכחתי בפוסט הראשון על חבורות: אם \( ax=ay \) אז \( x=y \).

כעת לתכונה השניה, שבעצם אומרת שני דברים. ראשית, שכל \( a\in G \) שייך לקוסט כלשהו של \( H \). זה די מובן מאליו: \( a\in aH \) שכן \( e\in H \) ולכן \( a=a\cdot e\in aH \). הדבר השני והמעניין יותר הוא שלא קיים \( a \) כך ש-\( a\in xH \) וגם \( a\in yH \) עבור \( xH\ne yH \). בואו נוכיח את זה בגישה “חיובית”: נניח ש-\( a\in xH \) ו-\( a\in yH \) ונוכיח שנובע מכך ש-\( xH=yH \).

אם כן, נניח ש-\( a\in xH \), כלומר קיים \( h_{1} \) כך ש-\( a=xh_{1} \). באופן דומה, מכיוון ש-\( a\in yH \) קיים \( h_{2} \) כך ש-\( a=yh_{2} \). זה אומר ש-\( xh_{1}=yh_{2} \), כלומר \( x=yh_{2}h_{1}^{-1} \). כעת, שימו לב לאיבר \( h_{2}h_{1}^{-1} \). מכיוון ש-\( H \) היא תת-חבורה, אנחנו יודעים שגם \( h_{2}h_{1}^{-1}\in H \) (אם \( H \) לא הייתה תת-חבורה כל הסיפור היה נשבר ברגע זה ממש). כעת בואו ניקח איבר כלשהו ב-\( xH \). הוא מהצורה \( xh=\left(yh_{2}h_{1}^{-1}\right)h=y\left(h_{2}h_{1}^{-1}h\right)\in yH \). קיבלנו ש-\( xH\subseteq yH \) ובאותו האופן מראים ש-\( yH\subseteq xH \), ומכאן ש-\( xH=yH \).

משפט לגראנז’ נובע כעת כמעט מאליו. מה שראינו הוא ש-\( G=\bigcup aH \) כאשר האיחוד נלקח על כל הקוסטים של \( H \) (דהיינו, אותו קוסט לא מופיע באיחוד פעמיים; אנחנו בוחרים \( a \) כלשהו כך ש-\( aH \) נותן את הקוסט, וחסל; אם יש עוד \( b \) כך ש-\( bH \) הוא אותו קוסט הוא לא ישתתף באיחוד כי לא צריך אותו). מכיוון שזה איחוד זר, אז במקרה של חבורה סופית, שבו יש מספר סופי של קוסטים, אפשר לכתוב \( \left|G\right|=\left|\bigcup aH\right|=\sum\left|aH\right| \) כאשר הסכום נלקח על כל הקוסטים. כעת, למספר הקוסטים של \( H \) ב-\( G \) יש שם מקובל: האינדקס של \( H \) ב-\( G \), וסימון מקובל: \( \left|G:H\right| \). מכיוון שראינו ש-\( \left|aH\right|=\left|H\right| \) נקבל את השוויון הבא: \( \left|G\right|=\left|G:H\right|\cdot\left|H\right| \). השוויון הזה הוא בדיוק משפט לגראנז’: הסדר של \( H \) מחלק את הסדר של \( G \), והמנה של החלוקה היא בדיוק האינדקס של \( H \) ב-\( G \). מה שכן, שימו לב שהאינדקס הוא מספר מעניין גם כש-\( G \) אינסופית; בהחלט ייתכן שיש תת-חבורה מאינדקס סופי גם כש-\( G \) אינסופית (למשל, האינדקס של \( 2\mathbb{Z} \) ב-\( \mathbb{Z} \) הוא 2, כפי שראינו).

עכשיו בואו נעצור, ננשום אוויר ונעבור לנושא שבהתחלה ייראה קצת לא קשור, אבל הוא כמובן קשור בצורה הדוקה ביותר למה שעשינו עד כה ונראה זאת עד סוף הפוסט.

חבורות מנה

עבור חבורה \( G \) ראינו דרך אחת להבין מה הולך בה - מסתכלים על תת-החבורות שלה. תת-חבורה הייתה תת-קבוצה של \( G \) שהפעולה הבינארית של \( G \) משרה עליה פעולה בינארית משל עצמה שביחס אליה היא חבורה. תת-חבורה, אם כן, היא מה שמקבלים כשמסלקים חלק מהאיברים ורואים מה קורה עם היתר. עכשיו אני רוצה לדבר על מושג נוסף, חשוב באותה מידה כמו תת-חבורה: חבורת מנה. חבורת מנה היא מה שמתקבל מ-\( G \) כשלוקחים איברים ובמקום לסלק אותם, אנחנו מאחדים אותם. פורמלית, מה קורה כשאנחנו לוקחים יחס שקילות על \( G \).

אם אתם מכירים יחסי שקילות, מצוין. אם לא, אני אנסה לתת את הדוגמה הכי יומיומית במתמטיקה שאני מכיר: מספרים רציונליים. מה זה מספר רציונלי אנחנו יודעים - “חצי” זה מושג שדי ברור לנו. אבל מהר מאוד כשמתחילים להתעסק עם מספרים כאלו רואים שיש לנו יותר מדרך אחת לכתוב “חצי”. אפשר לכתוב \( \frac{1}{2} \) ואפשר לכתוב \( \frac{2}{4} \) ואפשר לכתוב \( \frac{123}{246} \) וכן הלאה. מבחינתנו כל הביטויים הללו הם שקולים זה לזה - הם מייצגים את אותו דבר. פורמלית, כשאנחנו מדברים על המספרים הרציונליים אנחנו מסתכלים על הקבוצה \( \left\{ \frac{a}{b}\ |\ a\,b\in\mathbb{Z},b\ne0\right\} \) כש-\( \frac{a}{b} \) כאן לא בא לבטא פעולת חילוק (כי לא מוגדר לנו חילוק על \( \mathbb{Z} \) באופן כללי) אלא זהו פשוט סימון; ואז אנחנו באים ורוצים לומר שהסימון \( \frac{1}{2} \) והסימון \( \frac{2}{4} \) מסמנים את אותו הדבר. באופן כללי, \( \frac{a}{b} \) ו-\( \frac{c}{d} \) מייצגים את אותו דבר אם \( c\cdot b=a\cdot d \).

יחס שקילות מעל קבוצה \( A \) הוא אוסף של זוגות \( \left(x,y\right) \) כך ש-\( x,y\in A \), שמקיים שלוש דרישות: ראשית, לכל \( x\in A \) מתקיים ש-\( \left(x,x\right) \) שייך ליחס (רפלקסיביות). שנית, אם \( \left(x,y\right) \) שייך ליחס כך גם \( \left(y,x\right) \) (סימטריה) ולבסוף, אם \( \left(x,y\right) \) וגם \( \left(y,z\right) \)שייכים ליחס כך גם \( \left(x,z\right) \) (טרנזיטיביות).

אם \( R \) הוא יחס שקילות ו-\( x\in A \) הוא איבר כלשהו, מסמנים את קבוצת כל האיברים ששקולים ל-\( x \) על פי היחס \( R \) ב-\( \left[x\right]_{R}\triangleq\left\{ y\in A\ |\ \left(x,y\right)\in R\right\} \). לרוב אפילו סתם כותבים \( \left[x\right] \) אם ברור לאיזה \( R \) מתכוונים. לקבוצה כזו קוראים מחלקת שקילות. בהינתן מחלקה, כל איבר \( x \) כך ש-\( \left[x\right] \) היא המחלקה הזו נקרא נציג של המחלקה. בדוגמה שלנו, \( \left[\frac{1}{2}\right]=\left[\frac{2}{4}\right] \) וכדומה - מחלקת השקילות הזו מסמלת את המספר “חצי” עם נציגים כמו \( \frac{1}{2} \) ו-\( \frac{1}{4} \). כפי שאנחנו רואים, איברים שונים עשויים להגדיר את אותה מחלקת שקילות. קצת מזכיר את האופן שבו איברים שונים מגדירים את אותו קוסט, נכון?

את אוסף מחלקות השקילות של \( A \) על פי היחס \( R \) מסמנים ב-\( A/R \) וקוראים לו קבוצת המנה של \( A \) על פי \( R \). עכשיו, התכונות של יחס שקילות מבטיחות שקבוצת המנה תהיה נחמדה: ראשית, אין כזה דבר מחלקת שקילות ריקה; שנית, האיחוד של כל מחלקות השקילות נותן את כל \( A \); ולבסוף, אין חפיפה - שתי מחלקות שקילות הן זרות או זהות. פורמלית אומרים שקבוצת המנה מהווה חלוקה של \( A \). נשמע בדיוק כמו מה שקרה לנו עם קוסטים? כמובן, זה לא מקרי…

הכיוון השני גם נכון: כל חלוקה של \( A \) מגדירה יחס שקילות (שני איברים הם שקולים אם הם באותה קבוצה בחלוקה) כך שקבוצת המנה על פי יחס השקילות הזה היא החלוקה שממנה התחלנו. במילים אחרות, יחסי שקילות וחלוקות הן שתי דרכי ייצוג שונות לאותו הדבר, ואנחנו משתמשים במה שנוח לנו בכל רגע נתון.

איך כל זה קשור לחבורות? ובכן, חבורה היא גם קבוצה, אז אפשר להגדיר עליה שלל יחסי שקילות. למשל, על \( \mathbb{Z} \) בואו נגדיר את יחס השקילות שבו \( \left(x,y\right) \) שקולים אם ורק אם \( xy\ge1 \) או ש-\( x=y=0 \). ליחס הזה יש שלוש מחלקות שקילות: החיוביים \( \mathbb{Z}^{+} \), השליליים \( \mathbb{Z}^{-} \) ו-\( \left\{ 0\right\} \). וכעת אני מתעניין בשאלה הבאה: האם קבוצת המנה של \( \mathbb{Z} \) על פי יחס השקילות הזה היא חבורה?

ובכן, אנחנו כבר יודעים שיש בדיוק חבורה אחת עם שלושה איברים, \( \mathbb{Z}_{3} \), ואפשר להגדיר פעולה על מחלקות השקילות בהתאם. למשל לומר ש-\( \mathbb{Z}^{+}\cdot\mathbb{Z}^{+}=\mathbb{Z}^{-} \) וש-\( \left\{ 0\right\} \) הוא איבר היחידה וכדומה. אבל אנחנו מרגישים שזה לא מעניין: לקחנו קבוצה \( \mathbb{Z} \) שהיא גם חבורה, חילקנו אותה למחלקות שקילות, ואז הגדרנו פעולה חדשה על מחלקות השקילות מהראש שלנו. זה שהתחלנו מראש עם חבורה לא בא לידי ביטוי - הפעולה של החבורה המקורית לא באה לידי ביטוי בבניה שלנו, אז מה עשינו פה?

השאלה היא, כמובן, באיזה מובן אני רוצה שהפעולה של החבורה המקורית תבוא לידי ביטוי. אז הנה ההצעה שלי, שתשפיע על כל מה שנעשה מכאן והלאה: אם יש לי חבורה \( G \) ויחס שקילות \( R \) שמוגדר עליה, אני רוצה למצוא פעולת כפל על מחלקות השקילות של \( G \) באופן כזה שכדי לכפול שתי מחלקות שקילות מה שאפשר יהיה לעשות הוא לבחור נציג לכל מחלקת שקילות, לכפול את הנציגים על פי הפעולה של \( G \), ואז לקחת את מחלקת השקילות של התוצאה. פורמלית, אני רוצה שיתקיים \( \left[a\right]\cdot\left[b\right]=\left[ab\right] \), ואני רוצה שבמקרה הזה, קבוצת המנה תהווה חבורה ביחס לפעולה הזו.

מהדרישה הזו נובע המון על יחס השקילות \( R \) עצמו - מה הוא בדיוק יכול להיות ואיך הוא צריך להתנהג. ראשית, שימו לב לכך שאם נציב \( b=e \) נקבל שצריך להתקיים \( \left[a\right]\cdot\left[e\right]=\left[a\cdot e\right]=\left[a\right] \). זה אומר ש-\( \left[e\right] \) הולך להיות איבר היחידה של חבורת המנה. באופן דומה, \( \left[a\right]\cdot\left[a^{-1}\right]=\left[aa^{-1}\right]=\left[e\right] \) ולכן \( \left[a^{-1}\right]=\left(\left[a\right]\right)^{-1} \) - ההופכי של מחלקת השקילות של \( a \) מיוצג על ידי ההופכי של \( a \).

כעת, בואו ניקח \( x,y\in\left[e\right] \) כלשהם. אז \( \left[xy^{-1}\right]=\left[x\right]\cdot\left[y\right]^{-1}=\left[e\right]\cdot\left[e\right]^{-1}=\left[e\right] \) (כאן אני משתמש בכך שאם \( x\in\left[e\right] \) אז \( \left[x\right]=\left[e\right] \)). במילים: אם \( x,y\in\left[e\right] \) אז גם \( xy^{-1}\in\left[e\right] \). את הדבר הזה ראינו בפוסט הקודם - המשמעות שלו היא ש-\( \left[e\right] \) היא תת-חבורה של \( G \). אז בואו נסמן \( H=\left[e\right] \) מעתה ואילך.

כעת, בואו נניח ש-\( \left[a\right]=\left[b\right] \), כלומר \( a,b \) שקולים זה לזה. אז \( \left[b\right]^{-1}\left[a\right]=\left[e\right] \) (כפלתי את שני האגפים ב-\( \left[b\right]^{-1} \)), כלומר \( \left[b^{-1}a\right]=\left[e\right] \), כלומר \( b^{-1}a\in H \). אפשר גם להפוך את כיוון הגרירות ולקבל שאם \( b^{-1}a\in H \) אז \( \left[a\right]=\left[b\right] \). במילים אחרות, קיבלנו שאם עבור יחס שקילות כלשהו קבוצת המנה שמקבלים היא חבורה עם הפעולה שמושרית מ-\( G \), אז יחס השקילות חייב להיות מהצורה הבאה: קיימת תת-חבורה \( H \) של \( G \) כך ש-\( a,b \) שקולים אם ורק אם \( b^{-1}a\in H \).

אם זהו יחס השקילות, האם יש לנו תיאור מפורש של מחלקות השקילות? כמובן. \( \left[a\right] \) כוללת את כל האיברים \( b\in G \) כך ש-\( b^{-1}a\in H \), כלומר כך שקיים \( h\in H \) עבורו \( b^{-1}a=h \), כלומר ש-\( b=ah^{-1} \). במילים אחרות, \( \left[a\right]=\left\{ ah\ |\ h\in H\right\} =aH \). קיבלנו שמחלקת השקילות של \( a \) היא בדיוק הקוסט השמאלי של \( H \) שנקבע על ידי \( a \). באופן כללי, כל מחלקות השקילות של היחס יהיו כל הקוסטים השמאליים של \( H \), מה שמסביר את הדמיון בין קוסטים ובין חלוקות - קוסטים הם פשוט מקרה פרטי של חלוקה. מעכשיו אני לא אטרח לכתוב \( \left[a\right] \) יותר - אני פשוט אכתוב \( aH \), כי כבר ברור על מה מדובר פה.

בשלב הזה אולי קופצת נורת אזהרה אצל חלקכם. אם כן, זה מצוין, כי יש הונאה כלשהי בדרך שבה הצגתי את הדברים, אבל לפני שנלך לשם בואו נראה דוגמא. וזו תהיה, איך לא, הדוגמא של \( \mathbb{Z} \). כאשר \( H=2\mathbb{Z} \), ראינו כבר שהקוסטים הם הזוגיים והאי-זוגיים. מהו יחס השקילות? הכתיב \( b^{-1}a\in H \) מתורגם במקרה הזה ל-\( a-b\in2\mathbb{Z} \), או בניסוח אחר - \( 2 \) מחלק את \( a-b \). זה בדיוק יחס השקילות שבדרך כלל מסומן במתמטיקה בתור \( a\equiv b\left(\text{mod }2\right) \). באופן דומה עבור \( n\mathbb{Z} \) נקבל את יחס השקילות מודולו \( n \). ומה חבורות המנה שאנחנו מקבלים? בפוסט הזה אציג את הפורמליזם המדויק ואוכיח זאת, אבל לא קשה לראות ש-\( \mathbb{Z}/n\mathbb{Z} \) זו בערך אותה חבורה כמו \( \mathbb{Z}_{n} \), עד כדי זה שאברי \( \mathbb{Z}_{n} \) הם מספרים טבעיים בתחום מסויים ואברי \( \mathbb{Z}/n\mathbb{Z} \) הם קבוצות של טבעיים.

זה מעניין, כי זה מצביע על כך שבחבורה הציקלית האינסופית היחידה, \( \mathbb{Z} \), מסתתרת האינפורמציה של כל החבורות הציקליות הסופיות - רק שהן מסתתרות לא בתור תת-חבורות של \( \mathbb{Z} \) (כל תת-החבורות של \( \mathbb{Z} \) הן ציקליות שנראות כמו \( \mathbb{Z} \)) אלא בתוך המנות של \( \mathbb{Z} \). זו אינטואיציה ראשונה לכך ש”להבין את המנות של החבורה עוזר להבין את המבנה שלה”.

אוקיי, אם הכל טוב, אז מה בעצם רע? נורית האזהרה שאמורה לקפוץ היא שאמרתי שמחלקות השקילות של היחס הן הקוסטים השמאליים של \( H \). למה דווקא השמאליים? מה זה חוסר הסימטריה הזה? מה עשיתי שהצדיק אותו? התשובה היא שהתחלתי עם המשוואה \( \left[a\right]=\left[b\right] \) והגעתי ממנה אל \( b^{-1}a\in H \). אבל באותה מידה יכלתי להגיע ממנה גם אל \( ab^{-1}\in H \) (תנסו!) ואז הייתי מגיע למסקנה שמחלקות השקילות הן הקוסטים הימניים של \( H \). בפרט, מחלקת השקילות של \( a \) הייתה גם הקוסט \( aH \) וגם הקוסט \( Ha \), דהיינו \( aH=Ha \). זה עלול להיראות בטעות כאילו הוכחתי שבחבורה כללית תמיד מתקיים ש-\( aH=Ha \) ולכן לא ברור למה מלכתחילה טרחתי להבדיל בין קוסטים ימניים לשמאליים. האמת היא שלא הוכחתי שום דבר כזה. התחלתי מלהניח שהפעולה על הקוסטים מגדירה חבורה וזו הנחה כבדה. מה שהראיתי פה הוא שהדרישה שיתקיים \( aH=Ha \) לכל \( a\in G \) היא תנאי הכרחי ש-\( H \) צריכה לקיים אם אנחנו רוצים שהפעולה של \( G \) תשרה מבנה של חבורה על אוסף הקוסטים של \( H \). כדי להשלים את הפוסט אני ארצה להוכיח שזה גם תנאי מספיק - כלומר, שאם \( H \) היא תת-חבורה עבורה מתקיים \( aH=Ha \) לכל \( a\in G \), אז הפעולה \( aH\cdot bH\triangleq\left(ab\right)H \) היא מוגדרת היטב ואוסף הקוסטים של \( H \) הוא חבורה ביחס אליה.

צריך להסביר את ה”מוגדר היטב” הזה. כפי שכבר ראינו, קוסט אפשר לייצג על ידי הרבה איברים. למשל, \( 2\mathbb{Z}+1=2\mathbb{Z}+3 \). אבל את הפעולה שלי על הקוסטים אני מגדיר על פי הנציגים. כלומר, אני אומר: רוצים לכפול שני קוסטים? נהדר. תבחרו באקראי שני איברים, אחד מכל קוסט, תכפלו את האיברים הללו וקחו את הקוסט של התוצאה. כדי שהפעולה הזו תהיה מוגדרת היטב אני צריך להראות שלא משנה אילו נציגים אני אבחר לכל קוסט, אני אקבל תמיד את אותו פלט. אחרת ה”פעולה” \( aH\cdot bH\triangleq\left(ab\right)H \) היא בכלל לא פונקציה אלא בולשיט.

למרבה המזל, ההוכחה פשוטה. בואו ניקח \( a_{1},a_{2} \) כך ש-\( a_{1}H=a_{2}H \) וניקח \( b_{1},b_{2} \) כך ש-\( b_{1}H=b_{2}H \). אני צריך להראות ש-\( \left(a_{1}b_{1}\right)H=\left(a_{2}b_{2}\right)H \) (כלומר, שלכל שתי בחירות אפשריות שונות של נציגים אני אקבל את אותה תוצאה, מה שמבטיח תוצאה זהה לכל בחירת נציגים). כבר ראינו קודם שבשביל להראות את זה, מספיק להראות ש-\( a_{2}b_{2}\in\left(a_{1}b_{1}\right)H \), כלומר שקיים \( h \) כך ש-\( a_{2}b_{2}=a_{1}b_{1}h \).

כעת, \( a_{1}H=a_{2}H \) פירושו שקיים \( h_{a} \) כך ש-\( a_{2}=a_{1}h_{a} \). בדומה, \( b_{1}H=b_{2}H \) פירושו שקיים \( h_{b} \) כך ש-\( b_{2}=b_{1}h_{b} \). אם כן:

\( a_{2}b_{2}=\left(a_{1}h_{a}\right)\left(b_{1}h_{b}\right)=a_{1}\left(h_{a}b_{1}\right)h_{b} \)

שימו לב ל-\( h_{a}b_{1} \) הזה! לו רק יכלנו להחליף את הסדר של שני אלו, היינו מקבלים \( a_{1}b_{1}\left(h_{a}h_{b}\right) \) והכל היה מסתדר! בחבורה אבלית אנחנו באמת יכולים להחליף והכל בסדר; אבל בחבורות לא אבליות זה לאו דווקא המצב. אז מה עושים? משתמשים בהנחה שלנו: \( bH=Hb \). מכיוון ש- \( h_{a}b_{1}\in Hb \) אז נקבל \( h_{a}b_{1}\in bH \), מה שאומר שקיים \( h^{\prime} \) כך ש-\( h_{a}b_{1}=b_{1}h^{\prime} \), ואז אנחנו מקבלים \( a_{2}b_{2}=a_{1}b_{1}\left(h^{\prime}h_{b}\right) \) והכל מסתדר. במילים אחרות, \( bH=Hb \) אומר ש-\( H \) מקיימת “סוג של קומוטטיביות” עם יתר החבורה: איבר כלשהו של החבורה לא מתחלף בכפל בהכרח עם אברי \( H \), אבל אפשר להחליף אותו בכפל עם איבר של \( H \) ב”מחיר” של שינוי האיבר הזה של \( H \) לאיבר אחר של \( H \). תת-חבורה \( H \) של \( G \) שהיא בעלת התכונה הזו, ש-\( aH=Ha \) לכל \( a\in G \), נקראת תת-חבורה נורמלית, ועוד רגע נראה עוד דרכים להגדיר אותה.

מה שהראינו היה שהפעולה \( aH\cdot bH\triangleq\left(ab\right)H \) על הקוסטים היא מוגדרת היטב. זה עדיין לא מוכיח שהקוסטים הם חבורה ביחס לפעולה הזו. יש לנו שלוש אקסיומות לטפל בהן. שתיים מהן, למרבה המזל, טריוויאליות ובעצם כבר ראינו אותן: \( eH=H \) היא בבירור איבר היחידה הכפלי (כי \( aH\cdot eH=\left(ae\right)H=aH \)). בדומה, לכל \( aH \) קיים הופכי: \( a^{-1}H \). מה שבעצם נותר הוא האסוציאטיביות. בניגוד למקרה של תת-חבורה, שם האסוציאטיביות “נורשת” מהפעולה המקורית, כאן בכל זאת צריך לעבור ולוודא בזהירות שאין בעיה:

\( aH\cdot\left(bH\cdot cH\right)=aH\cdot\left(bc\right)H=\left(a\left(bc\right)\right)H=\left(\left(ab\right)c\right)H=abH\cdot cH=\left(aH\cdot bH\right)\cdot cH \)

שום דבר מסובך, ובסופו של דבר האסוציאטיביות מתקבלת מכך שהפעולה ב-\( G \) המקורית הייתה אסוציאטיבית. זה מסיים את כל העסק הזה - אנחנו עכשיו רואים איך קוסטים צצים להם באופן טבעי כשמדברים על חבורות מנה, ומה אלו חבורות מנה בכלל, ויש לנו גם את המושג החדש של תת-חבורה נורמלית.

לסיום, אני רוצה לתת עוד אפיון למה זו תת-חבורה נורמלית, שהוא לרוב פופולרי קצת יותר (אבל לא צץ לי באופן “טבעי” פה, אז לא התחלתי ממנו). לצורך כך אני אציג מושג חדש: הצמדה. הצמדה זה משהו שהוא טריוויאלי בחבורות אבליות, ולכן עד כה לא ממש ראינו דוגמאות אליו כי התעסקתי בעיקר בחבורות אבליות. אם \( a \) הוא איבר כלשהו של \( G \) ואילו \( g \) הוא איבר אחר, אז ההצמדה של \( a \) על ידי \( g \) היא האיבר \( gag^{-1} \). זו פעולה שנראית מוזרה במבט ראשון, אבל סטודנטים למתמטיקה נתקלים בה כבר בקורס בסיסי באלגברה לינארית: אם \( A \) היא מטריצה שמייצגת טרנספורמציה לינארית בבסיס כלשהו, ו-\( P \) היא מטריצת מעבר אל הבסיס הזה מבסיס אחר, אז \( PAP^{-1} \) תהיה המטריצה שמייצגת את הטרנספורמציה ש-\( A \) מייצגת, רק בבסיס האחר. דוגמה אחרת היא עם פעולות של סיבוב ושיקוף (שאכן מהוות חבורה): תפתחו תוכנת ציור עם תמונה אהובה, תבצעו לתמונה שיקוף, אחר כך סיבוב ב-90 מעלות ימינה, אחר כך שוב שיקוף (שיקוף הוא ההופכי של עצמו). מה קרה? פעולות השיקוף לפני ואחרי גרמו לשינוי של טרנספורמציית הסיבוב.

בחבורה אבלית, \( gag^{-1}=agg^{-1}=a \) ולכן אין פה משהו מעניין, אבל בחבורות לא אבליות, כפי שראינו, בהחלט מדובר על פעולה לא טריוויאלית. ואם הגדרנו אותה על איברים בודדים, אפשר להגדיר אותה גם על חבורות: \( aHa^{-1}=\left\{ aha^{-1}\ |\ h\in H\right\} \). כעת, הגדרה שקולה של תת-חבורה נורמלית הוא בתור תת-חבורה \( H \) שמקיימת \( aHa^{-1}=H \) לכל \( a\in G \). למה זה נכון? אינטואיטיבית, כי בואו נכפול את המשוואה \( aHa^{-1}=H \) ב-\( a \) מצד ימין… אבל זו לא פורמליסטיקה. ברמה הפורמליסטית, אם \( aH=Ha \) אז \( aha^{-1}=h^{\prime}aa^{-1}=h^{\prime}\in H \) על פי הכלל שראינו קודם של “אפשר להחליף אם מחליפים” שזה ניסוח לא מבלבל בכלל. זה מוכיח ש-\( aHa^{-1}\subseteq H \). הכיוון הבודד הזה מספיק: אם \( aHa^{-1}\subseteq H \) לכל \( a \), אז אינטואיטיבית נכפול את המשוואה הזו משמאל ב-\( a^{-1} \) ומימין ב-\( a \) ונקבל \( H\subseteq a^{-1}Ha \) לכל \( a \), ובפרט עבור הצבה של \( a^{-1} \) במקום \( a \) נקבל \( H\subseteq aHa^{-1} \). פורמלית, אם לכל \( h\in H \) מתקיים ש-\( aha^{-1}\in H \) אז קיים \( h^{\prime} \) כך ש-\( aha^{-1}=h^{\prime} \), כלומר \( h=a^{-1}h^{\prime}a\in a^{-1}Ha \), כנדרש.

נשאר רק הכיוון השני, לפיו אם \( aHa^{-1}=H \) לכל \( a \) אז \( aH=Ha \) לכל \( a \). אפשר אפילו להסתפק בהנחה ש-\( aHa^{-1}\subseteq H \) כי כבר ראינו שהיא גוררת את השוויון. ניקח איבר של \( aH \), נאמר \( ah \). אז אנחנו יודעים ש-\( ah\cdot a^{-1}\in H \), כלומר \( ah\cdot a^{-1}=h^{\prime} \), כלמר \( ah=h^{\prime}a\in Ha \) וזה מה שרצינו. זה מסיים את האפיון הזה של תת-חבורות נורמליות, שלעתים קרובות הוא נוח יותר לעבודה מאפיון ה”קוסט שמאלי הוא קוסט ימני”.

בפוסט הבא - סוף סוף נתחיל לפרמל את נפנוף הידיים שלי של “היי תראו! החבורות הללו הן בדיוק אותו דבר בערך!”