המעשה המופלא בקבוע המסתורי 0x5f3759df (חלק א' - הקל)

למתמטיקאים יש את סיפורי המסתורין שלהם. המפורסם מביניהם הוא ככל הנראה הערה ששרבט פייר דה פרמה בשולי ספר ה”אריתמטיקה” של דיופנטוס שלו, שבה העיר שהכללה של טענה שהופיעה בספר היא שגויה תמיד וש”בידי הוכחה מופלאה למשפט אך שולי ספר זה צרים מלהכילה”. הערת השוליים הזו לא פורסמה על ידי פרמה בימי חייו והיא התגלתה רק כשנקראו הספרים שבעזבונו, ואז היה קצת מאוחר מדי לשאול את פרמה לאיזו הוכחה הוא התכוון. שום הוכחה דומה לא נמצאה בכתביו או התכתבויותיו, ובמשך למעלה מ-350 שנה המתמטיקאים ניסו להוכיח את המשפט שלו ללא הצלחה. גם כשנמצאה הוכחה, היא הייתה מודרנית ומורכבת ובוודאי לא “ההוכחה הנפלאה” של פרמה. מה הייתה ההוכחה המקורית? איך פרמה הגיע אליה? מתי ואיך הבין שאינה נכונה, אם בכלל? תעלומה.

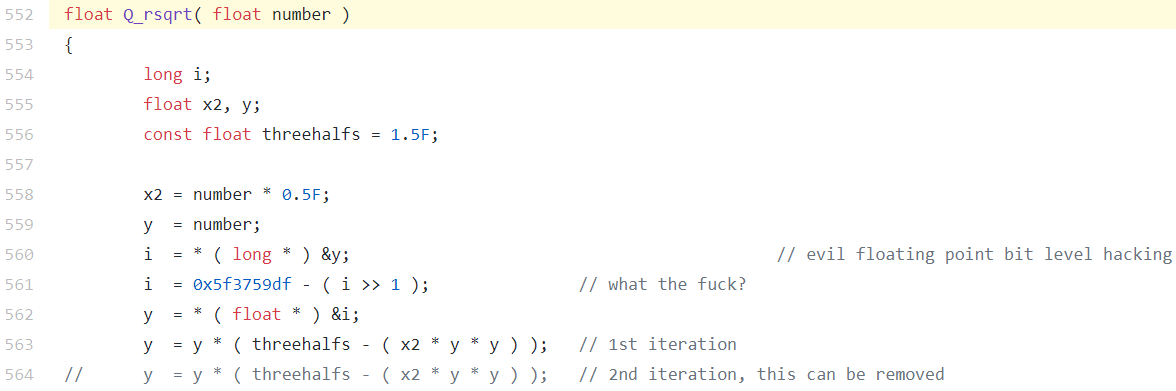
במדעי המחשב אין לנו תעלומות בנות מאות שנים - מדעי המחשב הם תחום צעיר יחסית. אבל היום אני רוצה לספר על תעלומה בת למעלה מעשור, שגם היא כנראה שלא תיפתר לעולם אבל היא מעניינת מספיק גם ככה - תעלומת המספר 0x5f3759df וקטע הקוד שבו הוא מופיע. קטע הקוד הזה נמצא, מכל המקומות בעולם, בקוד של משחק היריות מגוף ראשון Quake 3. הוא נתגלה בשנת 2005, כשקוד המשחק שוחרר לציבור הרחב. אפשר למצוא אותו כאן, והוא נראה ככה:

לא מבינים כלום? נהדר. בסופו של דבר נבין את הכל, וכנראה נחווה את אותה תחושה שגרמה למי שזה לא יהיה שכתב שם what the fuck? לכתוב זאת. אבל להבין את מלוא הפרטים של העניין הזה, זה חתיכת סיפור, ולכן אני אכתוב את הפוסט באופן הדרגתי מהקל אל הכבד, ואתם מוזמנים לנשור מתי שתתייאשו - הפוסט בנוי כך שכל חלק מסביר את הסיפור ברמת פירוט הולכת וגדלה ולא באמת חייבים להישאר עד הסוף כדי להבין מה הלך פה.

נתחיל עם קצת היסטוריה.

פרק ראשון, שבו המספר נזכר בערגה בראשית דרכו כגיימר ואנחנו לומדים איך לוחם בנאצים שינה את עולם משחקי המחשב לנצח

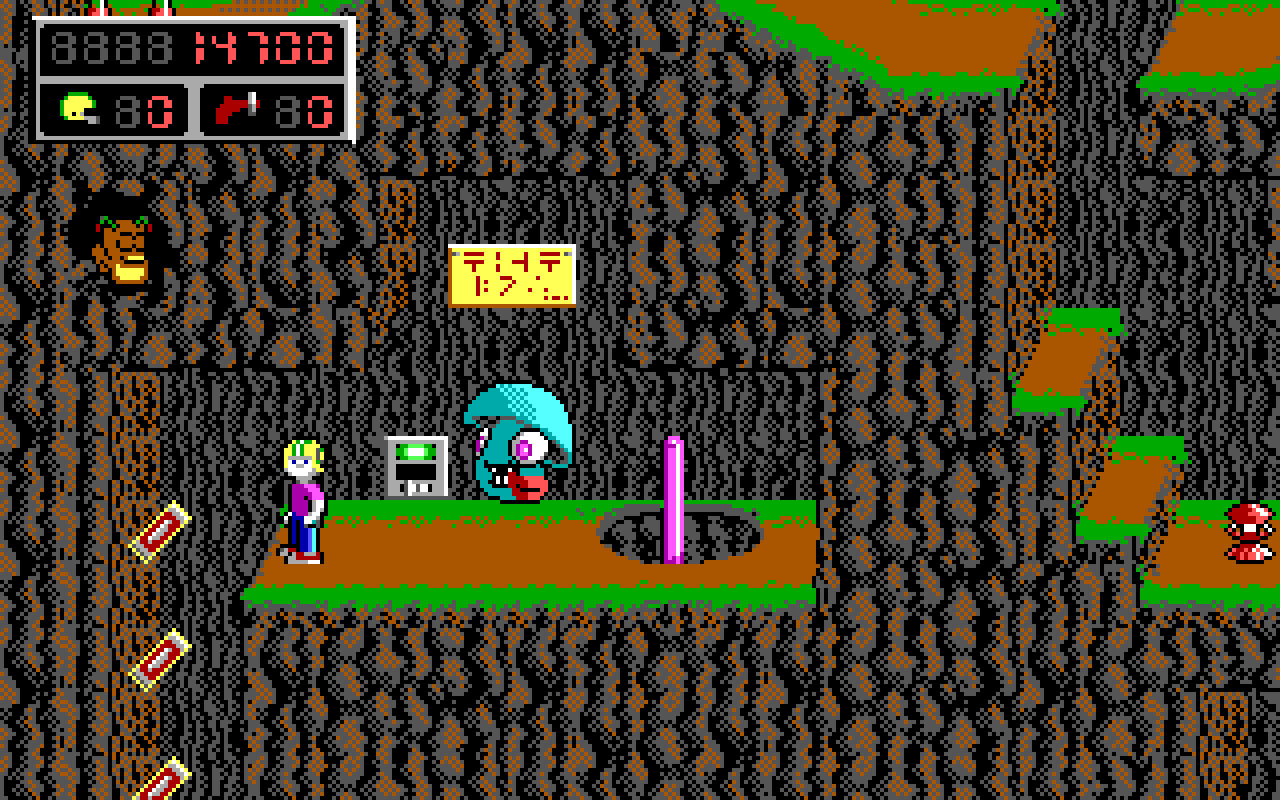
בואו נעבור לרגע לתחילת שנות התשעים. עולם המחשבים האישיים קיים כבר עשור או שניים, אבל עדיין מגשש את דרכו בזהירות. אז כמו עכשיו, היבט חשוב ביותר של משחקי המחשב הוא הגרפיקה שלהם - כמה טוב הם נראים. גרפיקה זה עניין מסובך. לא מספיק לדעת לצייר יפה, צריך גם לוודא שהמחשב יודע להציג את הציורים היפים מהר. כשמדובר על משחקי פעולה, זה קריטי לחלוטין שהמשחק ירוץ חלק ורציף תוך כדי שהוא נראה טוב. העבודה האמיתית כרגע נעשית מאחורי הקלעים: המתכנתים שצריכים לכתוב את המנוע של המשחק - הקוד שגורם למשחק לפעול, ובפרט הקוד שמאפשר את הצגת הגרפיקה - משתמשים בכל תעלול תכנות אפשרי כדי לגרד עוד קצת מהירות. הכל יחסית חלוצי. עדיין אין יותר מדי קוד קיים להתבסס עליו; אין נסיון מצטבר של עשרות שנים; אין מנועים קיימים בשוק שאפשר פשוט להשתמש בהם. בשנת 1991 מצטרפת לעולם הזה חברה חדשה - id Software. סדרת המשחקים הראשונה שהם מוציאים נקראת Commander Keen ועוסקת בהרפתקאותיו של ילד בן שמונה עם קסדת פוטבול ומקל פוגו ומלחמתו בחייזרים שמנסים להשמיד את כדור הארץ. ככה בערך זה נראה:

קין מתרחש בעולם דו-ממדי שבו אפשר לנוע ימינה, שמאלה, למעלה ולמטה, כשאנחנו מסתכלים על העניינים מהצד. למשטחים שעליהם הדמויות במשחק עומדים קוראים פלטפורמות ועל שמם משחקים כאלו נקראים משחקי פלטפורמות. אל תזלזלו במה שאתם רואים כאן. לזמנו הגרפיקה של המשחקים הללו הייתה טובה למדי (הסגנון הקרטוני הוא מכוון) והם אפילו היו חדשניים בתור משחקי פלטפורמות בכך שהתנועה בהם הייתה “חלקה” - דהיינו, במקום שהדמות תצא מהמסך שבו היא נמצאת ויעלה מסך אחר, המסך זז באופן רציף יחד עם הדמות של קין. לעשות את זה בזמנו על מחשב אישי (להבדיל מקונסולה כמו נינטנדו) לא היה טריוויאלי, והאחראי לתעלולי התכנות שאיפשרו את זה היה המתכנת הראשי של id software, ג’ון קרמק.

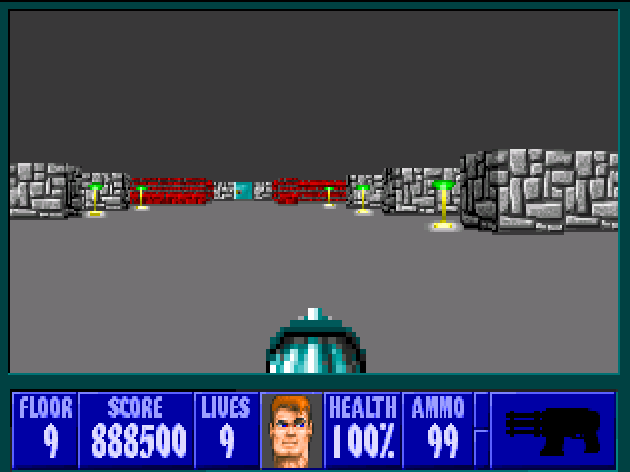
אחרי המנוע של קין קרמק עבר להתעסק עם אתגר אחר - מנוע גרפי תלת ממדי. במקום שהעולם יוצג מהצד, הוא מוצג מנקודת המבט של הדמות שאותה משחקים. המשחק המפורסם ביותר שהוציאה החברה עם המנוע הראשון שיצר קרמק נקרא Wolfenstein 3D. ככה זה נראה:

הגרפיקה פה שונה מהותית מזו של קומנדר קין. אצל קומנדר קין, הכל מצוייר ביד והמשחק פשוט מציג את הציורים הללו. לעומת זאת בוולפנשטיין התמונה שהשחקן רואה נוצרת בידי המחשב תוך כדי משחק: מישהו צייר את הטקסטורה של קיר ואפשר לראות שחוזרים עליה שוב ושוב, אבל אותה הטקסטורה מצויירת באופן קצת שונה בהתאם לקיר שרואים. אם הקיר רחוק יותר, רואים אותו קטן יותר; אם רואים אותו מהצד, הקיר מוצג בצורה אלכסונית. יש תאורה ויש הצללה (לכל הפחות, הקירות לפעמים בהירים ולפעמים כהים), וכדומה. במילים אחרות, המחשב לוקח תמונה של “איך קיר נראה” ומחשב איך בדיוק הקירות אמורים להיות מוצגים בהתבסס על המיקום הנוכחי של השחקן ושאר הפרטים שבזירה.

שימו לב שהמשחק עצמו הוא דו-ממדי: הדמות של השחקן יכולה לנוע רק ימינה, שמאלה, קדימה ואחורה (וכמובן, באלכסון שהוא שילוב של שניים מאלו). אין במשחק הזה אפשרות ללכת “למעלה” ו”למטה” בכלל. החשיבות היא בנקודת המבט של השחקן, לא במספר כיווני התנועה שלו. למשחק מסוג זה קוראים “משחק פעולה מגוף ראשון”. ומה עושים עם כל הגרפיקה הזו? ובכן, חסכתי את זה מכם בצילום המסך, אבל הרעיון במשחק (שמבוסס על משחקים משנות השמונים, נטולי גרפיקה תלת מימדית) הוא לשחק חייל אמריקאי יהודי שפולש לכל מני מעוזים נאציים במלחמת העולם השניה ומחסל את יושביהם, כולל היטלר עצמו מתישהו.

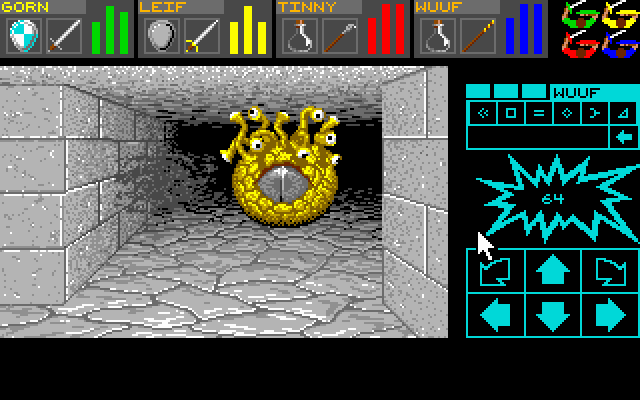
כמו עם קין, כך גם עם וולף 3D, המנוע שקרמק יצר בשביל המשחק חולל מהפכה זוטא. הגרפיקה שלו נראתה טוב מצד אחד, אבל מצד שני היא נוצרה מספיק מהר כדי שהמשחק ירוץ חלק, כפי שנדרש ממשחק יריות מהיר שכזה. השילוב של שני אלו היה מהפכה של ממש. בואו נראה דוגמאות למשחקים ישנים יותר כדי להבין מה השתנה. ראשית, הנה צילום מסך ממשחק מבוכים בשם Dungeon Master מ-1987:

כאן התמונה נראית תלת ממדית, אבל זו “רמאות” - מישהו צייר ביד את הכל - גם ציור של “קיר קרוב” וגם ציור של “קיר רחוק” וגם ציור של “קיר מהצד” וכדומה. המחיר של זה הוא שאי אפשר לנוע באופן חופשי - הדמות שאותה משחקים יכולה לבצע סיבובים של 90 מעלות ולנוע קדימה ואחורה משבצות שלמות בכל פעם וזהו. בוולף 3D התנועה היא חופשית וההרגשה של המשחק היא שונה לגמרי (הרבה יותר מתאימה למשחק יריות). והנה צילום מסך ממשחק הרפתקאות בשם Castle Master מ-1990:

כאן הגרפיקה היא תלת ממדית לגמרי. יש גם “למעלה” ו”למטה” ואפשר להסתכל אליהם ואפילו סוג של ללכת אליהם (למשל, אפשר ליפול). המחיר הוא שהגרפיקה הזו נראית ממש לא משהו והקצב של המשחק איטי (ה”קרבות” כוללים יצורים שעומדים או זזים בצורה לא רציפה ומנסים לפגוע בהם בלי שיש לתזוזה של השחקן שום ערך מוסף). המשחק עצמו די מהנה ומבוסס בעיקרו על פאזלים ועל שיטוט וחיפוש של דברים, אבל זה לא משחק פעולה.

מה שאני רוצה לומר לכם בסיפור הארוך הזה הוא כמה דברים שלטעמי הם קריטיים כדי להעריך את קטע הקוד המוזר שלעיל:

• גרפיקה היא דבר חשוב ביותר במשחקי מחשב.
• כשמדובר על משחקי פעולה תלת ממדיים אי אפשר להתפשר לא על איכות הגרפיקה ולא על מהירות המשחק. חייבים להיות יצירתיים ולהשיג את שניהם.
• בזמנו הדרך להשיג את הדברים הללו הייתה על ידי התחכמויות ברמת הקוד.
• ג'ון קרמק היה חתיכת פורץ דרך רציני למרות שבקושי מכירים את השם שלו מחוץ לחוגים הרלוונטיים.

במקרה הספציפי של וולף 3D ההשקעה השתלמה. היה כאן שילוב של המנוע הגרפי, העיצוב הסגנוני של המשחק והאופן החכם שבו הוא הופץ (הפצה חינמית של החלק הראשון שלו, מודל שעבד לא רע גם עם קומנדר קין) והמשחק היה הצלחה גדולה. id software ראתה כי טוב והמשיכה בכיוון של משחקי יריות מגוף ראשון. ג’ון קרמק יצר מנוע תלת ממדי חדש ומתוחכם בהרבה מזה של וולף 3D, ועל בסיסו עוצב אחד ממשחקי המחשב החשובים ביותר בהיסטוריה - Doom. בבסיסו, דום הוא כמו וולף 3D רק עם שדים במקום נאצים והגיהנום במקום טירה. לאחר ההצלחה הגדולה של דום (וההמשך שלו) עברה החברה לסדרה חדשה של משחקי יריות מתלת מימד - Quake. שבהם העלילה היא… אה… טוב, למי אכפת בכלל. ב-1999 יצא Quake 3 שבו כל הקונספט הזה של עלילה די נזנח לטובת קרבות מרובי משתתפים. בשלב הזה הגרפיקה כבר נראתה הרבה, הרבה יותר טוב והייתה תלת מימדית באופן מלא:

מה השתנה בשנים שחלפו שאיפשר גרפיקה יותר טובה? ראשית, המחשבים היו יותר חזקים. שנית, הם התחילו להשתמש ברכיבי חומרה ייעודיים להצגת גרפיקה (מה שנקרא בשעתו “מאיץ גרפי”). אבל תכנות חכם של המנוע עדיין היה אספקט קריטי, והמנוע שמאחורי Quake 3 היה מוצלח מאוד. לכן כשג’ון קרמק הודיע בשנת 2005 שקוד המקור המלא של המנוע ישוחרר לרשת לטובת כל מי שבא לו לקרוא אותו (בינתיים כבר פותח המנוע הבא בתור) הייתה שמחה גדולה. ואנשים רצו לקרוא את הקוד. ואז התגלה בו קטע הקוד הקצרצר שבו אנחנו עוסקים כאן.

עוד מעט אסביר מה בדיוק הקוד הזה עושה, אבל בקצרה: הוא עוזר, בצורה חכמה מאוד, לעשות גרפיקה יפה ומהירה וכבר הסכמנו שזה חשוב. השאלה המעניינת יותר היא מי כתב אותו, ומתי. מן הסתם החשוד המיידי היה ג’ון קרמק עצמו, אבל כששאלו אותו הוא אמר בפשטות שלא, זה לא הוא, אולי זה הברנש האחר ההוא… אבל גם הברנש האחר ההוא הכחיש כל קשר. אפשר לקרוא עוד על החיפוש כאן. השורה התחתונה - לאף אחד אין מושג מי כתב את הקוד הזה. כנראה שהוא עתיק בהרבה מאשר המנוע של Quake 3 ולא ברור איך בדיוק התגלגל לשם. פשוט תעלומה. זה לא לגמרי מפתיע - ככה זה עם קוד מחשב רציני, יש דברים ש”מתגלגלים” פנימה בלי שלאף אחד יהיה מושג אחר כך מה הולך כאן. אבל הקוד הזה הוא דוגמה יפה במיוחד לכך. בעיקר כי הוא עושה את מה שהוא אמור לעשות בצורה יעילה עד להפתיע. זה קצת מזכיר את הסיפור של הסנדלר הכושל שגמדים באו בלילה ועשו את העבודה שלו בשבילו, ובצורה טובה בהרבה.

פרק שני, שבו אנחנו לומדים לקרוא קוד שנראה כמו ג'יבריש ומבינים הכל אבל לא מבינים שום דבר

לפני שנתחיל לצלול לקוד, בואו נבהיר מה הוא עושה: זו פונקציה שלוקחת מספר \( x \) ומחשבת את \( \frac{1}{\sqrt{x}} \), כלומר את ההופכי של השורש של \( x \). זה הכל. למה זה חשוב לגרפיקה? אסביר זאת בהמשך, אבל בשורת מחץ אחת: כי ככה מנרמלים וקטורים. שאלה אחרת היא למה לעשות את זה ככה ולא לבנות כמו בני אדם שפויים פונקציה שלוקחת את \( x \) ומחשבת את \( \sqrt{x} \) ואחר כך אפשר לעשות פעולת חילוק רגילה ולחשב את \( \frac{1}{\sqrt{x}} \) כמו בני תרבות. התשובה היא יעילות. יעילות היא מילת המפתח בכל מה שאנחנו עושים פה. פעולת חילוק היא בדרך כלל פעולה יקרה לביצוע יחסית; אם אפשר להימנע ממנה, למה לא. להבדיל, פעולת כפל היא פחות יקרה, אז אם יש לנו פונקציה יעילה מאוד שמחשבת את \( \frac{1}{\sqrt{x}} \) יחסית קל לחשב את \( \sqrt{x} \): פשוט מחשבים את המכפלה \( x\cdot\frac{1}{\sqrt{x}} \). המחיר של קודם כל לחשב ביעילות את \( \frac{1}{\sqrt{x}} \) ואז לבצע את ההכפלה יהיה זול יותר מאשר המחיר של קודם לחשב את \( \sqrt{x} \) ואז לחשב את המנה \( \frac{1}{\sqrt{x}} \).

קחו מבט נוסף על הקוד, עכשיו כשאתם יודעים מה הוא אמור לעשות. האם אתם מרגישים קצת מוזר? אני מרגיש מאוד מוזר. חישוב שורש… זה משהו שאמור להיות מסובך, לא? איך אפשר שקוד יבצע גם חישוב שורש וגם הופכי שלו ביחד בכל כך מעט שורות קוד, ויעשה את זה מהיר ומדויק? משהו פה מרגיש כאילו הוא לא מסתדר. אבל הכל מסתדר - זה עובד, וזה עובד מאוד יפה.

בואו נסביר את הקוד שורה שורה, עבור מי שלא מכיר שפות תכנות. אין כאן שום דבר שמעבר ליכולת ההבנה שלכם - זה קוד מאוד פשוט. רק טיפה טרמינולוגיה קודם: כשאני מדבר על “מספר ממשי” אני מתכוון לכל מספר שאנחנו יודעים לכתוב עם ייצוג עשרוני, למשל 3 או 3.141 או 0.333 וכדומה. ליתר דיוק, אני מתכוון רק לאלו מתוכם שאנחנו יודעים לייצג במחשב, אבל מי אלו בדיוק נראה רק בהמשך. באופן דומה, “מספר שלם” הוא מספר שאין לו כלום אחרי הנקודה העשרונית. 3 הוא שלם ו-3.1 או 0.3 הם לא שלמים. גם על השלמים יש הגבלה, שלא אתאר כרגע, לגבי מי מהם יכול להיות מיוצג במחשב.

float Q_rsqrt( float number )

השורה הראשונה הזו אומרת “שלום בוקר טוב אני פונקציה ושמי הוא Q_rsqrt (אני מנחש ש-rsqrt זה קיצור של reciprocal square root - ההופכי של שורש ריבועי), אני מקבלת קלט בשם number שהוא מספר ממשי ומחזירה פלט שגם הוא מספר ממשי”. מה שאולי לא ברור לכם הוא למה משתמשים במילה float כדי לתאר מספר ממשי; הסיבה לכך היא שבשפת C, מספרים ממשיים מיוצגים על ידי שיטת ייצוג שנקראת נקודה צפה ואתאר בהמשך הפוסט. אתם לא באמת צריכים להבין אותה בשלב הזה.

שלוש השורות הבאות מגדירות משתנים וקבועים שבהם ישתמשו בהמשך הפונקציה:

long i;
float x2, y;
const float threehalfs = 1.5F;

המשתנים x2,y שניהם מספרים ממשיים. לעומת זאת i הוא מספר שלם. זה חשוב כי מספרים שלמים מיוצגים בצורה שונה מאשר מספרים ממשיים כלליים. המילה long נובעת מכך שיש שיטות שונות לייצג מספרים שלמים ב-C שנבדלות בגודל המקסימלי של המספרים שאפשר לייצג. שם מקובל למספר שלם הוא int, קיצור של integer; השם long בא לומר שהמספר השלם הולך להיות גדול יחסית - לכל הפחות בתחום מספרים סביב 0 שגודלו \( 2^{32} \), ואולי גם יותר (לא ניכנס פה לדקויות של הגדרות טיפוסים ב-C, זו זוועה שאין כמוה).

השורה האחרונה מגדירה קבוע: משתנה שערכו נקבע מראש ולא ישתנה אחר כך. במקרה הנוכחי, threehalfs מוגדר להיות בדיוק מה ששמו מרמז: המספר 1.5 כאשר הייצוג שלו הוא על ידי float (זה ה-F שבסוף). למה צריך את הקבוע הזה? בהמשך, כשנראה את החישובים שעומדים מאחורי הפונקציה הזו, נראה שהוא אכן צץ מעצמו.

שתי השורות הבאות מאתחלות את המשתנים שהוגדרו קודם:

x2 = number * 0.5F;
y = number;

כלומר, \( y \) הוא כרגע בדיוק המספר שקיבלנו בתור קלט, ו-\( x2 \) הוא חצי ממנו. למה צריך את זה, נראה אחר כך.

שלוש השורות הבאות הן ללא ספק החלק הכי לא ברור בכל הקוד:

i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;

ראשית, הטקסט האנגלי שמופיע אחרי זוג הלוכסנים בסוף שתי השורות הראשונות הוא הערה, כלומר משהו שלא רץ בפועל אלא קיים שם למען הדורות הבאים שיקראו את הקוד. אני מנחש שמי שהוסיף את ההערות הללו לא היה המתכנת המקורי אלא מישהו שניסה להבין מה בעצם הוא עשה שם, וכפי שניתן לראות, השורה האמצעית די בלבלה אותו… כל שלוש השורות הללו הן לחלוטין בלתי קריאות למי שלא מכיר C, אבל קל להסביר את ה”בערך” של מה שהן עושות: השורה הראשונה אומרת “קח את המספר הממשי y ותתייחס אליו לרגע בתור מספר שלם, ואת זה תציב ב-i’’. השורה האחרונה אומרת “קח את המספר השלם i ותתייחס אליו לרגע בתור מספר ממשי ואת זה תציב ב-y”. מפתה לומר שמתבצעת פה המרה ממספר ממשי למספר שלם, וההפך. אבל זה ממש לא מה שקורה פה. המרה היא תהליך מתוחכם שבו מתבצעת מניפולציה על המספר, למשל \( 3.7 \) יומר ל-\( 3 \) כאשר מבצעים המרה. לא. מה שקורה פה הוא יותר מוזר: אנחנו לוקחים את האופן שבו המספר הממשי מיוצג במחשב ומתייחסים לדבר הזה בתור ייצוג במחשב של מספר שלם. זה תעלול מוזר מאוד כי שיטות הייצוג של שני סוגי המספרים הללו הן שונות בתכלית. אפרט על זה בהמשך.

ואז מגיעה השורה האמצעית. דווקא אותה די קל להבין, אבל צריך להכיר את הסימונים. ראשית, הקבוע המסתורי 0x5f3759df. הקבוע הזה הוא בסך הכל דרך ייצוג מקובלת למספר השלם 1597463007, כאשר כותבים אותו בבסיס הקסדצימלי, כלומר בסיס ספירה שבו יש לנו 16 ספרות. ה-0x בהתחלה הוא האופן הסטנדרטי שבו מודיעים לשפת C “הנה עכשיו אני מביא לך מספר בבסיס 16 ולא בבסיס 10 כמו בדרך כלל” וה-d,f הללו שנמצאים שם הם פשוט הספרות עבור 13 ו-15.

קצת יותר מסתורי ה-i » 1 הזה. אני אסביר בהמשך למה בדיוק משתמשים בסימון הזה, אבל המשמעות שלו פשוטה - זו חלוקה ב-2. אם כן, כל מה שהשורה הקסומה הזו עושה הוא לקחת את הקבוע 0x5f3759df ולהפחית ממנו את “הקלט של הפונקציה שלנו כאשר הוא מתפרש איכשהו בתור מספר שלם ומחולק ב-2”.

למה? למה עושים דבר מוזר כזה? בשביל מה?

התשובה היא שהשורות הללו נותנות לנו קירוב לערך של \( \frac{1}{\sqrt{x}} \). הקירוב הזה רחוק מלהיות מושלם, אבל הוא טוב בצורה מפתיעה. כדי לשפר את הקירוב הזה עוד יותר מגיעות השורות האחרונות בקוד:

y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed

השורות הללו מבצעות שתיהן בדיוק את אותו חישוב: \( y\leftarrow y\left(\frac{3}{2}-x_{2}y^{2}\right) \). החישוב הזה הוא מימוש למקרה הספציפי שלנו של שיטת קירוב שנקראת שיטת ניוטון-רפסון ואתאר בהמשך. הרעיון בשיטת ניוטון-רפסון הוא שזו שיטה איטרטיבית: כשרוצים לחשב איתה משהו, מתחילים עם קירוב כלשהו שלו, ואז מפעילים על הקירוב הזה חישוב שמשפר אותו, שוב, ושוב, ושוב. אחרי כל הפעלה של ניוטון-רפסון הקירוב שלנו משתפר עד שבסוף הוא “קרוב מספיק לצרכים שלנו” ואפשר להפסיק. השיטה הזו פועלת די מהר - על פי רוב לא צריך יותר משלוש-ארבע איטרציות שלה כדי להגיע לקירוב מצויין, אבל הקוד הנוכחי שלנו שאפתני יותר - הוא טוען ששתי איטרציות יספיקו. רגע, לא, הוא טוען אפילו יותר מזה! הוא טוען שאיטרציה אחת תספיק! השורה השניה, אם תסתכלו טוב, כולה הערה: היא מתחילה בשני לוכסנים. כנראה שמה שקרה הוא שבמקור השורה השניה הייתה חלק מהקוד שרץ בפועל, ומתישהו המתכנת הרלוונטי אמר “אוקיי בואו נסיר אותה ונראה אם משהו מעניין השתנה” והתוצאה הייתה שמצד אחד הקוד רץ מהר יותר ומצד שני לא נראה שום נזק בעל חשיבות, ולכן הוחלט לוותר על השורה השניה לגמרי.

זה אומר שעיקר העבודה של הפונקציה מתבצעת בשלוש השורות שראינו קודם, של “הקירוב ההתחלתי”. איכשהו מתבצע שם קסם שכזה שאחריו מספיקה הפעלה בודדת של ניוטון-רפסון כדי שכל העסק יעבוד טוב.

את שני החלקים הללו של הקוד אפשר להבין באופן בלתי תלוי זה בזה. לכן אתחיל דווקא מהתיאור של ניוטון-רפסון, שהיא שיטה פשוטה יחסית, ואחר כך אעבור לדבר על הטירוף של שורות הקירוב ההתחלתי.

פרק שלישי, ובו סקירה מהירה של השיטה המהירה של ניוטון-רפסון

ניוטון-רפסון היא שיטת קירוב. אנחנו רוצים לחשב שורש של מספר כלשהו, למשל \( \sqrt{2} \)? בשיטת הייצוג העשרוני הרגילה שלנו יש למספר הזה אינסוף ספרות אחרי הנקודה, והן לא מחזוריות. אז נצטרך להפסיק מתישהו. נאמר, אחרי ארבע ספרות זה מספיק לנו? במקרה הזה כל מספר שמתחיל ב-\( 1.4142 \) יהיה מספיק טוב לנו. מה שניוטון-רפסון עושה הוא לקחת קירוב התחלתי למספר שאנחנו רוצים לחשב, ואז לשפר את הקירוב הזה שוב, ושוב, ושוב. בכל שיפור אנחנו מרוויחים כמה ספרות מדויקות חדשות אחרי הנקודה. כשאנחנו רואים ש”התקבעו” לנו מספיק ספרות, אנחנו עוצרים.

איך הקסם הזה קורה? מעשית, ניוטון-רפסון מנוסח כך: יש לנו פונקציה \( f:\mathbb{R}\to\mathbb{R} \) ואנחנו רוצים למצוא \( x \) כך ש-\( f\left(x\right)=0 \), מה שנקרא, למצוא נקודת חיתוך של \( f \) עם ציר \( x \). למשל, עבור \( \sqrt{2} \) אנחנו נסתכל על הפונקציה \( f\left(x\right)=x^{2}-2 \), שאותה קל לנו לחשב באמצעות פעולות בסיסיות בלבד (להבדיל נאמר מהפונקציה \( f\left(x\right)=x-\sqrt{2} \) שגם אצלה נקודת החיתוך היא ב-\( x=\sqrt{2} \) אבל אנחנו לא יודעים איך לחשב אותה). הכלי שבאמצעותו אנחנו ניגשים לבעיה הזו הוא הנגזרת של \( f \). הרעיון האינטואיטיבי של נגזרת הוא שהיא מאפשרת לנו לקרב את \( f \) בכל נקודה על ידי קו ישר - מה שנקרא קירוב לינארי. כלומר, למצוא קו ישר ש”באופן מקומי” מתנהג כמו \( f \). ההנחה של ניוטון היא שאם \( f \) היא נחמדה מספיק ולא משתוללת, ואם אנחנו כבר עכשיו די קרובים לנקודת החיתוך של \( f \) עם ציר \( x \), אז נקודת החיתוך של הקירוב הלינארי של \( f \) עם ציר \( x \) תהיה אפילו עוד יותר קרובה לנקודת החיתוך האמיתית מאשר המיקום הנוכחי שלנו.

מבחינה חישובית קל מאוד להגיע לנוסחה המדויקת של השיטה - כל כך קל, שאפשר להראות את זה כבר בתיכון לתלמידים שלמדו חדו”א וגאומטריה אנליטית, ואף פעם לא הבנתי למה לא לעשות את זה. הרעיון הוא כזה: נניח שאנחנו כרגע בנקודה \( x_{n} \), ואנחנו רוצים למצוא קירוב טוב יותר, \( x_{n+1} \). הנגזרת בנקודה \( x_{n} \) היא הערך \( f^{\prime}\left(x_{n}\right) \). המספר הזה הוא השיפוע של הקו הישר שמקרב את \( f \) בנקודה \( x_{n} \). עכשיו, בגאומטריה אנליטית אנחנו לומדים איך למצוא את השיפוע של הקו הישר שעובר דרך שתי נקודות נתונות. אם הנקודות הן \( \left(x_{1},y_{1}\right) \) ו-\( \left(x_{2},y_{2}\right) \) אז השיפוע הוא \( \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \) (אלא אם \( x_{1}=x_{2} \) ואז הסיפור קצת יותר מסובך). עכשיו, במקרה שלנו אנחנו יודעים על אחת משתי הנקודות - הנקודה \( \left(x_{n},f\left(x_{n}\right)\right) \) שבה אנו מחשבים את הקירוב הלינארי. הנקודה השניה שמעניינת אותנו היא נקודת החיתוך של הישר עם ציר \( x \), ומה שאנחנו מחפשים הוא את קואורדינטת ה-\( x \) שלה, מה שאני קורא לו \( x_{n+1} \). כלומר, הנקודה השניה היא \( \left(x_{n+1},0\right) \). נציב את שתי הנקודות הללו ואת הערך של השיפוע במשוואה שתיארתי קודם, ונקבל:

\( \frac{f\left(x_{n}\right)-0}{x_{n}-x_{n+1}}=f^{\prime}\left(x_{n}\right) \)

כלומר, לאחר העברת אגפים נקבל

\( x_{n+1}=x_{n}-\frac{f\left(x_{n}\right)}{f^{\prime}\left(x_{n}\right)} \)

למשל, בדוגמא של \( f\left(x\right)=x^{2}-2 \) שלנו נקבל ש-\( f^{\prime}\left(x\right)=2x \) ולכן הנוסחה שניוטון-רפסון נותן לנו היא

\( x_{n+1}=x_{n}-\frac{x_{n}^{2}-2}{2x_{n}}=\frac{1}{2}\left(x_{n}+\frac{2}{x_{n}}\right) \)

ואם אנחנו רוצים למצוא קירוב ל-\( \sqrt{a} \) עבור \( a \) כללי, הנוסחה תהיה

\( x_{n+1}=\frac{1}{2}\left(x_{n}+\frac{a}{x_{n}}\right) \)

במילים אחרות, ניוטון-רפסון אומר לנו במקרה הזה “כדאי לכם להסתכל על הממוצע החשבוני בין הקירוב הנוכחי שלכם לבין המספר ש’משלים אותו’ על ידי כפל ל-\( a \)”. תדמיינו שהמטרה שלנו היא למצוא ריבוע ששטחו \( a \). אנחנו מתחילים עם מלבן, ואז לוקחים את הממוצע בין אורכי הצלע הקצרה והארוכה, ובונים מלבן חדש שהמספר שקיבלנו הוא אורך אחת מצלעותיו ואת השניה אנחנו בונים כדי שהשטח יהיה שוב פעם \( a \). סדרת המלבנים שלנו תלך ותתקרב לריבוע.

בשביל השיטה הזו למציאת שורש אין צורך בניוטון - היא ככל הנראה הייתה ידועה כבר לבבלים ונמצאת בכתביו של המתמטיקאי הרון מאלכסנדריה. אבל זה נחמד מאוד שהיא מתקבלת מניוטון בתור מקרה פרטי פשוט.

עכשיו, משהבנו בערך מה הולך פה, בואו ניישם את ניוטון עבור המקרה שלנו: אנחנו רוצים לחשב לא את \( \sqrt{a} \) אלא את \( \frac{1}{\sqrt{a}} \), שהוא קצת יותר מסובך. במקרה הזה, נבחר בתור הפונקציה שלנו את \( f\left(x\right)=\frac{1}{x^{2}}-a \), ונקבל \( f^{\prime}\left(x\right)=-\frac{2}{x^{3}} \). לכן:

\( x_{n+1}=x_{n}+\frac{x_{n}^{3}}{2}\left(\frac{1}{x_{n}^{2}}-a\right)=x_{n}+\frac{x_{n}}{2}-\frac{x_{n}^{3}}{2}a=x_{n}\left(\frac{3}{2}-\frac{a}{2}x_{n}^{2}\right) \)

האם הנוסחה האחרונה נראית לכם מוכרת? בואו נסתכל שוב בשורות הרלוונטיות בקוד:

const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration

השורה האחרונה פה היא בדיוק הנוסחה שהגענו אליה כרגע. עד לרמת ה-\( \frac{3}{2} \) שנכתב במפורש בקוד והשימוש ב-\( x2 \) בתור \( \frac{a}{2} \). ומה עם \( y \)? כזכור, הערך שלו הוא הקירוב ההתחלתי שמחושב בצורה מתוחכמת למדי קודם. זה הצעד הבא שנצטרך להבין; אני חושב שאת החלק של הניוטון-רפסון אנחנו מבינים מושלם עכשיו. בחלק הבא של הפוסט נתחיל להשתגע באמת.