מה הקשר בין חוגי פולינומים לאימות חומרה?

ביקשו ממני לכתוב פוסט שיתן שימוש כלשהו למה שדיברתי עליו על חוגים במדעי המחשב. ובכן, לא הצלחתי לחשוב על משהו מוחץ ממש. התחום השימושי ביותר הוא ככל הנראה תורת השדות, בפרט שדות סופיים, אבל אני לא מחשיב את התחום הזה כחלק מתורת החוגים אלא כתחום העומד בפני עצמו. האם אני יכול לשלוף מהשרוול דוגמא שמשתמשת רק בדברים שראינו עד כה - וספציפית, אידאלים?

ואז קפץ לי לראש מאמר מ-2017 שקראתי לא מזמן (“Column-Wise Verification of Multipliers Using Computer Algebra” של Ritirc, Biere, Kauers) ונותן הצצה לשימוש בחוגים שהוא אולי לא מתבקש לגמרי במבט ראשון - שימוש בתחום של אימות חומרה. אני לא טוען שמה שמוצג במאמר הזה הוא הדבר הכי טוב שאפשר לעשות עם חוגים באימות חומרה (וממילא רוב הטכניקות לאימות חומרה שאני מכיר לא משתמשות בכלל בחוגים) אבל המאמר הזה נותן הקדמה טובה ל”איך עושים את זה” שהיא מה שאני רוצה לדבר עליו פה, ולא על התוכן היותר ספציפי וטכני שלו.

הבעיה הבסיסית של אימות חומרה היא זו: נתון לנו מעגל לוגי כלשהו עם קלט ופלט, שאמור לחשב פונקציה מסויימת. אנחנו רוצים לוודא שהוא אכן מחשב אותה. מה זה “מעגל לוגי”? אפשר לחשוב עליו בתור גרף מכוון וחסר מעגלים שבו כל צומת מייצג ביט בודד (0 או 1). הצמתים שאין להם כניסות הם הקלטים, הצמתים שאין להם יציאות הם הפלטים, ולכל צומת שאיננו קלט מתאימה פעולה לוגית כלשהי. למשל, פעולת AND שמחזירה 1 רק אם שני הקלטים שלה הם בעצמם 1, ואחרת מחזירה 0, או פעולת NOT שמקבלת קלט בודד ומחזירה 1 אם הקלט היה 0 ואחרת מחזירה 0. הרעיון הוא זה: תציבו ערכים באופן שרירותי בקלטים, תבצעו את החישוב שמתאים לצמתים שאינם קלט ותראו איזה פלט תקבלו בסוף.

נשמע פשוט? ובכן, צריך לזכור שבמעגלים אמיתיים יכולים להיות עשרות אלפי קלטים ומיליוני צמתים פנימיים. במעגלים אמיתיים הסיטואציה גם מסובכת יותר כי החישוב מתבצע ב”סיבובים” כשהפלטים של כל סיבוב יכולים להיות חלק מהקלטים של הסיבוב הבא, וסוג השאלות שנשאל הוא בסגנון “האם אחרי עשרים סיבובים הפלט הזה-והזה עשוי לצאת 0?”. מצד שני, הבעיה היא באמת פשוטה יחסית לניסוח; באימות תוכנה, למשל, הסיטואציה הרבה יותר מורכבת.

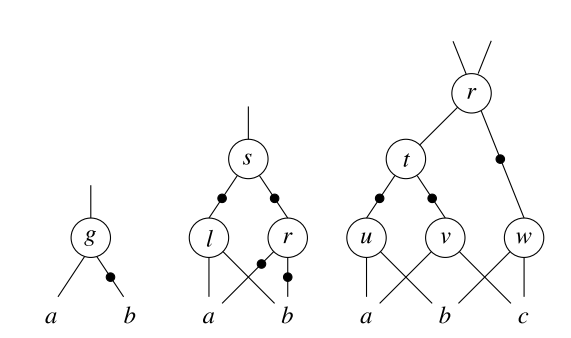
צורה מקובלת מאוד בתחום לתאר מעגל היא באמצעות שערי AND ו-NOT בלבד, ואפילו בצורה מפושטת: בגרף מציירים רק שערי AND, ואילו שערי ה-NOT מופיעים בתור סימונים שיכולים להופיע על הקשתות שנכנסות לשערי ה-AND. הנה דוגמא מתוך המאמר:

במעגל השמאלי ביותר הפונקציה שמחושבת היא \( g=a\wedge\neg b \). באמצעי החישוב כבר כולל שלושה צמתי ביניים:

• \( l=a\wedge b \)
• \( r=\neg a\wedge\neg b \)
• \( s=\neg l\wedge\neg r \)

ואם חושבים על זה לרגע, רואים שהפונקציה שמחושבת פה היא \( s=\left(a\ne b\right) \) (כלומר, \( s \) מקבלת 1 אם ורק אם \( a,b \) שונים זה מזה). עכשיו בואו תעשו כמוני עבור המעגל הימני ביותר ותגלו איזו פונקציה הוא מחשב כי בחיי שאין לי כוח לבדוק בעצמי.

המבנה הזה של גרף, שנקרא AIG (קיצור של And-Inverter Graph) הוא מאוד מועיל בתור ייצוג ביניים שמופק ממעגל חומרה “אמיתי” (כזה שנכתב ב-VHDL, למשל) ואפשר לבצע בו אופטימיזציות ואז לשלוח אותו הלאה, לאלגוריתם שמבצע אימות חומרה בפועל. אבל האלגוריתמים הללו על פי רוב משתמשים בייצוגים שונים ויותר מתאימים להם של הפונקציה שהגרף מחשב. בעבר הייצוג הפופולרי היה סוג של גרף מאופטמז שנקרא BDD, אבל לא אציג כאן. הייצוג הפופולרי ביותר בימינו הוא נוסחת CNF שמקודדת את המעגל - למשל, המעגל השמאלי ניתן לתיאור על ידי הנוסחה \( \left(\neg a\vee b\vee g\right)\wedge\left(a\vee\neg c\right)\wedge\left(\neg b\vee\neg c\right) \) שמקבלת 1 אם ורק אם מתקיים \( g=a\wedge\neg b \). בצורה הזו, השמה מספקת לנוסחת ה-CNF מתאימה לחישוב חוקי במעגל. אבל אם לא הבנתם כלום מזה, לא חשוב - אני לא הולך לדבר על שיטת הייצוג הזו מעבר לאזכור שלה.

מה שאנחנו רוצים לדבר עליו הוא ייצוג של המעגל בעזרת פולינומים. הרעיון הוא כזה: נניח ש-\( g,a,b \) הם כולם משתנים (מה שבדרך כלל אנחנו משתמשים עבורו ב-\( x,y,z \)). הנה פולינום לדוגמא שמשתמש במשתנים הללו: \( p\left(g,a,b\right)=a\left(1-b\right)-g \). לפולינום הזה יש את התכונה הבאה: אם נציב למשתנים ערכים שהם או 0 או 1, אז הפולינום יתאפס רק על ערכים שבהם \( g=a\wedge\neg b \). כלומר, השורשים של הפולינום מתאימים לחישוב חוקי של \( g=a\wedge\neg b \). דרך אחת לומר את זה היא לומר שהקשר \( g=a\wedge\neg b \) ניתן לתיאור באמצעות זהות פולינומית.

הנה האופן שבו אפשר להמיר את כל השערים הבסיסיים שאפשר לצפות לפגוש במעגל בוליאני בזהויות פולינומיות מתאימות:

• את \( g=\neg a \) אפשר לתאר עם \( p\left(g,a\right)=\left(1-a\right)-g \)
• את \( g=a\wedge b \) אפשר לתאר עם \( p\left(g,a,b\right)=ab-g \)
• את \( g=a\vee b \) אפשר לתאר עם \( p\left(g,a,b\right)=ab-\left(a+b\right)+g \) (אפשר להגיע לזה בקלות משני הקודמים בעזרת כללי דה-מורגן).
• את \( g=a\oplus b \) אפשר לתאר עם \( p\left(g,a,b\right)=2ab-\left(a+b\right)+g \)

באופן כללי, “זהות פולינומית” במעגל \( C \) היא פולינום \( p\left(x_{1},\dots,x_{n}\right) \) שהמשתנים שלו מתאימים לצמתים במעגל (דהיינו יש לנו משתנה לכל צומת של \( C \) והפולינום \( p \) משתמש בחלק מהם) כך שכל הצבה למשתנים שמתאימה למה שקורה במעגל מחזירה 0.

במאמר מסמנים ב-\( I\left(C\right) \) את קבוצת כל הזהויות הפולינומיות שמתאימות למעגל \( C \) מסויים. זו הגדרה סטנדרטית בתחום שנקרא גאומטריה אלגברית: שם בהינתן קבוצת נקודות \( V \) במרחב כלשהו, מסמנים ב-\( I\left(V\right) \) את אוסף כל הפולינומים שמתאפסים מעל המרחב הזה. האוסף הזה הוא אידאל: אם שני פולינומים מתאפסים על אותן נקודות, אז גם הסכום שלהם יתאפס על אותן נקודות, וכמובן שאם \( p\left(a\right)=0 \) ו-\( q \) הוא פולינום כלשהו, אז \( \left(pq\right)\left(a\right)=0 \) גם כן (כי מקבלים את המכפלה של 0 ב-\( q\left(a\right) \) שלא משנה מה הוא).

רוצים לדעת אם המעגל \( C \) מקיים תכונה כלשהי שניתן לנסח בתור זהות פולינומית? יפה! כל מה שנשאר לעשות הוא לבדוק שייכות לאידאל \( I\left(C\right) \). במאמר מדגימים את זה עבור התכונה של “המעגל מבצע פעולת כפל”. כדי לנסח את זה, מסמנים את הקלטים של המעגל ב-\( a_{0},a_{1},\dots,a_{n-1},b_{0},b_{1},\dots,b_{n-1} \) - שתי סדרות של \( n \) ביטים שמקודדות שני מספרים, \( a,b \). אם המעגל מחשב את \( c=ab \) אז התוצאה עשויה להיות בת \( 2n \) ביטים, ולכן הפלט של המעגל יהיה \( c_{0},c_{1},\dots,c_{2n-1} \). חוץ מזה יהיו במעגל גם שערים פנימיים עם משתנים נוספים שמתאימים להם, אבל זה פחות קריטי. עכשיו, הביטו בפולינום הבא:

\( \sum_{k=0}^{2n-1}2^{k}c_{k}-\left(\sum_{k=0}^{n-1}2^{k}a_{k}\right)\left(\sum_{k=0}^{n-1}2^{k}b_{k}\right) \)

הפולינום הזה מקודד בדיוק את הטענה ש-\( c=ab \), ולכן הבדיקה של “האם המעגל מבצע כפל” היא בדיוק בדיקת שייכות של הפולינום הזה ל-\( I\left(C\right) \).

אתם עשויים לשאול, כמובן, על מה כל המהומה הזו. האם אין פשוט שיטה אחת וזהו לבצע כפל באמצעות מעגל? ובכן, לא. יש דרכים רבות ושונות ומסובכות שמושפעות מאילוצים שונים ומשונים על המעגל ואני מעדיף לא להיכנס לזה בכלל. סמכו עלי שאפילו השאלה הזו של האם מעגל מבצע כפל יכולה להיות מעניינת. אתם גם עשויים לשאול אם לא פשוט יותר להציב את כל הערכים האפשריים ולבדוק - ובכן, חשבו על כך שערך טיפוסי עבור \( n \) הוא 64, מה שאומר שאין שום סיכוי שנוכל לעבור סדרתית על כל הקלטים האפשריים למעגל.

איך בודקים שייכות של פולינום לאידאל? כשמדובר על חוג פולינומים במספר משתנים מעל שדה, אפשר להראות שלכל אידאל קיים בסיס מיוחד, שנקרא בסיס גרובנר, שנותן אלגוריתם שמאפשר לבדוק שייכות של פולינום כלשהו לאידאל, על ידי משהו שמזכיר מעין חילוק ארוך עבור פולינומים במספר משתנים. זה נושא מרתק שראוי לפוסט משל עצמו, ולכן לא אכנס כרגע להגדרות. עבור \( I\left(C\right) \) המדובר כאן קיים בסיס גרובנר פשוט למדי, שכולל את הזהויות הפולינומיות שמתאימות לשערי המעגל - אותן הזהויות שכתבתי למעלה. בנוסף לכך הוא כולל גם פולינומים שהמטרה שלהם היא לומר “הקלט הוא או 0 או 1”: הפולינום \( p\left(x\right)=x\left(x-1\right) \) משיג את המטרה הזו - החליפו את \( x \) ב-\( a_{i} \) או \( b_{i} \) כלשהו כדי לקבל את כל הפולינומים מהצורה הזו שמתווספים לבסיס.

המאמר לא נגמר בנקודה הזו; הוא בקושי מתחיל. כל זה הוא רק ההקדמה התיאורטית, שאחריה באה ההסתייגות הרגילה של “אבל גם עם בסיס גרובנר, זו עדיין בעיה קשה חישובית לבדוק שייכות של פולינום לאידאל” (“קשה חישובית” כאן פירושו NP-קשה). בשל הקושי הזה המשך המאמר מתמקד בשיטה שרלוונטית ספציפית לבדיקת מכפילים ומשתמשת בתעלולים שמשפרים את ביצועי החישוב, אבל לא אכנס אליהם כאן. הנקודה המעניינת שרציתי להדגים פה היא האופן שבו חוגים ואידאלים (וספציפית חוגי פולינומים במספר משתנים ובסיס גרובנר) צצים “בשטח”, גם במקומות לא לגמרי צפויים.