בעיית יוספוס

בעיית יוספוס, על שם ההיסטוריון יוספוס פלביוס, היא ההוכחה שמתמטיקאים יכולים למצוא בעיה מתמטית בכל סיפור שרק נותן להם שמץ של הזדמנות לעשות זאת. במקרה הזה, הספר “תולדות מלחמת היהודים עם הרומאים” של יוספוס שמתאר את המרד הגדול ברומאים. בזמן המלחמה הזו פלביוס עדיין נקרא יוסף בן מתיתיהו והיה אחד ממפקדי הצבא היהודי, אך לבסוף ("תולדות מלחמת היהודים עם הרומאים", ספר 3, פרק שמיני) הובס על ידי הרומאים ביודפת ומצא את עצמו מסתתר במערה עם ארבעים אנשים.

כשהיה ברור לאנשים במערה שהרומאים עומדים ללכוד אותם, החליטו שעדיף להם להתאבד מאשר ליפול בידיהם. חוץ מאשר יוספוס שלא התלהב כל כך מכל הקטע הזה של מות קדושים וניסה להסתלק אבל לא בדיוק נתנו לו (“מהרו אליו מכל עברים בחרבות שלופות וחרפו אותו על מרך-לבו”).

אלא ש”גם בעת המצוקה הזאת לא נבצרה מזימה מיוסף” והוא הציע שאם כבר עליהם למות, שיעשו זאת בהגרלה. בכל סיבוב של ההגרלה ייבחר אדם אחד, שיהרוג את האדם שנבחר קודם (“הבו ונטיל גורלות, מי ממנו ימית את חברו. והנלכד בגורל יפול בחרב הבא אחריו”), וכך זה יימשך עד שכולם מתים. וכך הנה, ורצה הגורל שיוסף ואדם אחד יחיד נותרו בחיים עד הסוף (“אולי היה זה מקרה ואולי אצבע אלוהים”) ויוסף הצליח לשכנע את האדם האחר לא להשתתף בהימור, וכך ניצלו חייו (של יוסף; לא בדיוק מסופר מה עלה בגורל השני ומכיוון שמדובר ברומאים אני לא אופטימי).

בתור סיפור, זה סיפור מוצלח למדי, למי שאוהבים דם ואש ותמרות עשן; אבל כמה הוא אמין? והאם אפשר לחלץ מפה חידה מתמטית מעניינת?

ראשית, מה הסיכוי של יוסף לשרוד הרפתקאה כזו ב”מקרה”, כדבריו? על פי הסיפור, היו עם יוסף 40 אנשים נוספים, כלומר בסך הכל היו 41. אם ההגרלה שבוצעה היא הוגנת, הסיכוי של יוסף להיות האחרון ששורד הוא \( \frac{1}{41}\approx2.44\% \) - ממש לא משהו. איך הגעתי למספר הזה? דרך אחת היא פשוט לומר שלכל האנשים אותו סיכוי בדיוק; דרך מסורבלת יותר עם פחות נפנוף ידיים היא להגיד שכל הגרלה יוצרת סידור בשורה של האנשים - האיש הראשון, האיש השני וכן הלאה, מה שנקרא בקומבינטוריקה תמורה. יש \( 41! \) תמורות כאלו, כאשר סימן הקריאה מתאר את פעולת העצרת: \( n!=1\cdot2\cdot3\cdots n \). אם נספור רק את התמורות שבהן יוסף הוא אחרון, נראה שיש \( 40! \) כאלו, כי פשוט מסדרים בשורה את כל האנשים מלבד יוסף, ואז מוסיפים אותו בסוף. לכן יש ליוסף סיכוי של \( \frac{40!}{41!}=\frac{1}{41} \) להישאר אחרון.

אבל רגע, יוסף סיפר שנשאר איתו עוד אדם אחד. אם נניח שלא משנה איזה אדם היה שורד עם יוסף, די בכך שנשאר רק אחד נוסף כדי שיוסף יוכל לשכנע אותו, הסיכוי של יוסף לשרוד גדל פי 2; עכשיו כדי לקבל תמורה שבה הוא שורד, מסדרים את 40 האנשים האחרים בשורה ואז בוחרים אחד משני המקומות האחורנים בשביל יוסף ומסדרים את האחרים “סביבו” (או כולם לפניו, או שהאחרון בסידור של האנשים האחרים יהיה אחריו) ויוסף מקבל סיכוי של \( \frac{2\cdot40!}{41!}=\frac{2}{41}\approx4.88\% \) לשרוד (ובאופן כללי, אם יוסף היה מצליח לשכנע את הנותרים כשנשארו \( k \) אנשים, אז הסיכוי שלו לשרוד היה \( \frac{k\cdot40!}{41!}=\frac{k}{41} \)).

העניין הוא שגם \( 4.88\% \) הוא לא סיכוי גדול במיוחד. במילים אחרות, אנחנו לא מאמינים ל”אולי היה זה מקרה ואולי אצבע אלוהים” של יוסף ומעדיפים לחשוב עליו בתור תחמן שהצליח איכשהו להנדס את ההגרלה לטובתו. הבעיה היא שאנחנו לא יודעים מה הייתה ההגרלה - יוסף לא מספר לנו שום דבר מעבר ל”הבו ונטיל גורלות”. אז מה עושים? ממציאים! איכשהו בפולקלור המתמטי השתרשה גרסה מאוד ספציפית של הגרלה שבה לכאורה השתמשו בסיפור הזה, והמתמטיקה מתעניינת בדיוק במחקר של סוג ההגרלה הזה.

בהגרלה הזו האנשים עומדים במעגל - נסמן אותם בתור המספרים מ-1 עד 41 (יש גרסאות מתמטיות שמתארות את הסיפור עם מספר שונה של אנשים, אבל המספר מהסיפור של יוסף עצמו הוא 41). בוחרים מספר כלשהו, נאמר 3 (גם פה, בגרסאות מתמטיות שונות ומשונות משתמשים גם במספרים אחרים), ואז מתחילים לעבור על המעגל 3 צעדים בפעם. בפעם הראשונה מגיעים אל איש מס’ 3 ומסירים אותו מהמעגל (אני אוותר על תיאורים אלימים יותר); אחר כך אל איש מספר 6 ומסירים גם אותו, וכך זה נמשך; אנו מסירים מהמעגל את אנשים \( 3,6,9,12,15,18,21,24,27,30,33,36,39 \) ולכאורה האיש הבא שנסיר אמור להיות מס’ 42, אבל אין במעגל 42 אנשים אלא רק 41, אז מתחילים מחדש ומסירים את איש מס’ 1. עכשיו נראה שהבא בתור הוא 4, אבל זה לא מה שקורה. כזכור, כבר הסרנו מהמעגל את איש מס’ 3, ולכן אם נספור שלושה צעדים החל מאיש מס’ 1, נקבל את איש 2, איש 4 ואיש 5, ולכן 5 הוא הבא בתור שיוסר מהמעגל, וכן הלאה.

בשיטה הזו בכלל אין חשיבות למזל. היא מרגישה קצת אקראית במובן זה שהיא יוצרת לנו תמורה כלשהי של האנשים, שאחרי הסיבוב הראשון סביב המעגל כבר נראית “מבולגנת”, אולם בתיאוריה, מי שיודע שיש 41 אנשים והולכים לעבור 3 בכל פעם יכול לעשות חישוב מהיר בראש ולגלות את המקום שבו כדאי לו להיות במעגל כדי להיות זה שנשאר אחרון.

האם זה מה שיוסף עשה, והוא גם מחשב אנושי בנוסף להיסטוריון מחונן? ובכן… כנראה שלא. כאשר יוסף נשאר עם האדם הבודד הנוסף, הוא אומר שהוא “לא רצה להלכד בגורל ולמות, וגם לא לטמא את ידו בדם אחים אם ישאר האחרון”. אבל הרי אם הייתה ננקטת שיטה דטרמיניסטית, בשלב הזה יוסף בודאות כבר היה יודע אם הוא יישאר האחרון או לא; כלומר, נראה שבכל שלב בוצעה הגרלה חדשה, בשונה מהשיטה של המעגל. אלא שזה לא משנה לנו כי עם כל הכבוד לסיפור המעניין של יוסף, אנחנו פה בשביל חידת המעגל עצמה.

אם כן, מה המטרה שלנו בחידה? באופן כללי, לכל מספר אנשים \( n \) ומספר צעדים \( q \) אנחנו מקבלים תמורה \( J_{n,q} \), ויכולים לשאול את עצמנו כל מני שאלות עליה - איך מחשבים אותה? מה האיבר האחרון בה? מה המבנה שלה? וכדומה. זה תחום רחב שלא ידוע עליו יותר מדי במקרה הכללי, ולכן אספר כמה סיפורים ספציפיים שקשורים אליו, ונתחיל ממה שאני מחבב במיוחד: במקרה שבו \( q=2 \), כלומר מתקדמים במעגל שני צעדים בכל פעם, איך אפשר לחשב מה המקום של האדם האחרון שיישאר במעגל, מבלי לחשב את כל \( J_{n,2} \)?

מה שיש לנו פה בעצם הוא סדרה של מספרים - לכל \( n \), מתאים המיקום שתקף לאותו מספר אנשים \( n \). בואו נסמן ב-\( a_{n} \) את אברי הסדרה הזו. לפנינו בעיה קומבינטורית סטנדרטית - למצוא חוקיות בתוך סדרת מספרים. איך עושים את זה? דבר ראשון שתמיד כדאי לעשות - לחשב כמה ערכים ראשונים, פשוט על ידי כך שמשחקים את המשחק. בבירור \( a_{1}=1 \) (כי אדם בודד הוא כבר האחרון) ו-\( a_{2}=1 \) (כי בשלב הראשון הולכים שני צעדים, שהראשון חולף על פני 1 והשני מגיע אל 2 ומוציא אותו) ו-\( a_{3}=3 \) וכך נמשיך ונקבל את הסדרה:

\( 1,1,3,1,3,5,7,1,3,5,7,9,11,13,15,1,3,5,7,\ldots \)

לא טרחתי לחשב את הסדרה בעצמי, כמובן; קל לכתוב קוד (למשל, בפייתון) שמייצר אותה:

def josephus_permutation(n,q):
    people = list(range(1,n+1))
    location = 0
    result = []
    while len(people) > 0:
        location = (location + q - 1) % len(people)
        result.append(people.pop(location))
    return result
print([josephus_permutation(n,2)[-1] for n in range(1,20)])

עכשיו, הסדרה נראית כמו ערבוביה גדולה אבל כמה דברים ברורים - קודם כל, יש מספרים שחוזרים על עצמם המון, אפילו בסוג של מחזוריות. שנית, כל המספרים הם אי זוגיים. אלו אבחנות פשוטות ולא מפתיעות אבל הן מצביעות על כך שיש פה סדר שאפשר למצוא. בואו נחשוב על זה - למה כל המספרים אי זוגיים? כמובן, כי מאחר ו-\( q=2 \) הרי שבסיבוב הראשון של ה”משחק” נפטרים מכל הערכים הזוגיים שהיו. למשל, אם \( n=8 \) אז הסיבוב הראשון מסלק את \( 2,4,6,8 \) ואז בסיבוב השני נשארנו עם \( 1,3,5,7 \) (שמתוכם נסיר את \( 3,7 \) ובסיבוב השלישי נסיר את \( 5 \)). בשלב הזה האינטואיציה המתמטית עשויה לקפוץ - הסיבוב הראשון בעצם מייצר לנו בעיית יוספוס חדשה, עם חצי ממספר האיברים בבעיה המקורית.

מהבעיה \( n=8 \) עברנו אל בעיה קצת מוזרה, שבה \( n=4 \) אבל האיברים לא ממוספרים בתור \( 1,2,3,4 \) אלא בתור \( 1,3,5,7 \). מה הקשר בין שתי הסדרות הללו, \( 1,2,3,4 \) ו-\( 1,3,5,7 \)? זה לא קשר של שוויון, אבל אפשר לנחש שיש קשר פשוט ולראות אם זה עובד בפועל. קשר פשוט במיוחד הוא קשר לינארי, \( y=ax+b \) כאשר \( a,b \) הם קבועים. מספיק להציב ערכי \( x,y \) עבור שני האיברים הראשונים בסדרה כדי להסיק מה \( a,b \) חייבים להיות אם הקשר אכן מתקיים:

\( 1=a\cdot1+b \)

\( 3=a\cdot2+b \)

נחסר את המשוואה הראשונה מהשניה ונקבל \( 2=a \) ואז נציב את זה במשוואה הראשונה ונקבל \( 1=2\cdot1+b \), כלומר \( b=-1 \). במילים אחרות, אנחנו מנחשים שמתקיים הקשר הפשוט \( y=2x-1 \). בדיקה זריזה תראה שהוא אכן מתקיים.

ייתכן שזה נראה מיותר לגמרי - שאפשר לראות “בעין” שזה הקשר בין \( 1,2,3,4 \) ובין \( 1,3,5,7 \), ולחלקנו זה כנראה המצב; אבל מה שנחמד פה הוא שגם לניחושים ואינטואיציות כאלו יש דרך שיטתית שבה אפשר להגיע אליהם.

אם כן, גילינו שיטה שבה אפשר לצמצם את ממדי בעיית יוספוס: לחלק את מספר האיברים ב-2 לקבלת בעיה קטנה יותר, לקחת את התוצאה שלה, להכפיל ב-2 ולהחסיר 1. או בניסוח מתמטי:

\( a_{2n}=2a_{n}-1 \)

קל לבדוק שזה עובד לכל \( n \) - אבל הנוסחה הזו מטפלת רק במקרים שבהם התחלנו עם מספר זוגי של שחקנים. מה קורה במקרה האי זוגי, כלומר עבור \( a_{2n+1} \)?

ובכן, שוב כדאי להסתכל על דוגמא, נאמר עבור \( 1,2,3,4,5,6,7,8,9 \). כאן אחרי הסיבוב הראשון נישאר עם \( 1,3,5,7,9 \), כשהבא בתור יהיה 1. בואו נסלק גם את ה-1 הזה מהתמונה, ונישאר עם \( 3,5,7,9 \). קיבלנו 4 איברים כמו קודם, רק שעכשיו ההתאמה שלו צריכה להתאים את \( 1,2,3,4 \) אל \( 3,5,7,9 \) - חישוב זריז יראה שהפעם צריך לכפול ב-2 ולחבר 1, ונקבל

\( a_{2n+1}=2a_{n}+1 \)

המסקנה שלנו היא שאפשר לתת נוסחת נסיגה פשוטה עבור \( a_{n} \):

\( a_{n}=\begin{cases} 1 & n=1\\ 2a_{k}-1 & n=2k\\ 2a_{k}+1 & n=2k+1 \end{cases} \)

הנוסחה הזו מאפשרת לנו לחשב את הרשימה \( 1,1,3,1,3,5,7,1,3,5,7,9,11,13,15,1,3,5,7,\ldots \) הרבה יותר בקלות. הנה קוד שעושה את זה:

a = [1]
for n in range(2,20):
    a.append(2*a[n // 2 - 1] + (-1 if n % 2 == 0 else 1))
print(a)

זה לכשעצמו כבר מאפשר לנו לחשב בקלות את הפתרון של בעיית יוספוס גם עבור ערכים גבוהים מאוד, אבל יש דרך לעשות את זה עוד יותר נחמד. אז בואו נראה אותה. אנחנו רוצים “לפתור” את נוסחת הנסיגה - לקבל דרך לחשב את \( a_{n} \) ישירות מתוך \( n \), בלי לעבור דרך ערכים קטנים יותר.

ראשית, בואו נסתכל שוב על רשימת המספרים:

\( 1,1,3,1,3,5,7,1,3,5,7,9,11,13,15,1,3,5,7,\ldots \)

אמרנו כבר שרואים פה חזרתיות. עכשיו אולי יהיה יותר קל להבין מאיפה היא מגיעה. נוסחת הנסיגה בעצם אומרת לנו שלמעט האיבר הראשון, כל זוג אברים אחר כך יגיע בתור צמד מהצורה \( 2a_{k}\pm1 \) כאשר \( a_{k} \) הוא איבר מוקדם יותר. לי קל לדמיין את זה במבנה של עץ בינארי, כשלוקחים את האיבר הראשון בסדרה לצומת העליון, את שני הבאים להיות הבנים שלו, את ארבעת הבאים להיות הבנים של הבנים, וכן הלאה:

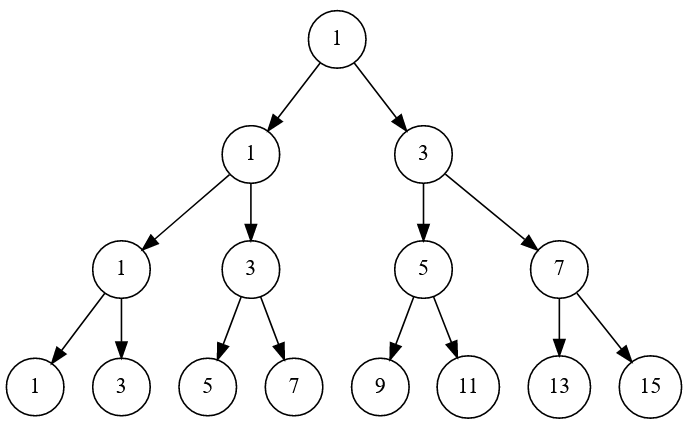
בצורה הזו רואים שאפשר לחלק את המספרים בסדרה לקבוצות מגודל \( 2^{k} \) (כאשר \( k \) הוא מספר השורה שלהן, החל משורה 0):

\( 1 \)

\( 1,3 \)

\( 1,3,5,7 \)

\( 1,3,5,7,9,11,13,15 \)

וכל שכבה פשוט חוזרת על כל המספרים האי-זוגיים מ-1 ועד שהיא מתמלאת.

בניסוח מתמטי פורמלי אפשר לומר זאת כך: \( a_{2^{k}+m}=2m+1 \), כאשר \( m<2^{k} \).

קיבלנו נוסחה סגורה יפה עבור \( a_{n} \), אבל אפשר להציג אותה בצורה עוד יותר יפה אם חושבים לרגע על מה היא בעצם עושה. בשביל זה כדאי להסתכל על הייצוג הבינארי של \( n \).

ייצוג בינארי של מספר הוא כתיבה שלו בתור סכום של חזקות של 2. כשאני כותב “1101” אני מדבר על הסכום \( 1\cdot2^{0}+0\cdot2^{1}+1\cdot2^{2}+1\cdot2^{3}=1+4+8=13 \). עכשיו, אם ידוע לי ש-\( n \) הוא מספר מהצורה \( 2^{k}+m \) כאשר \( m<2^{k} \), מה זה אומר על הייצוג הבינארי של \( n \)? זה אומר שהייצוג הזה כולל \( k \) ספרות כשהספרה ה-\( k \)-ית היא 1, ויתר הספרות מרכיבות את המספר \( m \). זה אומר שאם אני אקח את הייצוג הבינארי הזה ואמחק ממנו את הספרה האחרונה הזו, אני אקבל את הייצוג הבינארי של \( m \) עצמו.

עכשיו, אם אני לוקח מספר וכופל אותו ב-2, הייצוג הבינארי שלו זז צעד אחד שמאלה: אם אני כופל את 1101 ב-2 אני מקבל 11010. אם אני לוקח את זה ומוסיף לו 1, אני משנה את הספרה הימנית ביותר מ-0 ל-1. לכן את הנוסחה \( a_{2^{k}+m}=2m+1 \) אפשר לתאר גם בצורה הבאה:

בהינתן \( n \), קחו את הייצוג הבינארי שלו, הסירו מהמספר את ה-1 השמאלי ביותר והכניסו אותו מחדש במקום הימני ביותר. קיבלתן את הייצוג הבינארי של \( a_{n} \). למשל, ראינו שהייצוג הבינארי של 13 הוא 1101 ולכן אחרי התעלול נעבור אל 1011, שהוא הייצוג הבינארי של \( 1+2+8=11 \). כך אנו יודעים שבמקום ה-13 בסדרה יהיה האיבר 11.

עכשיו קיבלנו משהו שיוסף היה יכול לעשות בראש, אילו באמת היו משתמשים בשיטה הזו עם \( q=2 \). היו במעגל 41 אנשים, והייצוג הבינארי של 41 הוא 101001 (את זה אפילו אני מצליח לחשב בראש) ולכן המקום שיישאר אחרון הוא 10011, שהוא המספר \( 16+2+1=19 \), ולכן זה המקום שיוסף היה צריך להיות בו.

שימו לב שבמעבר מ-101001 אל 10011 “איבדנו” ספרה - זה כי אחרי הסרת ה-1 השמאלי ביותר מ-101001 נשארנו עם 01001, והאפס השמאלי הזה מתפוגג לו. זה בעצם מלמד אותנו מה יקרה אם נשחק את המשחק שבו אנו מתחילים עם \( n \), מחליפים אותו ב-\( a_{n} \), מחליפים אותו ב-\( a_{a_{n}} \) וכן הלאה - אנחנו הולכים לקחת את המספר \( n \) ולהעביר 1-ים משמאל לימין תוך שאנו מאבדים את כל האפסים בדרך, ואחרי מספר סיבובים ששווה למספר הספרות הבינאריות של \( n \) נישאר עם מספר שכולו 1-ים, כמספר ה-\( 1 \)-ים שהיו ב-\( n \) במקור. פורמלית, נגיע אל \( 2^{\#_{1}\left(n\right)}-1 \) כאשר \( \#_{1}\left(n\right) \) הוא מספר ה-1-ים בייצוג בינארי של \( n \).

זו התוצאה שרציתי להציג בפוסט, למרות שאפשר לשאול עוד הרבה שאלות אחרות על בעיית יוספוס, אבל במהלך קריאה של דברים לקראת כתיבת הפוסט נתקלתי במשהו שהוא כל כך הזוי ממבט ראשון שאני חייב לספר גם עליו, אם כי הוא ידרוש גלישה למונחים טכניים מתקדמים יחסית.

התוצאה הזו מוזכרת בספר Matters Mathematical של Herstein ו-Kaplansky. הם מציבים לעצמם למטרה להתעניין לא בפתרון ל”בעיית יוספוס” (מי נשאר אחרון) אלא בהבנת המבנה של התמורה \( J_{n,q} \) כולה. בפרט, לכל תמורה הם מפרקים אותה למבנה המעגלי שלה.

למשל, את \( J_{11,2} \) אפשר לתאר בתור הרשימה \( 2,4,6,8,10,1,5,9,3,11,7 \). הרשימה הזו היא דרך פשוטה לומר “1 עובר ל-2, 2 עובר ל-4, 3 עובר ל-6” וכן הלאה. כשרוצים לתאר דבר כזה בתור מעגל פשוט מתחילים מאיבר כלשהו ורואים לאן הוא עובר, ולאן עובר מי שהוא עובר אליו, וכן הלאה - עד שחוזרים לאיבר שהתחלנו ממנו, ואז בוחרים איבר שטרם בחרנו ופותחים מעגל חדש. אם נעשה את זה על \( J_{11,2} \) נקבל את הייצוג \( \left(1\ 2\ 4\ 8\ 9\ 3\ 6\right)\left(5\ 10\ 11\ 7\right) \) כלומר, קיבלנו שני מעגלים, שהאחד הוא מאורך 7 והשני הוא מאורך 4.

הרשטיין וקפלנסקי מתארים כמה תוצאות על התמורות הללו. למשל, אם \( n\equiv1\left(\text{mod }4\right) \) (כלומר, כשמחלקים את \( n \) ב-4 מקבלים שארית 1) ובנוסף לכך גם \( n \) וגם \( 2n+1 \) הם ראשוניים, אז \( J_{n,2} \) תורכב ממעגל אחד גדול (זה קורה עבור \( J_{5,2} \), למשל). אבל התוצאה המעניינת ביותר שלהם נוגעת למקרה של \( n\equiv3\left(\text{mod }4\right) \) כך ש-\( n \) ו-\( 2n+1 \) שניהם ראשוניים (למשל \( n=11 \) שבדוגמא שלי). במקרה כזה אפשר להוכיח שיהיו בדיוק שני מעגלים בפירוק. והנה רשימה של האורכים של המעגלים הללו עבור ערכים קטנים של \( n \) שמקיימים את התנאי:

\( \begin{array}{cc} 3: & 2,1\\ 11: & 7,4\\ 23: & 14,9\\ 83: & 47,36\\ 131: & 72,59\\ 179: & 99,80\\ 191: & 104,87\\ 239: & 132,107\\ 251: & 136,115 \end{array} \)

קיבלנו כאן רשימה די מוזרה של מספרים אקראיים לכאורה. מתמטיקאים אוהבים למצוא סדר בדברים האקראיים לכאורה, וכאן הסדר הוא מפתיע למדי וקשור אל תורת המספרים האלגברית. זה תחום עשיר ויפה שרק נגעתי בקצה-קצהו בבלוג, אבל לשמחתי ברמה שמקיפה את כל המושגים שבהם אשתמש עכשיו.

בתורת המספרים האלגברית מתעסקים במשהו שנקרא חוגי שלמים. בלי להיכנס להגדרה המלאה (כי אני מחביא פה כל מני מורכבויות לא רלוונטיות), אם ניקח את \( \mathbb{Z} \) ונרחיב אותו על ידי הוספת מספר “מבחוץ” כמו \( \sqrt{-11} \), ונקבל את מה שמסומן בתור \( \mathbb{Z}\left[\sqrt{-11}\right] \): אוסף כל האיברים מהצורה \( a+b\sqrt{-11} \) כך ש-\( a,b\in\mathbb{Z} \), התוצאה תהיה מבנה אלגברי שנקרא חוג שיש בו פעולות כפל וחיבור. כך למשל

\( \left(a+b\sqrt{-11}\right)\left(c+d\sqrt{-11}\right)=\left(ac-11bd\right)+\left(ad+bc\right)\sqrt{-11} \)

החוגים שמתקבלים בצורה הזו הם מעניינים מאוד, ואפשר לחקור אותם באמצעות כלים דומים לאלו שבהם חוקרים את \( \mathbb{Z} \) עצמו, אבל מהר מאוד מגיעים לחוגים שבהם אחד הכלים הבסיסיים ביותר שלנו נשבר. ב-\( \mathbb{Z} \) יש למספרים מה שנקרא פריקות יחידה, כלומר כל מספר שלם ניתן להצגה בצורה אחת ויחידה בתור מכפלה של אי-פריקים. בחוגי שלמים כלליים יותר, לא בהכרח. הדוגמא הקלאסית היא החוג \( \mathbb{Z}\left[\sqrt{-5}\right] \) שבו \( 6=2\cdot3=\left(1+\sqrt{-5}\right)\left(1-\sqrt{-5}\right) \) הם שני פירוקים שונים של 6 לאי-פריקים.

בלי פריקות יחידה, הרבה מתורת המספרים נזרק לפח, וזה מאוד מצער. לכן תורת המספרים האלגברית מוצאת דרך לתקן חלקית את הבעיה. במקום לדבר על פריקות יחידה של מספרים לאי-פריקים, מדברים על פריקות שלהם לאידאלים, כשאידאלים הם קבוצות של מספרים בעלי תכונות מסויימות (אינטואיטיבית אפשר לחשוב על אידאלים בתור משהו שאפשר לפרק אליו אי-פריקים כדי שפירוקים שאינם יחידים יגיעו בסוף לאטומים עוד יותר בסיסיים שכן יהיו משותפים). למרבה השמחה, בחוגי השלמים זה אכן מחזיר את מושג הפריקות היחידה; רק נשאר להבין מה אנחנו מאבדים במעבר מפריקות יחידה לאי-פריקים אל פריקות יחידה לאידאלים.

כאן נכנסת לתמונה חבורה שנקראת Ideal Class Group (“חבורת מחלקות האידאלים”?) שבמובן מסויים מתארת את האופן שבו הפריקות היחידה “נשברת” - ככל שהיא יותר גדולה ומסובכת, כך הפריקות היחידה הרוסה יותר (וה”מחיר” של תיקון שלו כדי לשמר חלק מהמתמטיקה שלנו יהיה כרוך בויתורים גדולים יותר). הקטע הזה של פריקות יחידה לאידאלים קיים במחלקה רחבה של חוגים, שנקראים חוגי דדקינד; מה שיפה בחוגי שלמים ספציפית הוא שבהם החבורה הזו יחסית נחמדה - בפרט, היא סופית. הגודל שלה נקרא “מספר המחלקה”, Class Number.

איך כל זה קשור אל בעיית יוספוס? פשוט מאוד, נכון שאמרתי שעבור ערכי \( n \) כך ש-\( n,2n+1 \) שניהם ראשוניים, \( n\equiv3\left(\text{mod }4\right) \) אז התמורה \( J_{n,2} \) מורכבת בדיוק משני מעגלים, וכתבתי רשימה של אורכי המעגלים הללו?

\( \begin{array}{cc} 3: & 2,1\\ 11: & 7,4\\ 23: & 14,9\\ 83: & 47,36\\ 131: & 72,59\\ 179: & 99,80\\ 191: & 104,87\\ 239: & 132,107\\ 251: & 136,115 \end{array} \)

אז אם ניקח \( n \) ונסתכל בחוג השלמים \( \mathbb{Z}\left[\sqrt{-\left(2n+1\right)}\right] \), נקבל שמספר המחלקה שלו שווה להפרש בין גדלי שני המעגלים שמרכיבים את \( J_{n,2} \). למשל, עבור \( n=11 \) נקבל שמספר המחלקה של \( \mathbb{Z}\left[\sqrt{-23}\right] \) הוא \( 7-4=3 \).

מה הולך פה? אין לי מושג, לא קראתי את ההוכחה. אני מניח שאחרי שרואים את ההוכחה התוצאה הזו הרבה פחות מפתיעה, אבל כרגע היא עבורי סוג של קסם - קישור שממש לא ציפיתי לו בין שני תחומים לכאורה שונים במתמטיקה. קצת מזכיר את עניין ה-Monstrous Moonshine המפורסם שכתבתי עליו בבלוג. במתמטיקה דברים כאלו הם חלק מהכיף.