מה בעצם הולך בטריגונומטריה בתיכון? (חלק א')

מבוא

אני רוצה להתמודד עם אחת מטראומות המתמטיקה הגדולות שלי, אם לא הגדולה מכולן - טריגונומטריה תיכונית. ואני חושב שאין דבר שמעביר את גודל הטראומה טוב יותר מאשר צפייה בדף הנוסחאות לטריגונומטריה:

מה הולך כאן? ובכן, אנחנו מייד רואים שיש לנו עסק עם שני יצורים לא ברורים שנקראים \( \sin \) ו-\( \cos \) שעושים כל מני… דברים… שמערבים המון סימני פלוס ומינוס שנראים אקראיים לגמרי, ויש גם איזה “רדיאנים” שנכנסים לתמונה פה. עכשיו, תגידו, זו דרך לא הוגנת להציג טריגונומטריה! אחרי שלומדים את המושגים עצמם ומגיעים לפתרון תרגילים הכל מתבהר! ובכן, לא. היכרות עמוקה יותר עם החומר מתבטאת בהיכרות עם עוד נוסחאות מזעזעות במידה דומה, ועם תרגילים בסגנון “הוכיחו את הזהות \( \sin^{2}3\alpha-\sin^{2}\alpha=\sin2\alpha\sin4\alpha \)”.

מכאן קצרה הדרך לשאלה המצמיתה - בשביל מה צריך את זה. האם בחיי היומיום שלנו נוכיח זהויות טריגונומטריות? לא! אף פעם! ובכן, אולי אם נלך לאוניברסיטה ונלמד שם, נאמר, מתמטיקה ומדעי המחשב נזדקק לזה? ובכן, בקושי רב. ולרוב ברמה מאוד בסיסית. ובכן, אולי במקצועות מדעיים או הנדסיים אחרים צריך את זה ברמת אינטנסיביות גדולה יותר? ייתכן, אבל אז למה לא ללמוד את זה באופן ייעודי רק שם? אין תשובה טובה לשאלות הללו. כפי שכבר אמרתי בעבר, אין לי תשובה טובה לשאלה מה צריך ללמד או לא ללמד בבית הספר כי זה נושא סבוך בהרבה מאשר סתם “בואו נעיף את כל מה שמעצבן אותנו”. מבחינתי השאלה היא לא האם צריך ללמד את זה, אלא האם אפשר ללמד את זה ברור.

כאן, לדעתי, התשובה היא “כן”. אני מקווה שלפחות בחלק מבתי הספר מלמדים את זה יותר ברור מאשר זה היה לי; אבל אני לא יודע מה עושים בכלל בתי הספר ולכן אנסה לכתוב כאילו קהל היעד שלי הוא גדי מחטיבת הביניים שלא הבין כלום ושנא הכל, ונראה אם אני אצליח לגרום לנודניק הזה עם גישת האנטי שלו לשנוא קצת פחות את החומר. או שבדרך אני אתחיל לשנוא את החומר עוד יותר.

בואו נתחיל.

מה זה בכלל סינוסים וקוסינוסים?

הכוכבות המרכזיות של הטריגו הן שתי פונקציות שנקראות “סינוס” ו”קוסינוס” ומסומנות בתור \( \sin x \) ו-\( \cos x \). הכוונה ב”פונקציה” היא שלכל מספר \( x \) שאני נותן להן כקלט, הן מחזירות מספר כפלט. במתמטיקה, הפונקציות הללו מאוד חשובות; הן מופיעות באופן טבעי בהקשרים רבים ושונים, שהמשותף לכולם על פי רוב הוא קיום של מחזוריות כלשהי. דוגמא מוכרת יחסית מחיי היום יום היא זו של אקוולייזר של מוזיקה:

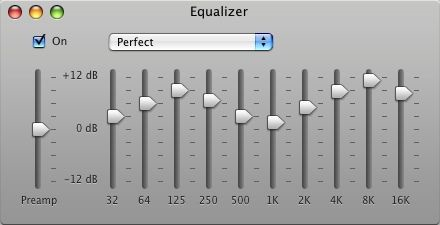
אקוולייזר יודע להחליש או להגביר תדירויות מסויימות של צליל, מה שמשפיע על האופן שבו אנחנו שומעים מוזיקה (למשל, אפשר “לחזק את הבאסים”). הרעיון מאחורי אקוולייזר הוא שצליל, גם כזה מורכב, הוא בעצם גל מחזורי, ואפשר לפרק את הגל המורכב הזה לסכום של גלים פשוטים יותר ולחזק/להחליש כל אחד מהגלים הפשוטים הללו באופן אינדיבידואלי. התיאור של הגלים הפשוטים יותר הללו מתבסס על סינוס וקוסינוס (הדוגמא הזו היא מקרה פרטי של מה שנקרא “טורי פורייה”; קסם מתמטי שמאפשר לתאר את רוב הדברים המחזוריים בתור סכום שכזה של סינוסים וקוסינוסים פשוטים).

עוד מקום שבו סינוסים וקוסינוסים צצים באופן טבעי הוא למשל במה שקורה כשאנחנו מותחים משהו שמחובר לקפיץ, משחררים אותו ומביטים בתנועה (המחזורית!) שלו. אפשר לכתוב משוואות שמתארות את התנועה; אלו יהיו משוואות מורכבות יחסית, שנקראות משוואות דיפרנציאליות, והפתרון שלהן יוצא בדיוק סינוסים וקוסינוסים - כלומר, התיאור של התנועה של המשהו-שמחובר-לקפיץ ייעזר בסינוסים וקוסינוסים. כשהצגתי בעבר את הפונקציות הללו בבלוג, השתמשתי בגישה הזו.

העניין הוא שהדוגמאות הללו הן אולי מעניינות (אני מקווה) וחשובות אבל הן קשות. כשמגיעים ללמוד על טריגונומטריה בבית הספר עדיין אין את הרקע הנדרש כדי להיכנס לעובי הקורה הטכנית שלהן. בשל כך, האופן שבו מגדירים סינוסים וקוסינוסים הוא בעזרת משולש ישר זווית ועלול להתקבל רושם מוטעה שזו המהות היחידה של הפונקציות הללו. אז כאמור - זה לא כך, ואנחנו מתחילים ממשולשים פשוט כי זו הדרך הקלה ביותר עבורנו להגדיר באופן מדויק את הפונקציות הללו.

אז הרי לנו, משולש ישר זווית:

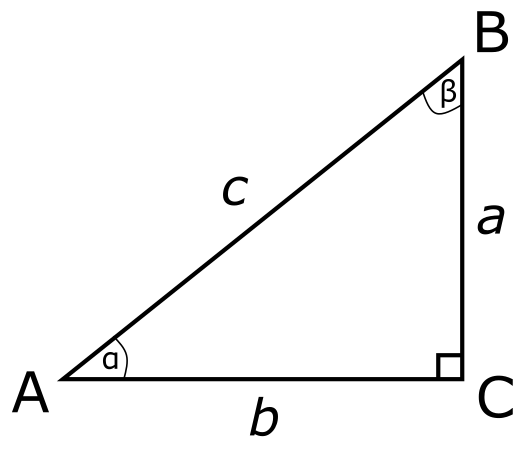
כדרכם של משולשים יש לו שלושה קודקודים \( A,B,C \) שיוצרים שלוש צלעות \( AB,AC,BC \) שהאורכים שלהן מתוארים עם \( a \) (עבור \( BC \)), עם \( b \) (עבור \( AC \)) ועם \( c \) (עבור \( AB \)). בנוסף יש למשולש שלוש זוויות (מה זו בעצם זווית? אני חושב עליה בתור “כמות סיבוב” אבל ההגדרה הטובה ביותר שאני מכיר היא - “נו, אתם יודעים”).הזווית \( \angle BAC \) שמסומנת באות היוונית \( \alpha \), הזווית \( \angle ABC \) שמסומנת באות היוונית \( \beta \), והזווית \( \angle ACB \) שלא מסומנת על ידי שום אות אלא על ידי ריבוע קטן כדי לציין שזו זווית ישרה - זווית בת \( 90^{\circ} \), רבע סיבוב שלם.

כאן נדרש הסבר קטן על איך מודדים זוויות. בפוסט הזה אני משתמש בשיטת מדידה שנקראת מעלות. מעלות מוגדרות כך שסיבוב שלם הוא בן 360 מעלות, וכותבים את זה \( 360^{\circ} \), כלומר עם עיגול קטן למעלה. למה 360? כי זה מספר נחמד שמתחלק בהמון דברים - יותר קליל להגיד “90 מעלות” במקום “\( \frac{1}{4} \) סיבוב” ויותר קליל להגיד “60 מעלות” במקום \( \frac{1}{6}" \) סיבוב” וכדומה. יש עוד שיטות מדידה לזווית, כשהחשובה והשימושית שבהן היא מדידה באמצעות רדיאנים. במדידה כזו, הזווית של סיבוב שלם היא בת \( 2\pi \) רדיאנים, כלומר מעלה אחת שווה ל-\( \frac{\pi}{180} \) רדיאנים. למה רדיאנים זו שיטה חשובה ושימושית? יש לי פוסט על זה ואולי אגיע לנושא הזה גם פה, אבל כרגע בואו נשכח לגמרי מהשיטה הזו - אנחנו לא צריכים אותה, ולדעתי יותר נוח לדבר על מעלות מאשר על רדיאנים בשלב הזה.

על הצלעות במשולש אנחנו אומרים שהן נמצאות מול זוויות מסויימות. הצלע \( BC \), שאורכה היה \( a \), נמצאת מול הזווית \( \alpha \); הצלע \( AC \) נמצאת מול \( \beta \); ואילו \( AB \) נמצאת מול הזווית הישרה. במשולש ישר זווית שכזה קוראים בשם היתר לצלע שמול הזווית הישרה, ושתי הצלעות האחרות הן הניצבים. אלו הרבה שמות וסימונים אבל נזדקק להם בהמשך.

עכשיו, משולשים ישרי זווית יכולים להגיע בשלל צורות וגדלים, הנה עוד כמה לדוגמא:

במשולשים הללו הזוויות שונות, וגם אורכי הצלעות שונים. הרעיון הבסיסי בסינוס וקוסינוס הוא שהם מאפשרים לתאר את הקשר בין הזוויות של משולש ישר זווית ובין האורכים של הצלעות שלו. אבל צריך להיזהר פה. בתור דוגמא, בואו ניקח את המשולש שראינו קודם ונשים לידו גרסה מוקטנת שלו:

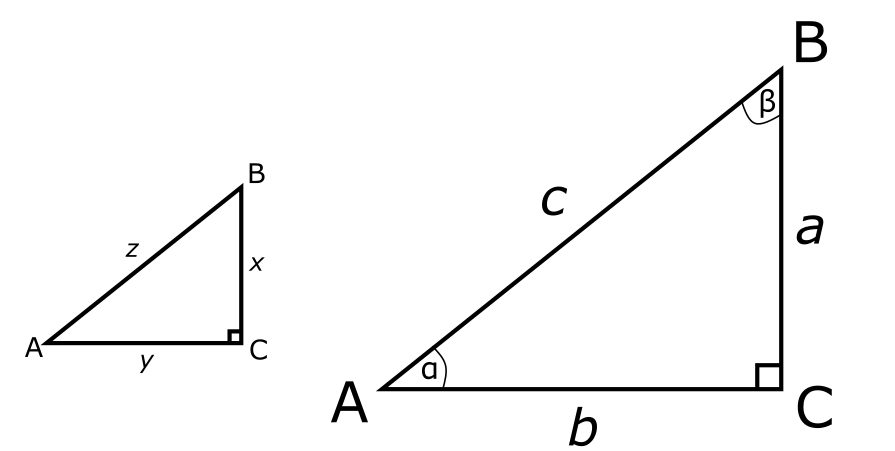
המשמעות של “גרסה מוקטנת” היא שאמנם הצלעות קטנות יותר, אבל הזוויות של שני המשולשים זהות. בגאומטריה קוראים לשני משולשים עם אותן זוויות משולשים דומים והתכונה המרכזית של משולשים דומים הוא שהיחס בין הצלעות המתאימות שלהם הוא קבוע. כלומר, שמתקיים \( \frac{x}{a}=\frac{y}{b}=\frac{z}{c} \).

בואו ניקח שניה את המשוואה \( \frac{x}{a}=\frac{z}{c} \). נכפיל אותה ב-\( a \) ונחלק אותה ב-\( z \) ונקבל \( \frac{x}{z}=\frac{a}{c} \). כלומר, מצד אחד האורך של הצלעות במשולשים הללו שונה, אבל היחס שבין הניצב \( BC \) ובין היתר \( AB \) הוא קבוע, בלי קשר לגודל של המשולש, כל עוד הזוויות הן אותן זויות. היחס הזה מסומן \( \sin\alpha \), מה שצריך לקרוא בתור “סינוס אלפא”.

כלומר, ההגדרה היא זו: \( \sin\alpha=\frac{a}{c} \) כאשר \( a \) היא אורך הניצב שמול הזווית \( \alpha \) במשולש ישר זווית כלשהו שבו יש את הזווית \( \alpha \), ואילו \( c \) הוא אורך היתר של המשולש הזה. באופן דומה מגדירים את קוסינוס אלפא, בתור \( \cos\alpha=\frac{b}{c} \). כלומר: הסינוס מתקבל כאשר מחלקים את אורך הניצב שמול הזווית ביתר; הקוסינוס מתקבל כאשר מחלקים את אורך הניצב שליד הזווית ביתר.

למה זו הגדרה מעניינת? ובכן, נניח שאני נכנס לתוך תותח ומשתגר לי לאוויר ובואו נתעלם לרגע מזוטות כמו כוח הכבידה כך שיוצא שאני טס לי בקו ישר. אחרי שעברתי מרחק של \( r \) מטרים באוויר, אני שואל את עצמי שתי שאלות - מה הגובה שלי? ומה המרחק על פני הקרקע שעברתי, כלומר אם פתאום אני אפול בקו ישר לקרקע, איפה אני אמצא?

ובכן, התשובה לשאלה הזו היא - “תלוי בזווית שבה שיגרו אותך”, ואנחנו יכולים להשתמש בסינוס וקוסינוס כדי להכניס את הזווית לתמונה באופן מדויק. אמרתי ש-\( \sin\alpha=\frac{a}{c} \) ולכן אפשר לכפול ב-\( c \) ולקבל \( a=c\cdot\sin\alpha \) ובדומה \( b=c\cdot\cos\alpha \). ועבור הסיפור שלי, שבו המרחק שעברתי באוויר הוא \( r \), נקבל שאהיה בגובה \( r\sin\alpha \) ובמרחק אופקי \( r\cos\alpha \).

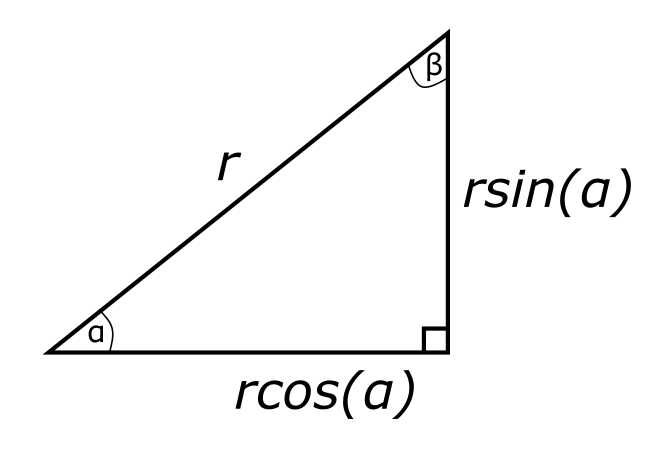
הסיטואציה הזו הייתה זו שבה הבנתי לראשונה את השימושיות של סינוסים וקוסינוסים בעצמי. כלומר, לא בדיוק הסיטואציה שבה משגרים אותי מתותח, אבל הסיטואציה שבה אני יודע את האורך \( r \) של משהו ואני צריך לדעת לפרק אותו לרכיבים - רכיב של “גובה” ורכיב של “מרחק אופקי”. זה היה כשניסיתי לכתוב קוד שמצייר מעגל שרדיוסו הוא \( r \) והייתי צריך למצוא את קואורדינטות ה-\( x,y \) של כל נקודה על המעגל. עוד אחזור לנקודה הזו בהמשך.

בואו ננסה להבין מה ההגדרה שהצגתי יודעת לספר לנו על סינוסים וקוסינוסים.

• הם מוגדרים רק לזוויות בין \( 0^{\circ} \) ו-\( 90^{\circ} \) ולא כולל את שני הקצוות הללו. הסיבה לכך היא שבמשולש סכום המעלות הוא \( 180^{\circ} \) ו-\( 90^{\circ} \) כבר ננגסו על ידי הזווית הישרה, אז \( \alpha+\beta=90^{\circ} \). האבחנה הזו כבר נותנת לנו תחושה לגבי הבעייתיות שבהגדרת סינוס וקוסינוס כך. באופן כללי אלו פונקציות שמוגדרות לכל קלט ולא רק לזוויות מאוד ספציפיות; כלומר, מה שאנחנו רואים עם המשולש הוא רק חלק מהסיפור המלא ועוד אציג את הסיפור המלא בהמשך.
• אינטואטיבית, ככל ש-\( \alpha \) מתקרבת אל \( 0^{\circ} \), כלומר ככל שהיתר נעשה יותר ויותר שטוח, כך הגובה שנגיע אליו מתקרב ל-0 בעצמו. כלומר, האינטואיציה שלנו היא ש-\( \sin0^{\circ}=0 \). עכשיו, כשהיתר יהיה שטוח לגמרי המרחק האופקי שלנו יהיה בדיוק \( r \); כלומר, כדי שזה ישחק יפה עם הנוסחה \( r\cos\alpha \) שראינו עבור המרחק האופי, צריך שיתקיים \( \cos0^{\circ}=1 \). שיקולים דומים יראו לנו שאינטואיטבי שיתקיים \( \sin90^{\circ}=1 \) ו-\( \cos90^{\circ}=0 \). הסימטריה הזו בין סינוס וקוסינוס אינה מקרית ונרחיב עליה בהמשך.
• אחת התכונות המפורסמות ביותר של משולש ישר זווית היא משפט פיתגורס: אם אורכי הניצבים במשולש ישר זווית הם \( a,b \) והיתר הוא \( c \) אז \( a^{2}+b^{2}=c^{2} \). כזכור, ראינו ש-\( a=c\sin\alpha \) ו-\( b=c\cos\alpha \) ולכן אם נציב את אלו במשוואה נקבל \( c^{2}\sin^{2}\alpha+c^{2}\cos^{2}\alpha=c^{2} \). אם נחלק ב-\( c^{2} \) נקבל \( \sin^{2}\alpha+\cos^{2}\alpha=1 \). הנוסחה הזו היא אחת מהנוסחאות הבסיסיות ביותר שקשורות לטריגונומטריה והייתי מצפה שתופיע בדף הנוסחאות שהבאתי למעלה - אבל היא לא! מה שכן, בדף נוסחאות לשלוש יחידות מתמטיקה מצאתי אותה, אבל רק באופן מובלע שכזה:

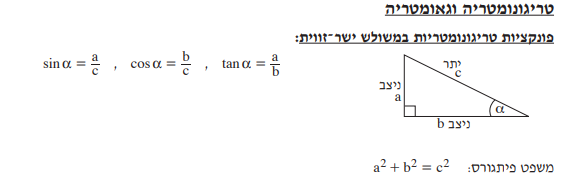
דבר אחד שטרם התייחסתי אליו כלל הוא הזווית הנוספת במשולש שאינה ישרה - הזווית שקראתי לה \( \beta \):

העניין הוא ש-\( \beta \) היא לא זווית עצמאית. כאמור, סכום הזוויות במשולש הוא \( 180^{\circ} \) ולכן \( \alpha+\beta+90^{\circ}=180^{\circ} \), כלומר \( \beta=90^{\circ}-\alpha \). עכשיו, הצלע שמול \( \beta \) היא הצלע שאורכה \( b \), ולכן מאותה הגדרה של סינוס נקבל \( \sin\beta=\frac{b}{c} \). כזכור, הגדרנו גם \( \cos\alpha=\frac{b}{c} \) כך שקיבלנו \( \sin\beta=\cos\alpha \), ואם נציב חזרה את הנוסחה שמצאנו: \( \cos\alpha=\sin\left(90^{\circ}-\alpha\right) \).

באותו אופן, \( \cos\beta=\frac{a}{c} \) יוביל אותנו אל הנוסחה \( \sin\alpha=\cos\left(90^{\circ}-\alpha\right) \). בואו נכתוב אותן במפורש:

• \( \sin\alpha=\cos\left(90^{\circ}-\alpha\right) \)
• \( \cos\alpha=\sin\left(90^{\circ}-\alpha\right) \)

מה הנוסחאות הללו אומרות? ובכן, שאפשר לחשוב על קוסינוס בתור סוג של “סינוס מורצת אחורה”. כשאנחנו ב-\( \alpha=0 \) אז \( \cos\alpha \) נמצאת באותו מקום שבו \( \sin90^{\circ} \) נמצאת ואז כשמגדילים את \( \alpha \) אפשר לראות ש-\( \cos\alpha \) עושה מין הרצה ברברס של מה ש-\( \sin\alpha \) עושה כשהיא מתקרבת אל \( 90^{\circ} \). ככה זה נראה:

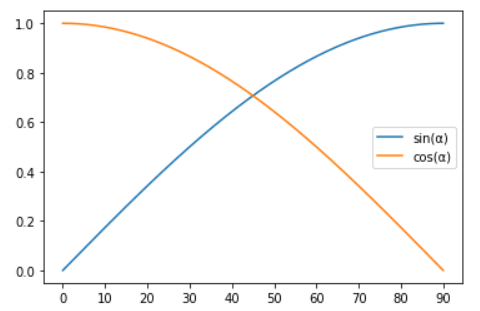
הסימטריה בין הפונקציות ברורה - הקו הצהוב שמייצג קוסינוס הוא תמונת ראי של הקו הצהוב שמייצג סינוס. אבל חייבים להודות ששתי הפונקציות לא נראות מרשימות או מעניינות במיוחד. הן סתם… קו כזה?

אז בואו נעבור להגדרה כללית יותר של סינוס וקוסינוס שמאפשרת לנו לתאר אותם לכל זווית אפשרית, לא רק בין \( 0^{\circ} \) ו-\( 90^{\circ} \). אני כבר אגלה שמה שיתגלה הוא שה”סתם קו כזה” הוא בעצם כל מה שיש - כל מה שנראה בהמשך הוא כל מני הזזות ושיקופים נוספים של הקו הזה, כך שיוצא שהוא בעצם אחד מהקווים החשובים במתמטיקה.

איך מגדירים באופן כללי סינוסים וקוסינוסים?

אני ארצה להגדיר סינוס וקוסינוס באופן כללי בעזרת מעגל היחידה, שזה השם המפוצץ שנותנים למעגל שהרדיוס שלו הוא מאורך 1 (זו ה”יחידה”) והמרכז שלו הוא ראשית הצירים, כלומר נקודה שהקואורדינטות שלה הן \( 0,0 \):

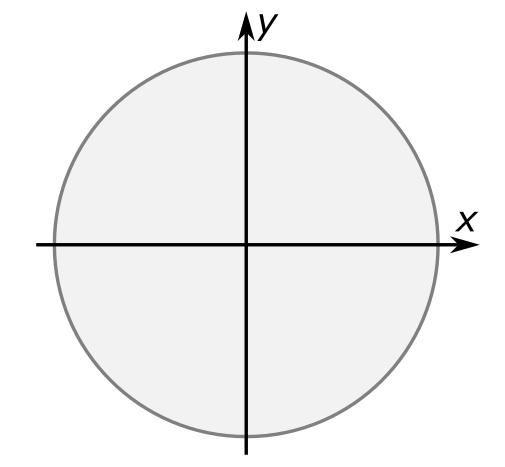
ה”צירים” המדוברים הם הקווים המאונכים שנפגשים במרכז המעגל. לקו האופקי קוראים “ציר \( x \)” ולאנכי “ציר \( y \)”.

עכשיו, בואו ניקח רדיוס כלשהו של המעגל - כלומר, קו ישר ממרכז המעגל אל המעגל עצמו (ב”המעגל” אני מתכוון רק לשפה של העיגול האפור):

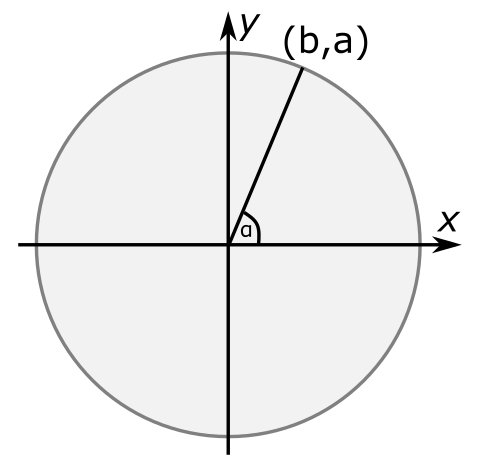
אני מסמן ב-\( \left(b,a\right) \) את הקואורדינטות של הנקודה על המעגל שאליה הרדיוס מגיע (למה לא \( \left(a,b\right) \)? תכף נראה), וב-\( \alpha \) את הזווית שהרדיוס הזה יוצר עם הקו האופקי של ציר \( x \) - ליתר דיוק, עם מה שנקרא הכיוון החיובי של ציר \( x \), שבאיור שלי (ובכל יתר האיורים במתמטיקה, כי זו המוסכמה המקובלת…) פונה לכיוון צד ימין.

עכשיו אפשר להגדיר סינוסים וקוסינוסים באופן כללי:

• \( \sin\alpha=a \)
• \( \cos\alpha=b \)

אבל רגע, מה זה בעצם קואורדינטות? ובכן, לכל נקודה במישור יש קואורדינטה \( \left(b,a\right) \) שאומרת כמה צריך לזוז בכיוון ימינה/שמאלה (זה \( b \)) וכמה צריך לזוז בכיוון למעלה/למטה (זה \( a \)) כדי להגיע אל הנקודה. כדי לראות את זה אוסיף עוד קווים לאיור:

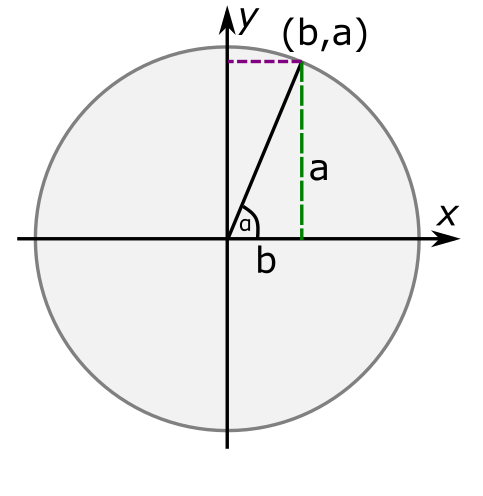
הקו הירוק המקווקו הוא מה שצריך ללכת “למעלה” כדי להגיע אל הנקודה, אם אנחנו נמצאים על ציר \( x \). הקו הסגול הוא כמה צריך ללכת “ימינה”. האורך של הקו הירוק הוא \( a \) והאורך של הקו הסגול הוא \( b \). שימו לב שהקו הסגול והירוק, יחד עם החלקים המתאימים מצירים \( x,y \), מייצרים מלבן; צלעות נגדיות במלבן הן שוות בגודלן, אז אפשר לסמן ב-\( b \) גם את החלק מציר \( x \) למטה שמתחיל בראשית הצירים ומסתיים בתחילת הקו הירוק. ועכשיו, מה קיבלנו? בדיוק את המשולש ישר הזווית שעבורו הגדרנו סינוס וקוסינוס קודם; אנחנו רואים שבמקרה הזה, ההגדרה ה”חדשה” אכן מכלילה את ההגדרה הקודמת.

אבל נו, מה הרווחנו מכל הסיבוך הזה אם בסך הכל קיבלתי את ההגדרה הקודמת? ובכן, בואו ניקח את זה צעד אחד קדימה ניקח את הרדיוס שלנו ונסובב אותו קצת נגד כיוון השעון עד אשר יגיע אל הרביע השמאלי-עליון של המעגל:

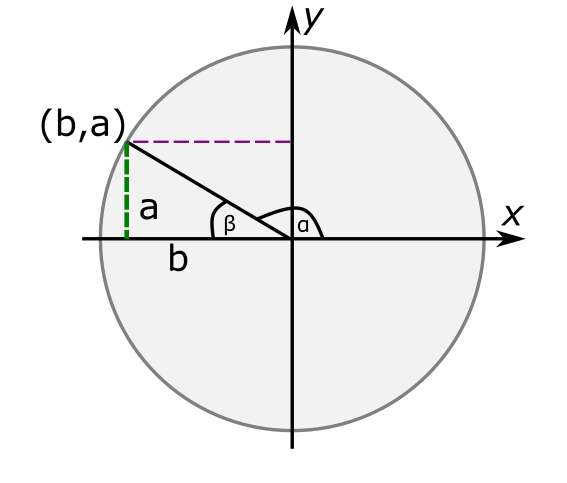
מה קורה פה? לכאורה הגעתי למשהו שנראה כמו תמונת ראי של הסיטואציה הקודמת וציירתי משולש גם בה, אבל שימו לב שהזווית בתוך המשולש, שאני מסמן ב-\( \beta \), אינה הזווית שמעניינת אותנו כאן אלא הזווית ה”מתוחה” שאני מסמן ב-\( \alpha \). זכרו את ההגדרה שנתתי: אני לוקח את הזווית שנוצרת בין הרדיוס ובין הכיוון החיובי של ציר \( x \). כלומר, את כמות הסיבוב שנדרשת כדי להביא את הרדיוס למקומו הנוכחי, אם הוא מתחיל כשהוא מונח על הכיוון החיובי של ציר \( x \) ומתחיל להסתובב נגד כיוון השעון.

אם כן, גם בתמונה הזו \( \sin\alpha=a \) ו-\( \cos\alpha=b \), ואנחנו רואים איך ההגדרה שלנו מטפלת גם במקרים שלא נופלים בין \( 0^{\circ} \) ו-\( 90^{\circ} \). אבל למעשה, אנחנו רואים יותר מכך. מכיוון שהזוויות \( \alpha,\beta \) ביחד מייצגות בדיוק חצי סיבוב (כמות הסיבוב שנדרשת כדי להביא את הרדיוס מהכיוון החיובי של ציר \( x \) אל הכיוון השלילי שלו) הרי ש-\( \alpha+\beta=180^{\circ} \). עכשיו, אם מסתכלים על המשולש ישר הזווית ומשתמשים בהגדרה הקודמת שלנו של סינוס וקוסינוס, מקבלים ש-\( \sin\beta=a \) ולכן קיבלנו את המשוואה

• \( \sin\left(180^{\circ}-\alpha\right)=\sin\alpha \)

זו משוואה שמספרת לנו על סימטריה של הפונקציה \( \sin \) עצמה, ביחס לנקודה של \( 90^{\circ} \). כלומר, שמתקיים \( \sin\left(90^{\circ}+x\right)=\sin\left(90^{\circ}-x\right) \). למה זה נכון? ובכן, אם נסמן \( \alpha=90^{\circ}+x \) אז \( \sin\left(90^{\circ}+x\right)=\sin\alpha=\sin\left(180^{\circ}-\alpha\right)=\sin\left(90^{\circ}-x\right) \). עכשיו, ראינו קודם ש-\( \sin\left(90^{\circ}-x\right)=\cos x \), כלומר קיבלנו ש-\( \sin\left(90^{\circ}+x\right)=\cos x \), ובמילים אחרות - אחרי שסינוס מגיעה אל קו ה-90 מעלות היא מתחילה להתנהג כמו קוסינוס. בהמשך נראה שזה כך באופן כללי - קוסינוס הוא בעצם סינוס עם “הזזה” של \( 90^{\circ} \) קדימה בזמן. תכף נראה איך כל זה מתבטא בגרף של \( \sin \), אבל קודם כל בואו נראה מה קורה עם קוסינוס. וזה יהיה קצת יותר טריקי.

מפתה לומר ש-\( \cos\beta=b \) כי זה מתאים למה שראינו קודם, אבל זה פשוט לא נכון, מהטעם הפשוט ש-\( b \) כאן הוא מספר שלילי, אבל ההגדרה הקודמת שלנו של קוסינוס, שהתבססה על משולש ובה אנחנו מנסים להשתמש עבור \( \cos\beta \), דיברה על האורך של הצלעות. האורך של הצלע שליד \( \beta \) הוא לא \( b \); הוא \( \left|b\right| \) ומכיוון ש-\( b \) שלילי אפשר גם לומר שהוא \( -b \). כלומר, אנחנו מקבלים

• \( \cos\left(180^{\circ}-\alpha\right)=-\cos\alpha \)
• זה הופך את קוסינוס לפונקציה אנטי-סימטרית ביחס לנקודה \( 90^{\circ} \), כלומר \( \cos\left(90^{\circ}+x\right)=-\cos\left(90^{\circ}-x\right)=-\sin x \). בואו נראה איך זה נראה בגרפים:

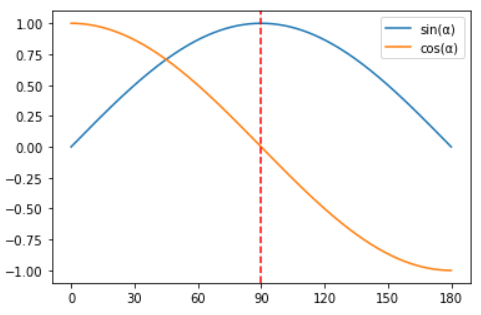
העברתי קו מקווקו אדום בדיוק ב-\( 90^{\circ} \) ואפשר לראות איך הקו הכחול סימטרי ביחס אליו (כלומר, כל צד נראה כמו תמונת ראי של השני) בעוד הקו הצהוב אנטי-סימטרי (כלומר, כל צד נראה כמו תמונת ראי ששוקפה עוד פעם, הפעם ביחס לציר \( x \), של השני), אבל יותר מעניין עכשיו הדמיון בין הקווים עצמם. שימו לב לאופן שבו הקו הכחול, של הסינוס, יורד בין \( 90^{\circ} \) ל-\( 180^{\circ} \); לכו שמאלה לחלק שבין \( 0^{\circ} \) ו-\( 90^{\circ} \) ותראו שהקו הצהוב (של קוסינוס) נראה אותו דבר בדיוק. לעומת זאת לקו הצהוב של הקוסינוס היורד בין \( 90^{\circ} \) ו-\( 180^{\circ} \) עדיין אין מקבילה מדויק, אבל הוא בבירור נראה כמו שיקוף של הקו הכחול שבין \( 0^{\circ} \) ו-\( 90^{\circ} \)- שיקוף ביחס לציר \( x \) (שלא ציירתי כאן במפורש; הקו האופקי שעובר דרך \( y=0 \)).

השלב הבא הוא להבין איך נראות הפונקציות \( \sin\left(180^{\circ}+x\right) \) ו-\( \cos\left(180^{\circ}+x\right) \) עבור ערכי \( x \) מ-\( 0^{\circ} \) עד \( 90^{\circ} \). בשביל זה נמשיך לסובב את הרדיוס שלנו עד שיגיע אל הרביע השלישי, השמאלי-תחתון:

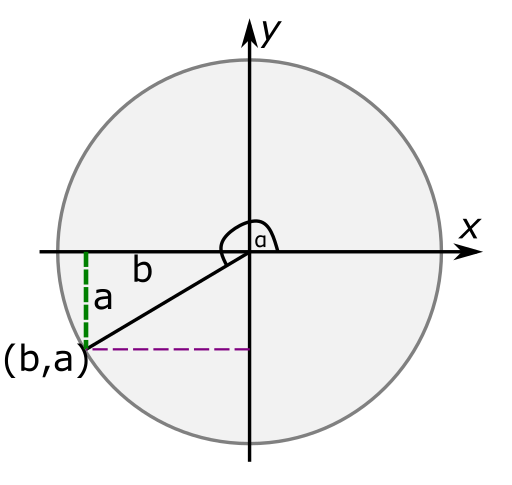
עכשיו אפשר לראות ש-\( \alpha \) מורכבת מזווית של \( 180^{\circ} \) ועוד קצת, כשהקצת מתאר את הסיבוב ברביע השלישי והוא הזווית שמול \( a \) במשולש שציירתי. במילים אחרות, אם \( \alpha=180^{\circ}+x \) אנחנו רואים שמתקיים

\( \sin\left(180^{\circ}+x\right)=-\sin x \)

\( \cos\left(180^{\circ}+x\right)=-\cos x \)

כאשר המינוס בשני המקרים נובע ממה שהסברתי קודם - ערכי הנקודה \( \left(b,a\right) \) שניהם שליליים, אבל \( \sin x,\cos x \) שווים לאורך של הקטעים המתאימים במשולש, כלומר לערכים המוחלטים של \( a,b \).

אם נצייר את הגרף שמתקבל, זה מה שנראה:

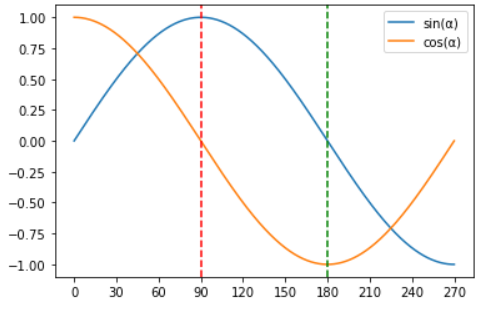
כאן הקו הירוק (הקו המקווקו הימני) מתאר את תחילת החלק שדיברתי עליו. אם מסתכלים על העקום הכחול, של סינוס, רואים שהוא מתחיל את החלק הזה בגובה 0, בדיוק כמו שסינוס התחיל ב-\( 0^{\circ} \), אבל בעוד שהסינוס של \( 0^{\circ} \) עולה למעלה עד 1, הסינוס של \( 180^{\circ} \) יורד למטה, עד \( -1 \), כפי שתיארתי. דבר דומה קורה עם הקוסינוס, רק שהוא עולה כי הקוסינוס של \( 0^{\circ} \) היה בירידה.

כמעט סיימנו! כדי להבין את סינוס וקוסינוס עד הסוף צריך ללוות את הרדיוס שלנו רק עד הרביע האחרון, התחתון-ימני:

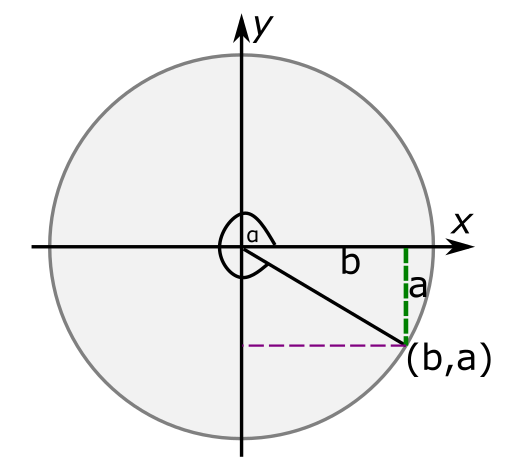
כאן הזווית \( \alpha \) התפתלה כל כך הרבה שהיא כבר נראית כמו פקמן. הפעם הזווית הפנימית בתוך המשולש היא מה שנדרש כדי להשלים סיבוב מלא של \( 360^{\circ} \) יחד עם \( \alpha \), כלומר היא שווה ל-\( 360^{\circ}-\alpha \). כמו כן הפעם \( b \) הוא חיובי ורק \( a \) שלילי. לכן נקבל:

• \( \sin\left(360^{\circ}-\alpha\right)=-\sin\alpha \)
• \( \cos\left(360^{\circ}-\alpha\right)=\cos\alpha \)

אם נציב \( \alpha=270^{\circ}+x \), נקבל ש-\( 360^{\circ}-\alpha=90^{\circ}-x \) ומכאן:

\( \sin\left(270^{\circ}+x\right)=-\sin\left(90^{\circ}-x\right)=-\cos x \)

\( \cos\left(270^{\circ}+x\right)=\cos\left(90^{\circ}-x\right)=\sin x \)

כלומר, החלק הזה של הסינוס מתנהג כמו שקוסינוס התנהג בין \( 0^{\circ} \) ו-\( 90^{\circ} \), רק עולה במקום לרדת, בעוד שהקוסינוס עולה בדיוק כמו שסינוס עלה בין \( 0^{\circ} \) ו-\( 90^{\circ} \):

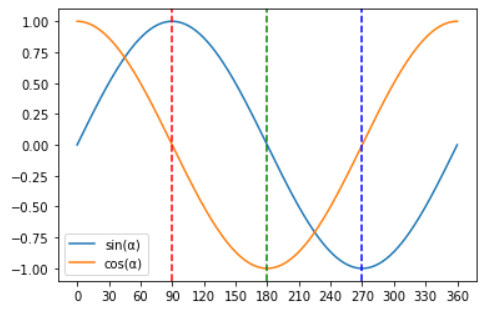
בגרף הזה כבר קל לראות בעיניים את האופן שבו הקו הכחול של הסינוס נראה בדיוק אותו דבר כמו הקו הצהוב של הקוסינוס, למעט זה שהקו של הקוסינוס מקדים אותו ב-\( 90^{\circ} \) - כלומר, אם ניקח את הקו הצהוב ונזיז את כולו \( 90^{\circ} \) ימינה, נקבל בדיוק את הקו הכחול.

עוד דבר שאפשר לראות בגרף הוא שכל הקווים שמופיעים בו הם בעצם הקו של סינוס מהקטע בין \( 0^{\circ} \) ו-\( 90^{\circ} \) - רק כשלוקחים את הקו הזה, משקפים אותו ומזיזים אותו. אני מקווה שעכשיו זה לא כזה מפתיע, פשוט כי ראינו שסינוס וקוסינוס הוגדרו שניהם בעזרת תנועה על מעגל היחידה, ומעגל היחידה הוא סימטרי. כל רביע שלו נראה בדיוק אותו דבר עד כדי שיקופים וסיבובים, לכן הגיוני שהפונקציות “יתנהגו דומה”.

הנקודה האחרונה, והקריטית ביותר לענייננו, היא שסינוס וקוסינוס מסיימים את הגרף הזה, עם ההגעה ל-\( 360^{\circ} \), בדיוק במקום שבו הם התחילו כשהיו ב-\( 0^{\circ} \): סינוס ב-0 וקוסינוס ב-1. זה כמובן לא מקרי - אחרי שסיימנו להשלים סיבוב שלם סביב מעגל היחידה, חזרנו אל נקודת ההתחלה. אבל זה גם אומר שהפונקציות הללו הן מחזוריות: אם נרצה להפעיל אותן על זווית גדולה מ-\( 360^{\circ} \), האפקט יהיה בדיוק של “נסובב את הרדיוס שלנו כמה סיבובים שלמים ואז את מה שנשאר”. למשל, \( \sin400^{\circ}=\sin\left(360^{\circ}+40^{\circ}\right)=\sin40^{\circ} \). באופן כללי נקבל:

\( \sin\left(k\cdot360^{\circ}+\alpha\right)=\sin\alpha \)

\( \cos\left(k\cdot360^{\circ}+\alpha\right)=\cos\alpha \)

וזאת לכל מספר שלם \( k \). כולל שליליים, כי אפשר לחשוב על זווית שלילית פשוט בתור סיבוב של הרדיוס עם כיוון השעון במקום נגדו. ככה זה הולך להיראות (השארתי את הקווים המקווקווים כדי שנקבל תחושה של איפה כל מה שדיברנו עליו עד כה נמצא ביחס לתמונה הגדולה):

כאן המחזוריות של הפונקציות, כמו גם העובדה שקוסינוס זה “סינוס מוזז קצת”, כבר ברורה מאוד לעין, ואני מקווה שגם ברור מה קורה בחלקים האינדיבידואליים של הפונקציות. זה סוגר את השאלה הבסיסית של “מה אלו הפונקציות הללו בכלל?” אבל הסיפור רק מתחיל כאן - עדיין אין לי הסבר לכל הנוסחאות המפחידות שאיתן פתחתי. לכך נגיע בפעם הבאה.