מה בעצם הולך בטריגונומטריה בתיכון? (חלק ב’)

מבוא

בפוסט הקודם שלי על טריגונומטריה הצגתי את הפונקציות \( \sin,\cos \) ונתתי הגדרה שלהן לכל זווית אפשרית. הרעיון הבסיסי היה שהן מספרות לנו מה הקואורדינטות של נקודה שנמצאת על מעגל היחידה שאליה מגיעים על ידי כך שמתחילים עם רדיוס שנח במאוזן על הכיוון החיובי של ציר \( x \), ומתחילים לסובב אותו ורואים עד לאן מגיעים.

הגדרה זה טוב ויפה, אבל בסופו של דבר המטרה שלי היא להבין איך פותרים תרגילים בטריגונומטריה, ולצורך כך צריך קודם כל להבין את דף הנוסחאות המזעזע שפתחתי איתו את הפוסט הקודם:

מה שיעניין אותי עכשיו הוא הנוסחאות

\( \sin\left(\alpha\pm\beta\right)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta \)
\( \cos\left(\alpha\pm\beta\right)=\cos\alpha\cos\beta\mp\cos\alpha\cos\beta \)

מה הנוסחאות הללו אומרות? איך מגיעים אליהן? מהשאלות הללו אני רוצה להתחיל, אבל כאן אני נקלע לדיסוננס חריף מאוד בין גדי תלמיד התיכון ובין גדי שלמד באוניברסיטה. גדי של התיכון מכיר סינוסים וקוסינוסים רק מנקודת המבט הגאומטרית שהצגתי בפוסט הקודם. מנקודת המבט הזו, לא יעזור כלום - ההוכחה של הנוסחאות הללו היא קשה יחסית (למרות שנעשה אותה פה באופן מלא; היא רחוקה מלהיות סוף העולם) וקשה לקבל ממנה אינטואיציה או לזכור את הנוסחאות. אבל באוניברסיטה רואים דרך שונה לגמרי להגיע אל הנוסחאות הללו; דרך שהיא הרבה יותר פשוטה, והופכת את הנוסחאות כמעט לטריוויאליות לשינון. המחיר הוא שהדרך הזו מתבססת על הגדרה מסויימת שאני בהחלט הולך לתת בפוסט הזה, אבל בלי רקע מתמטי מתאים עשויה להיראות כמו רמאות גמורה. אז ברשותכם, אני אתחיל עם הגאומטריה דווקא, ואז אגיע אל הדרך האחרת.

בדרך הגאומטרית אני אצטרך להוכיח רק אחת מארבע הנוסחאות, את \( \sin\left(\alpha+\beta\right)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \); אחר כך אני אראה איך מהנוסחה הזו אפשר לקבל יחסית בקלות את היתר.

הוכחה גאומטרית

נתחיל, אם כן, עם משולש:

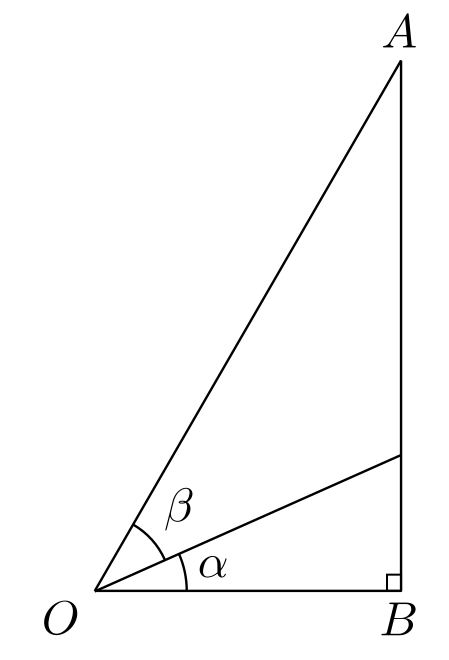
המשולש \( OAB \) הוא ישר זווית (ספציפית, \( \angle OBA=90^{\circ} \)). השימוש ב-\( O \) בתור אחד הקודקודים בא לרמז שאני מצייר את המשולש הזה על מעגל היחידה ש-\( O \) הוא המרכז שלו, ו-\( A \) היא הנקודה שעל המעגל עצמו; \( OA \) הוא היתר של המשולש ומכיוון שאני מתבסס על מעגל היחידה אני מניח ש-\( \left|OA\right|=1 \). בהינתן אלו, \( \sin\left(\alpha+\beta\right)=\left|AB\right| \), כך שצריך לחשב את אורך הצלע \( AB \). לשם כך אני אעזר בקו שפיצל את הזווית במשולש לסכום \( \alpha+\beta \). הרעיון הוא לקחת את הקו הזה ולהמשיך אותו גם מעבר למשולש, עד שהוא יהיה ארוך מספיק כדי שאוכל להוריד אליו אנך מנקודה \( A \). ככה זה נראה:

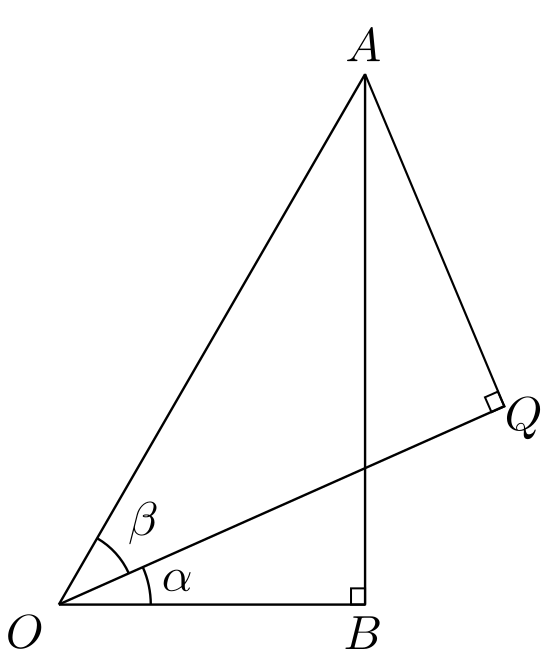
המשמעות של “אנך” היא שהקו \( AQ \) שיורד אל \( OQ \) פוגש אותו בזווית של 90 מעלות, כלומר \( \angle OQA=90^{\circ} \). התעלול הזה של “להוריד אנך מנקודה לקו קיים” הוא אחד מהשימושיים ביותר כשפותרים תרגילים בגאומטריה כי אנכים עושים כל מני דברים נחמדים. כמובן, אפשר לשאול ובצד איך בכלל אפשר להוריד אנך. אני סתם ציירתי קו מ-\( A \) שנראה לי בערך מאונך (ואז כשניסיתי לצייר את הריבוע הקטן של הזווית הישרה ראיתי שיצא לי עקום לגמרי ותיקנתי) אבל כבר אוקלידס עסק בפתרון פורמלי יותר לשאלה הזו. ב”יסודות” של אוקלידס, בטענה 11, מגיע הסבר איך ליצור אנך כזה - הרעיון הוא להשתמש במחוגה, אחד משני כלי העבודה הבסיסיים שאוקלידס עובד איתם (השני הוא סרגל לא מסומן). כשהייתי בתיכון השימוש היחיד למחוגה אצלי היה לזנק מן הקלמר ולפצוע אותי באצבע - באמת, הייתה לי טראומה מהמכשיר הזה.

בואו נסתכל לרגע על המשולש \( OQA \) שקיבלנו. זה משולש ישר זווית, והיתר שלו הוא \( AO \) שכבר אמרתי שאני אוהב כי \( \left|AO\right|=1 \). במילים אחרות, אחרי שהתחלנו עם משולש ישר זווית ש-\( AO \) הייתה היתר שלו, עכשיו בנינו עוד משולש ישר זווית ש-\( AO \) היא היתר שלו, אבל הזוויות שלו שונות: במקום שתהיה בו הזווית \( \alpha+\beta \) יש בו את הזווית \( \beta \) לבדה. בפרט, \( \left|AQ\right|=\sin\beta \) ו-\( \left|OQ\right|=\cos\beta \). זה מקדם אותנו משמעותית - אורכי שתי הצלעות הללו הן חצי מ”נתוני הבסיס” שאנחנו מצפים לקבל את התוצאה שלנו באמצעותם. רק צריך איכשהו להכניס את \( \alpha \) לתמונה גם כן.

העניין הוא ש-\( \alpha \) כבר בתמונה ופשוט לא שמנו לב. בואו נסתכל לרגע על הנקודה שבה נחתכים \( AB \) ו-\( OQ \), שלא נתתי לה שם כדי לא לסרבל יותר מדי:

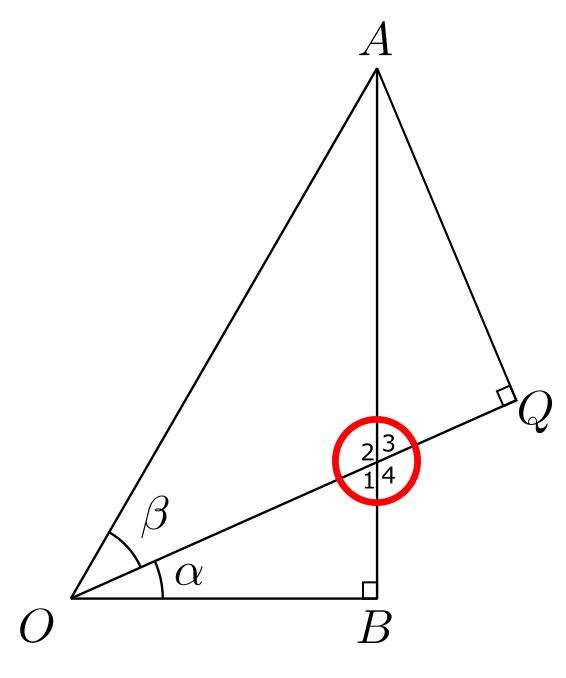
סביב הנקודה הזו יש ארבע זוויות שסימנתי ב-1,2,3,4. כל צמד זוויות שלא נוגעות זו בזו נקראות זוויות קודקודיות (כי יש להן רק קודקוד משותף). כאן 1 ו-3 הן הזוויות הקודקודיות שיעניינו אותי. מה שיפה בזוויות קודקודיות הוא שהן תמיד שוות זו לזו. כדי לראות את זה, שימו לב שהזוויות 1 ו-2 משלימות ביחד חצי סיבוב בדיוק, על הצד השמאלי של הישר \( AB \). כלומר, אם אני מסמן אותן בתור \( \gamma_{1},\gamma_{2} \) אז \( \gamma_{1}+\gamma_{2}=180^{\circ} \) כי חצי סיבוב הוא בדיוק 180 מעלות. עכשיו, גם הזוויות 2,3 משלימות חצי סיבוב בדיוק, על הצד העליון של \( OQ \) ולכן \( \gamma_{3}+\gamma_{2}=180^{\circ}=\gamma_{1}+\gamma_{2} \) ואחרי חיסור \( \alpha_{2} \) משני האגפים נקבל \( \gamma_{1}=\gamma_{3} \). אין כאן קסם שייחודי לבניה הספציפית הזו; זו תוצאה כללית בגאומטריה.

עכשיו, הזווית \( \gamma_{1} \) הזו משתתפת במשולש התחתון יחד עם הזווית הישרה \( \angle ABO \) והזווית \( \angle BOQ \) ששווה ל-\( \alpha \) המקורי שלנו. המסקנה היא ש-\( \gamma_{1}=90^{\circ}-\alpha \) (כי סכום הזוויות במשולש הוא \( 180^{\circ} \)). לכן גם \( \gamma_{3} \) שווה ואז נקבל שהזווית \( \angle BAQ \) העליונה שווה גם ל-\( \alpha \) שזה בעצם מה שרציתי להראות בכל הטררם הנוכחי.

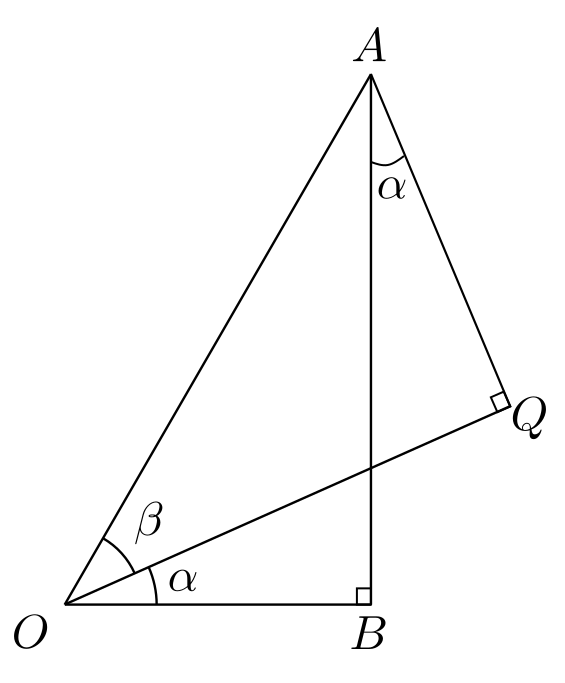
אנחנו די קרובים לסיום למרות שזה עדיין ממש לא נראה כך - עדיין נדרשות ממני כמה בניות עזר. נתחיל עם \( OQ \). כבר חישבנו קודם ש-\( \left|OQ\right|=\cos\beta \), ועכשיו אני רוצה לנצל את זה. לצורך כך בואו נשים לב לכך שאם רק נוריד אנך מ-\( Q \) אל ההמשך של הישר שעובר דרך \( OB \) נקבל משולש ישר זווית ש-\( OQ \) הוא היתר שלו:

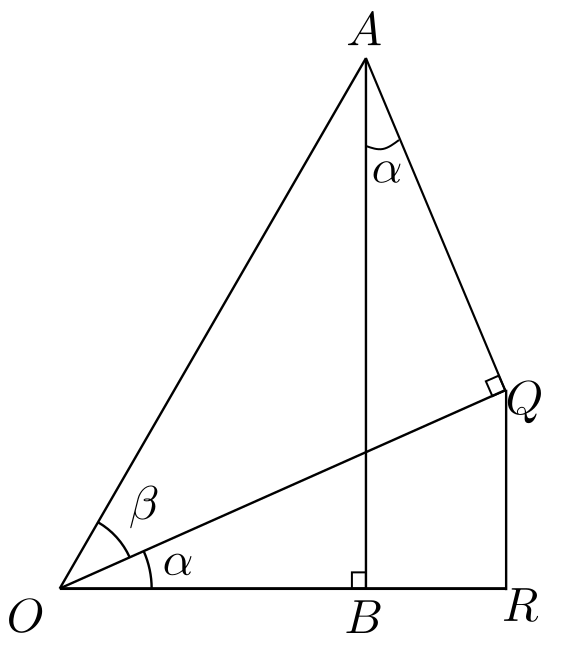
במשולש החדש הזה מתקיים \( \frac{\left|RQ\right|}{\left|OQ\right|}=\sin\alpha \) פשוט על פי הגדרת סינוס. לכן, אם נשתמש ב-\( \left|OQ\right|=\cos\beta \), נקבל \( \left|RQ\right|=\sin\alpha\cos\beta \). הופה! זה דבר רציני ביותר - קיבלנו כבר את אחד משני הביטויים שמשתתפים בסכום הסופי, והבנו מאיפה צצה המכפלה הזו של סינוס של זווית אחת בקוסינוס של הזווית השניה. אבל איך אפשר לקשר את \( RQ \) הזה שהוא קטע חדש שהוספנו משום מקום, אל מה שאנחנו רוצים לחשב, שהוא כזכור האורך של \( AB \)? ובכן, אפשר להיעזר בכך שגם \( AB \) וגם \( RQ \) שניהם מאונכים מ-\( OR \) כדי לבנות מלבן שמערב אותם:

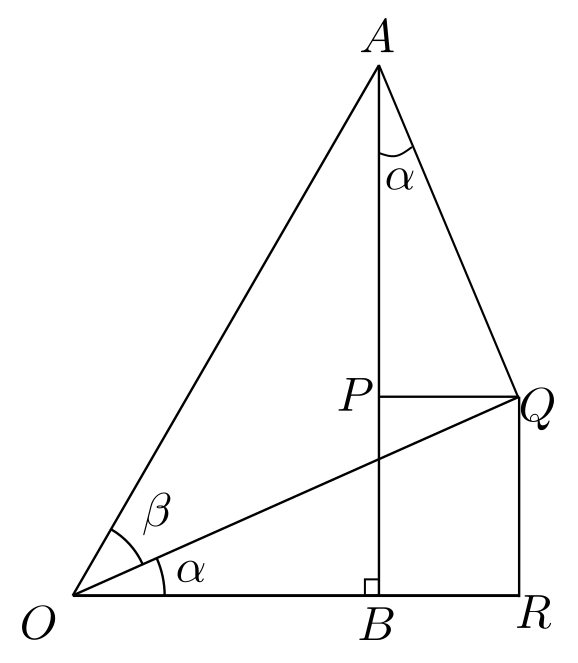
במלבן \( PQRB \), שהתקבל על ידי הורדת אנך מ-\( Q \) אל \( AB \), אנחנו יודעים שהצלע \( QR \) שווה באורכה לצלע \( PB \), כלומר \( \left|PB\right|=\sin\alpha\cos\beta \). כדי לסיים את ההוכחה צריך לחשב את האורך של \( AP \), כי \( \left|AB\right|=\left|AP\right|+\left|PB\right| \). למרבה המזל, זה חישוב קל במיוחד: המשולש \( APQ \) הוא ישר זווית עם יתר \( AQ \) וכבר חישבנו ומצאנו שהזווית \( \angle PAQ \) היא \( \alpha \), ולכן \( \frac{\left|AP\right|}{\left|AQ\right|}=\cos\alpha \). ראינו קודם ש-\( \left|AQ\right|=\sin\beta \), ולכן נקבל ש-\( \left|AP\right|=\cos\alpha\sin\beta \). בזאת סיימנו:

יפה מאוד! האם אפשר לנוח כעת על זרי הדפנה? ובכן, לא.

מה יצא לנו מההוכחה הגאומטרית?

למה עוד לא סיימנו? ראשית, הבטחתי דרך טובה יותר לזכור את הנוסחה הזו מאשר שינון ההוכחה הזו, שאמנם התחלתי לחבב תוך כדי כתיבת הפוסט אבל היא עדיין לא בדיוק משהו שקל לזכור. אבל שנית, וחמור יותר, ההוכחה הזו התבססה על משולשים, כלומר הניחה במובלע שהזוויות \( \alpha,\beta \) גם יחד הן קטנות מספיק - סכומן לא עולה על 90 מעלות. העניין הוא שראינו בפוסט הקודם שסינוס וקוסינוס הם בעצם רק מה שקורה בטווח המעלות הזה; כל מה שקורה מחוץ לטווח המעלות מתקבל בצורה כלשהי מהפונקציה בתוך טווח המעלות הזה (אולי עם שיקוף כלשהו). לכן אני אוותר על החלוקה למקרים הפדנטית שנדרשת כדי להוכיח שאפשר להיעזר בתוצאה הזו כדי להוכיח את התוצאה הכללית ביותר.

בכל זאת, אי אפשר בלי דוגמא כלשהי כדי שנשתכנע שאין פה רמאות גמורה. בואו נניח אם כן ש-\( \alpha,\beta \) הן זוויות בטווח הנכון של בין \( 0^{\circ} \) ל-\( 90^{\circ} \) אבל הסכום שלהן גדול מ-\( 90^{\circ} \), כלומר \( 90^{\circ}\le\alpha+\beta\le180^{\circ} \). כעת, נזכור שראינו בפוסט הקודם ש-

\( \sin\left(180^{\circ}-\gamma\right)=\sin\gamma \)

כלומר, במקרה שלנו:

\( \sin\left(\alpha+\beta\right)=\sin\left(180^{\circ}-\left(\alpha+\beta\right)\right)=\sin\left(\left(90^{\circ}-\alpha\right)+\left(90^{\circ}-\beta\right)\right) \)

עכשיו, \( \left(90^{\circ}-\alpha\right) \) ו-\( \left(90^{\circ}-\beta\right) \) הן שתיהן זוויות ש:

נמצאות בטווח שבין \( 0^{\circ} \) ובין \( 90^{\circ} \)
סכומן לא עולה על \( 90^{\circ} \) (כי סכומן הוא \( 180^{\circ}-\left(\alpha+\beta\right) \) שהוא קטן מ-\( 90^{\circ} \) כי \( \left(\alpha+\beta\right) \) גדול מ-\( 90^{\circ} \))

לכן התוצאה שהוכחנו זה עתה עובדת עבור הזוויות הללו, ונקבל:

\( \sin\left(\alpha+\beta\right)=\sin\left(90^{\circ}-\alpha\right)\cos\left(90^{\circ}-\beta\right)+\sin\left(90^{\circ}-\beta\right)\cos\left(90^{\circ}-\alpha\right) \)

כזכור מהפוסט הקודם, \( \sin\left(90^{\circ}-\alpha\right)=\cos\alpha \) ו-\( \cos\left(90^{\circ}-\alpha\right)=\sin\alpha \), כלומר אגף ימין של המשוואה שלעיל הופך להיות

\( \cos\alpha\sin\beta+\sin\alpha\cos\beta \)

וזה מה שאנחנו רוצים, באופן לא מפתיע. כך זה יעבוד גם בכל מקרה אחר - כאמור, לא אכנס לפרטים הללו.

מה שכן כדאי להרחיב עליו הוא איך מהנוסחה שכבר מצאתי אני מגיע לכל היתר. כזכור, התחלתי עם הנוסחאות הבאות:

\( \sin\left(\alpha\pm\beta\right)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta \)
\( \cos\left(\alpha\pm\beta\right)=\cos\alpha\cos\beta\mp\cos\alpha\cos\beta \)

אלו ארבע נוסחאות שונות, אבל הוכחתי רק אחת מהן - את \( \sin\left(\alpha+\beta\right)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \). לכל היתר אפשר להגיע בקלות בעזרתה אם ניעזר בנוסחאות אחרות שכבר ראינו.

נתחיל עם \( \sin\left(\alpha-\beta\right) \). בעצם, יש לנו כאן חיבור בתחפושת: \( \sin\left(\alpha-\beta\right)=\sin\left(\alpha+\left(-\beta\right)\right) \). כלומר, אם כבר הסכמנו שנוסחת החיבור עובדת לכל זווית, אז היא עובדת גם עבור מינוס של זוויות (מינוס של מספר הוא… מספר). כלומר, אנחנו מקבלים:

\( \sin\left(\alpha-\beta\right)=\sin\left(\alpha+\left(-\beta\right)\right)=\sin\alpha\cos\left(-\beta\right)+\cos\alpha\sin\left(-\beta\right) \)

עכשיו בואו ניזכר איך סינוס וקוסינוס מתמודדים עם מינוס של זווית: לקוסינוס לא אכפת, אבל סינוס מוכפל במינוס:

\( \sin\left(-\beta\right)=-\sin\beta \)

\( \cos\left(-\beta\right)=\cos\beta \)

ולכן נקבל:

\( \sin\alpha\cos\left(-\beta\right)+\cos\alpha\sin\left(-\beta\right)=\sin\alpha\cos\beta-\cos\alpha\sin\beta \)

וזו בדיוק הנוסחה השניה שרצינו.

נעבור עכשיו אל נוסחת הסכום עבור קוסינוס. נתחיל עם תזכורת על האופן שבו סינוס וקוסינוס מחוברים יחד:

\( \sin\left(\alpha\right)=\cos\left(90^{\circ}-\alpha\right) \)

\( \cos\left(\alpha\right)=\sin\left(90^{\circ}-\alpha\right) \)

בואו נשתמש בזה כדי לחשב את \( \cos\left(\alpha+\beta\right) \):

\( \cos\left(\alpha+\beta\right)=\sin\left(90^{\circ}-\left(\alpha+\beta\right)\right)=\sin\left(\left(90^{\circ}-\alpha\right)-\beta\right) \)

כלומר, עברתי לסינוס של הפרש שתי זוויות: אחת היא \( 90^{\circ}-\alpha \) והשניה היא \( \beta \). על זה אפשר להשתמש בנוסחת ההפרש שראינו קודם:

\( \sin\left(\left(90^{\circ}-\alpha\right)-\beta\right)=\sin\left(90^{\circ}-\alpha\right)\cos\beta-\cos\left(90^{\circ}-\alpha\right)\sin\beta \)

ולסיום, אפשר להעלים את ה-90 מעלות על ידי מעבר מסינוס לקוסינוס וההפך:

\( \sin\left(90^{\circ}-\alpha\right)\cos\beta-\cos\left(90^{\circ}-\alpha\right)\sin\beta=\cos\alpha\cos\beta-\sin\alpha\sin\beta \)

וזו בדיוק הנוסחה שרצינו. עבור הפרש קוסינוסים עושים את אותו תעלול של החלפת \( \beta \) ב-\( -\beta \) שעשינו קודם ומקבלים שהמקדם של \( \sin\alpha\sin\beta \) יהפוך לפלוס. זה מסיים את הוכחת ארבע הנוסחאות; כפי שאנחנו רואים, עיקר העבודה הייתה להוכיח את נוסחת החיבור עבור סינוס.

ועכשיו הבה ונעבור למשהו שונה לגמרי.

נוסחת אוילר

אני חושב שהדבר הכי פשוט לעשות עם נוסחת אוילר הוא פשוט להציג אותה ואז להסביר מה הולך פה. אז הנה היא:

\( e^{i\alpha}=\cos\alpha+i\sin\alpha \)

מה יש לנו בנוסחה הזו? ובכן, באגף ימין יש לנו את \( \sin\alpha \) ואת \( \cos\alpha \) שאנחנו כבר מכירים. פרט אליהם יש את האות \( i \). מה האות הזו מייצגת כאן? היא מייצגת מספר שמקיים את התכונה \( i^{2}=-1 \). מספר כזה הוא דוגמא למה שנקרא מספר מרוכב ובהחלט ייתכן שחלק מהקוראים לא מכירים; אבל גם לא צריך להכיר אותו כאן מעבר ל”זה מספר שמקיים \( i^{2}=-1 \) והוא ממש ממש אמיתי ולא סתם איזה שקר שהמצאנו כרגע בבקשה תאמינו לנו” (ולמה בכלל שזה ירגיש כמו שקר? ובכן, כי כל מספר ממשי \( a \) מקיים \( a^{2}\ge0 \) ובפרט אי אפשר לקבל \( -1 \) על ידי העלאה בריבוע של מספר ממשי).

באגף שמאל יש לנו את אותו \( i \) ואת הזווית \( \alpha \) כשהם נמצאים במעריך של חזקה שהבסיס שלה מסומן ב-\( e \). מי זה \( e \)? ובכן, זה לא מספר אקראי; זה מספר חשוב במתמטיקה שהוא בערך \( 2.71828\ldots \). אבל כמו עם \( i \), כך גם כאן; כדי להיעזר בנוסחת אוילר לא צריך לדעת עליו שום דבר מעבר לכך.

בנוסף לכך, כדי שהנוסחה “תעבוד” צריך ש-\( \alpha \) תהיה נתונה לא במעלות אלא במשהו שנקרא רדיאנים, אבל כמו שכבר אמרתי - גם על רדיאנים לא צריך לדעת שום דבר אם אנחנו רק רוצים להיעזר בנוסחת אוילר.

אז הנה שתי שאלות שאני הולך לענות עליהן:

איך נעזרים בנוסחת אוילר בשביל לקבל את נוסחת הסכום?
למה נוסחת אוילר נכונה בכלל?

אני מתחיל עם שאלה 1 כי התשובה ל-2 מאוד מסובכת ולא הכרחית כל עוד סומכים עלי בעיניים עצומות. בשביל 1, צריך להיזכר לרגע איך עובדים חוקי החזקות הרגילים:

\( a^{x}\cdot a^{y}=a^{x+y} \)

במילים אחרות - אם כופלים שתי חזקות עם אותו בסיס, מקבלים חזקה עם הבסיס הזה, שהמעריך שלה הוא סכום המעריכים של החזקות. חזקה הופכת כפל (של הבסיסים) לסכום (של המעריכים). בדומה, היא יכולה גם להפוך סכום (של המעריכים) לכפל (של הבסיסים). אז עכשיו בואו ניקח את נוסחת אוילר ונציב במעריך שלה את הסכום \( \alpha+\beta \):

\( e^{i\left(\alpha+\beta\right)}=\cos\left(\alpha+\beta\right)+i\sin\left(\alpha+\beta\right) \)

אם נצליח למצוא ייצוג יותר נחמד ל-\( e^{i\left(\alpha+\beta\right)} \), זה יניב לנו שתי נוסחאות בבת אחת - גם עבור סינוס של סכום זוויות וגם עבור קוסינוס של סכום זוויות. כדי לראות את זה קורה, בואו נשתמש ב”סכום של מעריכים מתורגם למכפלת הבסיסים”:

\( e^{i\left(\alpha+\beta\right)}=e^{i\alpha}\cdot e^{i\beta}=\left(\cos\alpha+i\sin\alpha\right)\left(\cos\beta+i\sin\beta\right) \)

עכשיו, איך נפתח את מכפלת הסוגריים שמופיעה באגף ימין? כמו שתמיד פותחים מכפלת סוגריים - נקבל ארבעה איברים:

\( \cos\alpha\cos\beta+i\sin\alpha\cos\beta+i\cos\alpha\sin\beta+i^{2}\sin\alpha\sin\beta \)

נשתמש בכך ש-\( i^{2}=-1 \), נקבץ איברים ונקבל:

\( \left(\cos\alpha\cos\beta-\sin\alpha\sin\beta\right)+i\left(\sin\alpha\cos\beta+\cos\alpha\sin\beta\right) \)

עכשיו נשווה את מה שקיבלנו אל הביטוי המקורי:

\( \cos\left(\alpha+\beta\right)+i\sin\left(\alpha+\beta\right) \)

אם נסתכל על האיברים שמוכפלים ב-\( i \) בשני הביטויים ונשווה אותם, נקבל

\( \sin\left(\alpha+\beta\right)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \)

ואם נסתכל על האיברים שלא מוכפלים ב-\( i \) ונשווה אותם, נקבל

\( \cos\left(\alpha+\beta\right)=\cos\alpha\cos\beta-\sin\alpha\sin\beta \)

וזהו, זה מסיים את פיתוח הנוסחאות הללו - בלי לצייר משולשים ובלי שום דבר אחר. והחלק היפה ביותר כאן הוא שזו הוכחה פורמלית לחלוטין אם כבר הוכחנו את נוסחת אוילר. אבל כפי שאמרתי - בשביל הפיתוח הקצרצר שעשיתי כרגע לא צריך לדעת למה נוסחת אוילר נכונה או אפילו להכיר לעומק את הרכיבים שלה. אפשר לחשוב עליה בתור טריק כדי לזכור בקלות את הנוסחאות הטריגונומטריות ותו לא. עם זאת, לטעמי עיקר הכיף פה הוא בדיוק בקלות שבה הכל נובע, וכמה “ברור” מאיפה כל רכיב בנוסחאות הטריגונומטריות מגיע פתאום.

אז למה נוסחת אוילר נכונה?

החלק הזה יהיה מין “חלק בונוס”. אני אזרוק הסברים מטורללים מהשרוול בלי להיכנס לעובי ההוכחות, ובהחלט ייתכן שתאבדו אותי פה; אבל אם נצא מכאן עם מושג כללי לגבי מה הולך פה ועד כמה מתחבאים מתחת לפני השטח של המתמטיקה דברים מגניבים, התקדמנו.

לב העניין הוא בהצגה של פונקציות מסויימות בתור טורי טיילור. טור טיילור הוא סכום אינסופי של מחוברים, ש… למה אני מדבר כל כך הרבה, הנה הטורים:

\( e^{x}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\ldots=\sum_{n=0}^{\infty}\frac{x^{n}}{n!} \)
\( \sin x=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\ldots=\sum_{n=0}^{\infty}\left(-1\right)^{n}\frac{x^{2n+1}}{\left(2n+1\right)!} \)
\( \cos x=1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\ldots=\sum_{n=0}^{\infty}\left(-1\right)^{n}\frac{x^{2n}}{\left(2n\right)!} \)

המשמעות של הטורים הללו היא שככל שנחבר יותר מחוברים, כך נתקרב יותר ויותר לערך ה”אמיתי” של הביטוי באגף שמאל. בגלל שהמכנה של המחוברים הולך וגדל במהירות (כי ככה זו פונקציית עצרת), עבור ערכים לא גדולים של \( x \) לא נזדקק לחיבור של יותר מדי מחוברים. למשל, עבור \( x=3 \) אני יכול לחשב ידנית מה זה \( e^{3} \): מכיוון ש-\( e\approx2.71828 \) אני אקח מחשבון, אכפול את \( 2.71828 \) פעמיים בעצמו ואקבל \( 20.085496391455552 \). עכשיו אני אלך אל הטור \( 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\ldots \), אציב \( x=3 \) ואתחיל לחבר איברים:

\( 1+3+\frac{9}{2}+\frac{27}{6}+\frac{81}{24}+\frac{243}{120}+\frac{729}{720}+\frac{2187}{5040} \)

למה אני עוצר ב-\( \frac{3^{7}}{7!}=\frac{2187}{5040} \)? כי האיבר הבא כבר יהיה די קטן, כי את המונה אני כופל ב-3 אבל את המכנה אני אכפול ב-8 - אני אקבל איבר שהוא פחות מ-\( 0.2 \) ונראה לי שהבנו את הקטע.

אחרי שאני מחבר את כל המספרים הללו אני אקבל \( 20.063392857142855 \) שכבר מאוד קרוב אל המספר שאני מצפה לקבל - ועוד כמה איברים בטור יניבו לי מספרים כמעט זהים. אז הנוסחה באמת עובדת יפה עבור הפונקציה \( e^{x} \).

מה עם \( \sin x \)? ובכן, מדגדג להציב \( x=90^{\circ} \) ולראות איך מקבלים את 1 אבל שום דבר כזה לא יקרה. למעשה, נקבל מספר גדול בצורה מפחידה. מה עשינו לא נכון? ובכן, הנוסחה לעיל לא נכונה עבור סינוס אם אנחנו מודדים את הזוויות במעלות. בשביל שהיא תעבוד, אנחנו חייבים למדוד את הזוויות באמצעות משהו שנקרא רדיאנים. לא כזה חשוב מה ההגדרה המדויקת של רדיאן (כמות הרדיאנים בזווית מסויימת שווה לאורך הקשת של מעגל היחידה שנשענת על הזווית הזו; יש לי פוסט בנושא) אלא איך “מתרגמים” מעלות לרדיאנים. הכלל פשוט מאוד: מחלקים ב-\( 360 \) וכופלים ב-\( 2\pi \), כי 360 מעלות זה היקף מעגל שלם במעלות, ואילו \( 2\pi \) זה היקף מעגל שלם ברדיאנים (אפשר כמובן גם לחלק ב-180 ולכפול ב-\( \pi \); אותו אפקט). אז במקרה שלנו, זווית של תשעים מעלות שווה ל-\( \frac{\pi}{2}\approx1.5708 \) רדיאנים. בואו ננסה להציב את זה בנוסחה:

\( \frac{\pi}{2}-\frac{1}{6}\left(\frac{\pi}{2}\right)^{3}+\frac{1}{120}\left(\frac{\pi}{2}\right)^{5}\approx1.0045 \)

זה… קירוב לא רע בכלל של 1! וזה יילך וישתפר ככל שנחבר עוד איברים. אני אחסוך מאיתנו את הניסוי עבור קוסינוס - זה יעבוד גם שם. כלומר, עוד לפני שמגיעים לנוסחת אוילר כבר יש לנו משהו נחמד מאוד - שיטה פרקטית לחשב את סינוס וקוסינוס בצורה טובה מאוד. כשאני למדתי טריגונומטריה בבית הספר ראיתי המון זהויות טריגונומטריות, אבל שום הסבר על איך אפשר לחשב את הפונקציות הטריגונומטריות בפועל.

כמובן, זו שאלה מצויינת מאיפה הנוסחאות הללו בכלל הגיעו ולמה הן נכונות. התשובה היא שאם מאמצים את ההגדרה שלנו לסינוס וקוסינוס, צריך להשתמש בכלים מחשבון דיפרנציאלי כדי להגיע אל הנוסחאות הללו; ספציפית, צריך לגזור שוב ושוב את הפונקציות ולהשתמש בנוסחה הכללית למציאת טור טיילור של משהו (\( f\left(x-x_{0}\right)\approx\sum_{n=0}^{\infty}f^{\left(n\right)}\left(x_{0}\right)\frac{\left(x-x_{0}\right)^{n}}{n!} \) כאשר \( f^{\left(n\right)} \) מייצג את הנגזרת ה-\( n \)-ית ו-\( x_{0} \) היא נקודה שסביבה בוחרים לפתח את טור הטיילור; במקרה של הטורים למעלה בחרנו \( x_{0}=0 \)). תשובה אחרת, שבמבט ראשון נשמעת מוזרה למדי, היא שרוב מי שרוצים להגדיר פורמלית סינוסים וקוסינוסים מגדירים אותם מלכתחילה בתור הטורים הללו ולא בעזרת הגדרות גאומטריות. יש לכך יתרונות; ההגדרה הזו הרבה יותר פורמלית. אבל כמובן, אי אפשר ללמד הגדרה כזו בבית הספר. אני עצמי בחרתי להציג בבלוג הגדרה לסינוסים וקוסינוסים שהיא סוג של אמצע הדרך בין שתי הגישות - להגדיר אותם בתור פתרונות של משוואה דיפרנציאלית (הנה הפוסט). בצורה הזו נהנים משני העולמות - גם מתבססים על חשבון דיפרנציאלי שלא נגיש בכלל בתיכון וגם נותנים תחושה שמשהו פה לא פורמלי עד הסוף.

נחזור אל טורי הטיילור שלנו. אם נסתכל עליהם קצת נראה שהם מאוד דומים. הטור של \( e^{x} \) מכיל איברים שאחר כך מתפזרים לשתי קבוצות (“החזקות הזוגיות” ו”החזקות האי זוגיות”) ומופיעים אצל קוסינוס (הזוגיות) וסינוס (האי זוגיות), רק ששם יש להן סימן מינוס לפעמים. כלומר, כבר עכשיו אפשר לחשוב שיש פה קשר חזק - נוסחת אוילר זה לא סתם איזו הגדרה אקראית נטולת פשר.

הרעיון הוא לקחת את הנוסחה עבור \( e^{x} \), שבמקור מוכיחים את הנכונות שלה רק עבור ערכי \( x \) ממשיים, ולהציב בה את הערך \( x=i\alpha \), שהוא מספר מרוכב. כרגיל, אני חוסך מכם את ההוכחה הפורמלית שאפשר לעשות את זה (וכרגיל, אני מזהיר אתכם שמתמטיקאים אוהבים להגדיר את הפונקציה \( e^{x} \) ככה מראש גם עבור מרוכבים, מה שהופך את נוסחת אוילר פשוט להגדרה וזה לא משהו שעושה לנו נעים לאינטואיציה גם אם זה נטוע עמוק בתובנות מתמטיות אמיתיות) - בואו פשוט נראה מה קורה.

כזכור, אמרתי ש-\( i \) הוא מספר בעל התכונה ש-\( i^{2}=-1 \). אז מה זה \( i^{3} \)? פשוט מאוד: \( i^{3}=i^{2}\cdot i=-i \). ומה זה \( i^{4} \)? שוב, פשוט מאוד: \( i^{4}=\left(i^{2}\right)^{2}=\left(-1\right)^{2}=1 \). כלומר, אם מסתכלים על חזקות של \( i \) רואים איזו שהיא מחזוריות כאן:

\( i^{0},i^{1},i^{2},i^{3},i^{4},i^{5},i^{6},i^{7},i^{8},\ldots \)

הופך ל

\( 1,i,-1,-i,1,i,-1,-i,1,\ldots \)

זה בדיוק מה שיקרה כשנציב את \( i\alpha \) בטור של האקספוננט. חצי מהמחוברים יהיו מהצורה “\( i \) כפול משהו” והחצי השני מהצורה “1 כפול משהו”, כשהמשהו מזפזפ בין להיות בלי מינוס ולהיות עם מינוס:

\( e^{i\alpha}=1+\left(i\alpha\right)+\frac{\left(i\alpha\right)^{2}}{2!}+\frac{\left(i\alpha\right)^{3}}{3!}+\frac{\left(i\alpha\right)^{4}}{4!}+\ldots \)

\( =1+i\alpha-\frac{\alpha^{2}}{2!}-i\frac{\alpha^{3}}{3!}+\frac{\alpha^{4}}{4!}+\ldots \)

את הטור הזה אפשר “לפצל לשניים” (שוב, זה דורש הוכחה):

\( 1+i\alpha-\frac{\alpha^{2}}{2!}-i\frac{\alpha^{3}}{3!}+\frac{\alpha^{4}}{4!}+\ldots=\left(1-\frac{\alpha^{2}}{2!}+\frac{\alpha^{4}}{4!}+\ldots\right)+i\left(\alpha-\frac{\alpha^{3}}{3!}+\ldots\right) \)

וקיבלנו את שני הטורים עבור סינוס וקוסינוס:

\( \left(1-\frac{\alpha^{2}}{2!}+\frac{\alpha^{4}}{4!}+\ldots\right)+i\left(\alpha-\frac{\alpha^{3}}{3!}+\ldots\right)=\cos\alpha+i\sin\alpha \)

זה “מוכיח” את נוסחת אוילר ומסיים את הסיפור כאן מבחינתנו.

ועכשיו וידוי קטן לסיום: גדי של התיכון תיעב טריגונומטריה (את זה כבר סיפרתי) ובאופן כללי לא אהב מתמטיקה במיוחד, אבל אי שם באמצע כיתה י”ב, אחרי אחד השיעורים, המורה שלו לפיזיקה הראה לנו את העניין הזה של טורי טיילור ונוסחת אוילר שהראיתי כאן. נראה לי שזו הייתה הפעם הראשונה שראיתי מתמטיקה שחורגת מחומר הלימוד של בית הספר ועם זאת עדיין קרובה אליו מספיק כדי שאוכל “להרגיש” אותה בידיים (כלומר לשבת, לעשות את החישובים בעצמי, לראות שזה יוצא ולהתמוגג). תחושת הפליאה הזו הייתה גם מה שהכווין אותי ללמוד מתמטיקה בהמשך (במקביל ללימודי מדעי המחשב שאליהם הגעתי בזכות הספר “אלגוריתמיקה” של דוד הראל). אני מקווה שהצלחתי להעביר חלק מתחושת הפליאה הזו לאלו ששרדו עד כאן.

נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: