על עקומות ואינטגרלים

מבוא

הפוסט הזה נולד מהרצון שלי לכתוב פוסט על אינטגרל מרוכב, שהוא נושא יפהפה ומרתק שנפתח כמובן עם הגדרה. ההגדרה בסיסית ומוכרת ואף אחד בעולם לא חולק עליה ולכן כמובן שהייתי צריך לשכנע את עצמי שהיא מוצדקת, מה שהוביל אותי למחילת ארנב: האינטגרל המרוכב הוא סוג של אינטגרל קווי, ולכן חזרתי אל הפוסט שלי על אינטגרל קווי כדי לראות מה כתבתי אז, כשהעמקתי לעובי הקורה. מה חשכו עיני כשגיליתי שבחלקים מסוימים חיפפתי ובחלקים אחרים פשוט טעיתי. אז הפוסט הזה כאן כדי לתקן (אל תחפשו לי טעויות בפוסט ההוא; פשוט הורדתי אותן וקישרתי לפוסט הזה במקום זאת למי שרוצים להעמיק).

מה אני הולך לעשות בפוסט הזה? מטרת העל שלי היא להסביר אינטגרלים קוויים (יש שני סוגים, אינטגרל קווי מסוג ראשון ואינטגרל קווי מסוג שני ולמרות שהם דומים עדיין יש מספיק מה לדבר על כל אחד בנפרד). בשביל זה אני ארצה קודם כל להזכיר מה זה בכלל אינטגרל, ולא פחות חשוב - נצטרך להסביר מה זה בכלל “קו” - או ליתר דיוק, מה זו עקומה. הלב הטכני של הפוסט הזה מתחבא לדעתי בכלל בנוסחה שנותנת לנו אורך של עקומה באמצעות אינטגרל, כלומר נגיע אל הלב הטכני עוד לפני שנציג אינטגרלים קוויים. בנוסף, אני מתכנן להיות פדנט אפילו יותר מהרגיל - למרות שהבלוג נקרא “לא מדויק” זה מהפוסטים הללו שבהם אני מרגיש שאני פשוט חייב להיות מדויק עד הסוף אחרת אני ארגיש שאני בכלל לא מבין את הנושא (על מי אני עובד? אני באמת לא מבין את הנושא כרגע! אני אולי אבין אותו רק אחרי שאסיים לכתוב את הפוסט הזה, ולא משנה כמה ספרים כבר קראתי על הנושא).

אז בואו נתחיל מההתחלה.

אינטגרל רימן

ראשית, מה זה בכלל אינטגרל? בהינתן פונקציה \( f \) ותחום מסוים שהיא מוגדרת בו, אפשר לחשוב על אינטגרל בתור סכום משוקלל של הערכים של הפונקציה בכל התחום. אם הפונקציה קבועה, האינטגרל שלה על התחום צריך להיות שווה לאורך/שטח/נפח שלו (המידה שלו, אם קופצים למושג מתמטי שלא אשתמש בו כאן). האופן שבו עושים את זה הוא על ידי קירובים שהולכים ומשתפרים, כפי שתמיד עושים באינפי.

האינטגרל הבסיסי ביותר הוא אינטגרל רימן ויש שתי שיטות סטנדרטיות להגדיר אותו שנותנות בסופו של דבר את אותו הדבר. שיטה מקובלת אחת משתמשת במשהו שנקרא סכומי דארבו וזו דרך די יפה ואלגנטית ואני לא אשתמש בה כאן. השניה, סכומי רימן, תתאים הרבה יותר למה שאני רוצה לעשות. באינטגרל רימן יש לנו פונקציה \( f:\left[a,b\right]\to\mathbb{R} \) ואנחנו רוצים להגדיר את הביטוי \( \int_{a}^{b}f\left(t\right)dt \). הרעיון הוא להגדיר אותו בעזרת קירובים: במקום לחשב סכום אינסופי, אנחנו מחלקים את הקטע \( \left[a,b\right] \) למספר סופי של קטעים, בוחרים נקודה שרירותית בכל אחד מהקטעים, וסוכמים את הערך של \( f \) על נקודה כזו באורך הקטע שבו הנקודה נמצאת. התקווה היא שככל שהקטעים הופכים לקטנים יותר ויותר, כך הסכום שנקבל יתקרב יותר ויותר אל משהו ספציפי; \( \int_{a}^{b}f\left(t\right)dt \) יוגדר להיות המשהו הספציפי הזה.

אם כן, בואו נגדיר חלוקה של \( \left[a,b\right] \). נסמן חלוקה כזו באות \( P \) (מלשון Partition) והיא כוללת סדרה של נקודות \( a=t_{0}<t_{1}<t_{2}<\ldots<t_{n}=b \) שאנחנו חושבים עליהן כמגדירות סדרה של \( n \) קטעים: \( \left[t_{0},t_{1}\right],\left[t_{1},t_{2}\right],\ldots,\left[t_{n-1},t_{n}\right] \). האיחוד של כל הקטעים הללו נותן את הקטע \( \left[a,b\right] \) המקורי. בשביל לפרמל את “הקטעים הופכים לקטנים יותר ויותר” אני מסמן \( \Delta t_{i}=t_{i}-t_{i-1} \) ומגדיר לכל חלוקה \( P \) את פרמטר החלוקה \( \lambda\left(P\right)=\max\left\{ \Delta t_{i}\right\} _{i=1}^{n} \), האורך של הקטע הארוך ביותר בחלוקה.

עכשיו כשיש לנו חלוקה אפשר לבחור באופן שרירותי נקודות מכל קטע שלה, וליצור את מה שקראתי לו סכום רימן: אז בוחרים סדרה \( t_{1}^{*},\ldots,t_{n}^{*} \) של נקודות כך ש-\( t_{i}^{*}\in\left[t_{i-1},t_{i}\right] \) ואז בונים את הסכום \( S_{P}=\sum_{i=1}^{n}f\left(t_{i}^{*}\right)\Delta t_{i} \) של הערכים של \( f \) בנקודות שבחרתי בתוך כל קטע, כפול אורך הקטע הזה. שימו לב שב-\( S_{P} \) מופיעה החלוקה \( P \) אבל לא טרחתי לציין במפורש את סדרת ה-\( t_{i}^{*} \)-ים שבחרתי; אינטואיטיבית זה בגלל שעבור כל בחירות נקודות בתוך החלוקה \( P \) אמור להתקיים אותו דבר נחמד.

מה הדבר הנחמד? הנה ההגדרה הפורמלית לאינטגרל שנעזרת בסכומי רימן: אם קיים מספר ממשי \( I\in\mathbb{R} \) כך שלכל \( \varepsilon>0 \) קיים \( \delta>0 \) כך שעבור כל חלוקה \( P \) שמקיימת \( \lambda\left(P\right)<\delta \) וכל סכום רימן \( S_{P} \) שמתאים לחלוקה הזו, מתקיים \( \left|S_{P}-I\right|<\varepsilon \), אז אומרים ש-\( \int_{a}^{b}f\left(t\right)dt \) מוגדר ו-\( \int_{a}^{b}f\left(t\right)dt=I \).

זו הייתה הגדרה טיפה ארוכה ומפותלת, אבל אין כאן שום דבר מורכב במיוחד למי שכבר התרגלו להגדרות \( \varepsilon-\delta \) בחדו”א, אז אני לא אתעכב עליה יותר מזה.

עקומות והאורך שלהן

הרעיון באינטגרלים קוויים הוא לבצע אינטגרציה שבה התחום הוא עקומה שחיה ב-\( \mathbb{R}^{n} \). מה זו עקומה? אינטואיטיבית זו קבוצת נקודות ב-\( \mathbb{R}^{n} \) שנראית כמו קו חד ממדי, אבל כזה שיכול להסתובב ולהתפתל - תחשבו על חוט מתוח שאנחנו נותנים לחתול להתפרע איתו. כמובן, אנחנו לא רוצים להתפרע יותר מדי - אסור לקו הזה להיקרע, או לבצע סיבובים חדים מדי; הדרך שלנו לפרמל את זה היא להגדיר עקומה בתור פונקציה \( \gamma:\left[a,b\right]\to\mathbb{R}^{n} \) שהיא גזירה ברציפות, מה שנקרא חלקה. אפשר לדמיין את מה ש-\( \gamma \) עושה בתור לקחת את הקטע \( \left[a,b\right] \), לשתול אותו במרחב \( \mathbb{R}^{n} \) ולעקם ולפתל אותו כמו חתול, בלי לקרוע - האובייקט שמתקבל הוא עדיין חד ממדי. אפשר לדמיין את מה ש-\( \gamma \) עושה גם בתור “טיול על העקומה”: יש לנו משתנה \( a\le t\le b \) שמתאר את הזמן הנוכחי של הטיול, שמתחיל בזמן \( a \) ומסתיים בזמן \( b \), ו-\( \gamma\left(t\right) \) אומר איפה בתוך \( \mathbb{R}^{n} \) אנחנו נמצאים בדיוק בזמן \( t \) של הטיול.

שימו לב ש-\( \gamma \) לא בדיוק מתארת קבוצת נקודות במישור - היא מתארת טיול על הקבוצה הזו. אפשר לסמן את הקבוצה הזו בסימון קונקרטי - \( C=\gamma\left(\left[a,b\right]\right) \) ואני לרוב קורא ל-\( C \) עקום. כלומר - העקום הוא אוסף הנקודות עצמו, העקומה היא דרך אפשרית אחת לתאר אותו (לפעמים גם משתמשים בביטוי פרמטריזציה של העקום כדי לתאר את \( \gamma \)). אפשר להוכיח שלא משנה איזו \( \gamma \) נבחר עבור \( C \) - כל עוד בחרנו \( \gamma \) “נחמדה מספיק”, תמיד נקבל את אותו ערך של אינטגרל - אבל אני לא אכנס לזה כאן.

לפני שאני מתחיל להשתמש בעקומות כדי לתאר אינטגרלים, יש שתי שאלות שאני רוצה לענות עליהן:

1. איך מגדירים את האורך של עקומה?
2. איך מחשבים את האורך של עקומה?

עבור 1 אפשר לתת הגדרה פשוטה למדי שלא מניחה כמעט כלום על \( \gamma \) מלבד זה שהיא רציפה. בשביל חישוב האורך נצטרך ש-\( \gamma \) תהיה גם חלקה, אבל בואו קודם נתחיל מהגדרת האורך של העקומה. שימו לב שההגדרה הזו לא תחול על כל העקומות, פשוט כי על פיה יוצא שיש עקומות בעלות אורך אינסופי למרות שהן נוצרות מהקטע \( \left[a,b\right] \) בעל האורך הסופי; אלו עקומות “פתולוגיות” חריגות, ואני לא אתעסק איתן; אני כן אגיד שאומרים שעקומה היא Rectifiable (לא יודע איך זה נקרא בעברית) אם ההגדרה שאתן עכשיו עובדת ונותנת אורך סופי.

הרעיון הבסיסי מאחורי ההגדרה הוא ההנחה/אקסיומה/וואטאבר שהמרחק הקצר ביותר בין שתי נקודות הוא הקו הישר שמחבר אותן - זה מה שקורה בגאומטריה האוקלידית, אבל לאו דווקא נכון בגאומטריות אחרות (תלוי מה זה “קו ישר”). אם מקבלים את ההנחה הזו, אז אפשר לחשוב על שיטת קירוב לאורך של עקומה שמתבססת על לקחת סדרת נקודות על העקומה, לחבר אותן בקווים ישרים ולקבל קירוב פוליגוני של העקומה על ידי משהו שקל לנו יחסית לחשב את האורך שלו כי לחשב אורך של קו זה קל. פורמלית, אם העקומה שלנו היא \( \gamma:\left[a,b\right]\to\mathbb{R}^{n} \), אז לוקחים חלוקה \( a=t_{0}<t_{1}<t_{2}<\ldots<t_{m}=b \) שאני מסמן ב-\( P \) כמו קודם, ועכשיו אפשר לסמן את הקירוב הפוליגוני ש-\( P \) מגדירה עם \( \pi\left(P\right) \) ולהגדיר את האורך שלו בתור

\( \left|\pi\left(P\right)\right|=\sum_{i=1}^{m}\|\gamma\left(t_{i}\right)-\gamma\left(t_{i-1}\right)\| \)

צריך טיפה להסביר מה קורה כאן. ראשית, אם \( v=\left(v_{1},\ldots,v_{n}\right)\in\mathbb{R}^{n} \) אז במטריקה האוקלידית מגדירים את הנורמה שלו להיות

\( \|v\|=\sqrt{\sum_{k=1}^{n}\left|v_{k}\right|^{2}} \)

זה קצת מפחיד אבל אם מסתכלים על המקרה של \( n=2 \) רואים שהמרחק בין שתי נקודות \( \left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right) \) יוצא

\( \|\left(x_{1},y_{1}\right)-\left(x_{1},y_{1}\right)\|=\sqrt{\left|x_{1}-x_{2}\right|^{2}+\left|y_{1}-y_{2}\right|^{2}} \)

וזה פשוט שימוש רגיל במשפט פיתגורס, אז הנורמה ה-\( n \)-ממדית היא פשוט הכללה של זה. מה שאולי טיפה פחות ברור הוא ש-\( \gamma\left(t_{i}\right)-\gamma\left(t_{i-1}\right) \) הוא הנקודה שהקו שמחבר אותה עם ראשית הצירים הוא מאותו אורך כמו הקו שמחבר את \( \gamma\left(t_{i-1}\right) \) עם \( \gamma\left(t_{i}\right) \) - זה שימוש בכלל המקבילית שקל להבין עם איור.

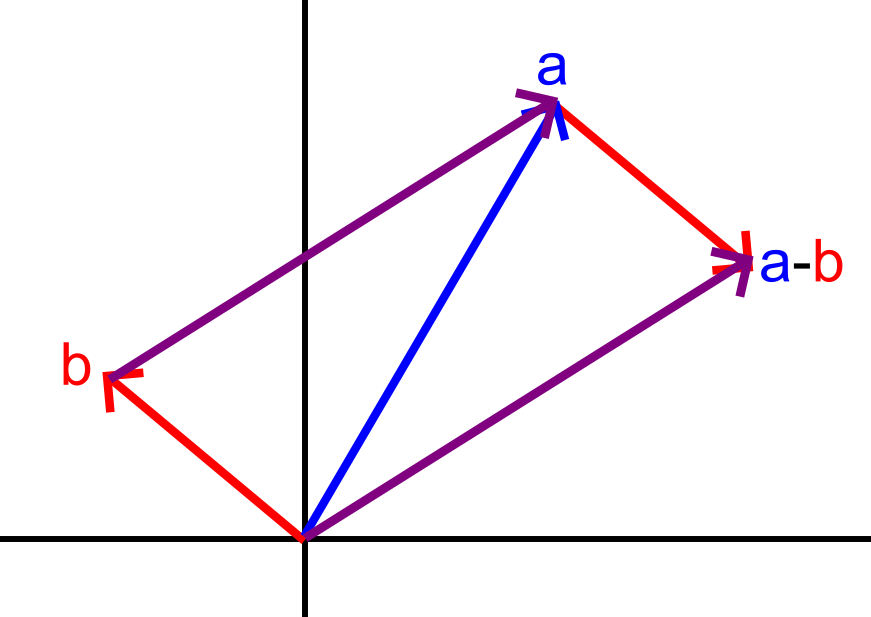
באיור הזה אני מצייר שתי נקודות \( a,b \), כשהוקטור אל \( a \) הוא כחול והוקטור אל \( b \) הוא אדום. הרעיון בכלל המקבילית הוא שכאשר אני מחבר שני וקטורים, אני מדביק עותק של כל אחד מהם לקצה של השני, כך שאני יוצאר מקבילית, והנקודה שבה שני העותקים הללו נפגשים היא הסכום. אצלנו אני מתעניין ב-\( a-b \) ולכן אני מצייר מקבילית שהוקטורים שבונים אותה הם \( b \) ו-\( a-b \) (שהוקטור שמתאים לו הוא סגול), ואפשר לראות איך אורך הוקטור של \( a-b \) (הקו הסגול התחתון יותר, שמחבר את \( a-b \) עם ראשית הצירים) זהה באורכו לקו הסגול העליון, שהוא מה שמחבר את \( b \) עם \( a \).

עכשיות אמרתי שהרעיון בקירוב פוליגוני הוא שהקו הישר בין שתי נקודות הוא תמיד קצר יותר מאשר העקומה שעוברת דרכן (ליתר דיוק - לא ארוך יותר, כי אולי גם העקומה היא קו ישר בין שתי הנקודות הללו) לכן אנחנו מצפים מאורך העקומה להיות חסם עליון עבור כל אורך של קירוב פוליגונלי אליה. מצד שני, ככל שאנחנו מוסיפים יותר ויותר נקודות כך אפשר לקוות שהקירובים שלנו מתקרבים יותר ויותר אל העקומה - כלומר, אנחנו מצפים לכך שהאורך של הקירובים ילך ויתקרב אל אורך העקומה עצמו, בלי “להיתקע” מתחת לאורך קטן יותר בדרך. לכן אנחנו מצפים שאורך העקומה יהיה החסם העליון הקטן ביותר של קבוצת אורכי הקירובים הפוליגונליים - או כמו שזה נקרא במתמטיקה, סופרמום. לכן אנחנו מגדירים את האורך של העקומה \( \gamma \) בין הנקודות \( a,b \) להיות \( \Lambda_{\gamma}\left(a,b\right)=\sup_{P}\left\{ \left|\pi\left(P\right)\right|\right\} \) כאשר \( P \) רץ על כל החלוקות הסופיות של \( \left[a,b\right] \). בשביל שההגדרה הזו באמת תעבוד, הכרחי שבכלל יהיה חסם סופי לקבוצה הזו, כלומר שיהיה קיים \( M \) כלשהו כך ש-\( \left|\pi\left(P\right)\right|\le M \) לכל חלוקה \( P \); אם אין כזה, העקום הוא Nonrectifiable.

זה מטפל בהגדרה, אבל מה עם חישוב של האורך? בשביל זה אני מכניס לתמונה את ההנחה ש-\( \gamma \) גזירה ברציפות, ואני רוצה להראות שבמקרה הזה יתקיים \( \Lambda_{\gamma}\left(a,b\right)=\int_{a}^{b}\|\gamma^{\prime}\left(t\right)\|dt \), אבל זה לא יהיה טריוויאלי להראות את זה - למעשה, זה הלב הטכני של הפוסט הזה.

ראשית, אינטואיציות: אם \( \gamma\left(t\right) \) היא פונקציה שמתארת טיול על העקומה, במובן של “בזמן \( t \) הייתי כאן וכאן”, אז הנגזרת שלה, \( \gamma^{\prime}\left(t\right) \), מתארת את מהירות הטיול הזה - מהירות במובן שנקרא בפיזיקה Velocity, כלומר כזה שמדבר גם על כיוון התנועה ולא רק על הגודל שלה. אם נסתכל על \( \|\gamma^{\prime}\left(t\right)\| \) נקבל את המהירות במובן של Speed, גודל בלבד שלא תלוי בכיוון. לכן האינטגרל \( \int_{a}^{b}\|\gamma^{\prime}\left(t\right)\|dt \) מודד “כמה מרחק עברתי”. זו נראית הגדרה כל כך מתבקשת שרוב הספרים מתחילים איתה וזהו; רק אני (ולמשל הספר של Tom Apostol שהחלק הזה של הפוסט מסתמך מאוד על דרך ההצגה שלו) מתעקש לדבר על הסופרמום (טוב, אם להודות על האמת, לא מעט ספרים מדברים על הסופרמום ואז אומרים בנפנוף ידיים שזה שווה לאינטגרל וגם זה בסדר).

שנית, למה זה בעצם טריקי? אני אראה עכשיו הוכחה שגויה, שהיא פחות או יותר משהו שהופיע בפוסט המקורי שלי. אנחנו לוקחים קירוב פוליגונלי עם \( P \) כלשהי:

\( \left|\pi\left(P\right)\right|=\sum_{i=1}^{m}\|\gamma\left(t_{i}\right)-\gamma\left(t_{i-1}\right)\| \)

ואז אנחנו אומרים - היי, אנחנו מכירים דרך טובה להתמודד עם ביטויים שהם הפרש של הפונקציה בשתי נקודות שונות; זה מזכיר לנו משפט אולטרה-שימושי מחדו”א, משפט הערך הממוצע של לגראנז'. המשפט הזה אומר שאם \( f:\left[a,b\right]\to\mathbb{R} \) היא פונקציה רציפה ובנוסף היא גזירה ב-\( \left(a,b\right) \) אז קיימת נקודה \( c\in\left(a,b\right) \) כך ש-\( f^{\prime}\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a} \) - הנגזרת של \( f \) מקבלת ב-\( c \) את הערך הממוצע של הפונקציה \( f \) בקטע. זה מאפשר לנו לומר ש-\( f\left(b\right)-f\left(a\right)=\left(b-a\right)f^{\prime}\left(c\right) \), כלומר להמיר את ההפרש בין ערכי הפונקציה בקטע, אל אורך הקטע כפול הנגזרת בתוכו. אז אם אני מפעיל את זה על הביטוי שלמעלה אני מקבל

\( \sum_{i=1}^{m}\|\gamma\left(t_{i}\right)-\gamma\left(t_{i-1}\right)\|=\sum_{i=1}^{m}\|\gamma^{\prime}\left(t_{i}^{*}\right)\|\Delta t_{i} \)

והדבר הזה נראה כמו סכום רימן של הפונקציה \( f\left(t\right)=\|\gamma^{\prime}\left(t\right)\| \), כלומר ככל שהחלוקה \( P \) קטנה יותר כך הקירוב הפוליגונלי שואף גם ל-\( \Lambda_{\gamma}\left(a,b\right) \) וגם אל \( \int_{a}^{b}\|\gamma^{\prime}\left(t\right)\|dt \). זה נראה מצוין, אבל הבעיה היא שאי אפשר להשתמש כאן במשפט הערך הממוצע של לגראנז’. כי המשפט הזה עובד עבור פונקציות שהטווח שלהן הוא \( \mathbb{R} \), ואילו במקרה שלנו \( \gamma \) היא פונקציה וקטורית, פונקציה שהטווח שלה הוא \( \mathbb{R}^{n} \), ובאופן כללי משפט הערך הממוצע לא עובד עבורן. לכן או שצריך עוד עבודה טכנית כדי להציל את ההוכחה הזו, או שצריך ללכת על הוכחה שונה, וזה מה שאני הולך לעשות כאן.

לפני שנעבור להוכחה, בואו נדבר שניה על מה זה בעצם אומר ש-\( \gamma \) היא פונקציה וקטורית, כי עד עכשיו החבאתי את המורכבות של זה בכוונה. בפועל זה אומר שקיימות פונקציות ממשיות \( \gamma_{1},\gamma_{2},\ldots,\gamma_{n}:\left[a,b\right]\to\mathbb{R} \) כך ש-\( \gamma\left(t\right)=\left(\gamma_{1}\left(t\right),\ldots,\gamma_{n}\left(t\right)\right) \). אפשר להוכיח שהרציפות של \( \gamma \) עוברת לפונקציות הרכיבים הללו, וש-\( \gamma^{\prime}\left(t\right)=\left(\gamma_{1}^{\prime}\left(t\right),\ldots,\gamma_{n}^{\prime}\left(t\right)\right) \) ובהמשך אני גם אשתמש בסימון \( \int_{a}^{b}\gamma\left(t\right)dt \) כשהכוונה היא לוקטור \( \left(\int_{a}^{b}\gamma_{1}\left(t\right)dt,\ldots,\int_{a}^{b}\gamma_{n}\left(t\right)dt\right) \).

עכשיו בואו נעבור להוכחה. הטריק מאחוריה די מזכיר את האופן שבו מגדירים אינטגרל לא מסוים ומחברים אותו אל האינטגרל המסוים עם המשפט היסודי של החדו”א. אנחנו נגדיר פונקציה ממשית \( s:\left[a,b\right]\to\mathbb{R} \) שמודדת את המרחק שעברנו לאורך העקום מתחילתו ועד הנקודה שהגענו אליה, כלומר \( s\left(t\right)=\Lambda_{\gamma}\left(a,t\right) \) (בפרט, \( s\left(a\right)=0 \)). אם נצליח להראות ש-\( s^{\prime}\left(t\right)=\|\gamma^{\prime}\left(t\right)\| \) בכל נקודה \( t\in\left[a,b\right] \), אז נוכל להשתמש במשפט היסודי של החדו”א כדי להראות ש-

\( \Lambda_{\gamma}\left(a,b\right)=s\left(b\right)-s\left(a\right)=\int_{a}^{b}s^{\prime}\left(t\right)dt=\int_{a}^{b}\|\gamma^{\prime}\left(t\right)\|dt \)

אז המטרה שלנו היא להוכיח שמתקיים \( s^{\prime}\left(t\right)=\|\gamma^{\prime}\left(t\right)\| \). זה יהיה קצת טריקי, ואני אצטרך שתי תוצאות לפני כן:

1. \( \Lambda_{\gamma}\left(a,b\right)\le\int_{a}^{b}\|\gamma^{\prime}\left(t\right)\|dt \), כלומר האינטגרל הוא קירוב מלמעלה של האורך.
2. פונקציית אורך העקומה היא חיבורית ("אדיטיבית") במובן הבא: אם \( c\in\left[a,b\right] \) אז \( \Lambda_{\gamma}\left(a,b\right)=\Lambda_{\gamma}\left(a,c\right)+\Lambda_{\gamma}\left(c,b\right) \)

נתחיל מ-1. בגלל ש-\( \Lambda_{\gamma}\left(a,b\right) \) הוגדר בתור סופרמום על קבוצה, אם נוכיח שכל איבר בקבוצה קטן או שווה למשהו, גם הסופרמום יהיה קטן או שווה ממנו. לכן אנחנו לוקחים חלוקה \( P \) כללית ורוצים להוכיח ש-\( \left|\pi\left(P\right)\right|\le\int_{a}^{b}\|\gamma^{\prime}\left(t\right)\|dt \). כאן נלך על פי ההגדרות ועל פי תכונות בסיסיות של אינטגרלים:

\( \left|\pi\left(P\right)\right|=\sum_{i=1}^{m}\|\gamma\left(t_{i}\right)-\gamma\left(t_{i-1}\right)\|=\sum_{i=1}^{m}\|\int_{t_{i-1}}^{t_{i}}\gamma^{\prime}\left(t\right)dt\|\le \)

\( \sum_{i=1}^{m}\int_{t_{i-1}}^{t_{i}}\|\gamma^{\prime}\left(t\right)\|dt=\int_{a}^{b}\|\gamma^{\prime}\left(t\right)\|dt \)

בואו נבין את המעברים. הראשון הוא פשוט הגדרת האורך שכבר ראינו. השני הוא שימוש במשפט היסודי של החדו”א. המעבר האחרון משתמש באדיטיביות של אינטגרלים (\( \int_{a}^{c}f\left(t\right)dt+\int_{c}^{b}f\left(t\right)dt=\int_{a}^{b}f\left(t\right)dt \) - דומה למה שאנחנו הולכים להוכיח עבור \( \Lambda \)). המעבר שבו מתחבא הלב הטכני הוא זה שמסתמך על \( \|\int_{t_{i-1}}^{t_{i}}\gamma^{\prime}\left(t\right)dt\|\le\int_{t_{i-1}}^{t_{i}}\|\gamma^{\prime}\left(t\right)\|dt \). כאן אני מרשה לעצמי סוף סוף לעצור ולא להוכיח את הטענה הזו, פשוט כי היא הכללה טבעית של טענה מוכרת עבור פונקציות ממשיות עם משתנה יחיד (להבדיל ממשפט הערך הממוצע של לגראנז’ שפשוט לא היה אפשר להכליל). אם רוצים את ההוכחה, היא נמצאת למשל בספר של Apostol ואולי יום אחד יהיה לי התקף של רצון עז להוכיח גם אותה - אבל הפעם אני נמנע מזה כי זה יאריך את הפוסט הארוך ממילא הזה אפילו עוד יותר.

עכשיו בואו נוכיח את האדיטיביות של \( \Lambda_{\gamma}\left(a,b\right) \). זה יהיה טיעון קליל וחמוד ומאוד חדו”אי באופי שלו. אנחנו לוקחים נקודה כלשהי \( c\in\left[a,b\right] \) ורוצים להוכיח ש–\( \Lambda_{\gamma}\left(a,b\right)=\Lambda_{\gamma}\left(a,c\right)+\Lambda_{\gamma}\left(c,b\right) \), אז יהיה מעורב פה אי שוויון דו כיווני. מכיוון ש-\( \Lambda_{\gamma} \) מוגדר בתור סופרמום על קבוצת איברים, הדרך להתמודד איתו היא על ידי לקיחת איבר כלשהו מהקבוצה ומעבר לרמה הזו של הדיון.

שימו לב שלפני שנוכיח \( \Lambda_{\gamma}\left(a,b\right)=\Lambda_{\gamma}\left(a,c\right)+\Lambda_{\gamma}\left(c,b\right) \) בכלל צריך להוכיח ש-\( \Lambda_{\gamma}\left(a,c\right),\Lambda_{\gamma}\left(c,b\right) \) מוגדרים בכלל - שתת-העקומות הללו הן Rectifiable, מה שלא נתון לי כי הנתון מדבר רק על \( \Lambda_{\gamma}\left(a,b\right) \). ובכן, בואו ניקח שתי חלוקות, חלוקה \( P_{1} \) של \( \left[a,b\right] \) וחלוקה \( P_{2} \) של \( \left[c,b\right] \). האיחוד של שתי החלוקות הללו נותן לי חלוקה \( P \) של \( \left[a,b\right] \) ואם אני מסתכל על הקירוב הפוליגונלי \( \pi\left(P\right) \) הוא כולל בדיוק את הקווים שב-\( \pi\left(P_{1}\right) \) ו-\( \pi\left(P_{2}\right) \) ולכן

\( \left|\pi\left(P_{1}\right)\right|+\left|\pi\left(P_{2}\right)\right|=\left|\pi\left(P\right)\right|\le\Lambda_{\gamma}\left(a,b\right) \)

בפרט, קיבלתי שקיים חסם מלעיל עבור \( \left|\pi\left(P_{1}\right)\right| \) וגם עבור \( \left|\pi\left(P_{2}\right)\right| \) ולכן \( \Lambda_{\gamma}\left(a,c\right),\Lambda_{\gamma}\left(c,b\right) \) קיימים. אבל כדי להראות את הכיוון הראשון של אי שוויון שאנחנו רוצים, \( \Lambda_{\gamma}\left(a,c\right)+\Lambda_{\gamma}\left(c,b\right)\le\Lambda_{\gamma}\left(a,b\right) \), נצטרך לעבוד עוד טיפה. ניקח את אי השוויון שקיבלנו

\( \left|\pi\left(P_{1}\right)\right|+\left|\pi\left(P_{2}\right)\right|\le\Lambda_{\gamma}\left(a,b\right) \)

נעביר אגף ונקבל

\( \left|\pi\left(P_{1}\right)\right|\le\Lambda_{\gamma}\left(a,b\right)-\left|\pi\left(P_{2}\right)\right| \)

אם אני משאיר את \( P_{2} \) קבוע ומרשה ל-\( P_{1} \) לרוץ על כל קבוצת החלוקות של \( \left[a,b\right] \) אנחנו רואים ש-\( \Lambda_{\gamma}\left(a,b\right)-\left|\pi\left(P_{2}\right)\right| \) הוא חסם מלעיל של אורכי כל החלוקות בקבוצה הזו, ולכן הסופרמום של הקבוצה גם כן קטן ממנו. הסופרמום הוא בדיוק \( \Lambda_{\gamma}\left(a,c\right) \) אז קיבלנו

\( \Lambda_{\gamma}\left(a,c\right)\le\Lambda_{\gamma}\left(a,b\right)-\left|\pi\left(P_{2}\right)\right| \)

אי השוויון הזה נכון לכל חלוקה \( P_{2} \) שניקח, ולכן אפשר להסיק ממנו ש-\( \Lambda_{\gamma}\left(a,c\right)\le\Lambda_{\gamma}\left(a,b\right)-\Lambda_{\gamma}\left(b,c\right) \). אם זה נראה לכם ברור, נהדר! אבל למקרה שלא, בואו נראה את זה פורמלית בכל זאת. אני אשתמש בטכניקה הסטנדרטית: אני אראה שלכל \( \varepsilon>0 \) מתקיים \( \Lambda_{\gamma}\left(a,c\right)\le\Lambda_{\gamma}\left(a,b\right)-\Lambda_{\gamma}\left(b,c\right)+\varepsilon \) ומכיוון שזה קורה לכל \( \varepsilon>0 \) אז אי השוויון חייב להתקיים גם כשאני מציב \( \varepsilon=0 \), כי באופן כללי - אם \( X\le Y+\varepsilon \) לכל \( \varepsilon>0 \) אבל \( X>Y \) אז ניקח \( \varepsilon=\frac{X-Y}{2} \) ונקבל

\( X\le Y+\varepsilon=Y+\frac{X-Y}{2}=\frac{X+Y}{2}<\frac{X+X}{2}=X \)

וקיבלנו \( X<X \), וזו בוודאי סתירה. אז חזרה למקרה שלנו, לקחנו \( \varepsilon>0 \) כלשהו, ועכשיו אנחנו מסתכלים על \( \Lambda_{\gamma}\left(b,c\right) \). מכיוון שזה סופרמום של קבוצה, אז קיים בקבוצה איבר \( \left|\pi\left(P_{2}\right)\right| \) כך ש-\( \left|\pi\left(P_{2}\right)\right|\ge\Lambda_{\gamma}\left(b,c\right)-\varepsilon \), כלומר \( -\left|\pi\left(P_{2}\right)\right|\le-\Lambda_{\gamma}\left(b,c\right)+\varepsilon \) ולכן

\( \Lambda_{\gamma}\left(a,c\right)\le\Lambda_{\gamma}\left(a,b\right)-\left|\pi\left(P_{2}\right)\right|\le\Lambda_{\gamma}\left(a,b\right)-\Lambda_{\gamma}\left(b,c\right)+\varepsilon \)

כמו שרצינו. זה מראה ש-\( \Lambda_{\gamma}\left(a,c\right)\le\Lambda_{\gamma}\left(a,b\right)-\Lambda_{\gamma}\left(b,c\right) \), ואחרי העברת אגפים \( \Lambda_{\gamma}\left(a,c\right)+\Lambda_{\gamma}\left(b,c\right)\le\Lambda_{\gamma}\left(a,b\right) \) וזה הכיוון הראשון של אי השוויון שרצינו.

עבור הכיוון השני אז בואו ניקח חלוקה \( P \) של \( \left[a,b\right] \). ונראה שלא משנה מה, \( \left|\pi\left(P\right)\right|\le\Lambda_{\gamma}\left(a,c\right)+\Lambda_{\gamma}\left(c,b\right) \) ומזה ינבע ש-\( \Lambda_{\gamma}\left(a,b\right)\le\Lambda_{\gamma}\left(a,c\right)+\Lambda_{\gamma}\left(c,b\right) \).

אם אני לוקח את \( P \) ומוסיף לה את הנקודה \( c \) (אלא אם \( c \) כבר נמצאת בה), מה משתנה? אני יכול עכשיו להסתכל על \( P \) בתור איחוד של שתי חלוקות, חלוקה \( P_{1} \) של \( \left[a,c\right] \) וחלוקה \( P_{2} \) של \( \left[c,b\right] \). החלוקות הללו כוללת בדיוק את אותם קטעים כמו ב-\( P \) למעט אולי קטע \( \left[t_{i-1},t_{i}\right] \) שעבורו \( c\in\left(t_{i-1},t_{i}\right) \), ובמקרה זה הקטע הזה הוחלף בשני הקטעים \( \left[t_{i-1},c\right] \) ו-\( \left[c,t_{i}\right] \). כעת נכניס לתמונה את אי שוויון המשולש ב-\( \mathbb{R}^{n} \):

\( \|\gamma\left(t_{i}\right)-\gamma\left(t_{i-1}\right)\|=\|\gamma\left(t_{i}\right)-\gamma\left(c\right)+\gamma\left(c\right)-\gamma\left(t_{i-1}\right)\|\le\|\gamma\left(t_{i}\right)-\gamma\left(c\right)\|+\|\gamma\left(c\right)-\gamma\left(t_{i-1}\right)\| \)

כלומר, אורך הקטע שהסרנו קטן או שווה לאורך שני הקטעים שהוספנו, ולכן נקבל

\( \left|\pi\left(P\right)\right|\le\left|\pi\left(P_{1}\right)\right|+\left|\pi\left(P_{2}\right)\right|\le\Lambda_{\gamma}\left(a,c\right)+\Lambda_{\gamma}\left(c,b\right) \)

מה שמסיים את הכיוון הזה, ואת הוכחת האדיטיביות. עכשיו אפשר לחזור אל העיקר: ההוכחה ש-\( \Lambda_{\gamma}\left(a,b\right)=\int_{a}^{b}\|\gamma^{\prime}\left(t\right)\|dt \) שכבר צמצמנו אל הצורך להוכיח רק \( s^{\prime}\left(t\right)=\|\gamma^{\prime}\left(t\right)\| \) כאשר, כזכור, \( s\left(t\right)=\Lambda_{\gamma}\left(a,t\right) \). בשביל לראות איך עושים את זה, בואו נחזור ליסודות - איך מגדירים נגזרת? \( s^{\prime}\left(t\right)=\lim_{h\to0}\frac{s\left(t+h\right)-s\left(t\right)}{h} \). אני אנסה לחסום את הביטוי הזה משני הכיוונים על ידי גבולות ששואפים לאותו דבר כש-\( h\to0 \) ואז להשתמש בכלל הסנדוויץ'.

בתור התחלה, בואו נסתכל על \( \|\gamma^{\prime}\left(t\right)\| \). אם אני מנסה להבין אותו בתור גבול, אני מקבל

\( \lim_{h\to0}\|\frac{\gamma\left(t+h\right)-\gamma\left(t\right)}{h}\|=\lim_{h\to0}\frac{1}{h}\|\gamma\left(t+h\right)-\gamma\left(t\right)\| \)

כאן \( \|\gamma\left(t+h\right)-\gamma\left(t\right)\| \) הוא בעצם האורך של קו ישר שמחבר את שתי הנקודות \( \gamma\left(t+h\right) \) ו-\( \gamma\left(t\right) \). כלומר, זה ביטוי שחסום מלמעלה על ידי אורך העקומה \( \Lambda_{\gamma}\left(t,t+h\right) \) (אם \( h<0 \) אז \( t+h \) בעצם באה קודם ולכן צריך לכתוב \( \Lambda_{\gamma}\left(t+h,t\right) \) אבל העיקרון זהה). אבל

\( \Lambda_{\gamma}\left(t,t+h\right)=\Lambda_{\gamma}\left(a,t+h\right)-\Lambda_{\gamma}\left(a,t\right)=s\left(t+h\right)-s\left(t\right) \)

בזכות האדיטיביות שהוכחנו קודם, כך שאנחנו מקבלים

\( \|\gamma\left(t+h\right)-\gamma\left(t\right)\|\le s\left(t+h\right)-s\left(h\right) \)

ולכן

\( \frac{1}{h}\|\gamma\left(t+h\right)-\gamma\left(t\right)\|\le\frac{s\left(t+h\right)-s\left(t\right)}{h} \)

אגף שמאל פה שואף ל-\( \|\gamma^{\prime}\left(t\right)\| \) כאשר \( h\to0 \), אז נשאר רק לחסום מלמעלה את \( \frac{s\left(t+h\right)-s\left(t\right)}{h} \). בשביל זה אני אסתמך על כך שכבר הוכחתי \( \Lambda_{\gamma}\left(a,b\right)\le\int_{a}^{b}\|\gamma^{\prime}\left(t\right)\|dt \), כלומר

\( s\left(t+h\right)-s\left(t\right)=\Lambda_{\gamma}\left(t,t+h\right)\le\int_{t}^{t+h}\|\gamma^{\prime}\left(t\right)\|dt \)

עכשיו, שימו לב שאם אני מגדיר פונקציה \( f:\left[a,b\right]\to\mathbb{R} \) על ידי \( f\left(x\right)=\int_{a}^{x}\|\gamma^{\prime}\left(t\right)\|dt \) אז בזכות העובדה ש-\( \|\gamma^{\prime}\left(t\right)\| \) היא פונקציה רציפה (מה שנובע מכך ש-\( \gamma \) חלקה) המשפט היסודי של החדו”א נותן לי ש-\( f^{\prime}=\|\gamma^{\prime}\left(t\right)\| \) בכל \( \left[a,b\right] \) וש-\( \int_{t}^{t+h}\|\gamma^{\prime}\left(t\right)\|dt=f\left(t+h\right)-f\left(t\right) \). כלומר, קיבלתי את החסם

\( s\left(t+h\right)-s\left(t\right)\le f\left(t+h\right)-f\left(t\right) \)

וכשנחלק את שניהם ב-\( h \) נקבל

\( \frac{s\left(t+h\right)-s\left(t\right)}{h}\le\frac{f\left(t+h\right)-f\left(t\right)}{h} \)

וכאשר \( h\to0 \) אז אגף ימין שואף, על פי הגדרה, אל \( f^{\prime}\left(t\right)=\|\gamma^{\prime}\left(t\right)\| \), וזה בדיוק מה שרצינו. זה מסיים את ההוכחה: הראינו שאורך העקומה \( \gamma \) הוא בדיוק \( \int_{a}^{b}\|\gamma^{\prime}\left(t\right)\|dt \), במקרה שבו \( \gamma \) חלקה, מה שמצדיק את ההגדרה של אורך העקומה באמצעות האינטגרל הזה כדי לחסוך את כל ההתעסקות הטכנית שראינו כאן.

אינטגרל קווי (מסוג ראשון)

אפשר לחשוב על אינטגרל רימן בתור סכימה של הערכים של \( f \) לאורך הקו הישר שמחבר את \( a \) אל \( b \) ביקום החד-ממדי \( \mathbb{R} \). הרעיון באינטגרל קווי הוא להכליל את אותו קונספט של סכימה בדיוק אל ופונקציות שחיים בתוך מרחב גדול יותר - למשל, ב-\( \mathbb{R}^{n} \), אבל כדי לשמור על החד-ממדיות של אינטגרל רימן, אנחנו לא סוכמים את הערכים של \( f \) בכל המרחב, אלא על תת-מרחב ש”נראה כמו” משהו חד ממדי, או במילים אחרות - על עקומה. הסיבה שיש לנו שני סוגים של אינטגרלים קוויים היא שיש שני סוגים של פונקציות שאנחנו רוצים לבצע עליהן אינטגרציה: פונקציה סקלרית \( f:\mathbb{R}^{n}\to\mathbb{R} \) שמחזירה מספר ממשי בודד, ופונקציה וקטורית \( F:\mathbb{R}^{n}\to\mathbb{R}^{n} \) שמחזירה וקטור מהמרחב שעליו הפונקציה פועלת (אני לא מכיר דרך נפוצה שבה מטפלים בפונקציות שבהן הטווח הוא \( \mathbb{R}^{m} \) כך ש-\( m\ne n,1 \)).

שתי ההנחות הקבועות שלי בהמשך יהיו שהפונקציה \( f \) או \( F \) שאני מבצע לה אינטגרציה היא רציפה, ושהעקומה שאני מבצע עליה את האינטגרציה מיוצגת על ידי \( \gamma \) שהיא פונקציה חלקה (גזירה ובעלת נגזרת רציפה). בלי אלו ההוכחות שלי לא הולכות לעבוד (ואני לא בטוח אם הן יכולות לעבוד בכלל או שאפשר לתת דוגמאות נגדיות פתולוגיות).

בואו נתחיל מלדבר על המקרה הראשון. אני אסמן ב-\( \int_{C}fd\gamma \) אינטגרל של \( f \) על העקום \( C \). בפוסט הקודם שלי על אינטגרלים קוויים דיברתי קצת על מה שנדרש מ-\( \gamma \) כדי שהאינטגרל על \( C \) לא יהיה תלוי בפרמטריזציה \( \gamma \) המדויקת, אבל הפעם אני לא אכנס לזה כי זה לא קשור למה שאני רוצה להוכיח. מה אני כן רוצה להוכיח? את השוויון \( \int_{C}fd\gamma=\int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt \) שבו בדרך כלל משתמשים כדי להגדיר את משמעות הביטוי \( \int_{C}fd\gamma \). זה אומר שאני צריך להתחיל מלהגדיר את \( \int_{C}fd\gamma \) בדרך אחרת, בתור הכללה טבעית של סכומי רימן.

בואו נתחיל שוב מאינטואיציה. מה בעצם קורה בביטוי \( \int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt \)? אם אנחנו לוקחים את הפונקציה הקבועה \( f\left(x\right)=1 \), אנחנו מקבלים בדיוק את האינטגרל שחישב את האורך של \( \gamma \). אפשר לדמיין את \( \gamma \) כאילו היא מתארת חוט של חומר שמפוזר במרחב, ואת \( f \) כאילו היא מתארת את צפיפות החומר בכל נקודה במרחב, ואנחנו רוצים לחשב את כמות החומר הכוללת; אם הצפיפות היא 1 בכל נקודה, הכמות הזו תהיה בדיוק אורך החוט, אבל אנחנו רוצים לטפל בסיטואציה היותר מורכבת של צפיפות משתנה. אפשר גם לחשוב על זה בצורה הרגילה שבה חושבים על אינטגרלים: באינטגרל רגיל, \( \int_{a}^{b}f\left(t\right)dt \), אנחנו לכאורה לוקחים את הערך \( f\left(t\right) \) של הפונקציה בנקודה קונקרטית \( t \), כופלים באורך של “המרחק מ-\( t \) אל הנקודה הבאה אחריה”, אורך שאנחנו מסמנים ב-\( dt \) וחושבים עליו בתור מספר קטן יותר מכל מספר ממשי, וסוכמים את הכל. אז גם ב-\( \int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt \) אפשר לחשוב שאנחנו לוקחים את הערך של \( f \) בנקודה קונקרטית - הפעם בנקודה הקונקרטית על העקומה \( \gamma\left(t\right) \) שהיא בעצמה הנקודה שמגיעים אליה בטיול על העקומה שמגיע לנקודה הקונקרטית \( t \), ואז כופלים את ערך הפונקציה הזו ב”מרחק מ-\( \gamma\left(t\right) \) אל הנקודה הבאה על \( \gamma \) אחריה”. ראינו כבר שמרחק כזה הוא \( \|\gamma^{\prime}\left(t\right)\|dt \), אבל כל זה היה נפנופי ידיים אינטואיטיביים בלבד; אין כאן משהו פורמלי. לפורמליזם נגיע עכשיו.

את התשתית כבר יש לנו - אנחנו מבינים את הרעיון של לקחת חלוקה \( P \) של \( \left[a,b\right] \) שמורכבת מהנקודות \( a=t_{0}<t_{1}<t_{2}<\ldots<t_{m}=b \) (אני משתמש ב-\( m \) לאינדקס האחרון כי \( n \) תפוס על ידי המימד של המרחב) ולהסתכל על החלוקה שהיא משרה על העקומה \( \gamma \). עכשיו נמשיך בדיוק כמו עם סכומי רימן הרגילים: בוחרים סדרה \( t_{1}^{*},\ldots,t_{m}^{*} \) של נקודות כך ש-\( t_{i}^{*}\in\left[t_{i-1},t_{i}\right] \) ואז בונים את הסכום \( S_{P}^{\gamma}=\sum_{i=1}^{m}f\left(\gamma\left(t_{i}^{*}\right)\right)\Delta\gamma_{i} \) כאשר \( f\left(\gamma\left(t_{i}^{*}\right)\right) \) הוא באופן מובן מאליו הערך של \( f \) על הנקודה בעקומה שמגיעים אליה בזמן \( t_{i}^{*} \), ו-\( \Delta\gamma_{i} \) הוא המרחק בין \( \gamma\left(t_{i}\right) \) ו-\( \gamma\left(t_{i-1}\right) \).

הגענו להגדרה של האינטגרל עצמו: אם קיים מספר \( I \) כך שלכל \( \varepsilon>0 \) קיים \( \delta>0 \) כך שלכל חלוקה \( P \) עם \( \lambda\left(P\right)<\delta \) מתקיים \( \left|S_{P}^{\gamma}-I\right|<\varepsilon \), אז אומרים ש-\( \int_{C}fd\gamma \) קיים ו-\( \int_{C}fd\gamma=I \). זה ממש 1:1 ההגדרה של אינטגרל רימן הרגיל. נשאר רק לקבל עבורה נוסחה.

בואו נסתכל על המרחק \( \Delta\gamma_{i} \) שמופיע בסכום שבנינו. עבדנו ממש קשה כדי לקבל נוסחה שימושית למרחק הזה אז בואו נשתמש בה עכשיו: \( \Delta\gamma_{i}=\int_{t_{i-1}}^{t_{i}}\|\gamma^{\prime}\left(t\right)\|dt \). במבט ראשון הייצוג הזה ל-\( \Delta\gamma_{i} \) נראה לי מעורר חלחלה. בגרסאות המקוריות והכושלות של הפוסט הזה כתבתי \( \Delta\gamma_{i}=\left|\gamma\left(t_{i}\right)-\gamma\left(t_{i-1}\right)\right| \) ואז השתמשתי בלגראז’ כדי לקבל \( \Delta\gamma_{i}=\Delta t_{i}\cdot\left|\gamma^{\prime}\left(c_{i}\right)\right| \) וקיבלתי מייד משהו שנראה כמו סכום רימן של \( \int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt \). אלא שכאמור, השימוש הזה בלגראנז’ הוא פשוט שגוי. אני לא יכול לעשות אותו, כי \( \gamma \) היא לא פונקציה ממשית אלא פונקציה וקטורית.

העניין הוא שקיימת הכללה של משפט לגראנז’ שבה אני כן יכול להשתמש - הכללה עבור אינטגרלים. הנה הניסוח המדויק: אם \( g:\left[a,b\right]\to\mathbb{R} \) היא פונקציה רציפה, אז קיימת \( c\in\left(a,b\right) \) כך ש-\( \int_{a}^{b}g\left(t\right)dt=g\left(c\right)\left(b-a\right) \). במקרה שלנו, \( g\left(t\right)=\|\gamma^{\prime}\left(t\right)\| \). זו פונקציה ממשית, כי הנורמה של וקטור היא מספר ממשי בודד. זו פונקציה רציפה כי היא הרכבה של פונקציה רציפה (הנורמה) על פונקציה שהנחתי שהיא רציפה (הנחתי ש-\( \gamma \) חלקה, לכן \( \gamma^{\prime} \) רציפה). לכן אפשר להשתמש במשפט הזה עבור \( \Delta\gamma_{i}=\int_{t_{i-1}}^{t_{i}}\|\gamma^{\prime}\left(t\right)\|dt \) ולקבל שקיים \( t_{i}^{*}\in\left(t_{i-1},t_{i}\right) \) כך ש-\( \Delta\gamma_{i}=\|\gamma^{\prime}\left(t_{i}^{*}\right)\|\Delta t_{i} \), כמו שרציתי.

אינטואיטיבית, סיימנו: אנחנו אומרים “היי, תראו, מצאנו ייצוג ל-\( S_{P}^{\gamma} \) שנראה בדיוק כמו סכום רימן רגיל!” כשהייצוג הזה הוא \( S_{P}^{\gamma}=\sum_{i=1}^{m}f\left(\gamma\left(t_{i}^{*}\right)\right)\|\gamma^{\prime}\left(t_{i}^{*}\right)\|\Delta t_{i} \), אבל אם רוצים להיות ממש פורמליים צריך להיזהר. למשל, בביטוי של הסכום מופיע \( t_{i}^{*} \) פעמיים - פעם אחת בתוך \( \gamma^{\prime}\left(t_{i}^{*}\right) \), ולשם הוא הגיע בעזרת משפט לגראנז’ האינטגרלי שהמציא אותו יש מאין, אבל הוא גם מופיע בתוך \( f\left(\gamma\left(t_{i}^{*}\right)\right) \) ולשם הוא הגיע סתם כי בחרנו סדרת נקודות שרירותית לחלוטין, הרבה לפני שבכלל דיברנו על משפט לגראנז’ האינטגרלי. בניסוח זהיר צריך להפוך את היוצרות - קודם לקבל את סדרת הנקודות שלגראנז’ נותן, ואז לומר “מכיוון שבסכום רימן אנחנו בוחרים נקודות באופן שרירותי אז ניקח את הנקודות שמצאנו קודם”. בואו נעשה את זה מסודר טיפ טופ עד הסוף, כי זה הפוסט שבו אני מרכז את כל הקטנוניות שלי.

אני רוצה להוכיח \( \int_{C}fd\gamma=\int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt \). הדרך החדו”אית הפורמלית להוכיח ששני דברים הם שווים היא להוכיח שלכל \( \varepsilon>0 \) מתקיים

\( \left|\int_{C}fd\gamma-\int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt\right|<\varepsilon \)

טריק חדו”אי ידוע בשביל להוכיח דבר כזה הוא למצוא מספר \( S \) שקרוב לשני הביטויים הללו עד כדי \( \frac{\varepsilon}{2} \):

\( \left|\int_{C}fd\gamma-S\right|<\frac{\varepsilon}{2} \)

\( \left|S-\int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt\right|<\frac{\varepsilon}{2} \)

אם נמצא מספר כזה, נוכל ללכת לביטוי המקורי, לחבר ולחסר בו את \( S \) ולהשתמש באי שוויון המשולש:

\( \left|\int_{C}fd\gamma-\int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt\right|=\left|\left(\int_{C}fd\gamma-S\right)+\left(S-\int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt\right)\right|\le \)

\( \left|\int_{C}fd\gamma-S\right|+\left|S-\int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt\right|\le\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon \)

מי ה-\( S \) הזה יהיה? כמובן, הוא יהיה סכום רימן שקרוב מספיק לשני הביטויים הללו. בואו נבנה אותו בזהירות כדי שסדרת ה-\( t_{i}^{*} \)-ים תתקבל בצורה נכונה.

ראשית, אנחנו יודעים שעבור \( \frac{\varepsilon}{2} \) קיים \( \delta_{1}>0 \) כך שלכל חלוקה \( P \) עם \( \lambda\left(P\right)<\delta_{1} \), לכל סכום רימן \( S_{P}^{\gamma} \) שנבנה על החלוקה \( P \) עם בחירה של סדרת נקודות כלשהי, מתקיים \( \left|\int_{C}fd\gamma-S_{P}^{\gamma}\right|<\frac{\varepsilon}{2} \). אני עדיין לא מגדיר את \( S \) המדובר; בינתיים רק קיבלתי את \( \delta_{1} \).

בנוסף, שעבור \( \frac{\varepsilon}{2} \) קיים \( \delta_{2}>0 \) כך שלכל חלוקה \( P \) עם \( \lambda\left(P\right)<\delta_{2} \), לכל סכום רימן \( S_{P} \) שנבנה על החלוקה \( P \) עם בחירה של סדרת נקודות כלשהי, מתקיים \( \left|S_{P}-\int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt\right|<\frac{\varepsilon}{2} \). גם פה: עוד לא בניתי את \( S \), רק מצאתי את \( \delta_{2} \).

עכשיו אני אגדיר \( \delta=\min\left\{ \delta_{1},\delta_{2}\right\} \). ואקח חלוקה כלשהי \( P \) של \( \left[a,b\right] \) כך ש-\( \lambda\left(P\right)<\delta \) (זו יכולה להיות חלוקה אחידה, למשל; זה לא ממש משנה לי). שימו לב שגם בשלב הזה עדיין לא בניתי את \( S \); אבל אני כבר יודע שכל סכום רימן שייבנה על פי \( P \) הולך להיות קרוב לאינטגרלים שלעיל. העניין הוא שאני צריך למצוא \( S \) ספציפי כך ש-\( S=S_{P}=S_{P}^{\gamma} \) למרות ש-\( S_{P} \) ו-\( S_{P}^{\gamma} \) מוגדרים בצורה שונה - זה בדיוק האופן שבו לגראנז’ נכנס לעניין.

אם כן, אני מפעיל את לגראנז’ על החלוקה \( P \) ומוצא סדרת נקודות \( t_{1}^{*},t_{2}^{*},\ldots,t_{m}^{*} \) כך ש-\( \Delta\gamma_{i}=\|\gamma^{\prime}\left(t_{i}^{*}\right)\|\Delta t_{i} \), ועכשיו אני מגדיר:

\( S=\sum_{i=1}^{m}f\left(\gamma\left(t_{i}^{*}\right)\right)\|\gamma^{\prime}\left(t_{i}^{*}\right)\|\Delta t_{i} \)

עכשיו שיחקתי אותה, כי מצד אחד אם אני אסתכל על סכום הרימן שנוצר על ידי הפונקציה \( f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\| \), החלוקה \( P \) וסדרת הנקודות \( t_{1}^{*},t_{2}^{*},\ldots,t_{m}^{*} \), הסכום הזה הוא בדיוק

\( S_{P}=\sum_{i=1}^{m}f\left(\gamma\left(t_{i}^{*}\right)\right)\|\gamma^{\prime}\left(t_{i}^{*}\right)\|\Delta t_{i}=S \)

ומצד שני אם אני אסתכל על סכום הרימן \( S_{P}^{\gamma} \) שנוצר על ידי העקומה \( \gamma \), החלוקה \( P \), סדרת הנקודות \( t_{1}^{*},t_{2}^{*},\ldots,t_{m}^{*} \) והפונקציה \( f \), הסכום הזה הוא בדיוק

\( S_{P}^{\gamma}=\sum_{i=1}^{m}f\left(\gamma\left(t_{i}^{*}\right)\right)\Delta\gamma_{i}=\sum_{i=1}^{m}f\left(\gamma\left(t_{i}^{*}\right)\right)\|\gamma^{\prime}\left(t_{i}^{*}\right)\|\Delta t_{i}=S \)

וקיבלתי את \( S \) המבוקש שלי, מה שמסיים את ההוכחה: ראינו ש-\( \int_{C}fd\gamma=\int_{a}^{b}f\left(\gamma\left(t\right)\right)\|\gamma^{\prime}\left(t\right)\|dt \). מבחינתי הסיפור של הוכחת הנוסחה הזו סגור ואני עכשיו בסדר עם ספרים שמשתמשים בה פשוט בתור ההגדרה.

אינטגרל קווי (מסוג שני)

אינטגרל קווי מסוג שני מטפל בסיטואציה שבה מבצעים אינטגרל על פונקציה וקטורית, \( F:\mathbb{R}^{n}\to\mathbb{R}^{n} \). היה אפשר לחשוב על כל מני דרכים לעשות את זה: אפשר למשל להתייחס אל \( F \) בתור \( F\left(x\right)=\left(f_{1}\left(x\right),\ldots,f_{n}\left(x\right)\right) \) כשכל \( f_{i} \) היא פונקציה סקלרית ובמקרה הזה כבר טיפלנו עם אינטגרל קווי מסוג ראשון. בצורה הזו היינו מקבלים אינטגרל שהתוצאה שלו היא וקטור. אני לא רואה משהו שמונע מאיתנו להגדיר דבר כזה, כמו שאני לא רואה סיבה לא להגדיר כפל מטריצות “איבר-איבר”. זו פשוט לא הגדרה שימושית במיוחד.

מה כן הגדרה שימושית? או, אם אמרנו שימושים אז כאן אין מנוס מלהיכנס לפיזיקה כי אינטגרל קווי מסוג שני משמש שם לתיאור אחד מהדברים הבסיסיים ביותר במכניקה - תיאור של עבודה.

בואו נחשוב על הסיטואציה הבאה - אנחנו לוקחים כדורגל ומעיפים אותו גבוה לאוויר, בקו אנכי לגמרי. מה שיקרה הוא שהכדורגל יתחיל לעוף במהירות מסוימת, וככל שכח הכובד יפעל עליו כך המהירות תקטן עוד ועוד עד אשר הכדורגל ייעצר לרגע באוויר, ואז יתחיל לצבור מהירות לכיוון ההפוך. עד שיפול בחזרה למטה. בכל הזמן הזה פעל על הכדור כוח אחד ויחיד - כוח הכובד. בהתחלה הוא הקטין את מהירות הכדור, ואחר כך הוא הגדיל אותה. מה השתנה? דרך אחת לחשוב על כך היא זו: בהתחלה הכדור זז למעלה בזמן שכוח הכובד פעל למטה, ואחר כך הכדור זז למטה תוך כדי שכוח הכובד פועל למטה. יש כאן קשר בין וקטור הכוח (כלומר לא רק הגודל שלו, גם הכיוון שלו) ומסלול התנועה של הכדור.

הנה עוד סיטואציה לדוגמא: נדמיין לווין שמסתובב סביב כדור הארץ במסלול מעגלי לגמרי. מסלול מעגלי שכזה לא מתרחש “מעצמו”; החוק הראשון של ניוטון אומר שאם לא מופעלים על גוף כוחות, הוא יתמיד במסלול שהוא קו ישר. מסלול מעגלי נוצר רק כשבכל רגע משנים את כיוון התנועה של האובייקט. כאן ספציפית אפשר לדמיין שהלווין נע שמאלה בזמן שכדור הארץ מפעיל עליו כוח למטה, בניצב לכיוון התנועה של הלווין. זה גורם לכיוון התנועה של הלווין להשתנות ולהיות “שמאלה וקצת למטה” ; בשלב הזה הוא כבר זז קצת אבל כדור הארץ ממשיך להפעיל עליו כוח שניצב לכיוון התנועה שלו, וכן הלאה. בסיטואציה כזו של תנועה מעגלית מושלמת (ולא, נאמר, שהלווין נע במעין אליפסה) הגודל של המהירות של הלווין (מה שנקרא speed, להבדיל מ-velocity) הולך להישאר קבוע - זה שונה מהכדורגל שבו המהירות השתנתה כל הזמן. מה ההבדל? בסיפור של הלווין הכוח פועל בניצב לכיוון התנועה של הלווין, ובסיפור הכדורגל וקטור הכוח היה חופף לכיוון התנועה (או שהוא היה זהה לו, או שהוא היה הפוך בכיוונו).

בואו נעבור לפורמליזם הפיזיקלי. בפיזיקה משתמשים ב-\( v\left(t\right) \) כדי לתאר את וקטור המהירות של גוף בזמן \( t \). אם אנחנו במרחב תלת ממדי, למשל, אז \( v\left(t\right)=\left(v_{x}\left(t\right),v_{y}\left(t\right),v_{z}\left(t\right)\right) \). המהירות במובן של speed של הוקטור הזה היא \( \|v\|=\sqrt{v_{x}^{2}+v_{y}^{2}+v_{z}^{2}} \), אבל אפשר לפשט את הסימונים אם מכניסים לתמונה מכפלה סקלרית. באופן כללי, מכפלה סקלרית של שני וקטורים \( a,b\in\mathbb{R}^{n} \) היא \( a\cdot b=\sum_{i=1}^{n}a_{i}b_{i} \), ולא קשה לראות ש-\( \|v\|^{2}=v\cdot v \) (למי שזוכרים אלגברה לינארית, מכפלה סקלרית היא מקרה פרטי של מכפלה פנימית).

עכשיו, בפיזיקה יש לנו את החוק השני של ניוטון שמתאר את האופן שבו כוח שפועל על גוף משפיע על המהירות שלו: \( F=ma \), כאשר \( F \) הואה כוח שפועל על הגוף ו-\( a \) היא התאוצה של הגוף, כלומר \( a=v^{\prime} \) (הפיזיקאים מעדיפים סימון כמו \( a=\frac{dv}{dt} \) ועושים איתו להטוטים אבל אני בכוונה אמנע מכך כאן). עכשיו, מערכת שכוללת גוף וכוח שפועל עליו יכולה להיות מסובכת למדי: הכוח משפיע על התאוצה, שהיא הנגזרת הראשונה של המהירות, ולכן הנגזרת השנייה של המיקום, אבל המיקום עצמו עשוי להשפיע על הכוח כי באופן כללי הכוח תלוי במיקום האובייקט במרחב. אם נפתח את זה עד הסוף נקבל משוואה דיפרנצאלית וזה יכול להיות אתגר להתמודד עם דבר כזה, אז הפיזיקאים מוצאים דרכים להתמודד עם הקשיים בלי ללכת איתם ראש בראש, ואחת מהדרכים הללו היא לדבר על אנרגיה.

אנרגיה היא גודל מספרי כלשהו שניתן לחשב עבור מערכת, והרעיון בו הוא שהחישוב הוא כזה שהערך של האנרגיה נשאר קבוע גם כשהמערכת עוברת שינויים (הרעיון הזה של אינוריאנטה ככלי להבנה של מערכות מסובכות הוא להיט גם במתמטיקה; הפוסט הראשון בבלוג דיבר על זה). אחד מהגדלים שצריך לחשב כדי לקבל את האנרגיה של מערכת הוא האנרגיה הקינטית של העצמים שנמצאים בה, שמתארת גודל שנובע מהמהירות שלהם. עבור גוף בעל מסה \( m \) ומהירות \( v \), האנרגיה הקינטית היא \( \frac{m\|v\|^{2}}{2}=\frac{m\left(v\cdot v\right)}{2} \). עכשיו, לפני שאתקדם, הנה להטוט חמוד: אם \( a\left(t\right),b\left(t\right) \) הן שתי פונקציות וקטוריות, \( a,b:\mathbb{R}\to\mathbb{R}^{n} \), אז לא קשה להראות בעזרת חוקי הנגזרות הרגילים שמתקיים

\( \left(a\cdot b\right)^{\prime}=\left(\sum_{i=1}^{n}a_{i}b_{i}\right)^{\prime}=\sum_{i=1}^{n}a_{i}^{\prime}b_{i}+\sum_{i=1}^{n}a_{i}b_{i}^{\prime}=a^{\prime}\cdot b+a\cdot b^{\prime} \)

לכן, אם אני אסמן \( T=\frac{m\|v\|^{2}}{2} \) כדי לתאר את האנרגיה הקינטית של גוף, ואז אחשב את קצב השינוי שלה, אני אקבל

\( T^{\prime}=\frac{m}{2}\left(v\cdot v\right)^{\prime}=mv^{\prime}\cdot v=F\cdot v \)

כלומר, השינוי באנרגיה הקינטית של הגוף הוא הכוח \( F \) שפועל עליו, כפול וקטור המהירות של הגוף - זה תואם את הדיון שלמעלה, ומן הסתם לא במקרה - ההגדרה של אנרגיה קינטית מיועדת כדי שזה יעבוד. עכשיו, נפנוף הידיים הפיזיקאי אומר בשלב הזה ש-\( F\cdot v \) מתאר את השינוי הרגעי באנרגיה בהתאם לשינוי הרגעי בזמן, ולכן \( \int_{a}^{b}F\cdot vdt \) הולך לתאר את השינוי באנרגיה לאורך פרק הזמן \( a\le t\le b \), מה שנקרא העבודה של הכוח על הגוף. עכשיו, אם נתאר ב-\( \gamma \) את המסלול שהעצם עבר בפרק הזמן הזה, אז \( v=\gamma^{\prime} \) (כי מהירות היא תמיד הנגזרת של המקום), ולכן השינוי באנרגיה של הגוף יהיה \( \int_{a}^{b}F\cdot\gamma^{\prime}dt \). עכשיו אפשר להחזיר את מה שהסתרנו - הרי \( F \) היא פונקציה שתלויה לא בזמן אלא במקום של העצם בכל רגע נתון, כלומר ב-\( \gamma\left(t\right) \), אז את האינטגרל אפשר לכתוב בתור

\( \int_{a}^{b}F\left(\gamma\left(t\right)\right)\cdot\gamma^{\prime}dt \)

הדבר הזה הוא איך שמוגדר אינטגרל קווי מסוג שני. לפעמים הוא מסומן גם בתור \( \int_{C}F\cdot\gamma d\gamma \), בדומה למה שקורה לאינטגרל קווי מסוג ראשון, אבל צריך לזכור שכאן הכפל בין \( F \) ל-\( \gamma \) הוא מכפלה סקלרית וחישוב האינטגרל בפועל מסתמך עליה: \( \int_{C}F\cdot\gamma d\gamma=\int_{a}^{b}F\left(\gamma\left(t\right)\right)\cdot\gamma^{\prime}dt \).

ושוב עולה אצלי השאלה - האם אני חייב פשוט להגדיר את האינטגרל להיות \( \int_{a}^{b}F\left(\gamma\left(t\right)\right)\cdot\gamma^{\prime}dt \)? או שאני יכול להשתמש בגישת סכומי רימן גם כאן? בואו נחשוב איך סכום רימן כזה הולך להיראות כאן. כרגיל, אני אקח את הקטע \( \left[a,b\right] \) ואחלק אותו לחלוקה \( P \) כלשהי עם נקודות הביניים \( a=t_{0}\le t_{1}\le\ldots\le t_{m}=b \). אני אקח נקודה \( t_{i}^{*}\in\left[t_{i-1},t_{i}\right] \) מתוך כל קטע כזה, אחשב את הפונקציה באותה נקודה של העקום שמתאימה לזמן \( t_{i}^{*} \) כלומר אסתכל על \( F\left(\gamma\left(t_{i}^{*}\right)\right) \), ואת זה אני אכפול באורך… לא, רגע, עוד לא. כאמור, \( F\left(\gamma\left(t_{i}^{*}\right)\right) \) הוא וקטור שאנחנו לא רוצים לקחת את כולו; אנחנו רוצים לקחת רק את הגודל של ההיטל שלו על הכיוון שאליו העקום \( \gamma \) הולך בזמן \( t_{i}^{*} \). בשביל דברים כאלו יש לנו מכפלה סקלרית.

הנה עוד תזכורת על מכפלה סקלרית. מצד אחד, \( u\cdot v=\sum_{i=1}^{n}u_{i}v_{i} \) וזו דרך לחשוב על מכפלה סקלרית בתור איך בדיוק מחשבים אותה. מצד שני, אפשר להראות ש-\( u\cdot v=\|u\|\cdot\|v\|\cdot\cos\theta \) כש-\( \theta \) היא הזווית שבין שני הוקטורים. עכשיו, אפשר לחשוב על \( \|u\|\cdot\cos\theta \) בתור גודל ההיטל של \( u \) על הציר ש-\( v \) מגדיר - הנה דרך לדמיין את זה (החלק של \( v \) עד הקו המקווקו, שצבעתי בסגול, הוא מאורך \( \|u\|\cdot\cos\theta \)):

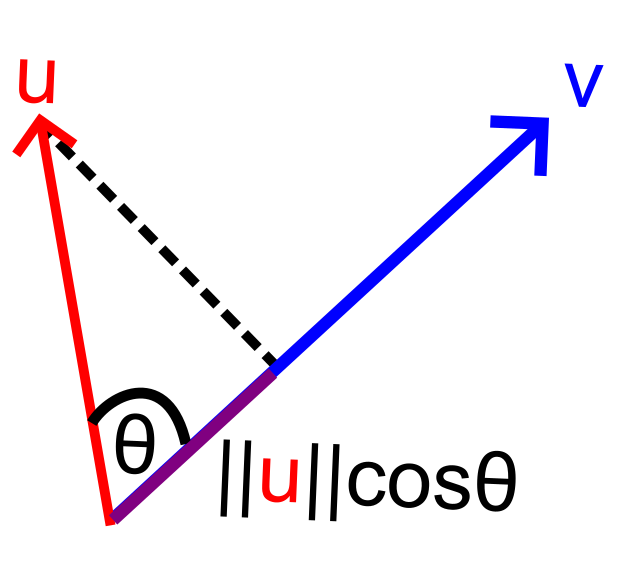
ולכן אפשר לחשוב על \( u\cdot v \) בתור גודל ההיטל של \( u \) על \( v \), כל זה כפול הגודל של \( v \). אם אנחנו רוצים להשתמש ב-\( v \) רק בתור וקטור שמצביע על כיוון, בלי לכפול בגודל שלו, אפשר פשוט לנרמל אותו - להסתכל על המכפלה \( u\cdot\frac{v}{\|v\|} \). אפשר לעשות את זה גם כאן: אם אנחנו רוצים רק את וקטור הכיוון שאליו \( \gamma \) הולכת בזמן \( t_{i}^{*} \) אפשר להסתכל על הוקטור \( \frac{\gamma^{\prime}\left(t_{i}^{*}\right)}{\|\gamma^{\prime}\left(t_{i}^{*}\right)\|} \). כמובן, זה מניח ש-\( \gamma^{\prime}\left(t_{i}^{*}\right)\ne0 \), כי אם \( \gamma^{\prime}\left(t_{i}^{*}\right)=0 \) אין מה לחלק בנורמה שלו אבל יותר גרוע מזה, הוא בכלל לא מגדיר כיוון מוגדר ולכן כל הדיון חסר תוחלת; אבל אנחנו מניחים שהפרמטריזציה היא “נחמדה” ולכן אין לה סיבה לבצע עצירות פתאומיות, אז נתעלם מזה באלגנטיות.

אם כן, הפונקציה שאנחנו רוצים שתופיע לנו בסכום הרימן, ותוכפל כרגיל ב-\( \Delta\gamma_{i} \) כמו שקרה באינטגרל קווי מסוג ראשון, היא הפונקציה \( \frac{F\left(\gamma\left(t_{i}^{*}\right)\right)\cdot\gamma^{\prime}\left(t_{i}^{*}\right)}{\|\gamma^{\prime}\left(t_{i}^{*}\right)\|} \), ולכן סכום הרימן שלי הולך להיות

\( S_{P}^{\gamma}=\sum_{i=1}^{m}\frac{F\left(\gamma\left(t_{i}^{*}\right)\right)\cdot\gamma^{\prime}\left(t_{i}^{*}\right)}{\|\gamma^{\prime}\left(t_{i}^{*}\right)\|}\cdot\Delta\gamma_{i} \)

ובכן, זו נראית כמו חתיכת מהומה ענקית! אבל בואו ניזכר שעשינו לא מעט עבודה כשדיברנו על אינטגרל קווי מסוג ראשון כדי להראות שאפשר לכתוב \( \Delta\gamma_{i}=\|\gamma^{\prime}\left(t_{i}^{*}\right)\|\Delta t_{i} \). זה לא נכון לכל סדרה שרירותית של נקודות \( t_{i}^{*} \)! אבל בהינתן חלוקה \( P \) תמיד אפשר למצוא סדרה ספציפית כזו של נקודות שעבורן השוויון יתקיים - זה היה שימוש במשפט לגראנז’ האינטגרלי. לכן, עבור בחירה מתאימה של נקודות כאלו, סכום הרימן שלנו הופך להיות

\( S_{P}^{\gamma}=\sum_{i=1}^{m}F\left(\gamma\left(t_{i}^{*}\right)\right)\cdot\gamma^{\prime}\left(t_{i}^{*}\right)\cdot\Delta t_{i} \)

ואפשר להשתמש בדיוק באותה הוכחה שראינו במקרה של אינטגרל קווי מסוג ראשון כדי להראות שבגלל שהסכום הזה הוא בעצם אותו דבר כמו סכום רימן של האינטגרל הרגיל \( \int_{a}^{b}F\left(\gamma\left(t\right)\right)\cdot\gamma^{\prime}dt \), אנחנו מקבלים \( \int_{C}F\cdot\gamma d\gamma=\int_{a}^{b}F\left(\gamma\left(t\right)\right)\cdot\gamma^{\prime}dt \). למעשה, אפשר ממש לחשוב על מה שעשינו פה בתור רדוקציה למקרה של אינטגרל קווי מסוג ראשון - כאילו אמרנו “היי, בואו נסתכל על הפונקציה \( \frac{F\left(\gamma\left(t\right)\right)\cdot\gamma^{\prime}\left(t\right)}{\|\gamma^{\prime}\left(t\right)\|} \), זו פונקציה סקלרית אז בואו נחשב לה אינטגרל קווי מסוג ראשון”. זה מסיים עבורי את הסיפור של אינטגרל קווי מסוג שני - גם פה, אני עכשיו בסדר גמור עם פשוט להגדיר אותו בתור \( \int_{a}^{b}F\left(\gamma\left(t\right)\right)\cdot\gamma^{\prime}dt \).

ומה עם אינטגרל מרוכב?

כל המהומה הזו נולדה מהנסיון לשכנע את עצמי שההגדרה של אינטגרל מרוכב היא “מה שהיא צריכה להיות” למרות שאין שום צורך בשכנוע כזה מלכתחילה כי מרגע שמתחילים עם ההגדרה הזו קורים קסמים. אז אני לא יכול לסיים את הפוסט הזה בלי לדבר גם על ההגדרה הזו.

ההגדרה עצמה דומה מאוד להגדרה של אינטגרל קווי מסוג שני: יש לנו עקומה \( C \), רק שהפעם היא לא עקומה ב-\( \mathbb{R}^{n} \) אלא במישור המרוכב, כלומר אני מתאר אותה עם פונקציה שאסמן \( z:\left[a,b\right]\to\mathbb{C} \). יש לנו פונקציה מרוכבת \( f:\mathbb{C}\to\mathbb{C} \), ואנחנו מגדירים

\( \int_{C}f\left(z\right)dz=\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt \)

זה מאוד, מאוד מזכיר אינטגרל קווי מסוג שני, אבל יש הבדל ברור אחד - הכפל שמופיע בתור האינטגרל הימני הוא לא מכפלה סקלרית, הוא פשוט פעולת הכפל הרגילה של מספרים מרוכבים, שהיא די שונה ממכפלה סקלרית. אם אני כותב את המספר המרוכב \( a+bi \) בתור \( \left(a,b\right) \), אז נקבל את המכפלה \( \left(a_{1},b_{1}\right)\cdot\left(a_{2},b_{2}\right)=\left(a_{1}a_{2}-b_{1}b_{2},a_{1}b_{2}+a_{2}b_{1}\right) \) שהיא כמובן גם לא סקלר ממשי אלא עדיין משהו עם שני רכיבים ממשיים שונים, וגם היא ערבוביה מוחלטת של המקדמים, בזכות פעולת הכפל המוזרה של מספרים מרוכבים. אז אי אפשר להגיד שזה פשוט לקחת את ההגדרה של אינטגרל קווי מסוג שני ולהשתמש בה על מרוכבים; ועוד דבר שהפריע לי מאוד הוא למה להשתמש דווקא באינטגרל קווי מסוג שני ולא באינטגרל קווי מסוג ראשון, שלכאורה מתאים יותר לסיטואציה של פונקציה שמחזירה סקלר שאפשר לכפול בו כפל רגיל. למה לא להגדיר \( \int_{C}f\left(z\right)dz=\int_{a}^{b}f\left(z\left(t\right)\right)\|z^{\prime}\left(t\right)\|dt \)?

ובכן, אפשר היה להגדיר ככה, זה פשוט לא היה שימושי כמו מה שכן הוגדר. הטעות הבסיסית שלי כשניגשתי לנושא הייתה לחשוב שאינטגרל מרוכב מוגדר בצורה דומה לאינטגרל קווי, כשבפועל הוא לא: הוא מוגדר בצורה דומה למה שנקרא אינטגרל רימן-סטילטיס.

מה הרעיון של אינטגרל רימן-סטילטיס? זה כמובן ראוי לפוסט משלו, אז אשאר כאן יחסית ממוקד. באינטגרל רימן, סכום רימן נראה כמו \( S_{P}=\sum_{i=1}^{n}f\left(t_{i}^{*}\right)\Delta t_{i} \) כאשר \( \Delta t_{i}=t_{i}-t_{i-1} \) והרעיון הוא ש-\( \Delta t_{i} \) מייצג אורך קטע. בעצם, אפשר לחשוב על הסכום הזה בתור סכום ממושקל, כשהערך של פונקציה בקטע מסוים מקבלת משקל שמתאים לאורך שלו. זה תואם את האינטואיציה שלנו כשאנו חושבים על אינטגרל בתור “השטח שמתחת לגרף הפונקציה \( f \)”. אבל למה להגביל את עצמנו? אפשר להשתמש בפונקציות משקל שונות ומשונות שנקראות אינטגרטורים. אם כן, לוקחים פונקציה \( g:\left[a,b\right]\to\mathbb{R} \) ומגדירים סכום רימן-סטילטיס בתור \( S_{P}=\sum_{i=1}^{n}f\left(t_{i}^{*}\right)\left(g\left(t_{i}\right)-g\left(t_{i-1}\right)\right) \). אם כל הדבר הזה מתכנס למשהו באותו מובן שבו סכום רימן התכנס, מסמנים את התוצאה ב-\( \int_{a}^{b}fdg \), כאשר כאן ה-\( dg \) במקום \( dt \) רומז לנו ש-\( g \) הוא אינטגרטור. אינטגרל רימן ה”רגיל” מתקבל אם בוחרים \( g\left(t\right)=t \).

במקרים שבהם \( g \) חלקה, אפשר להמיר את החישוב של אינטגרל רימן-סטילטיס בחישוב של אינטגרל רימן, באופן דומה למה שכבר ראינו אבל למרבה השמחה אפילו עוד יותר קל כי כאן אפשר להשתמש במשפט הערך הממוצע המקורי של לגראנז’, על \( g \) עצמה, ולקבל \( g\left(t_{i}\right)-g\left(t_{i-1}\right)=g^{\prime}\left(t_{i}^{*}\right)\Delta t_{i} \) לכל תת-קטע. מרגע שיש לנו את זה, זו פשוט חזרה על ההוכחה שכבר ראינו קודם ש-\( \int_{a}^{b}fdg=\int_{a}^{b}f\left(t\right)g^{\prime}\left(t\right)dt \) (שימו לב שכאן הפרמטר של \( f \) הוא פשוט \( t \); הוא לא \( g\left(t\right) \) כמו שקורה באינטגרל קווי).

אינטגרל מרוכב מוגדר בצורה דומה מאוד. יש לנו את העקומה \( \gamma:\left[a,b\right]\to\mathbb{C} \) שממלאת את התפקיד של \( g \), אבל במקום לסכום “סתם” ערכים של \( f \), אנחנו סוכמים ערכים של \( f\left(\gamma\left(t\right)\right) \), כלומר אנחנו מסתכלים על משהו דמוי רימן-סטילטיס עבור אינטגרטור \( \gamma \) והפונקציה \( f\circ\gamma \). מכיוון שאנחנו כבר ממש ממש ממש בסוף, בואו עוד פעם אחת אחרונה ודי נעשה את הכל פורמלי, כדי שלא יהיו לי יותר דאגות.

אם כן: נתונה לנו פונקציה \( f:\mathbb{C}\to\mathbb{C} \) ועקומה \( z:\left[a,b\right]\to\mathbb{C} \). אנחנו לוקחים חלוקה \( P \) של \( \left[a,b\right] \), ולכל בחירת נקודות \( t_{i}^{*} \) אנחנו בונים את הסכום \( S_{P}^{z}=\sum_{i=1}^{n}f\left(z\left(t_{i}^{*}\right)\right)\left(z\left(t_{i}\right)-z\left(t_{i-1}\right)\right) \). הפעם זה סכום של מספרים מרוכבים; גם \( f\left(z\left(t_{i}^{*}\right)\right) \) וגם \( \left(z\left(t_{i}\right)-z\left(t_{i-1}\right)\right) \) הם מספרים מרוכבים. הגדרת ההתכנסות נשארת זהה: אם קיים \( I\in\mathbb{C} \) כך שלכל \( \varepsilon>0 \) קיים \( \delta \) כך שלכל חלוקה \( P \) עם \( \lambda\left(P\right)<\delta \) וכל בחירת נקודות עבור חלוקה כזו, מתקיים \( \left|S_{P}^{z}-I\right|<\varepsilon \), אז אומרים ש-\( \int_{C}f\left(z\right)dz=I \). הפעם הערך המוחלט ב-\( \left|S_{P}^{z}-I\right| \) הוא פונקציית הערך המוחלט של מספרים מרוכבים: \( \left|a+bi\right|=\sqrt{a^{2}+b^{2}} \).

אני רוצה להוכיח שתחת ההגדרה הזו מתקיים השוויון \( \int_{C}f\left(z\right)dz=\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt \), אבל מה בעצם הולך באגף ימין? זה לא אינטגרל רימן רגיל. אמנם, המשתנה של הפונקציה שבאינטגרל הוא מספר ממשי, \( t\in\left[a,b\right] \), אבל הפונקציות עצמן הן עדיין מרוכבות ולא דיברתי על אינטגרלים של פונקציות מרוכבות עם משתנה ממשי. למרבה המזל, זה ממש פשוט: כל פונקציה מרוכבת \( g:\left[a,b\right]\to\mathbb{C} \) אפשר להציג בתור \( g\left(t\right)=x\left(t\right)+iy\left(t\right) \) כאשר \( x,y:\mathbb{R}\to\mathbb{R} \) הן פונקציות ממשיות, ואז אפשר להגדיר

\( \int_{a}^{b}g\left(t\right)dt=\int_{a}^{b}x\left(t\right)dt+i\int_{a}^{b}y\left(t\right)dt \)

כאשר כאן באגף ימין יש שני אינטגרלים רגילים של פונקציות ממשיות. זה גם מה שעשינו כשלקחנו אינטגרל של פונקציה וקטורית, כשהתעסקנו באינטגרלים קוויים. דבר דומה קורה גם עבור נגזרות:

\( g^{\prime}\left(t\right)=\lim_{h\to0}\frac{g\left(t+h\right)-g\left(t\right)}{h}=\lim_{h\to0}\left(\frac{x\left(t+h\right)-x\left(t\right)}{h}+i\frac{y\left(t+h\right)-y\left(t\right)}{h}\right)=x^{\prime}\left(t\right)+iy^{\prime}\left(t\right) \)

אז זה מה שנצטרך לעשות כדי להוכיח את השוויון \( \int_{C}f\left(z\right)dz=\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt \) - לפרק לשני חלקים שאחד ממשי והשני מדומה, ולהוציא את ה-\( i \) החוצה. אז בואו ונכתוב

\( f\left(z\left(t\right)\right)=u\left(t\right)+iv\left(t\right) \)

\( z\left(t\right)=x\left(t\right)+iy\left(t\right) \)

\( z^{\prime}\left(t\right)=x^{\prime}\left(t\right)+iy^{\prime}\left(t\right) \)

ועכשיו:

\( \int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt=\int_{a}^{b}\left[u\left(t\right)+iv\left(t\right)\right]\left[x^{\prime}\left(t\right)+iy^{\prime}\left(t\right)\right]dt \)

\( =\int_{a}^{b}\left[u\left(t\right)x^{\prime}\left(t\right)-v\left(t\right)y^{\prime}\left(t\right)\right]dt+i\int_{a}^{b}\left[u\left(t\right)y^{\prime}\left(t\right)+v\left(t\right)x^{\prime}\left(t\right)\right]dt \)

זה נראה כמו סמטוחה אחת גדולה, אבל אין עם זה בעיה - כל עוד גם \( \int_{C}f\left(z\right)dz \) מתכנן להיראות כמו סמטוחה אחת גדולה דומה כשנסיים איתו. בואו נכתוב סכום רימן כללי עבורו:

\( \sum_{i=1}^{n}f\left(z\left(t_{i}^{*}\right)\right)\left(z\left(t_{i}\right)-z\left(t_{i-1}\right)\right) \)

בינתיים אני לא יכול לפשט את \( z\left(t_{i}\right)-z\left(t_{i-1}\right) \) כי אין לי אנלוג ישיר למשפט לגראנז’ עבור פונקציות עם טווח מרוכב. אז מה אני אעשה? אני אלך עם הראש בקיר ואציב דברים:

\( \sum_{i=1}^{n}f\left(z\left(t_{i}^{*}\right)\right)\left(z\left(t_{i}\right)-z\left(t_{i-1}\right)\right)=\sum_{i=1}^{n}\left[\left(u\left(t_{i}^{*}\right)+iv\left(t_{i}^{*}\right)\right)\left(x\left(t_{i}\right)+iy\left(t_{i}\right)-x\left(t_{i-1}\right)-iy\left(t_{i-1}\right)\right)\right]= \)

\( =\sum_{i=1}^{n}\left[u\left(t_{i}^{*}\right)\left(x\left(t_{i}\right)-x\left(t_{i-1}\right)\right)-v\left(t_{i}^{*}\right)\left(y\left(t_{i}\right)-y\left(t_{i-1}\right)\right)\right]+ \)

\( +i\sum_{i=1}^{n}\left[u\left(t_{i}^{*}\right)\left(y\left(t_{i}\right)-y\left(t_{i-1}\right)\right)+v\left(t_{i}^{*}\right)\left(x\left(t_{i}\right)-x\left(t_{i-1}\right)\right)\right] \)

בינתיים זה נראה טוב, אבל שוד ושבר - יש לנו גם את הביטוי \( x\left(t_{i}\right)-x\left(t_{i-1}\right) \) וגם את הביטוי \( y\left(t_{i}\right)-y\left(t_{i-1}\right) \) ולא נוכל להשתמש בלגראנז’ סימולטנית על שניהם. לכן אני אנקוט בטקטיקה אחרת - אני אפצל את הכל עוד פעם ואקבל מהאינטגרל המקורי סכום של ארבעה אינטגרלים, ומסכום הרימן המקורי ארבעה סכומים. בואו נכתוב אותם זה לצד זה:

• \( \int_{a}^{b}u\left(t\right)x^{\prime}\left(t\right)dt \) אל מול \( \sum_{i=1}^{n}u\left(t_{i}^{*}\right)\left(x\left(t_{i}\right)-x\left(t_{i-1}\right)\right) \)
• \( -\int_{a}^{b}v\left(t\right)y^{\prime}\left(t\right)dt \) אל מול \( -\sum_{i=1}^{n}v\left(t_{i}^{*}\right)\left(y\left(t_{i}\right)-y\left(t_{i-1}\right)\right) \)
• \( i\int_{a}^{b}u\left(t\right)y^{\prime}\left(t\right)dt \) אל מול \( i\sum_{i=1}^{n}u\left(t_{i}^{*}\right)\left(y\left(t_{i}\right)-y\left(t_{i-1}\right)\right) \)
• \( i\int_{a}^{b}v\left(t\right)x^{\prime}\left(t\right)dt \) אל מול \( i\sum_{i=1}^{n}v\left(t_{i}^{*}\right)\left(x\left(t_{i}\right)-x\left(t_{i-1}\right)\right) \)

עכשיו אני אוכיח שמתקיים\( \int_{C}f\left(z\right)dz=\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt \) על פי ההגדרה של \( \int_{C}f\left(z\right)dz \). כלומר, ניקח \( \varepsilon>0 \) ונוכיח שקיימת \( \delta>0 \) כך שאם \( P \) היא חלוקה כלשהי עם \( \lambda\left(P\right)<\delta \), אז \( \left|S_{P}^{z}-\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt\right|<\varepsilon \).

עכשיו, ראינו איך אפשר לפצל גם את \( S_{P}^{z} \) וגם את \( \int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt \) לארבעה חלקים שמתאימים זה לזה בזוגות. לכן כדי לחסום את ההפרש, אני משתמש באי שוויון המשולש על פיצול לארבעה חלקים של כל אחד מהביטויים. בואו נראה איך דבר כזה נראה, סכמטית:

\( \left|\left(A_{1}+B_{1}+C_{1}+D_{1}\right)-\left(A_{2}+B_{2}+C_{2}+D_{2}\right)\right|\le\left|A_{1}-A_{2}\right|+\left|B_{1}-B_{2}\right|+\left|C_{1}-C_{2}\right|+\left|D_{1}-D_{2}\right| \)

במקרה שלנו המקבילה ל-\( \left|A_{1}-A_{2}\right| \) תהיה

\( \left|\int_{a}^{b}u\left(t\right)x^{\prime}\left(t\right)dt-\sum_{i=1}^{n}u\left(t_{i}^{*}\right)\left(x\left(t_{i}\right)-x\left(t_{i-1}\right)\right)\right| \)

ודי ברור מה יהיו שאר המקבילות (ושהכפל ב-\( -1 \) או ב-\( i \) לא משפיע; הערך המוחלט מעלים אותו).

עכשיו צריך לשים לב לנקודה עדינה: \( \int_{a}^{b}u\left(t\right)x^{\prime}\left(t\right)dt \) נראה כמו החישוב של אינטגרל רימן-סטילטיס, וכבר ראינו ש-\( \int_{a}^{b}u\left(t\right)x^{\prime}\left(t\right)dt=\int_{a}^{b}u\left(t\right)dx \). המשמעות של השוויון הזה היא שסכומי רימן-סטילטיס של \( \int_{a}^{b}u\left(t\right)dx \) מתקרבים אל \( \int_{a}^{b}u\left(t\right)x^{\prime}\left(t\right)dt \). כלומר, עבור \( \frac{\varepsilon}{4} \) קיים \( \delta_{1} \) כך שאם \( P \) חלוקה עם \( \lambda\left(P\right)<\delta_{1} \), אז כל סכום רימן-סטילטיס ובפרט הסכום \( \sum_{i=1}^{n}u\left(t_{i}^{*}\right)\left(x\left(t_{i}\right)-x\left(t_{i-1}\right)\right) \) יהיה קרוב אל \( \int_{a}^{b}u\left(t\right)x^{\prime}\left(t\right)dt \) עד כדי \( \frac{\varepsilon}{4} \).

באותו האופן אנחנו מוצאים \( \delta_{2},\delta_{3},\delta_{4} \) עבור שלושת הביטויים האחרים, ואז מגדירים \( \delta=\min\left\{ \delta_{1},\delta_{2},\delta_{3},\delta_{4}\right\} \). עכשיו מובטח לנו שעבור כל חלוקה \( P \) שמקיימת \( \lambda\left(P\right)<\delta \) וכל סכום רימן \( S_{P}^{z} \) שמתאים לה, \( \left|S_{P}^{z}-\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt\right|<\varepsilon \). זה מסיים את ההוכחה, ומרגיע אותי סופית. עכשיו מבחינתי זה בסדר גמור להגדיר אינטגרל מרוכב על ידי \( \int_{C}f\left(z\right)dz=\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt \) ותו לא. סוף טוב הכל טוב!