נוסחת קיילי לספירת עצים

הפוסט הזה בא לסגור חור שגילתי להפתעתי שקיים בבלוג: אין לי אף פוסט על אחת מהתוצאות החביבות עלי בקומבינטוריקה בסיסית - נוסחת קיילי לספירת עצים. הנוסחה אומרת שמספר העצים על קבוצה של \( n \) צמתים מסומנים היא \( n^{n-2} \), כך שקל לתאר אותה - אבל מה זה “עץ על קבוצה של צמתים מסומנים”? את זה יהיה קל להסביר. יותר מעניין להראות הוכחה לטענה הזו, והוכחה כזו כבר מתחבאת בשוליים של אחד הפוסטים שלי, אבל אני רוצה להראות הוכחה שונה מהותית שאני מאוד אוהב וממחישה טובה “מה הולך פה”.

אז בואו נדבר על מה הולך פה.

ראשית, גרפים. גרף \( G \) במובן שעליו אנחנו מדברים כאן מורכב מקבוצה \( V \) שלאיברים שלה קוראים צמתים וקבוצה \( E \) של זוגות של צמתים שנקראת קשתות. יש הרבה סוגים של גרפים, ובפוסט הזה אני אתעסק עם סוג פשוט למדי - לקשתות אין כיוון, ואין קשת מצומת לעצמו, ואין יותר מקשת אחת בין זוג צמתים. אפשר לחשוב על הקשתות בתור דרך לתאר קשר שיש או בין כל שני איברים שונים של הגרף.

גרפים הם משהו מאוד שימושי. שתי דוגמאות פשוטות: אנחנו יכולים למדל מפה באמצעות גרף - כל צומת הוא מיקום מעניין, וקשת אומרת שיש דרך ישירה לעבור בין שני מיקומים. או שאפשר לתאר רשת חברתית באמצעות גרף - כל משתתף ברשת הוא צומת, ויש קשת בין שני משתמשים שהם חברים (יש רשתות שבהן אפשר לעקוב אחרי מישהו שלא עוקב אחרייך; זה מתאים למושג של גרף מכוון שאני לא מדבר עליו כאן). עכשיו, אם יש לנו גרף אפשר “לטייל” עליו - להתחיל בצומת אחד וללכת לאורך קשתות כדי להגיע לצמתים אחרים. אם אני יכול להגיע מכל צומת לכל צומת בגרף, אומרים שהוא קשיר. זה מוביל אותי למושג של עץ, שאני אגדיר פה בצורה שנוחה לי - עץ הוא גרף קשיר שהוא מינימלי במובן זה שכל קשת שנסיר ממנו, תהפוך אותו לבלתי-קשיר. אפשר לחשוב על זה גם כך - אין בגרף “מעגלים”, אבל אני לא אגדיר פורמלית מה זה מעגל. הנה דוגמא לאיך זה נראה:

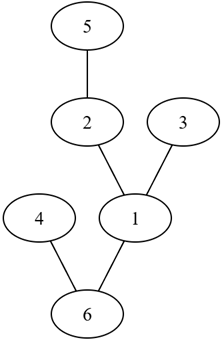
עכשיו, כשאני אומר שהצמתים הם מסומנים אני אומר שאני יכול להבדיל בין שני צמתים שונים. זה נשמע כמעט טריוויאלי, אז בואו נראה דוגמא:

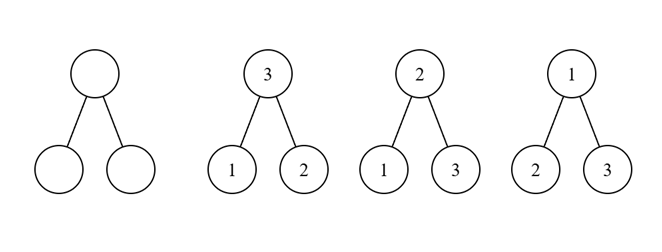
יש לנו כאן איור של עץ פשוט במיוחד (למעשה, הוא “שרוך”) אבל כשיש לנו סימונים לצמתים, אנחנו רואים שבעצם יש כאן שלושה עצים שונים, כתלות בשאלה מי הצומת שנמצא באמצע. זו סיטואציה שיותר קל לספור מאשר הסיטואציה שבה אין לנו סימנים על הצמתים ולא אדבר עליה בכלל בפוסט.

שלושת העצים שראינו פה הם המקרה של נוסחת קיילי עבור \( n=3 \). עבור \( n=4 \) הנוסחה אומרת לנו שכבר צפויים \( 4^{2}=16 \) עצים, אבל זו כבר תהיה מהומה לצייר את כולם, ומבט חטוף בהם לא מראה סדר כל כך ברור שאפשר לנצל. אז איך בדיוק להוכיח את הנוסחה? יש כמה גישות שונות להוכחה אבל זו שאני אוהב משתמשת במה שנקרא סדרות Prüfer. הרעיון פה הוא שאפשר לקודד כל עץ על קבוצת הצמתים \( V \) כך ש-\( \left|V\right|=n \) באמצעות סדרה מאורך \( n-2 \) של איברים מ-\( V \), או כמו שאוהבים לסמן לפעמים כשחושבים על האיברים של \( V \) בתור “אותיות” ועל הסדרה בתור “מילה”, באמצעות סדרה ב-\( V^{n-2} \). הרעיון הוא זה: ככל שאיבר מופיע יותר פעמים בסדרה, כך יש לו יותר שכנים, וכל פעם שבה הוא מופיע בסדרה אומרת “אוקיי, אחד מהשכנים של הצומת הזה כבר לא יהיה רלוונטי להמשך אז אפשר לשכוח ממנו”. זה קצת אמורפי אז הנה מה שעושים באופן כללי כדי לבנות מילה ב-\( V^{n-2} \) מתוך העץ \( G=\left(V,E\right) \).

ראשית, בואו נקבע סדר כלשהו על הצמתים של \( V \), נאמר \( V=\left\{ v_{1},v_{2},\ldots,v_{n}\right\} \). לסדר יש חשיבות; אם נסדר את אברי הקבוצה בצורה שונה, אז אותו עץ יניב מילים שונות. אז נתייחס לסדר בתור משהו נתון.

עכשיו, אם \( \left|V\right|=2 \) אין לנו בכלל מה לעשות - יש עץ יחיד על שני צמתים, שמורכב משניהם מחוברים בקשת (הם חייבים להיות מחוברים או שהגרף לא יהיה קשיר ולכן לא עץ). אז במקרה הזה, המילה שלנו (שאמורה להיות מאורך \( n-2=0 \)) היא מה שמכונה “המילה הריקה”, מילה בלי אותיות בכלל שמסומנת ב-\( \varepsilon \).

כשיש יותר משני צמתים, נרצה למצוא צומת שהסרה שלו מהעץ עדיין תשאיר עץ, ולהסיר אותו. בשביל שהסרה של צומת לא תקלקל את העציות של העץ, הצומת הזה צריך להיות מבוי סתום, נקודת קצה של העץ - כלומר, להיות מחובר רק לצומת יחיד. אנחנו אומרים שהדרגה של צומת היא מספר הקשתות שמחוברות אליו, אז מה שאנחנו מחפשים הוא צומת מדרגה 1. לצמתים כאלו יש שם מיוחד: עלה (כי עלה הוא “נקודת קצה” של עץ). יכולים להיות כמה עלים בגרף - אז נבחר מתוכם את הקטן ביותר, על פי הסדר שיש על הצמתים. השאלה האמיתית, כמובן, היא למה תמיד קיים עלה; אני אראה את זה בהמשך.

עכשיו, אחרי שבחרנו את העלה הקטן ביותר אנחנו מסירים אותו מהעץ ומוסיפים למילה שאנחנו בונים - לא את הסימון של העלה שהסרנו, אלא דווקא את הסימון של השכן היחיד שלו. למה? כי כשנשחזר את העץ מתוך המילה נוכל לדעת בודאות מי העלה שהוסר בשלב הזה בזכות הקטע הזה של “הקטן ביותר” - המידע החסר דווקא יהיה מי השכן שלו, וזה מה שהמילה תגיד לנו.

וזהו, זה כל מה שעושים; חוזרים על זה \( \left|V\right|-2 \) פעמים עד שנשארים עם שני צמתים ובסיטואציה הזו כפי שכבר ראינו לא צריך לטפל. אז האלגוריתם, על קלט \( G=\left(V,E\right) \), הוא:

1. אתחלו \( w=\varepsilon \).
2. אם \( \left|V\right|=2 \) סיימו והוציאו את \( w \) כפלט.
3. מצאו מבין כל העלים של \( G \) את הצומת המינימלי. סמנו אותו ב-\( v \) ואת הקשת היחידה שמחוברת אליו ב-\( \left(v,u\right) \).
4. הוסיפו את \( u \) ל-\( w \): \( w\leftarrow w\cdot u \).
5. הסירו מ-\( G \) את \( v \) ואת הקשת \( \left(v,u\right) \).
6. חזרו לשלב 2.

בואו נראה איך זה יעבוד על העץ שהראיתי קודם, זה:

בתחילת הריצה, העלים הם \( \left\{ 3,4,5\right\} \) ומביניהם המינימלי הוא 3, לכן נתחיל בלהסיר אותו מהעץ ולכתוב \( 1 \) במילה. עכשיו, גם אחרי שהסרנו את 3 מהעץ, 1 עדיין לא הפך לעלה בעצמו, לכן קבוצת העלים שלנו עכשיו היא \( \left\{ 4,5\right\} \) ולכן אנחנו מסירים את 4 מהעץ וכותבים \( 6 \) במילה שלנו, שכרגע נראית ככה: \( 16 \). עכשיו, הסרת 4 הפכה את \( 6 \) לעלה בעצמו אז הקבוצה שלנו היא \( \left\{ 5,6\right\} \) אבל על פי הכללים שלנו, אנחנו מסירים קודם כל את \( 5 \) מהעץ ולכן מוסיפים למילה את \( 2 \) ומקבלים \( 162 \). זה הופך את \( 2 \) לעלה, כלומר קבוצת העלים שלנו כרגע היא \( \left\{ 6,2\right\} \) ומכיוון ש-\( 2 \) הוא הקטן יותר אנחנו מסירים אותו, כותבים \( 1 \) במילה ומסיימים - נשארנו רק עם הצמתים \( 1,6 \) וקיבלנו את המילה \( 1621 \).

זה היה מאוד נחמד - אנחנו מבינים איך האלגוריתם עובד, אבל עדיין צריך להראות שהוא עובד, כלומר שהוא נותן לנו התאמה חח”ע ועל בין עצים עם \( n \) צמתים ובין מילים מאורך \( n-2 \) מעל אלפבית מגודל \( n \). בשביל זה אני צריך להוכיח את הטענה הבאה: שלכל מילה \( w \) קיים עץ יחיד שהאלגוריתם מייצר את \( w \) ממנו. אבל לפני שאני אנסח את זה פורמלית ואוכיח את זה, בואו ננסה לקבל תחושה של מה קורה כאן על ידי זה שנסתכל על ה-1621 שקיבלנו ונשאל את עצמנו איך אפשר “לשחזר” את העץ המקורי ממנו. כלומר, נחשוב באופן לא פורמלי איך יעבוד אלגוריתם בכיוון ההפוך לזה שכבר ראינו.

מה שהאלגוריתם מקבל כקלט הוא את המילה \( w=1621 \) אבל גם את הקבוצה \( V=\left\{ 1,2,3,4,5,6\right\} \) של הצמתים של הגרף, יחד עם הסדר עליהם - הרי מהמילה בלבד הוא לא יכול להיות בטוח לגבי הסדר, ולא כל הצמתים בעץ בהכרח יופיעו במילה, אז צריך לספר לו את המידע הזה במפורש.

האלגוריתם מתחיל בלהסתכל על ה-1 השמאלי של \( 1621 \) ואומר לעצמו “הממ… אני יודע שהצומת הראשון שהסירו מהגרף היה שכן של 1, אבל מי הוא עצמו היה? הוא היה העלה בעל המספר המינימלי בשלב הזה, אבל מי היו העלים בהתחלה?”

זו שאלה טריקית, עד ששמים לב לעובדה הקריטית הבאה: במילה \( 1621 \) לא מופיעים עלים. שלושת הצמתים שמופיעים פה: \( 1,2,6 \), כולם היו מדרגה גבוהה מ-1. \( 2,6 \) היו מדרגה 2 ו-\( 1 \) היה מדרגה 3 ו… שימו לב שבמילה \( 1 \) מופיע פעמיים ואילו \( 2,6 \) מופיעים פעם אחת. אם נסתכל על עוד דוגמאות דומות, מהר מאוד נוכל להעלות השערה כללית: שמספר הפעמים שבהן צומת \( v \) מופיע במילה שווה לדרגה שלו פחות 1, \( d\left(v\right)-1 \). בפרט עלים לא מופיעים בכלל.

למה זה קורה? זה די פשוט, האמת. בכל פעם שבה צומת מופיע במילה, זה אומר שזה עתה הורדנו מהגרף את אחד מהשכנים שלו, כלומר הקטנו את הדרגה שלו ב-1. הפעם היחידה שבה אנחנו מקטינים את הדרגה של צומת ב-1 אבל לא מוסיפים אותו למילה היא כשהוא עצמו הצומת שמוסר מהגרף. מצד שני, בסיום ריצת האלגוריתם כל צומת הוסר מהגרף (ואז הוא נכתב \( d\left(v\right)-1 \) פעמים), או (במקרה של שני הצמתים האחרונים שנשארו) הפך להיות מדרגה 1, כלומר הדרגה שלו הוקטנה \( d\left(v\right)-1 \) פעמים ולכן הוא נכתב במילה \( d\left(v\right)-1 \) פעמים.

מה המסקנה? ראשית, שעל ידי הסתכלות ב-\( 1621 \) אני יודע שהעלים של הגרף הם \( 3,4,5 \), ושהם היו עלים במשך כל ריצת האלגוריתם. הקטן מביניהם הוא 3, כך שאני יכול להסיק שבצעד הראשון 3 הוסר מהגרף והשכן שלו היה הצומת הראשון שמופיע ב-\( 1621 \). לכן הדבר הראשון שאעשה יהיה להוסיף לגרף את הקשת \( \left(1,3\right) \) ואסמן לעצמי שכבר טיפלתי בצומת \( 3 \).

מכיוון שקראתי את האות הראשונה ב-\( 1621 \) אפשר להסיר אותה, להישאר עם המילה \( 621 \) ולחזור על מה שעשינו גם איתה. אותו הגיון יעבוד עכשיו גם עם 4, ולכן אני אסמן לעצמי שיש בגרף את \( \left(4,6\right) \) ואוריד את 4 מרשימת הצמתים שצריך לטפל בהם. אבל עכשיו קורה משהו מעניין - אני נשאר עם המילה \( 21 \) שבה \( 6 \) לא מופיע יותר. זה מספר לי שבשלב הזה של האלגוריתם המקורי, 6 היה עלה. לכן אני מוסיף אותו לקבוצת העלים הפוטנציאליים שלי, שכוללת עכשיו את \( 5,6 \). מכיוון ש-5 הוא עם האינדקס הקטן יותר, אני אחבר אותו ל-2 שבתחילת המילה. אחר כך אני נשאר עם המילה \( 1 \) שבה גם \( 2 \) לא מופיע, אז אוסיף גם אותו לרשימת הצמתים שצריך לבדוק, ומכיוון שהוא קטן מ-2 הוא יהיה הצומת שאני מחבר ל-1.

בשלב הזה נגמרה לי המילה, ונשארו רק שני צמתים שלא טיפלתי בהם: \( 1,6 \). אז אני מוסיף קשת גם להם ומסיים את הסיפור.

יופי, זה היה תיאור לא פורמלי של איך עובד האלגוריתם שמשחזר את העץ מתוך \( w \). עוד מעט אני אכתוב אותו בצורה פורמלית, אבל לפני כן בואו ננסה להבין איך מוכיחים את הטענה שרציתי להראות על כך שבהינתן \( w \) קיים עץ יחיד שנותן את \( w \). הניסוח הפורמלי של הטענה צריך להיות קצת יותר זהיר - כפי שראינו, אני חייב להתחיל מקבוצה \( V \) קונקרטית. נסמן \( \left|V\right|=n \) ועכשיו ניקח מילה \( w\in V^{n-2} \) והטענה היא שקיים ויחיד עץ עם קבוצת הצמתים \( V \) שנותן את \( w \).

אני אוכיח את הטענה באינדוקציה על \( n \), כשהבסיס הוא \( n=2 \). במקרה הזה, \( w\in V^{0} \) חייבת להיות המילה הריקה \( \varepsilon \), ואילו \( V \) היא קבוצה בת שני צמתים. יש בדיוק שני גרפים על שני צמתים: הגרף שבו הם לא מחוברים בקשת שאינו עץ ולכן אינו רלוונטי לדיון; והגרף שבו הם כן מחוברים והוא כן עץ והוא אכן מחזיר \( \varepsilon \) על פי האלגוריתם שראינו קודם. אז את הבסיס יש לנו.

בשביל הצעד, ניקח את \( w \) ונפרק אותה לאות הראשונה וכל היתר: \( w=\sigma w^{\prime} \) כך ש-\( w^{\prime}\in V^{n-3} \). ה-\( \sigma \) הזה הוא הצומת הפנימי של הגרף שאליו מחובר העלה שאנחנו רוצים “לשחזר” בשלב הזה, אבל מי זה העלה הזה? זו הנקודה שדיברתי עליה, שבה אפשר לגלות את העלה גם בלי שהוא יהיה כתוב לנו במפורש: נשים לב שב-\( V \) יש יותר צמתים מאשר יש אותיות ב-\( w \) אז בהכרח קיימים צמתים ב-\( V \) שלא מופיעים ב-\( w \) בכלל, ולכן הם עלים בכל עץ שנותן את \( w \), כפי שראינו, ונסמן את המינימלי מביניהם ב-\( u \). מה שקרה פה הוא שבכל עץ שנותן את \( w \), בהכרח \( u \) מחובר אל \( \sigma \), כי בשלב הראשון של האלגוריתם \( u \) בהכרח היה מוסר (הוא המינימלי מבין העלים של כל עץ שנותן את \( w \)) והוא בהכרח מחובר אל \( \sigma \) בכל עץ שמחזיר את \( w \) כי האות הראשונה ב-\( w \) היא \( \sigma \).

עכשיו אפשר להשתמש בהנחת האינדוקציה. נגדיר \( V^{\prime}=V\backslash\left\{ u\right\} \), כלומר הסרנו את \( u \) מתוך \( V \), וקיבלנו קבוצה מגודל \( n-1 \) ומילה \( w^{\prime}\in V^{\prime\left(n-1\right)-2} \) (אנחנו יודעים ש-\( w^{\prime} \) אכן מורכבת רק מאיברים של \( V^{\prime} \) כי \( w \) הורכבה מאיברים של \( V \), והסרנו מ-\( V \) רק איבר שלא הופיע ב-\( w \)). על פי הנחת האינדוקציה קיים עץ יחיד שנותן את \( w^{\prime} \) הזו, ואחרי שנצרף אליו את הקשת \( \left(u,\sigma\right) \) שחייבת להיות בכל עץ שנותן את \( w \) נקבל עץ יחיד שנותן את \( w \).

בואו נכתוב את מה שעשינו בתור אלגוריתם מסודר. על קלט של קבוצה \( V \) ומילה \( w\in V^{\left|V\right|-2} \), האלגוריתם פועל כך:

1. מאתחל קבוצת קשתות \( E\leftarrow\emptyset \) וקבוצת "צמתים לטיפול" \( S\leftarrow V \) ומפרק את המילה לאותיות \( w=\sigma_{1}\ldots\sigma_{n-2} \).
2. לכל \( i=1,2,\ldots,n-2 \):
1. מוצא את האיבר הקטן ביותר של \( S \) שלא מופיע ב-\( \sigma_{i}\ldots\sigma_{n-2} \) ומסמן אותו ב-\( u \).
2. \( E\leftarrow E\cup\left\{ \left(u,\sigma_{i}\right)\right\} \)
3. \( S\leftarrow S\backslash\left\{ u\right\} \)
3. בשלב הזה \( S=\left\{ u,v\right\} \). מבצע: \( E\leftarrow E\cup\left\{ \left(u,v\right)\right\} \)
4. מחזיר את \( E \).

זה הכל! מה שחמוד פה הוא שההתאמה למילות פרופר היא שימושית קצת יותר מאשר רק הוכחת המשפט הזה. למשל, אם אני רוצה לבנות עץ עם מבנה ספציפי, שבו יש צומת אחד מדרגה 7 וארבעה מדרגה 3 והיתר עלים, אני יודע בדיוק מה לעשות - מילה עם אות אחת שחוזרת על עצמה 6 פעמים ועוד ארבע אותיות שכל אחת חוזרת על עצמה פעמיים. אני יכול להגריל מילים תחת האילוצים הללו (זה קל, זו בסך הכל פרמוטציה אקראית של סימובלים) ולקבל עץ אקראי שעונה לדרישה המקורית שלי. זה ממש נחמד! הרבה יותר שווה מסתם לדעת את \( n^{n-2} \).