מונה מבוכים

מה אנחנו מנסים לעשות פה בכלל

בפוסט הזה אני רוצה לדבר על משהו שהוא בין חידה לבין תוצאה מתמטית ישירה יחסית, אבל כזו שהיא ממש נחמדה בזכות שילוב של שני דברים: ראשית, זו בעיה מספרית קונקרטית עם פתרון קונקרטי, וכזה שזועק בכל הכוח "אין לכם שום סיכוי למצוא אותי בלי להיות חכמים!" ושנית, זו חידה שנותנת הזדמנות לראות כמה וכמה פיסות יפות של מתמטיקה שמשתלבות נהדר ביחד כדי לפתור אותה. והחידה היא זו: כמה מבוכים מגודל \(423\times855\) יש?

כמובן, נצטרך להסביר את זה קצת.

ראשית, מבוכים יש משלל סוגים ומינים. אני מדבר על סוג מאוד קונקרטי - מבוכים שנראים ככה:

במבוכים כאלו, ה"עולם" שלנו הוא לוח דו ממדי של \(n\times m\) תאים ריבועיים. לכל תא יש ארבעה שכנים (למעלה/למטה/ימינה/שמאלה) למעט אלו שבקצוות, ובין כל שני שכנים או שיש קיר, או שאין קיר. בשביל שמשהו יהיה "מבוך" צריך שיהיה בדיוק מסלול יחיד בין כל שני תאים - כך שמצד אחד אפשר להגיע מכל מקום לכל מקום, ומצד שני אין לנו שתי דרכים שונות להגיע לאותו מקום. אפשר לחשוב על זה ככה - מבוך כזה ממקסם את מספר הקירות שיש בו תוך שמירה על התכונה שאפשר להגיע בו לכל מקום.

הנה דוגמא לכל 15 המבוכים הקיימים מגודל \(3\times2\) :

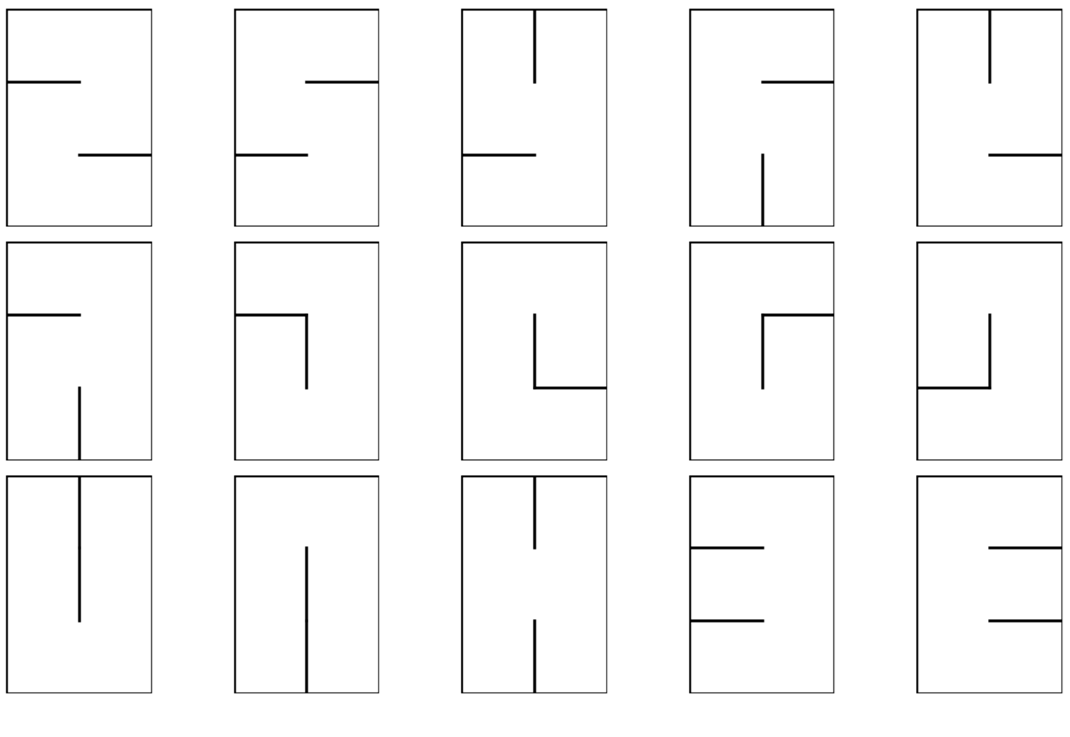
אם כן, עבור גודל \(n\times m\) עבור \(n,m\) שרירותיים, איך סופרים כמה מבוכים יש? נתחיל מהשיטה הכי נאיבית; הרבה פעמים הגישה הנאיבית עובדת מספיק טוב בפועל ולא צריך לחשוב יותר מדי. לא הפעם. בגישה הנאיבית כאן, אפשר לבנות רשימה של כל הקירות הפוטנציאליים, ולכל תת-קבוצה של קירות לבדוק אם קיבלנו מבוך או לא, ואם כן להוסיף אותו לספירה. כמה קירות פוטנציאליים יש? אם נסתכל על השורה העליונה של המבוך, היא כוללת \(m\) תאים שמופרדים ב-\(m-1\) קירות אנכיים, אז יש \(n\left(m-1\right)\) קירות אנכיים בכל המבוך ובאופן דומה יש גם \(m\left(n-1\right)\) קירות אופקיים, כלומר בסך הכל יש \(2mn-\left(n+m\right)\) קירות. אם אנחנו רק רוצים לקבל אינטואיציה אפשר להניח ש-\(n,m\) הם בערך מאותו סדר גודל ולהשתמש בסימן \(O\) שבמדעי המחשב אוהבים להשתמש בו כדי להגיד "בערך"(בערך... למעשה \(\Theta\) הוא סימון יותר מדויק כאן אבל למי אכפת) ולהגיד שיש לנו סדר גודל של \(O\left(n^{2}\right)\) קירות. עכשיו, אם \(A\) היא קבוצה אז יש לה \(2^{\left|A\right|}\) תת-קבוצות אז יש לנו \(O\left(2^{n^{2}}\right)\) מבוכים פוטנציאליים, ועבור כל אחד כזה צריך לבדוק אלגוריתמית שבאמת קיבלנו מבוך... זה לא יילך, יש מספר אקספוננציאלי של מבוכים פוטנציאליים ובדיקה שמשהו היא מבוך תשתמש באלגוריתם חיפוש כמו DFS שלוקח \(O\left(n^{2}\right)\) זמן (לפחות כמספר התאים, הרי הוא צריך לבקר בכולם). בקיצור, לא לא לא. הפתרון הנאיבי לא קשור למציאות פה.

אבל יש מושג שהכנסה שלו לתמונה מייד מפשטת את כל הסיפור - עץ. הצגתי את המושג הזה בעבר בבלוג ספציפית מתוך הדוגמא של בניית מבוכים, אז אפשר להבין שאני אוהב את הנושא הזה - אבל שימוש בעצים לתאר מבוכים הוא רק קצה-קצהו של תחום עצום של כל הדברים שעצים משמשים להם. הנה התקציר: עץ הוא מקרה פרטי מעניין של מה שנקרא גרף, כשגרף הוא משהו שכולל אוסף של "צמתים" כך שכל שני צמתים יכולים להיות מחוברים בקשת, או לא מחוברים בקשת. אצלנו אפשר לחשוב על מבוך בתור גרף שבו התאים הם הצמתים, ויש קשת בין שני תאים סמוכים שלא מופרדים בקיר.

המושג של "אפשר להגיע מכל תא לכל תא" מתורגם לתורת הגרפים בתור האמירה ש"הגרף קשיר" , והקטע הזה שאין שתי דרכים שונות להגיע מנקודה א' לנקודה ב' מתואר בתור "הגרף חסר מעגלים" . ההגדרה הפורמלית של עץ היא בתור "גרף קשיר וחסר מעגלים" . אלו שתי תכונות שהן מנוגדות זו לזו במובן מסוים - ככל שמוסיפים קשתות כך אנחנו מגדילים את הסיכוי שהגרף יהיה קשיר אבל מקטינים את הסיכוי שהגרף יהיה חסר מעגלים, וההפך. לכן הנקודה שבה שתי התכונות הללו מתקיימות בו זמנית היא קסומה למדי (יש סיטואציה דומה מאוד באלגברה לינארית שבה קבוצת וקטורים יכולה להיות בלתי תלויה לינארית ויכולה להיות פורשת וכששתי התכונות הללו מתקיימות בו זמנית אנחנו מקבלים את המושג הקסום של בסיס; הדמיון הזה לא מקרי ושתי הסיטואציות הללו מוכללות על ידי מושג שנקרא מטרואיד, אבל נעזוב את זה).

אחד הדברים הנחמדים שאפשר להוכיח על עץ הוא שאם העץ כולל \(n\) צמתים, אז הוא כולל בדיוק \(n-1\) קשתות - כל קשת שנוסיף תיצור מעגל, וכל הסרת קשת תקלקל את הקשירות. מה שזה אומר לנו הוא שמלכתחילה אין טעם לבדוק את כל תתי-הקבוצות של הקירות האפשריים; במבוך שלנו יש \(nm\)
תאים אז אנחנו צריכים להסתכל רק על תת-קבוצות מגודל \(nm-1\) של קבוצת כל הקירות האפשריים ולהסיר רק את הקירות הללו. העניין הוא שמספר תתי-הקבוצות הללו הוא... עדיין אקספוננציאלי. התיאוריה הבסיסית של עצים חוסכת לנו חלק מהעבודה, אבל לא חלק גדול במיוחד. צריך להוסיף משהו חזק יותר.

המשהו החזק יותר נקרא "משפט המטריצה-עץ של קירקהוף" והוא לטעמי תוצאה יפהפיה ממש. יש לי כבר פוסט עליו שבו אני גם מוכיח אותו, אז פה מן הסתם אוותר על ההוכחה (הלא פשוטה אבל היפה מאוד בזכות עצמה). הרעיון פה הוא שאיכשהו אפשר להמיר את הבעיה של ספירת עצים לבעיה מתחום האלגברה הלינארית, של חישוב דטרמיננטה של מטריצה מסוימת שנבנית מתוך הגרף שלנו. חישוב דטרמיננטה הוא דבר קל יחסית מבחינה חישובית; והפוסט הזה יעסוק בעיקר באיך עבור הסיטואציה הספציפית שלנו של דטרמיננטה של מטריצה שהגיעה מגרף שהוא עץ שנבנה בצורה שמתאימה למבוך החישוב הזה אפילו עוד יותר קל מאשר בדרך כלל.

אז איך המשפט הולך? ראשית, מה שהמשפט עושה הוא לספור עצים פורשים של גרף נתון. הרעיון בעץ פורש הוא לקחת גרף שהוא כבר קשיר, ולהסיר ממנו קשתות עד שהוא הופך גם לחסר מעגלים (כלומר הוא עץ, והוא "פורש את הגרף" במובן זה שהוא על אותה קבוצת צמתים כמו הגרף המקורי ומשתמש בקשתות מתוך הגרף המקורי). אפשר להראות שלא משנה איך מסירים קשתות, כל עוד השיטה היא "תמצאו קשת שהסרה שלה לא פוגעת בקשירות של הגרף ותעיפו אותה עד שאין יותר כאלו" היא תמיד תחזיר עץ, אבל לפעמים יש עצים פורשים שהם יותר מעניינים; למשל, אם יש על הקשתות משקלים ואנחנו רוצים למצוא עץ פורש שהמשקל הכולל של הקשתות שלו הוא מינימלי, זו הזדמנות לשלוף את האלגוריתמים של קרוסקל ופרים שאוהבים להראות בקורס מבוא לאלגוריתמים ומוצאים עץ מינימלי שכזה בצורה לא רעה בכלל.

במקרה שלנו אנחנו לא רוצים למצוא עץ פורש אלא לספור כאלו, והגרף שאנחנו רוצים למצוא עצים פורשים שלו הוא הגרף שמתאר את המבוך כשאין בו בכלל קירות - כלומר, כשיש בו את כל הקשתות האפשריות. זה לא אומר שכל שני צמתים בגרף יהיו מחוברים בקשת - תזכרו, מלכתחילה קשת יכולה להיות רק בין תא במבוך ובין ארבעת השכנים שלו (או פחות שכנים, אם הוא בקצה כלשהו של המבוך וחלק מהשכנים חסרים). זה אומר שמלכתחילה, הגרף הוא "דליל" יחסית - רוב זוגות הצמתים לא הולכים להיות מחוברים בקשת, ולמעשה הדרגה של כל צומת (מספר הקשתות שמחוברות אליו) מראש מוגבלת על ידי מספר נמוך יחסית (4) שבכלל לא תלוי בגודל הגרף. ועוד יותר מכך - לגרף יש מבנה נחמד שמגיע מכך שהוא מתקבל ממבוך שנראה נחמד, עם יחסי שכנות די מסודרים. בשלב הראשון לא נשתמש בזה, אבל בהמשך בהחלט כן.

אני אניח שאנחנו יודעים מה זו מטריצה. אם לא, יש לי פוסטים בנושא ואפשר פשוט לחשוב עליה בתור טבלה של מספרים, אבל לא אכנס כאן להגדרות הפורמליות שלה.

בשביל משפט המטריצה-עץ אנחנו מגדירים מטריצה שנקראת לפלסיאן של גרף. אם \(G=\left(V,E\right)\) הוא הגרף שלנו, עם קבוצת צמתים \(V=\left\{ v_{1},\ldots,v_{n}\right\}\) וקבוצת קשתות \(E\) , אז מטריצה די טבעית שנהוג להגדיר עבור \(G\) היא מטריצת השכנויות של \(G\) : מטריצה \(A_{G}\) כך ש-\(\left[A_{G}\right]_{ij}=\begin{cases} 1 & \left(v_{i},v_{j}\right)\in E\\ 0 & \left(v_{i},v_{j}\right)\notin E \end{cases}\) . כלומר, אם יש קשת בין \(v_{i},v_{j}\) אז כתוב בה 1 ואחרת כתוב בה 0. את זה אפשר להכליל די בקלות - אם בגרף שלנו מרשים שיותר מקשת אחת תחבר כל זוג צמתים (מה שמגדיל את מספר העצים הפורשים, כי אפשר פעם לבחור אחת מהקשתות הללו ופעם קשת אחרת) אז במקום לכתוב 1 פשוט נכתוב את מספר הקשתות שיש בין \(v_{i},v_{j}\) . עוד פישוט שאני אעשה יהיה להניח ש-\(A_{ii}=0\) תמיד, כלומר שאין קשת שמחברת צומת לעצמו ("חוג עצמי") - בהחלט יכולות להיות קשתות כאלו בגרף כללי, אבל בהקשר של ספירת עצים פורשים הן לא רלוונטיות כי כל קשת כזו יוצרת מעגל ולכן הן לא יהיו באף עץ פורש, ולכן אם רוצים שנמצא את מספר העצים הפורשים בגרף נתון, הוא יהיה שווה למספר העצים הפורשים באותו הגרף אחרי שהוסרו ממנו החוגים העצמיים, ולכן אפשר לבצע את ההנחה הזו "בלי הגבלת הכלליות" , כפי שנהוג לומר.

מטריצת השכנויות הזו היא לא הלפליסאן, בשביל זה נצטרך להגדיר עוד מטריצה שגם היא לא הלפלסיאן: מטריצת הדרגות \(\Delta_{G}\) שהיא מטריצה אלכסונית כך ש-\(\Delta_{ii}=d\left(v_{i}\right)\) , כלומר היא מספר הקשתות שמחוברות אל \(v_{i}\) . עכשיו אפשר לשלב את שתיהן כדי לקבל את מה שהוא כן הלפלסיאן:

\(L_{G}=\Delta_{G}-A_{G}\) , כלומר זו המטריצה שבאלכסון שלה כתובות דרגות הצמתים, ובכל כניסה אחרת כתוב מינוס מספר הקשתות שמחברות שני צמתים נתונים.

אם ננסה לחשב את הדטרמיננטה (הנה הפוסט שלי על מה זו דטרמיננטה) של המטריצה הזו נגלה להפתעתנו הרבה שמקבלים 0... לא הבטחתי שנקבל את מספר העצים הפורשים? ובכן, לא, אבל הנה מה שעושים - בוחרים צומת שרירותי \(v_{i}\) , מסלקים מהמטריצה את השורה והעמודה ה-\(i\) (זה אומר שלוקחים מינור של המטריצה) ואז מחשבים את הדטרמיננטה - בסיטואציה הזו נקבל תמיד את אותה תוצאה בלי תלות באיזה צומת הסרנו, והתוצאה הזו תהיה מספר העצים הפורשים של הגרף (במקרה שבו הגרף מכוון, שלא עליו אני מדבר, יש יותר משמעות לשאלה איזה \(v_{i}\) בוחרים - הספירה תהיה רק של העצים הפורשים ש-\(v_{i}\)
הוא השורש שלהם).

בואו נראה דוגמא לקסם הזה בפעולה, עבור המבוכים שלנו. כדי לשמור את העניינים עדיין סבירים בקושי, נסתכל על מבוך של \(2\times3\) . כבר ראינו קודם שקיימים 15 מבוכים כאלו על ידי זה שציירנו אותם במפורש. הנה מטריצת הלפלסיאן במקרה הזה:

\(L_{G}=\left(\begin{array}{cccccc} 2 & -1 & 0 & -1 & 0 & 0\\ -1 & 3 & -1 & 0 & -1 & 0\\ 0 & -1 & 2 & 0 & 0 & -1\\ -1 & 0 & 0 & 2 & -1 & 0\\ 0 & -1 & 0 & -1 & 3 & -1\\ 0 & 0 & -1 & 0 & -1 & 2 \end{array}\right)\)
בגלל שלוח של \(2\times3\) הוא ממש צפוף וכל תא נמצא בקצה כלשהו של המבוך, אנחנו לא רואים כל כך טוב פה את זה שעל האלכסון צפויים להיות בעיקר 4-ים ושבכל שורה ועמודה יהיו מעט יחסית \(-1\) -ים ובעיקר יהיו אפסים, אבל לא נורא. לחשב את הדטרמיננטה של המטריצה הזו זה טיפה כאב ראש אבל אפשר לעשות את זה עם דירוג מטריצות יחסית מהר (מודולו עשר שגיאות החישוב שיהיו לי בדרך) ומקבלים, כמה מפתיע, 15! אז המשפט עובד. כאמור, לא אוכיח את המשפט כי יש לי פוסט ייעודי עבור ההוכחה, אבל זה ממש ממש מגניב שזה עובד.

האם סיימנו? לא. כי לא שאלתי על \(2\times3\) . שאלתי על \(423\times855\) . במקרה הזה אני אצטרך מטריצה מסדר \(t\times t\) כאשר \(t=423\cdot855=361,665\) . זו כבר מטריצה די גדולה, ולחשב את הדטרמיננטה שלה יהיה כאב ראש אמיתי, שלא לדבר על כך שהדטרמיננטה צפויה להיות מספר עצום ולכן נצטרך לעבוד עם מספרים שמיוצגים בנקודה צפה, ולוודא שאין לנו שגיאות נומריות שמצטברות בחישוב של הדטרמיננטה... את כל אלו אפשר לעשות - יש תחום שלם ומפואר שעוסק בחישובים עם מטריצות דלילות ומספרים גדולים - אבל מה שיפה פה הוא שבמקרה הקונקרטי שלנו אפשר לנצל את המבנה המיוחד של הגרף שלנו כדי לפשט בצורה משמעותית ביותר את החישוב.

מה הולך ללכת כאן

עד עכשיו הבנו את כל המרכיבים העקרוניים של הפתרון, עכשיו אפשר להציג את הפתרון עצמו בלי יותר מדי הוכחות, ואז נגיע להוכחות עצמן (שהן כבדות יחסית ולכן עדיף לחכות איתן). ראשית, אם נסתכל על מטריצת הלפלסיאן \(L_{G}\)
ונסמן את הערכים העצמיים שלה ב-\(\lambda_{0},\lambda_{1},\ldots,\lambda_{t-1}\) (זו מטריצה מסדר \(t\times t\) ולכן יש לה \(t\) ערכים עצמיים) כך ש-\(\lambda_{0}=0\) הוא הערך העצמי 0 (אנחנו נראה ש-0 הוא תמיד ערך עצמי של \(L_{G}\) ) אז הדטרמיננטה של המינור שלה היא \(\frac{1}{t}\lambda_{1}\lambda_{2}\cdots\lambda_{t-1}\) . כלומר - אין צורך לחשב דטרמיננטה בכלל, מספיק למצוא את הערכים העצמיים.

שנית, הגרף \(G\) הוא לא סתם גרף אקראי, יש לו כאמור מבנה יפה - אפשר להציג אותו בתור מכפלה של שני גרפים פשוטים בהרבה. יש כמה סוגים של מכפלות של גרפים, והסוג שמתאים כאן נקרא מכפלת קופסה, \(G=G_{1}\square G_{2}\) , ונראה עוד מעט את הההגדרה שלו. זה מפשט את העניינים עבורנו כי אפשר להראות שאם הערכים העצמיים של \(L_{G_{1}}\) הם \(\tau_{0},\tau_{1},\ldots,\tau_{n-1}\)
והערכים העצמיים של \(L_{G_{2}}\) הם \(\rho_{0},\rho_{1},\ldots\rho_{m-1}\)
אז הערכים העצמיים של \(L_{G_{1}\square G_{2}}\) הם מהצורה \(\lambda_{kh}=\tau_{k}+\rho_{h}\)
עבור \(0\le k\lt n\) ו-\(0\le h\lt m\) . זה, והנוסחה של \(\frac{1}{t}\lambda_{1}\lambda_{2}\cdots\lambda_{t-1}\)
שראינו קודם, יאפשרו לנו להגיע למסקנה שמספיק לחשב את המכפלה

\(\prod_{k=1}^{m-1}\prod_{h=1}^{n-1}\left(\tau_{k}+\rho_{h}\right)\) (שימו לב שה-\(\frac{1}{t}\) נעלם והאינדקסים מתחילים מ-1 ולא מ-0; זה כמובן לא מקרי אלא הם יבטלו זה את זה איכשהו)

הגרפים \(G_{1},G_{2}\) שבהם נשתמש יהיו שרוכים, כלומר גרפים שהם בסך הכל מסלול ישר, אחד עם \(n\) צמתים ואחד עם \(m\) צמתים, שיסומנו \(P_{n},P_{m}\) . אלו גרפים כל כך פשוטים שאפשר לחשב בקלות יחסית את הערכים העצמיים שלהם, ואנחנו נשתמש במשהו שנקרא פולינומי צ'בישב כדי לקבל שהערך העצמי ה-\(k\) -י של \(P_{n}\) הוא \(4\cos^{2}\left(\frac{k\pi}{2n}\right)\) . מכאן נקבל את הנוסחה הסופית, שסופרת את מספר המבוכים מסדר \(n\times m\) :

\(T\left(n,m\right)=\prod_{k=1}^{n-1}\prod_{h=1}^{m-1}\left(4\cos^{2}\left(\frac{k\pi}{2n}\right)+4\cos^{2}\left(\frac{h\pi}{2m}\right)\right)\)
הנוסחה הזו אולי נראית קצת מפחידה, אבל היא פשוטה מאוד לחישוב בעזרת מחשב, גם עבור \(n=423,m=855\) . החלק הטריקי היחיד הוא שאנחנו נגררים להכפלה של מספרי ענק, וזה קשה למחשבים, אבל יש תעלול סטנדרטי שפותר את זה - לוקחים לוגריתם של הכל, והוא הופך את המכפלה לסכום, ואז לסיום לוקחים את התוצאה שמקבלים ומוציאים את האקספוננט שלה. גם את זה אני הולך להראות במפורש.

יפה, אז עכשיו אנחנו מבינים מה הולך לקרות, אבל עדיין נשארו ההוכחות המסודרות שיעזרו לנו להבין למה בעצם כל הקסם הזה עובד.

הדטרמיננטה של לפלסיאן

נתחיל עם מה שקל להראות - למטריצת הלפלסיאן יש ערך עצמי 0. בשביל לראות את זה בקלות בואו נחזור ללפלסיאן הדוגמא שלנו:

\(L_{G}=\left(\begin{array}{cccccc} 2 & -1 & 0 & -1 & 0 & 0\\ -1 & 3 & -1 & 0 & -1 & 0\\ 0 & -1 & 2 & 0 & 0 & -1\\ -1 & 0 & 0 & 2 & -1 & 0\\ 0 & -1 & 0 & -1 & 3 & -1\\ 0 & 0 & -1 & 0 & -1 & 2 \end{array}\right)\)
אם נסתכל על כל שורה, נראה שהיא מסתכמת ל-0. זה לא מקרי; על האלכסון בכניסה \(ii\) יש לנו את הדרגה של הצומת \(v_{i}\) , כלומר מספר הקשתות שמחוברות אליו. יתר השורה ה-\(i\) -ית כוללת, לכל צומת \(v_{j}\ne v_{i}\) , את המינוס של מספר הקשתות בין \(v_{i}\)
ו-\(v_{j}\) . עכשיו, כל קשת שמחוברת אל \(v_{i}\) מחוברת לצומת כלשהו וזה לא יכול להיות \(v_{i}\) עצמו כי הנחנו שבגרף שלנו אין חוגים עצמיים, ולכן סך כל השורה חוץ מהאיבר על האלכסון הוא מינוס מספר הקשתות שמחוברות של \(v_{i}\) , כלומר מינוס הדרגה שלו, ולכן בתוספת האיבר על האלכסון נקבל 0.

עכשיו, טריק ידוע מאלגברה לינארית הוא שאם כל השורות של מטריצה מסתכמות לאותו מספר \(\lambda\) בדיוק, אז \(\lambda\) היא ערך עצמי של המטריצה עם הוקטור העצמי

\(\left(\begin{array}{c} 1\\ 1\\ \vdots\\ 1 \end{array}\right)\)
את זה אפשר לבדוק בצורה ישירה: כופלים את המטריצה בוקטור הזה, ונקבל אותו עצמו כפול \(\lambda\) . במקרה שלנו, זה אומר ש-\(\lambda=0\) הוא ערך עצמי של המטריצה, כמו שהבטחתי.

עכשיו, אם יש לנו מטריצה ריבועית \(A\) כלשהי מעל שדה סגור אלגברית כמו \(\mathbb{C}\) (וזה המקרה שלנו) אז יש לה צורת ז'ורדן, כלומר קיימת מטריצה משולשית עליונה \(J\) ומטריצה הפיכה \(P\) כך ש-\(A=P^{-1}JP\) . יש הרבה מה לומר על המבנה של \(J\) ואני מדבר על זה כאן, אבל מה שאנחנו צריכים פה הוא רק את זה שהאלכסון של \(J\) כולל את כל הערכים העצמיים של \(A\) , ושהדטרמיננטה של מטריצה משולשית עליונה היא מכפלת אברי האלכסון. בנוסף, הכפליות של הדטרמיננטה נותנת לנו

\(\left|A\right|=\left|P^{-1}\right|\left|J\right|\left|P\right|=\left|J\right|\left|P\right|^{-1}\left|P\right|=\left|J\right|\) (כאן השתמשנו בקסם היפהפה שבו דטרמיננטה היא סך הכל מספר מרוכב, ומספרים מרוכבים מתחלפים בכפל, להבדיל ממטריצות).

כלומר, המסקנה היא שלכל מטריצה ריבועית \(A\) מסדר \(n\times n\) (לא רק מטריצת לפלסיאן) מעל שדה סגור אלגברית, הדטרמיננטה שלה היא מכפלת כל הערכים העצמיים שלה. בפרט עבור מטריצת הלפלסיאן ראינו ש-0 הוא ערך עצמי ולכן הדטרמיננטה שלה היא 0. אז האינפורמציה המעניינת צצה רק כשמוחקים שורה ועמודה ולוקחים את הדטרמיננטה של התוצאה, ואני טוען שאם זו השורה והעמודה ה-\(i\) -יות, אז הדטרמיננטה תצא \(\frac{1}{n}\lambda_{1}\cdots\lambda_{n-1}\) . אבל למה? זה לא נכון באופן כללי; אם למשל אני לוקח מטריצה אלכסונית עם \(\lambda_{0},\ldots,\lambda_{n-1}\) על האלכסון ומוריד את השורה והעמודה הראשונים, אז אני אקבל מטריצה אלכסונית עם \(\lambda_{1},\ldots,\lambda_{n-1}\)
על האלכסון ולכן דטרמיננטה \(\lambda_{1}\cdots\lambda_{n-1}\) . עבור מטריצות אחרות אני אקבל דטרמיננטות שונות. אז מה במבנה של הלפלסיאן מוסיף את הפקטור \(\frac{1}{n}\) הזה?

ובכן, יש כמה דרכים להוכיח את זה. דרך מתבקשת אחת היא להגיד - שמעו, הלפליסאן הזה הוא מטריצה סימטרית ולכן קיים לו לכסון אוניטרי ולהשתמש בכל מני להטוטים שדיברתי עליהם ממש לא מזמן. בהחלט אפשר לעשות את זה וזה כנראה גם יעבוד, אבל אני הולך לגשת לזה מכיוון שונה לגמרי שנראה לי במבט ראשון הזוי למדי, ולכן זה כיפי.

המושג שאני רוצה להכניס לתמונה הוא מה שנקרא המטריצה המצורפת (מה שנקרא באנגלית adjugate marix). יש לי פוסט שבו אני מזכיר את המושג הזה אבל בואו ניזכר. באופן כללי, אם יש לי מטריצה ריבועית \(A\) , אני יכול לעשות את הפעולה שכבר ראינו: למחוק את השורה ה-\(i\) והעמודה ה-\(j\) , ואז לקחת דטרמיננטה של התוצאה. אני אסמן את זה ב-\(\left|A^{ij}\right|\) . למספר הזה קוראים cofactor של \(A\) , ואם \(A\) היא מסדר \(n\times n\) אז יש לנו אחד כזה לכל \(1\le i,j\le n\) . כשמחשבים דטרמיננטה של \(A\) דרך אחרת לעשות את זה היא לבחור שורה קונקרטית, נאמר \(i\) , ואז לחשב את \(\left|A\right|=\sum_{j=1}^{n}\left(-1\right)^{i+j}\left|A^{ij}\right|\) . כלומר, צריך לקחת את כל ה-cofactor-ים שמתאימים לשורה הזו ולחבר ולחסר אותם לסירוגין, ואיכשהו באופן קסום זה נותן את הדטרמיננטה.

עכשיו, המטריצה המצורפת של \(A\) שמסומנת \(\text{adj}A\) היא מה שמקבלים כשלוקחים את כל ה-
\(\left(-1\right)^{i+j}\left|A^{ij}\right|\)
הללו ושמים את כולם בתוך מטריצה משל עצמם - אבל שימו לב, מטריצה שבה התפקידים של \(i,j\) הפוכים. פורמלית: \(\left[\text{adj}A\right]_{ji}=\left(-1\right)^{i+j}\left|A^{ij}\right|\) . למה ההיפוך הזה? כי זה מבטיח שתתקיים התכונה המאוד יפה

\(A\cdot\text{adj}A=\left|A\right|\cdot I\) שהוכחתי בפוסט שקישרתי אליו. במילים אחרות, \(\frac{\text{adj}A}{\left|A\right|}\)
היא ההופכית של \(A\) במקרה שהיא קיימת (ואם היא לא קיימת אז הכפל ב-\(\text{adj}A\) מחזיר 0). התכונה הזו מראה ש-\(\text{adj}A\) זה לא סתם משהו אקראי שהמצאנו כי שיעמם לנו, ועכשיו נראה איך המושג הזה שימושי לנו כדי לנתח את \(L_{G}\) .

בואו נסמן ב-\(\kappa\) את מספר העצים הפורשים של \(G\) . מה שמשפט קירקהוף מראה הוא ש-\(\left|L_{G}^{ii}\right|=\kappa\) ; את זה אני לא הולך להוכיח שוב, אבל אני רוצה לטעון שמתקיים משהו קצת יותר כללי: שגם אם מוחקים שורה ועמודה שלא מתאימות לאותו אינדקס מקבלים את \(\kappa\) כל עוד כופלים ב"תיקון" הרגיל, כלומר \(\left(-1\right)^{i+j}\left|L_{G}^{ij}\right|=\kappa\) . ואת זה אפשר לנסח בצורה הקומפקטית הבאה: \(\text{adj}L_{G}=\kappa J\) כאשר \(J\) כאן הוא הסימון הסטנדרטי למטריצה הריבועית (מאותו סדר כמו \(L_{G}\) ) שכולה 1-ים (לא לבלבל עם ה-\(J\) של ז'ורדן שהזכרתי קודם ולא נזדקק לה יותר בפוסט הזה). כלומר, \(\kappa J\) היא בסך הכל המטריצה שכל הכניסות שלה שוות \(\kappa\) . אני מקווה שברור למה - כי הכניסה ה-\(ji\) שלה היא \(\left(-1\right)^{i+j}\left|L_{G}^{ij}\right|=\kappa\) . כמובן, צריך להוכיח את זה; וזה כל העניין, שיהיה לי יותר קל להוכיח את זה על ידי עבודה ישירה מול \(\text{adj}L_{G}\) .

ראשית, צריך להפריד לשני מקרים על פי הדרגה של \(L_{G}\) (המימד של מרחב השורות/מרחב העמודות של \((L_{G}\) . כזכור, הדרגה \(\text{rank} L_{G}\) של מטריצה בפרט קובעת אם היא הפיכה או לא - אם למטריצה מסדר \(n\times n\) יש דרגה קטנה מ-\(n\) אז היא לא הפיכה, ולכן הדטרמיננטה שלה שווה לאפס. עכשיו, אנחנו כבר יודעים ש-\(L_{G}\) לא הפיכה ולכן הדרגה שלה קטנה מ-\(n\) , אבל אם מתקיים גם \(\text{rank} L_{G}\lt n-1\)
אז גם אחרי שנמחק מ-\(L_{G}\) שורה ועמודה עדיין נקבל מטריצה מדרגה קטנה מ-\(n-1\) כי אם אחרי המחיקה יש לנו קבוצה של \(n-1\) שורות בלתי תלויות, אז גם אחרי שנוסיף להן עוד כניסה עבור העמודה שמחקנו הן עדיין יהיו בלתי תלויות וגם אם נוסיף למטריצה שורה חדשה הן עדיין יהיו בלתי תלויות, ולכן יוצא שכבר במטריצה המקורית הדרגה הייתה \(n-1\) . אז הגענו לכך שאחרי המחיקה תהיה לנו מטריצה מסדר \(n-1\) שהדרגה שלה קטנה מ-\(n-1\) ולכן הדטרמיננטה שלה עדיין תהיה שווה לאפס, וזה עבור כל שורה ועמודה שנמחק, כלומר \(\text{adj}L_{G}=0\) . מכיוון שבאופן כללי, \(\left|L_{G}^{11}\right|=\kappa\) אז במקרה שלנו המסקנה היא ש-\(\kappa=0\) ולכן באמת מתקיים \(\text{adj}L_{G}=\kappa J\) ; לכן המקרה המעניין של ההוכחה הוא זה שבו \(\text{rank} L_{G}=n-1\) (זה המקרה שבו \(G\) הוא גרף מעניין שבאמת יש בו עצים פורשים).

בשביל המקרה הזה, לב העניין הוא הנוסחה \(A\cdot\text{adj}A=\left|A\right|\cdot I\)
שהראיתי קודם. במקרה שלנו התחלנו מזה של-\(L_{G}\) יש ערך עצמי 0, ולכן \(\left|L_{G}\right|=0\) , אז קיבלנו

\(L_{G}\cdot\text{adj}L_{G}=0\)
זה אומר שכל עמודה של \(\text{adj}L_{G}\) שייכת לגרעין של \(L_{G}\) . מה הגרעין הזה? מכיוון ש-\(\text{rank} L_{G}=n-1\) , המימד של הגרעין הוא 1 (זה עוד להטוט אלגברה לינארית סטנדרטית שאני מניח שאנחנו מכירים) ואנחנו כבר ראינו איבר ששייך לגרעין של \(L_{G}\) , בהתחלה: הוקטור שכולו 1-ים. המסקנה היא שכל עמודה של \(\text{adj}L_{G}\) היא כפל של הוקטור הזה בסקלר כלשהו ובפרט כל האיברים של העמודה שווים. העניין הוא שבעמודה ה-\(i\)
של \(\text{adj}L_{G}\) יש לנו את \(\left|L_{G}^{ii}\right|\)
שאנחנו יודעים בזכות קירקהוף ששווה ל-\(\kappa\) , ולכן כל האיברים בעמודה הזו שווים ל-\(\kappa\) , ולכן כל המטריצה שווה ל-\(\kappa\) וקיבלנו \(\text{adj}L_{G}=\kappa J\) בדיוק כפי שרצינו.

אוקיי, זה היה די מגניב (ולא ידעתי את זה לפני שהתחלתי לכתוב את הפוסט - כלומר, את העניין הזה שלא חייבים להסיר שורה ועמודה שמתאימות לאותו \(i\) אלא אפשר להסיר \(i,j\) כלליות ומקסימום לכפול במינוס 1). אבל איך זה עוזר לי?

ובכן, הנה תוצאה מרהיבה (שלהבנתי מופיעה לראשונה במאמר עם השם הבלתי קשור בעליל, "On the mutual cancellation of cluster integrals in Mayer's fugacity series," של H. Temperley) שמאפשרת לנו לקבל את \(\kappa\) מתוך \(L_{G}\) בלי בכלל כל העניין השרירותי הזה של לבחור \(i\) ולמחוק מ-\(L_{G}\)
את השורה והעמודה ה-\(i\) :

\(\kappa=\frac{\left|L_{G}+J\right|}{n^{2}}\)
כלומר, במקום למחוק אפשר לחבר 1 לכל כניסה של \(L_{G}\) , לחשב דטרמיננטה, ובסוף לחלק ב-\(n^{2}\) . לא רק שזו תוצאה יפהפייה בזכות עצמה, עוד רגע נראה שהיא גם נותנת לנו את \(\kappa=\frac{1}{n}\lambda_{1}\cdots\lambda_{n-1}\)
בלי כמעט מאמץ. אבל קודם כל בואו נוכיח אותה.

ההוכחה היא מאוד אלגברית - כלומר, כופלים ומחברים דברים והופס, פתאום מקבלים את הנוסחה משום מקום. בשביל זה קודם כל נשים לב לכך ש-\(J^{2}=nJ\) (פשוט על פי ההגדרה הרגילה של כפל מטריצות וזה ש-\(J\) היא מסדר \(n\times n\) ) ו-\(JL_{G}=0\) (כי כפי שכבר ראינו \(L_{G}J=0\) ושתי המטריצות הללו סימטריות) ועכשיו נחשב אלגברית את

\(\left(nI-J\right)\left(J+L_{G}\right)=nJ-J^{2}+nL_{G}-JL_{G}=nL_{G}\)
עכשיו, באופן כללי אם יש לנו את המכפלה \(AB\) אז אפשר להראות ש-\(\text{adj}\left(AB\right)=\text{adj}B\cdot\text{adj}A\) . זו תכונה סטנדרטית ולכן לא אוכיח אותה כאן, אבל תראו מה היא נותנת לנו:

\(\text{adj}\left(J+L_{G}\right)\text{adj}\left(nI-J\right)=\text{adj}\left(nL_{G}\right)\)
עכשיו, \(nI-J\) זו מטריצה מעניינת. יש לה \(n-1\) על האלכסון הראשי, ו-\(-1\) בכל מקום אחד - זה הלפליסאן של הגרף המלא על \(n\) צמתים. מספר העצים הפורשים של הגרף המלא על \(n\) צמתים הוא פשוט מספר העצים על \(n\) צמתים - זו תוצאה סטנדרטית שנקראת נוסחת קיילי וכשכתבתי את הפוסט הזה גיליתי למרבה הזוועה שעוד אין לי פוסט עליה - אז עכשיו כבר יש. ההוכחה של הנוסחה הזו מרהיבה, אבל היא עצמה מאוד פשוטה: יש \(n^{n-2}\) עצים כאלו. לכן \(\text{adj}\left(nI-J\right)=n^{n-2}J\) .

עוד איבר שמופיע בנוסחה הוא \(\text{adj}\left(nL_{G}\right)\) . מה אני יכול להגיד עליו? האם אפשר להוציא את הסקלר \(n\) החוצה מה-adj? ובכן, כן. באופן כללי אפשר להוציא סקלרים החוצה מדטרמיננטות: \(\left|\lambda A\right|=\lambda^{n}\left|A\right|\) , כי מה שקורה פה הוא שהכלל עבור דטרמיננטות הוא שלכפול שורה בסקלר \(\lambda\) מכפיל את כל הדטרמיננטה ב-\(\lambda\) . לכן אם הכפלנו את כל המטריצה ב-\(\lambda\) , ויש למטריצה \(n\) שורות, האפקט יהיה להכפיל את הדטרמיננטה \(n\) פעמים ב-\(\lambda\) .

כשלוקחים adj של מטריצה \(A\) מסדר \(n\) , כל כניסה היא עצמה דטרמיננטה: \(\left[\text{adj}A\right]_{ji}=\left(-1\right)^{i+j}\left|A^{ij}\right|\) , אבל זו לא הדטרמיננטה של \(A\) אלא של המינור\(A^{ij}\) שהתקבל מ-\(A\) על ידי מחיקת שורה ועמודה, כלומר זו מטריצה עם \(n-1\)
שורות. לכן \(\left[\text{adj}\lambda A\right]_{ji}=\left(-1\right)^{i+j}\left|\lambda A^{ij}\right|=\lambda^{n-1}\left(-1\right)^{i+j}\left|A^{ij}\right|\) . זה מוביל לכך שבמקרה שלנו:

\(\text{adj}\left(nL_{G}\right)=n^{n-1}\text{adj}\left(L_{G}\right)\)
וכזכור, ראינו גם

\(\text{adj}L_{G}=\kappa J\)
אז בסך הכל \(\text{adj}\left(nL_{G}\right)=n^{n-1}\kappa J\)
אז בואו ניקח את הנוסחה \(\text{adj}\left(J+L_{G}\right)\text{adj}\left(nI-J\right)=\text{adj}\left(nL_{G}\right)\)
שקיבלנו ונכתוב אותה מחדש עם מה שלמדנו:

\(\text{adj}\left(J+L_{G}\right)n^{n-2}J=n^{n-1}\kappa J\)
כלומר

\(\text{adj}\left(J+L_{G}\right)J=n\kappa J\)
איך נתקדם מפה? ובכן, זכרו את הנוסחה שמעניקה ל-adj את הכוח שלה: \(A\cdot\text{adj}A=\left|A\right|\cdot I\) . בואו נשתמש בה פה - ניקח את \(\text{adj}\left(J+L_{G}\right)J=n\kappa J\) ונכפול את שני האגפים במטריצה \(J+L_{G}\) . נקבל:

\(\left(J+L_{G}\right)\text{adj}\left(J+L_{G}\right)J=\left(J+L_{G}\right)n\kappa J\)
נשתמש בנוסחה על אגף שמאל ונקבל

\(\left|\left(J+L_{G}\right)\right|J=\left(J+L_{G}\right)n\kappa J\)
באגף ימין, בואו ניזכר שראינו \(J^{2}=nJ\) ו-\(L_{G}J=0\) ולכן אפשר לפתוח את הסוגריים שם, ולקבל

\(\left|\left(J+L_{G}\right)\right|J=n^{2}\kappa J\)
קיבלנו שאותה מטריצה, מוכפלת בשני סקלרים, היא שווה - אז הסקלרים בהכרח שווים (כי אנחנו עובדים מעל שדה ממציין 0, אם רוצים להיות פדנטיים), כלומר

\(\left|\left(J+L_{G}\right)\right|=n^{2}\kappa\)
או בסימון המקורי שלי:

\(\kappa=\frac{\left|L_{G}+J\right|}{n^{2}}\)
זה מסיים את ההוכחה של התוצאה המאוד יפה הזו, אבל איך זה עוזר לנו עם התמונה הגדולה? כזכור, המטרה שלי היא להראות שעבור מטריצת הלפלסיאן, הדטרמיננטה של כל מינור שלה היא מכפלת הערכים העצמיים ששונה מאפס חלקי \(n\) :

\(\kappa=\frac{1}{n}\lambda_{1}\cdots\lambda_{n-1}\) .

אז מספיק להראות ש-\(\left|L_{G}+J\right|=n\cdot\lambda_{1}\cdots\lambda_{n-1}\)
מה שצריך לזכור הוא שדטרמיננטה של מטריצה הוא מכפלת כל הערכים העצמיים שלה, כמו שהראיתי קודם. ומה הערכים העצמיים של \(L_{G}+J\) ? או, כאן זה נהיה כיף. ראינו כזכור ש-\(L_{G}J=JL_{G}=0\) , כלומר המטריצות הללו מתחלפות בכפל.

מטריצות לכסינות שמתחלפות בכפל הן לכסינות סימולטנית, כלומר אותה מטריצה\(P\) מלכסנת את שתיהן ביחד. אם \(A,B\) שתיהן לכסינות ומקיימות \(AB=BA\) זה אומר שקיימת מטריצה אחת, \(P\) כך ש-\(P^{-1}AP=D_{A}\) ו-\(P^{-1}BP=D_{B}\) , והערכים שמופיעים באלכסונים של המטריצות האלכסוניות \(D_{A},D_{B}\) הם הערכים העצמיים של \(A,B\) בהתאמה. שימו לב שהערכים הללו לא מופיעים בסדר שרירותי; הערך העצמי ה-\(k\) -י באלכסון הוא הערך העצמי שמתאים לוקטור העצמי ה-\(k\) -י ב-\(P\) (העמודות של \(P\) כולן וקטורים עצמיים של \(A,B\) ; הרעיון בלכסון סימולטני הוא שיש לנו את אותם וקטורים עצמיים לשתי המטריצות בו זמנית).

עכשיו, \(P^{-1}\left(A+B\right)P=D_{A}+D_{B}\) , ולכן הערכים העצמיים של \(A+B\) הם בדיוק אברי האלכסון של \(D_{A}+D_{B}\) , כלומר, הערכים העצמיים הללו הם מה שמתקבל כשמחלקים את הערכים העצמיים של \(A,B\)
לזוגות, בהתאם לוקטורים העצמיים שלהם, וסוכמים כל זוג.

את כל זה אפשר לעשות גם במקרה שבו המטריצות לא לכסינות אלא רק ניתנות לשילוש בעזרת צורת ז'ורדן. במקרה הספציפי שלנו, אנחנו יודעים על וקטורים עצמי משותף אחד: הוקטור שכולו 1-ים, שמתאים לערך העצמי \(0\) של \(L_{G}\) ולערך העצמי \(n\) של \(J\) , ולכן הערך העצמי של \(L_{G}+J\) שמתאים אליו יהיה \(n\) . כל שאר הערכים העצמיים של \(J\) הם 0 (כי זו מטריצה מדרגה 1) ולכן כל יתר הערכים העצמיים של \(L_{G}+J\) יהיו פשוט הערכים העצמיים \(\lambda_{1},\ldots,\lambda_{n-1}\) כשמחברים 0 לכל אחד מהם. קיבלנו שהערכים העצמיים של \(L_{G}+J\) הם בדיוק \(n,\lambda_{1},\ldots,\lambda_{n-1}\) ולכן \(\left|L_{G}+J\right|=n\cdot\lambda_{1}\cdots\lambda_{n-1}\) וזה מסיים את ההוכחה.

יפה! סיימנו את... השלב הראשון בכל הסיפור הזה. נותרו לנו עוד שניים: הקטע הזה של גרף מכפלה, והקטע הזה של פולינומי צ'בישב.

הקטע הזה של גרף מכפלה

באופן כללי מתמטיקה זה מסובך ואובייקטים מתמטיים זה מסובך, אז המתמטיקאים מנסים בכל הזדמנות לקחת אובייקט מסובך ולהציג אותו בתור משהו שנבנה מאובייקטים פשוטים יותר, שקל לנו להבין יותר אותם ואת מה שקורה בעקבות הפעולות שביצענו עליהם כדי לקבל את הדבר המסובך. ככה זה עם הצגה של מספר טבעי בתור מכפלה של ראשוניים; של חבורה בתור מכפלה של תת-חבורות; של מרחב וקטורי בתור מכפלה של מרחבים וקטוריים; של... טוב, הבנתם, אני אוהב מכפלות. למה שלא יהיה משהו כזה גם לגרפים?

ובכן, לא רק שיש, יש הרבה. אני אדבר רק על ההגדרה הספציפית של מכפלה שאני צריך בפוסט הזה - לפעמים קוראים לה "מכפלה קרטזית" ולפעמים "מכפלת קופסה" . הרעיון הוא כזה: אם יש לנו שני גרפים, \(G_{1}=\left(V_{1},E_{1}\right)\) ו-\(G_{2}=\left(V_{2},E_{2}\right)\)
אז נבנה גרף חדש, \(G_{1}\square G_{2}=\left(V,E\right)\) כך ש-

\(V=V_{1}\times V_{2}=\left\{ \left(v_{1},v_{2}\right)\ |\ v_{1}\in V_{1},v_{2}\in V_{2}\right\}\)
כלומר, הצמתים של הגרף החדש הם זוגות של צומת מכל אחד מהגרפים המקוריים - הקבוצה הזו היא בדיוק מה שנקרא "מכפלה קרטזית" של הקבוצות \(V_{1},V_{2}\) ומכאן השם של המכפלה הזו גם כאן. אבל עוד לא סיימנו - גרף מוגדר לא רק על ידי הצמתים שלו אלא על ידי הקשתות, ובמקרה הזה לא יתקיים ש-\(E=E_{1}\times E_{2}\) (למעשה, אין ממש משמעות להגדרה כזו - המכפלה של \(E_{1},E_{2}\) לא נותנת לנו קבוצה של קשתות על צמתי \(V\) ). ההגדרה, שתתאים בול למבוכים שאני ממדל בעזרת הגרפים הללו ואולי יהיה קל להבין אותה יותר באמצעותם, היא ששני צמתים מחוברים בקשת אם בקואורדינטה אחת שלהם הם זהים ובקואורדינטה השניה שלהם הם מחוברים בקשת. פורמלית (ואני לא בטוח שהכתיב הפורמלי עוזר לזה להיות ברור):

\(E=\left\{ \left(\left(v_{1},v_{2}\right),\left(u_{1},v_{2}\right)\right)\ |\ \left(v_{1},u_{1}\right)\in E_{1}\right\} \cup\left\{ \left(\left(v_{1},v_{2}\right),\left(v_{1},u_{2}\right)\right)\ |\ \left(v_{2},u_{2}\right)\in E_{2}\right\}\)
הנה דרך אינטואיטיבית לחשוב על זה. נניח שלבי במזרח ואנוכי בסוף מערב ויש לי כוחות על שמאפשרים לי להתפצל תודעתית: חלק אחד שלי יצא לטיול בירושלים וחלק אחר מטייל בקורדובה בספרד. בשני המקרים הרחובות ארוכים וצרים ומתפתלים - אפשר למדל אותם עם גרף. צמתים הם מקומות שבהם אפשר לעצור ולהתפעל מהנוף, וקשתות הן הסמטאות שמחברות שני מקומות כאלו. אז יש לנו גרף \(G_{1}\) עבור ירושלים וגרף \(G_{2}\) עבור קורדובה. בדרך כלל כשאני מטייל אני נמצא רק במיקום גאוגרפי אחד, נאמר בירושלים, ואז הטיול שלי הוא סדרה של מעברים מצומת \(v\in V_{1}\) אל צומת \(u\in V_{1}\) בעזרת הקשת \(\left(v,u\right)\in E_{1}\) . אבל עכשיו, כאמור, אני באורח פלא גם פה וגם שם: המיקום שלי הוא \(\left(v_{1},v_{2}\right)\)
כש-\(v_{1}\) הוא המיקום שלי בירושלים ו-\(v_{2}\) הוא המיקום שלי בקורדובה.

עכשיו, יש עלי רק מגבלה אחת למרות כוח העל המדהים שלי: כשאני זז, אני לא מסוגל לזוז גם פה וגם שם בו זמנית, הסמטאות המפותלות דורשות יותר מדי ריכוז. אז אם אני רוצה לזוז ממקום \(v_{1}\) למקום \(u_{1}\)
בירושלים אני "מקפיא" לרגע את מה שאני עושה בקורדובה - הייתי ב-\(v_{2}\) ואשאר לעת עתה ב-\(v_{2}\) . אז המעבר שלי הוא מהצומת \(\left(v_{1},v_{2}\right)\) אל הצומת \(\left(u_{1},v_{2}\right)\) - זזתי בקואורדינטה הראשונה, והשניה נשארה ללא שינוי. באותו אופן גם הייתי יכול לזוז בקורדובה ולהישאר בירושלים.

כל זה עובד מצוין עבור המבוכים שלנו. אצלנו, הגרף שאנחנו רוצים לספור לו עצים פורשים הוא מהצורה \(G=\left(V,E\right)\) עם \(V=\left\{ \left(i,j\right)\ |\ 1\le i\le n,1\le j\le m\right\}\) (כאשר \(\left(i,j\right)\) אומר "התא בשורה ה-\(i\) בעמודה ה-\(j\) "). הקשתות הן מהצורה \(\left(\left(i,j\right),\left(i+1,j\right)\right)\) (כשזזים משורה אחת לאחרת, כלומר נעים בקו אנכי) ו-\(\left(\left(i,j\right),\left(i,j+1\right)\right)\) (כשזזים מעמודה אחת לאחרת, כלומר נעים בקו אופקי). אי אפשר במבוך לזוז "באלכסון" כמו שהיה קורה אם היה מותר לזוז ב-\(G_{1},G_{2}\) "בו זמנית" . אז אפשר לחשוב על \(G\) בתור המכפלה \(G_{1}\square G_{2}\) כאשר כל אחד מהמוכפלים הוא פשוט מאוד: \(G_{1}=\left(V_{1},E_{1}\right)\) כך ש-\(V_{1}=\left\{ 1,2,\ldots,n\right\}\) ו-\(E_{1}\) כוללת את כל האיברים מהצורה \(\left(i,i+1\right)\) עבור \(1\le i\lt n\) , ו-\(G_{2}\) מוגדר באותו אופן עם \(m\) במקום \(n\) . מכיוון שאני עצלן ביקשתי מבינה מלאכותית לאייר לי את זה והתוצאה הזויה בהתאם אבל מדויקת למדי:

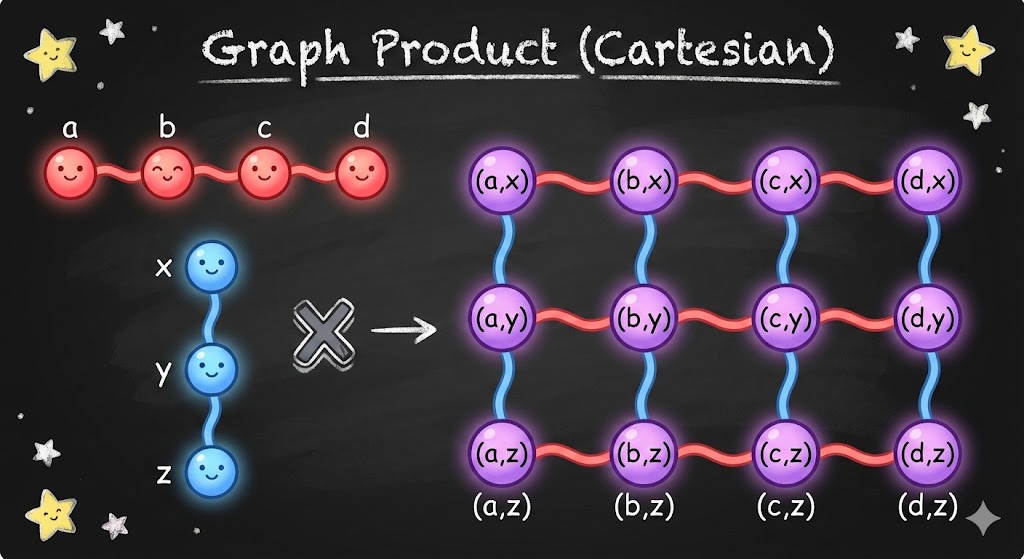
מה שאני מתעניין בו בפוסט הזה הוא הלפלסיאן של גרפים, וספציפית הערכים העצמיים שלו כי כבר עברנו מהבעיה של חישוב הדטרמיננטה של הלפלסיאן לבעיה של מציאת הערכים העצמיים שלו. אז מה אני יכול לומר על הערכים העצמיים של \(L_{G_{1}\square G_{2}}\) ? או, בשביל זה אני יכול להיעזר במה שאנחנו יודעים על תורת המטריצות, בתנאי שאני אבין איך לכתוב את \(L_{G_{1}\square G_{2}}\) בעזרת \(L_{G_{1}},L_{G_{2}}\) וזה, למרבה המזל, די קל: \(L_{G_{1}\square G_{2}}\) הולך לצאת מה שנקרא סכום קרונקר של \(L_{G_{1}},L_{G_{2}}\) , וזו הזדמנות טובה להציג את המושג הזה.

באופן כללי, אם \(A,B\) הן שתי מטריצות ריבועיות מסדר \(n\times n\)
ו-\(m\times m\) בהתאמה, אז מכפלת קרונקר שלהן, שמסומנת \(A\otimes B\) , היא מה שמקבלים אם לוקחים את \(A\) ובכל כניסה של \(A\) שותלים עותק שלם של \(B\) בתור בלוק, כשכל העותק הזה מוכפל במה שהיה בכניסה של \(A\) במקור. הנה דוגמא פשוטה:

\(A=\left(\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right),B=\left(\begin{array}{cc} b_{11} & b_{12}\\ b_{21} & b_{22} \end{array}\right)\)
וכעת:

\(A\otimes B=\left(\begin{array}{cc} a_{11}B & a_{12}B\\ a_{21}B & a_{22}B \end{array}\right)\)
שימו לב, אני לא אומר ש-\(a_{11}B\) הוא איבר של המטריצה החדשה; אני אומר שזה תיאור של המטריצה החדשה בתור מטריצת בלוקים. כלומר, פורמלית קיבלנו את המטריצה

\(A\otimes B=\left(\begin{array}{cccc} a_{11}b_{11} & a_{11}b_{12} & a_{12}b_{11} & a_{12}b_{12}\\ a_{11}b_{21} & a_{11}b_{22} & a_{12}b_{21} & a_{12}b_{22}\\ a_{21}b_{11} & a_{21}b_{12} & a_{22}b_{11} & a_{22}b_{12}\\ a_{21}b_{21} & a_{21}b_{22} & a_{22}b_{21} & a_{22}b_{22} \end{array}\right)\)
מקום אחד שבו המפלצת הזו צצה באופן טבעי והיא שימושית מאוד הוא חישוב קוונטי, ויש לי פוסט שבו אני מתאר אותה בהקשר הזה. אבל מן הסתם יש לה שלל שימושים שונים ומשונים - זה עתה נתקלנו באחד חדש. רק שצריך טיפה להיזהר - אני הגדרתי כרגע את מכפלת קרונקר, אבל עבור \(L_{G_{1}\square G_{2}}\) אני צריך משהו שנקרא סכום קרונקר שהוא מושג קשור שמתבסס על המכפלה אבל לא זהה.

בואו נגדיר סכום קרונקר בצורה זהירה. יש לנו כאמור מטריצה ריבועית \(A\) מסדר \(n\) ומטריצה ריבועית \(B\) מסדר \(m\) . מכפלת קרונקר שלהם תהיה מטריצה ריבועית מסדר \(nm\) . גם סכום קרונקר יהיה מהסדר הזה, אבל הוא מתקבל בצורה שונה: ניקח את מטריצת היחידה מסדר \(m\) ונסמן אותה \(I_{m}\) ובדומה נסמן ב-\(I_{n}\) את מטריצת היחידה מסדר \(n\) , ועכשיו נסתכל על הביטוי הזה:

\(A\oplus B\triangleq A\otimes I_{m}+I_{n}\otimes B\)
כלומר, במקום לכפול את \(A,B\) ישירות זה עם זה, אנחנו כופלים אותם עם מטריצות היחידה מהסדרים המתאימים, מקבלים שתי מטריצות מסדר \(nm\) ומחברים אותן. אם נעשה את זה עבור שתי המטריצות מסדר \(2\times2\) שהראיתי קודם, נקבל

\(A\oplus B=A\otimes I_{2}+I_{2}\otimes B=\left(\begin{array}{cc} a_{11}I_{2} & a_{12}I_{2}\\ a_{21}I_{2} & a_{22}I_{2} \end{array}\right)+\left(\begin{array}{cc} B & 0\\ 0 & B \end{array}\right)=\)

\(=\left(\begin{array}{cccc} a_{11}+b_{11} & b_{12} & a_{12} & 0\\ b_{21} & a_{11}+b_{22} & 0 & a_{12}\\ a_{21} & 0 & a_{22}+b_{11} & b_{12}\\ 0 & a_{21} & b_{21} & a_{22}+b_{22} \end{array}\right)\)
כדי להבין מה הקטע, כדאי לזכור מה בעצם מכפלת קרונקר של מטריצות באה להשיג. אני לא מציג בפוסט הזה את המושג של מכפלה טנזורית של מרחבים וקטוריים אבל הזכרתי את זה בפוסט של החישוב הקוונטי (שם מכפלות טנזוריות צצות באופן טבעי - אפשר לחשוב על קיוביט בתור מרחב וקטורי ממימד 2, ועל אוסף של \(n\) קיוביטים בתור מכפלה טנזורית של \(n\) מרחבים שכאלו) וגם יש לי פוסט ייעודי על הקונספט. עכשיו, בואו נגיד שיש לנו מכפלה טנזורית של שני מרחבים וקטוריים \(V\otimes U\) ואיבר במכפלה הזו שהוא מהצורה \(v\otimes u\) (לא כל איבר של \(V\otimes U\) נראה ככה, אבל איברים מהצורה הזו פורשים את המרחב וזה מספיק טוב לנו). עכשיו, נניח שיש לנו טרנספורמציה לינארית על \(V\) שמיוצגת על ידי \(A\) וטרנספורמציה לינארית על \(U\) שמיוצגת על ידי \(B\) , אז מכפלת קרונקר שלהם משיגה את האפקט הבא:

\(\left(A\otimes B\right)\left(v\otimes u\right)=\left(Av\right)\otimes\left(Bu\right)\)
בלשון של חישוב קוונטי, אם יש לנו שני שערים \(A,B\) שפועלים כל אחד על קיוביט בודד, אז \(A\otimes B\) יהיה השער שפועל על שני קיוביטים: על השער הראשון כמו \(A\) ועל השער השני כמו \(B\) .

עכשיו, שימו לב שאם \(v\) הוא וקטור עצמי של \(A\) עם הערך העצמי \(\lambda\) , כלומר \(Av=\lambda v\) , ואם \(u\) הוא וקטור עצמי של \(B\) עם הערך העצמי \(\rho\) , כלומר \(Bu=\rho u\) , אז יתקיים

\(\left(A\otimes B\right)\left(v\otimes u\right)=\left(Av\right)\otimes\left(Bu\right)=\left(\lambda v\right)\otimes\left(\rho u\right)=\lambda\rho\left(v\otimes u\right)\) (המעבר האחרון משתמש בכללים של מכפלה טנזורית שלא הצגתי כאן במפורש)

כלומר, \(\lambda\rho\) הוא ערך עצמי של \(A\otimes B\) , וזה מה שקורה באופן כללי: הערכים העצמיים של \(A\otimes B\) הם המכפלות של כל הזוגות האפשריים של ערך עצמי של \(A\) וערך עצמי של \(B\) . זה מה שקורה עבור מכפלת קרונקר. ועבור סכום? כפי שאפשר לנחש, נקבל סכום של הערכים העצמיים:

\(\left(A\otimes I_{m}+I_{n}\otimes B\right)\left(v\otimes u\right)=\left(A\otimes I_{m}\right)\left(v\otimes u\right)+\left(I_{n}\otimes B\right)\left(v\otimes u\right)=\)

\(\left(Av\otimes Iu\right)+\left(Iv\otimes Bu\right)=\left(\lambda v\otimes u\right)+\left(v\otimes\rho u\right)=\lambda\left(v\otimes u\right)+\rho\left(v\otimes u\right)=\)

\(\left(\lambda+\rho\right)\left(v\otimes u\right)\) (שוב, כל זה בעזרת הכללים הסטנדרטיים של מכפלה טנזורית).

יפה, אז אפשר לחזור לגרפים. אם אני אראה שהלפלסיאן \(L_{G_{1}\square G_{2}}\) של גרף המכפלה הוא סכום קרונקר של הלפלסיאנים \(L_{G_{1}},L_{G_{2}}\) אני אקבל מייד שהערכים העצמיים שלו הם סכומים של זוגות של הערכים העצמיים שלהם - בדיוק מה שרציתי.

במבט ראשון, זה נראה ממש מעייף להתחיל להוכיח את זה - \(A\oplus B\) היא מטריצה מעיקה כבר בדוגמא הקטנה שנתתי למעלה, אז לטפל בה באופן כללי יהיה סיוט של טיפול באינדקסים. הסיוט הזה די נעלם אם חושבים על \(A\oplus B\) בתור מטריצה שהאינדקסים שלה הם לא מספרים אלא זוגות של מספרים. כלומר, נמספר את השורות והעמודות על ידי זוגות \(\left(i,j\right)\) כך ש-\(1\le i\le n\) ו-\(1\le j\le m\) , ואז כניסה כללית של המטריצה תהיה מהצורה \(\left(i,j\right),\left(i^{\prime},j^{\prime}\right)\) . הסדר שבו אנחנו מסדרים בו את האיברים הללו הוא לקסיקוגרפי - קודם כל מגדילים את הכניסה השניה ואז, כשהיא הגיעה לערך המקסימלי שלה, מחזירים אותה לערך המינימלי ומגדילים את הכניסה הראשונה. כלומר הסדר הוא \(\left(1,1\right),\left(1,2\right),\left(2,1\right),\left(2,2\right)\) .

עכשיו, אם מסתכלים על הדוגמא למעלה עם האינדקסים מול העיניים

\(\begin{array}{c} \begin{array}{c} \\\left(1,1\right)\\ \left(1,2\right)\\ \left(2,1\right)\\ \left(2,2\right) \end{array}\begin{array}{cccc} \left(1,1\right) & \left(1,2\right) & \left(2,1\right) & \left(2,2\right)\\ a_{11}+b_{11} & b_{12} & a_{12} & 0\\ b_{21} & a_{11}+b_{22} & 0 & a_{12}\\ a_{21} & 0 & a_{22}+b_{11} & b_{12}\\ 0 & a_{21} & b_{21} & a_{22}+b_{22} \end{array}\end{array}\)
רואים שהכללים של מהי \(A\otimes I_{2}+I_{2}\otimes B\) הם די פשוטים: 1. על האלכסון יש לנו במקום \(\left(i,j\right),\left(i,j\right)\) את \(a_{ii}+b_{jj}\) .

1. בשורה \(\left(i,j\right)\) ובעמודה \(\left(i,j^{\prime}\right)\) עבור \(j\ne j^{\prime}\) יש לנו את \(b_{j,j^{\prime}}\) .

2. בשורה \(\left(i,j\right)\) ובעמודה \(\left(i^{\prime},j\right)\)
   עבור \(i\ne i^{\prime}\) יש לנו את \(a_{i,i^{\prime}}\)

3. בכל מקום אחר יש לנו 0.

כמובן, זה אפילו יותר פשוט מזה: הכלל הכללי ביותר הוא שהכניסה בשורה \(\left(i,j\right)\) ועמודה \(\left(i^{\prime},j^{\prime}\right)\)
מקבלת את המחובר \(a_{i,i^{\prime}}\) אם \(j=j^{\prime}\) ואת המחובר \(b_{j,j^{\prime}}\) אם \(i=i^{\prime}\) .

קל במיוחד לראות את זה עבור \(I_{2}\otimes B\) , כלומר המטריצה שנראית כמו \(\left(\begin{array}{cccc} B & 0 & 0 & 0\\ 0 & B & 0 & 0\\ 0 & 0 & \ddots & 0\\ 0 & 0 & 0 & B \end{array}\right)\) . כל בלוק של \(B\) מתאים לאינדקסים מהצורה \(\left(1,j\right),\left(2,j\right),\ldots,\left(n,j\right)\) עבור \(1\le j\le m\) כלשהו. (האינדקסים הללו מתאימים לשורת/עמודות רצופות בגלל הסדר הלקסיקוגרפי). אז בהינתן כניסה כלשהי בשורה \(\left(i,j\right)\) , הסיכוי היחידי שלה להיות שונה מאפס ב-\(I_{2}\otimes B\) הוא שהעמודה תהיה באותו בלוק כמו השורה - כלומר העמודה צריכה להיות \(\left(i^{\prime},j\right)\) (אותו ה-\(j\) ).

עכשיו נחזור אל הלפלסיאנים. בלפלסיאן של גרף, כל כניסה מייצגת צומת. כשהגרף הוא מכפלה \(G_{1}\square G_{2}\) , כל צומת הוא זוג \(\left(i,j\right)\)
כך ש-\(i\) שייך לאינדקסים של צמתי \(G_{1}\) ו-\(j\) שייך לאינדקסים של צמתי \(G_{2}\) - כבר טוב, כי ראינו שבסכום קרונקר גם כן נוח לנו לאנדקס דברים עם זוגות כאלו. עבור אברי האלכסון, כלומר זוגות מהצורה \(\left(i,j\right),\left(i,j\right)\) , אמורה להיות לנו הדרגה של הצומת \(\left(i,j\right)\) ובפועל כפי שראינו למעלה מה שיש לנו הוא את \(a_{ii}+b_{jj}\) , כלומר את האיברים על האלכסון שמתאימים ל-\(i\) ב-\(G_{1}\) ול-\(j\) ב-\(G_{2}\) - כלומר את סכום הדרגות של הצמתים הללו בגרפים המקוריים שלהם. האם זה מה שצריך להיות? כן! כי מי השכנים של הצומת \(\left(i,j\right)\)
בגרף המכפלה? כל הצמתים מהצורה \(\left(i,j^{\prime}\right)\) כך ש-\(j^{\prime}\) היה שכן של \(j\) ב-\(G_{2}\) , וכל הצמתים מהצורה \(\left(i^{\prime},j\right)\) כך ש-\(i^{\prime}\) היה שכן של \(i\) ב-\(G_{2}\) . כלומר בדיוק סכום השכנים של שני הצמתים הללו בגרפים המקוריים.

עבור כניסה \(\left(i,j\right),\left(i^{\prime},j^{\prime}\right)\)
שלא על האלכסון, הלפלסיאן אמור לתת לנו את מינוס מספר הקשתות מהצומת \(\left(i,j\right)\) לצומת \(\left(i^{\prime},j^{\prime}\right)\) . אם גם \(i\ne i^{\prime}\) וגם \(j\ne j^{\prime}\) אז כפי שראינו המספר הזה הוא 0, וזה מה שהוא צריך להיות כי על פי הגדרת גרף מכפלה, אין קשת בין הצמתים הללו - יש קשת רק בין צמתים שנבדלים בדיוק ברכיב אחד. אז מה קורה אם למשל \(i=i^{\prime}\) אבל \(j\ne j^{\prime}\) ? במקרה הזה, הכניסה \(\left(i,j\right),\left(i,j^{\prime}\right)\) היא \(b_{j,j^{\prime}}\) , כלומר הכניסה המתאימה בלפלסיאן של \(G_{2}\)
- והכניסה הזו נותנת את מספר הקשתות מ-\(j\) אל \(j^{\prime}\) , שהוא גם בדיוק מספר הקשתות מ-\(\left(i,j\right)\) אל \(\left(i,j^{\prime}\right)\) . אז הכל מסתדר יפה.

נסכם: אם יש לנו גרף מכפלה \(G_{1}\square G_{2}\) , הלפלסיאן שלו אכן יוצא סכום קרונקר של הלפלסיאנים המעורבים, מה שאפשר לכתוב בנוסחה קומפקטית בתור

\(L_{G_{1}\square G_{2}}=L_{G_{1}}\oplus L_{G_{2}}\)
ואנחנו יודעים בדיוק מה הערכים העצמיים של סכום קרונקר - כל הסכומים של זוגות של ערכים עצמיים של המטריצות שאותן סוכמים.

עכשיו רק נשאר ליישם את זה למקרה הקונקרטי שלנו - גרף מכפלה שבנוי משני גרפים שהם "שרוך" ואפשר למצוא את הערכים העצמיים שלהם במפורש עם הקטע הזה של פולינומי צ'בישב.

הקטע הזה של פולינומי צ'בישב

לפני שאני מתחיל לשלוף את צ'בישב, בואו נבין מה בכלל אנחנו רוצים לעשות ולמה זה לא לגמרי טריוויאלי. הצלחנו לרדקץ את כל המהומה של המבוכים אל ההבנה של גרף אחד ספציפי: \(P_{n}=\left(V,E\right)\) כך ש-\(V=\left\{ 1,2,\ldots,n\right\}\) ו-\(E=\left\{ \left(1,2\right),\left(2,3\right),\ldots,\left(n-1,n\right)\right\}\) . גרף שנראה כמו קו אחד ארוך - או בקיצור, "שרוך" . בואו נכתוב במפורש את הלפלסיאן של גרף כזה עם חמישה צמתים:

\(\left(\begin{array}{ccccc} 1 & -1 & 0 & 0 & 0\\ -1 & 2 & -1 & 0 & 0\\ 0 & -1 & 2 & -1 & 0\\ 0 & 0 & -1 & 2 & -1\\ 0 & 0 & 0 & -1 & 1 \end{array}\right)\)
זו מטריצה פשוטה מאוד, בצורה כמעט מרגיזה: שני האלכסונים המשניים שלה הם כולם \(-1\) , האלכסון הראשי שלה הוא כמעט כולו 2 למעט שני הצדדים שהם 1. אולי אפשר לחשב את הפולינום האופייני שלה פשוט על ידי ההגדרה, באמצעות חישוב דטרמיננטה? אנחנו צריכים לחשב את הדטרמיננטה הבאה:

\(\left|\begin{array}{ccccc} x-1 & 1 & 0 & 0 & 0\\ 1 & x-2 & 1 & 0 & 0\\ 0 & 1 & x-2 & 1 & 0\\ 0 & 0 & 1 & x-2 & 1\\ 0 & 0 & 0 & 1 & x-1 \end{array}\right|\)
אפשר להתחיל לחשב אותה על ידי פיתוח של השורה העליונה. זה אומר שלוקחים את \(x-1\) ומכיפילים בדטרמיננטה שמתקבלת ממחיקת השורה והעמודה הראשונים. אחר כך מפחיתים את ה-1 שבעמודה השניה בשורה הראשונה, כשהוא מוכפל בדטרמיננטית המינור שמתקבל ממחיקת השורה הראשונה והעמודה השניה, כלומר

\(\left|\begin{array}{cccc} 1 & 1 & 0 & 0\\ 0 & x-2 & 1 & 0\\ 0 & 1 & x-2 & 1\\ 0 & 0 & 1 & x-1 \end{array}\right|\)
את הדטרמיננטה הזו קל מאוד לפשט כי בעמודה הראשונה יש 1 רק ותו לא, אז מסירים את העמודה והשורה הראשונים ומקבלים

\(\left|\begin{array}{ccc} x-2 & 1 & 0\\ 1 & x-2 & 1\\ 0 & 1 & x-1 \end{array}\right|\)
וזה מה שמקבלים כשמסירים מהמטריצה המקורית את שתי השורות והעמודות הראשונות. כלומר יש לנו מעין רקורסיה להתבסס עליה כאן - נחשב את הדטרמיננטה של המטריצה המקורית על ידי חישוב של דטרמיננטות של תת-מטריצות שמתקבלות ממנה על ידי מחיקת כך-וכך השורות והעמודות הראשונות. מקרי הבסיס הם כשמחקנו את הכל חוץ מהתא הימני-תחתון \(x-1\) - נסמן זאת בתור \(p_{1}\left(x\right)=x-1\) , והמקרה העוד יותר מנוון כשמחקנו את הכל ולכן יש לנו את "המכפלה הריקה"\(1\) , ואת זה נסמן ב-\(p_{0}\left(x\right)=1\) .

עכשיו, החישוב שעשיתי קודם כלל להסיר שורה ועמודה אחת ולהכפיל ב-\(x-1\) , אבל זה היה למעשה מקרה מיוחד כי היה \(x-1\) בפינה השמאלית-עליונה של המטריצה; בדרך כלל יהיה שם \(x-2\) . אז אני מקבל את הנוסחה הבאה:

\(p_{k}=\left(x-2\right)p_{k-1}\left(x\right)-p_{k-2}\left(x\right)\)
הנוסחה הזו עובדת עד שאנחנו מגיעים לשלב האחרון, ואז צריך יהיה להכפיל ב-\(x-1\) כדי לקבל את \(L_{G}\) . כלומר אנחנו מקבלים את הנוסחה הכללית הזו לחישוב סדרת פולינומים \(p_{k}\) עבור \(1\le k\lt n\) :

\(p_{0}\left(x\right)=1\)

\(p_{1}\left(x\right)=x-1\)

\(p_{k}\left(x\right)=\left(x-2\right)p_{k-1}\left(x\right)-p_{k-2}\left(x\right)\)
עבור \(2\le k\lt n\) .

ואז מגיע השלב האחרון:

\(L_{G}=\left(x-1\right)p_{n-1}\left(x\right)-p_{n-2}\left(x\right)\)
הנוסחה עבור \(p_{k}\) מזכירה בצורה חשודה את הנוסחה של סדרת פולינומים מפורסמת - פולינומי צ'בישב. אלו פולינומים חשובים ומועילים בזכות עצמם - אני בכלל הכרתי אותם לראשונה בהקשר של אנליזה נומרית וקירובים - אבל בפוסט הזה אני לא אכנס לזה. עדיין, כדאי להבין מאיפה הם מגיעים. והם מגיעים מהזוועה שהטרידה אותי בשיעורי המתמטיקה בתיכון - זהויות טריגונומטריות. ספציפית, הזהות של קוסינוס של זווית כפולה:

\(\cos\left(2\theta\right)=2\cos^{2}\theta-1\)
מה שאנחנו רואים כאן הוא שאפשר לבטא את קוסינוס של זווית כפולה בעזרת קוסינוס רגיל כל עוד אנחנו מרשים לכפול אותו בעצמו, ובמקדמים, ולחבר קבועים - זה מה שנקרא פולינום. אבל למה לעצור כאן? אפשר לנסות לטפל גם ב-\(\cos\left(3\theta\right)\) . כאן זווית כפולה לא תעזור לנו אבל אפשר לכתוב \(3\theta=2\theta+\theta\) ולהשתמש בנוסחה הכללית לסכום זוויות, שהיא...

\(\cos\left(\theta+\varphi\right)=\cos\theta\cos\varphi-\sin\theta\sin\varphi\)
וזה... אה... לא טוב בכלל, כי יש לנו פה סינוס, ואני רציתי למצוא משהו שהוא פולינום אך ורק בקוסינוס. אבל רגע, לא להתאייש, אולי יש דרך לבטל את הסינוס כי הרי יש לנו גם נוסחה להפרש זוויות שנראית כמעט אותו דבר:

\(\cos\left(\theta-\varphi\right)=\cos\theta\cos\varphi+\sin\theta\sin\varphi\)
אם אני אחבר את שתי הנוסחאות הללו אני אפטר לגמרי מהסינוס:

\(\cos\left(\theta+\varphi\right)+\cos\left(\theta-\varphi\right)=2\cos\theta\cos\varphi\)
ואם אני אעביר אגף אני אקבל

\(\cos\left(\theta+\varphi\right)=2\cos\theta\cos\varphi-\cos\left(\theta-\varphi\right)\)
יופי. עכשיו אפשר להציב \(\varphi=2\theta\) ולקבל:

\(\cos\left(3\theta\right)=2\cos\theta\cos\left(2\theta\right)-\cos\theta\)
וזו התקדמות! כי את \(\cos\left(2\theta\right)\) אנחנו כבר יודעים לייצג בתור פולינום, אז יש לנו... רקורסיה! בואו נמצא את הנוסחה הכללית של הרקורסיה על ידי חזרה על הטריק של \(\cos\left(\theta+\varphi\right)\) , רק במקום \(\varphi=2\theta\) נציב \(\varphi=n\theta\) עבור \(n\gt 1\) כלשהו, ונקבל

\(\cos\left(\left(n+1\right)\theta\right)=2\cos\theta\cos\left(n\theta\right)-\cos\left(\left(n-1\right)\theta\right)\)
וזה מוכיח לי את התוצאה הבאה: אם אני מגדיר סדרת פולינומים \(T_{n}\left(x\right)\)
על ידי

\(T_{0}\left(x\right)=1\)

\(T_{1}\left(x\right)=x\)

\(T_{n+1}\left(x\right)=2xT_{n}\left(x\right)-T_{n-1}\left(x\right)\)
אז הסדרה תקיים \(\cos\left(n\theta\right)=T_{n}\left(\cos\theta\right)\) . הפולינומים \(T_{n}\) הללו נקראים פולינומי צ'בישב מן הסוג הראשון.

האם זו הסדרה שקיבלנו עם הלפלסיאן שלנו?! אה... לא. הנה מה שקיבלנו:

\(p_{0}\left(x\right)=1\)

\(p_{1}\left(x\right)=x-1\)

\(p_{k}\left(x\right)=\left(x-2\right)p_{k-1}\left(x\right)-p_{k-2}\left(x\right)\)
עבור \(2\le k\lt n\) .

זה דומה אבל זה בוודאי לא זהה. יש כאן בהחלט הליכה של שני צעדים אחורה וחיסור של הפולינום של השני צעדים אחורה, אבל הכפל פה ב-\(x-2\)
ולא ב-\(2x\) . השאלה היא האם זה הבדל מהותי או שאפשר למצוא דרך לבטא את הפולינומים שלנו בעזרת צ'בישב - ובהחלט יש דרך כזו. הנה דרך מסודרת לעשות את זה על ידי ניחוש מושכל.

מה שאני מנחש הוא שעבור \(k\lt n\) מתקיים \(p_{k}\left(x\right)=T_{k}\left(Ax+B\right)\) , כלומר אני לוקח העתקה לינארית("אפינית" למי שרוצים להתקטנן) של הפרמטר של \(T\) ובודק מה משתלם לי שהמקדמים \(A,B\) יצאו. אני יודע שתחת ההנחה הזו מתקיים:

\(T_{k}\left(Ax+B\right)=2\left(Ax+B\right)T_{k-1}\left(Ax+B\right)-T_{k-2}\left(Ax+B\right)=\left(2Ax+2B\right)p_{k-1}\left(x\right)-p_{k-2}\left(x\right)\) ולכן עם השוואה לנוסחת הנסיגה שכבר ראיתי עבור \(p_{k}\left(x\right)\) אני אקבל

\(\left(x-2\right)p_{k-1}\left(x\right)-p_{k-2}\left(x\right)=\left(2Ax+2B\right)p_{k-1}\left(x\right)-p_{k-2}\left(x\right)\)
כלומר, אני צריך שיתקיים \(x-2=2Ax+2B\) , אז יהיה לי הכי פשוט לבחור \(A=\frac{1}{2}\) ו-\(B=-1\) , כלומר לקוות שמתקיים

\(p_{k}\left(x\right)=T_{k}\left(\frac{x-2}{2}\right)\)
לרוע המזל, זה לא קורה. אמנם נוסחת הנסיגה כן עובדת, אבל מה עם תנאי ההתחלה? אמנם \(T_{0}\left(\frac{x-2}{2}\right)=1=p_{0}\left(x\right)\) אבל \(p_{1}\left(x\right)=x-1\) ולעומת זאת \(T_{1}\left(\frac{x-2}{2}\right)=\frac{x-2}{2}\) . החלוקה הזו ב-2 מקלקלת לנו קצת את הסיפור, אבל למרבה המזל אפשר לפתור את זה בקלות על ידי מעבר לפולינומי צ'בישב מן הסוג השני. זו סדרה שמוגדרת כמעט כמו הסוג הראשון, כולל אותה נוסחת נסיגה בדיוק, אבל אחד מתנאי ההתחלה טיפה שונה:

\(U_{0}\left(x\right)=1\)

\(U_{1}\left(x\right)=2x\)

\(U_{n+1}\left(x\right)=2xU_{n}\left(x\right)-U_{n-1}\left(x\right)\)
כלומר ההבדל היחיד הוא ה-2 ב-\(U_{1}\left(x\right)=2x\) . זה נותן לנו:

\(U_{1}\left(\frac{x-2}{2}\right)=x-2\)
וזה... עדיין לא מה שאנחנו צריכים! כי אנחנו רוצים את \(p_{1}\left(x\right)=x-1\) ! אבל אפשר להוסיף פה אקסטרה התחכמות אם שמים לב לכך ש-\(U_{0}\left(\frac{x-2}{2}\right)=1\) , כלומר

\(U_{1}\left(\frac{x-2}{2}\right)+U_{0}\left(\frac{x-2}{2}\right)=x-1=p_{1}\left(x\right)\)
ואם נסמן \(U_{-1}\left(x\right)=0\) נקבל גם

\(U_{0}\left(\frac{x-2}{2}\right)+U_{-1}\left(\frac{x-2}{2}\right)=1=p_{0}\left(x\right)\)
מה שיפה הוא שצירוף לינארי של אובייקטים שמקיימים נוסחת נסיגה יקיים את אותה נוסחת הנסיגה. אז נקבל באופן כללי:

\(p_{k}\left(x\right)=U_{k}\left(\frac{x-2}{2}\right)+U_{k-1}\left(\frac{x-2}{2}\right)\)
ולסיום:

\(L_{G}=\left(x-1\right)p_{n-1}\left(x\right)-p_{n-2}\left(x\right)=\)

\(=\left(x-1\right)U_{n-1}\left(\frac{x-2}{2}\right)+\left(x-1\right)U_{n-2}\left(\frac{x-2}{2}\right)-U_{n-2}\left(\frac{x-2}{2}\right)-U_{n-3}\left(\frac{x-2}{2}\right)=\)

\(=\left(x-1\right)U_{n-1}\left(\frac{x-2}{2}\right)+\left(x-2\right)U_{n-2}\left(\frac{x-2}{2}\right)-U_{n-3}\left(\frac{x-2}{2}\right)\)
הגענו עכשיו לביטוי שאפשר לפשט חלק נכבד ממנו, אם כי אולי קשה לראות את זה כרגע. ניקח את החלק הזה:

\(\left(x-2\right)U_{n-2}\left(\frac{x-2}{2}\right)-U_{n-3}\left(\frac{x-2}{2}\right)\)
וכדי שיהיה ברור מה אפשר לעשות פה, נסמן \(t=\frac{x-2}{2}\) , כלומר קיבלנו

\(2tU_{n-2}\left(t\right)-U_{n-3}\left(t\right)=U_{n-1}\left(t\right)=U_{n-1}\left(\frac{x-2}{2}\right)\)
כלומר, קיבלנו

\(\left(x-1\right)U_{n-1}\left(\frac{x-2}{2}\right)+\left(x-2\right)U_{n-2}\left(\frac{x-2}{2}\right)-U_{n-3}\left(\frac{x-2}{2}\right)=\)

\(=\left(x-1\right)U_{n-1}\left(\frac{x-2}{2}\right)+U_{n-1}\left(\frac{x-2}{2}\right)=xU_{n-1}\left(\frac{x-2}{2}\right)\)
אחרי כל המהומה הזו, הנוסחה הסופית כמעט טריוויאלית: \(L_{G}=xU_{n-1}\left(\frac{x-2}{2}\right)\) . גם אם איבדתם אותי בדרך, זה מה שאנחנו צריכים - קיבלנו שהלפלסיאן של השרוך מאורך \(n\) הוא \(xU_{n-1}\left(\frac{x-2}{2}\right)\) כש-\(U_{n-1}\) הוא פולינום צ'בישב מן הסוג השני. עכשיו השאלה היא רק מה הערכים העצמיים של זה - כלומר, מה השורשים של הפולינום הזה. בבירור 0 הוא שורש - זו המשמעות של הכפל ב-\(x\) , אבל כבר ידענו ש-0 הוא שורש. שאר השורשים הם השורשים של \(U_{n-1}\left(\frac{x-2}{2}\right)\) - כלומר, אם \(t\) הוא שורש של \(U_{n-1}\) אז נסמן \(t=\frac{x-2}{2}\) ונקבל ש-\(x=2t+2\) הוא שורש של \(L_{G}\) .

מי השורשים של פולינומי צ'בישב? קל להבין את זה עבור \(T_{n}\) , הפולינום מהסוג הראשון. ראינו איך הוא נבנה בצורה שתבטיח שיתקיים הדבר הבא:

\(T_{n}\left(\cos\theta\right)=\cos\left(n\theta\right)\)
כאן \(T_{n}\) הוא פולינום ממעלה \(n\) ולכן יש לו \(n\) שורשים לכל היותר - ומהנוסחה הזו קל למצוא \(n\) שורשים שונים שכאלו. קוסינוס זו פונקציה שאנחנו מבינים מצוין ויודעים בדיוק איפה השורשים שלה - \(\cos\left(x\right)=0\)
אם ורק אם \(x=\frac{\pi}{2}+k\pi\) כאשר \(k\in\mathbb{Z}\) (הנה פוסט שלי על סינוסים וקוסינוסים שממנו אפשר להבין את זה) ואת זה אפשר לכתוב גם בתור \(x=\left(2k+1\right)\frac{\pi}{2}\) . אז בואו נסתכל על סדרה \(\theta_{0},\theta_{1},\ldots,\theta_{n-1}\) של ערכים כך ש-\(\theta_{k}=\frac{2k+1}{n}\frac{\pi}{2}\) ; מובטח לנו ש-

\(T_{n}\left(\cos\left(\theta_{k}\right)\right)=\cos\left(n\theta_{k}\right)=\cos\left(\left(2k+1\right)\frac{\pi}{2}\right)=0\)
כדי לראות שכל השורשים הללו שונים זה מזה, נשים לב לכך ש-\(\theta_{0}=\frac{\pi}{2}\)
ו-\(\theta_{n-1}=\frac{2n-1}{n}\frac{\pi}{2}\lt \pi\) , כלומר כל ה-\(\theta\) -ות הללו חיות בתוך הקטע \(\left[\frac{\pi}{2},\pi\right]\) שבו \(\cos\)
היא פונקציה מונוטונית יורדת - ולכן \(\cos\left(\theta_{0}\right),\ldots\cos\left(\theta_{n-1}\right)\)
הם כולם ערכים שונים זה מזה, ומכאן שאלו כל השורשים של \(T_{n}\) .

יופי, אבל רצינו את \(U_{n}\) . פשוט קל יותר להבין את \(T_{n}\) . השאלה היא איזו נוסחה דמויית \(T_{n}\left(\cos\theta\right)=\cos\left(n\theta\right)\) מתקיימת עבור \(U_{n}\) . אז בואו ננסה להבין את זה - מהו \(U_{n}\left(\cos\theta\right)\) ?

ראשית, \(U_{0}\left(\cos\theta\right)=1\) , זה בדיוק כמו עם \(T_{0}\) . ההבדל הוא ב-\(U_{1}\left(x\right)=2x\) . כלומר, \(U_{1}\left(\cos\theta\right)=2\cos\theta\) . עכשיו, מה אני אמור לעשות עם \(2\cos\theta\) ? את מה זה מזכיר לי? ובכן, זה מזכיר לי במעורפל את הזהות הטריגונומטרית

\(\sin2\theta=2\sin\theta\cos\theta\)
כלומר:

\(2\cos\theta=\frac{\sin2\theta}{\sin\theta}\)
כאשר כאן סימן החילוק מסתיר את המקרה הפרטי המיוחד שבו \(\theta=\pi k\) , מה שמאפס גם את המונה וגם את המכנה. במקרה הזה אני פשוט מגדיר \(\frac{\sin2\theta}{\sin\theta}=2\) (יש לזה הצדקה - קל לראות עם כלל לופיטל ש-\(\lim_{\theta\to\pi k}\frac{\sin2\theta}{\sin\theta}=2\) ).

אז קיבלנו:

\(U_{1}\left(\cos\theta\right)=\frac{\sin2\theta}{\sin\theta}\)
וגם מתקיים

\(U_{0}\left(\cos\theta\right)=\frac{\sin\theta}{\sin\theta}\)
האם זה משהו שיכול להמשיך עם הרקורסיה הרגילה של פולינומי צ'בישב? ננסה להוכיח באינדוקציה ש-\(U_{n}\left(\cos\theta\right)=\frac{\sin\left(\left(n+1\right)\theta\right)}{\sin\theta}\) :

\(U_{n}\left(\cos\theta\right)=2\cos\theta U_{n-1}\left(\cos\theta\right)-U_{n-2}\left(\cos\theta\right)=\)

\(=2\cos\theta\frac{\sin\left(n\theta\right)}{\sin\theta}-\frac{\sin\left(\left(n-1\right)\theta\right)}{\sin\theta}=\frac{2\cos\theta\sin\left(n\theta\right)-\sin\left(\left(n-1\right)\theta\right)}{\sin\theta}\)
עכשיו נשתמש בזהות \(2\cos\theta\sin\varphi=\sin\left(\theta+\varphi\right)+\sin\left(\varphi-\theta\right)\)
כדי לקבל

\(\frac{2\cos\theta\sin\left(n\theta\right)-\sin\left(\left(n-1\right)\theta\right)}{\sin\theta}=\frac{\sin\left(\left(n+1\right)\theta\right)+\sin\left(\left(n-1\right)\theta\right)-\sin\left(\left(n-1\right)\theta\right)}{\sin\theta}=\frac{\sin\left(\left(n+1\right)\theta\right)}{\sin\theta}\)
הצלחה! אז קיבלנו את הנוסחה \(U_{n}\left(\cos\theta\right)=\frac{\sin\left(\left(n+1\right)\theta\right)}{\sin\theta}\) . אנחנו כזכור רוצים את השורשים של \(U_{n-1}\left(\cos\theta\right)=\frac{\sin\left(n\theta\right)}{\sin\theta}\)
מה שטיפה מפשט לנו את הכתיבה - כל מה שאנחנו צריכים הוא למצוא מה \(n-1\)
הערכים שמאפסים את \(\sin\left(n\theta\right)\) ולא מאפסים את \(\sin\theta\) . סינוס הוא קל יותר מקוסינוס - הוא מתאפס בכל \(\theta=\pi k\) , ולכן אנחנו צריכים את השורשים \(\theta_{1},\ldots,\theta_{n-1}\) המוגדרים על ידי \(\frac{k}{n}\pi\) . מצאנו את היעד שלנו! הערכים שמאפסים את \(U_{n-1}\) הם מהצורה \(\cos\left(\frac{k}{n}\pi\right)\) ולכן הערכים שמאפסים את \(L_{G}\) הם מהצורה \(2\cos\left(\frac{k}{n}\pi\right)+2\) . אלו הערכים העצמיים שחיפשתי!

...

בואו נפשט את זה עוד קצת.

בגדול מה שמפריע לי, כי אני ממש קטנוני, זה שיש לנו ביטוי עם חיבור. לא רוצה. כדי לפשט את זה אני שוב פושט על רשימת הזהויות הטריגונומטריות ומחפש משהו שיעזור לי. למרבה השמחה, יש כזה:

\(\cos^{2}x=\frac{1+\cos2x}{2}\)
או במילים אחרות:

\(1+\cos2x=2\cos^{2}x\)
נכפול את הכל ב-\(2\) ונקבל באגף שמאל בדיוק את מה שרציתי לפשט:

\(2\cos2x+2=4\cos^{2}x\)
עכשיו נציב \(x=\frac{k\pi}{2n}\) ונקבל:

\(2\cos\left(\frac{k}{n}\pi\right)+2=4\cos^{2}\left(\frac{k\pi}{2n}\right)\)
וזהו! זה מה שהבטחתי בהתחלה! הערכים העצמיים של \(L_{P_{n}}\) עבור השרוך מאורך \(n\) הם 0 וכל הערכים מהצורה \(4\cos^{2}\left(\frac{k\pi}{2n}\right)\)
עבור \(1\le k\le n-1\) . זה מסיים את כל ההוכחות הכבדות ומשאיר רק את הסיכום.

אז מה ראינו פה בעצם?

זה היה פוסט ארוך ועמוס בשלל נושאים, אז רגע לפני הסיום בואו נעשה סיכום של מה שהלך פה בעצם. 1. רצינו לספור כמה מבוכים יש מסדר \(n\times m\) (עבור הגדרה ספציפית של "מבוך").

1. ראינו שזו בעיה שקולה לבעיה של ספירת עצים פורשים של גרף \(G\) מסוים.

2. ראינו שספירת עצים פורשים שקולה לבעיה של חישוב דטרמיננטה של מינור של הלפלסיאן \(L_{G}\) .

3. ראינו שכדי לחשב את הדטרמיננטה הזו מספיק למצוא את הערכים העצמיים השונים מאפס של \(L_{G}\) .

4. ראינו ש-\(G=P_{n}\square P_{m}\) כש-\(\square\) הוא הסימון למכפלה של גרפים.

5. ראינו שנובע מזה ש-\(L_{G}=L_{P_{n}}\oplus L_{P_{m}}\) כש-\(\oplus\)
   הוא הסימון של סכום קרונקר של מטריצות.

6. ראינו שנובע מזה שהערכים העצמיים של \(L_{G}\) הם סכומים של הערכים העצמיים של \(L_{P_{n}},L_{P_{m}}\) .

7. ראינו שהערכים העצמיים של \(L_{P_{n}}\) ששונים מאפס הם מהצורה \(4\cos^{2}\left(\frac{k\pi}{2n}\right)\)
   עבור \(k=1,2,\ldots,n-1\) .

בואו נרכיב את כל זה ביחד כדי לקבל את הנוסחה שפותרת את הבעיה. ראשית, מה שראינו בשלב 4 הוא זה: שאם הערכים העצמיים של הלפלסיאן הם \(0=\lambda_{0},\lambda_{1},\ldots,\lambda_{t-1}\) אז הדטרמיננטה של כל מינור שלו היא \(\frac{1}{t}\lambda_{1}\cdots\lambda_{t-1}\) - מכפלת כל הערכים העצמיים חוץ מ-0, וחלוקה ב-\(t\) שהוא המספר הכולל של ערכים עצמיים.

עכשיו, נסמן את הערכים העצמיים של \(P_{n}\) ב-\(0=\tau_{0},\tau_{1},\ldots,\tau_{n-1}\) . בואו נשתמש בתוצאה על מכפלת הערכים העצמיים השונים מאפס על הגרף הזה. זה גרף שרוך, ושרוך הוא בעצמו עץ, כלומר קיים לו בדיוק עץ פורש יחיד - זה אומר שמתקיים \(\frac{1}{n}\prod_{k=1}^{n-1}\tau_{k}=1\) . באופן דומה עבור \(P_{m}\) נסמן את הערכים העצמיים ב-\(0=\rho_{0},\rho_{1},\ldots,\rho_{m-1}\) ונקבל שמתקיים \(\frac{1}{m}\prod_{h=1}^{m-1}\tau_{h}=1\) . שני אלו הולכים לסייע לי עוד מעט.

עכשיו מצאנו את הערכים המפורשים של הערכים העצמיים הללו בשלב 8 ועוד נציב אותם, אבל זה יהיה בהמשך. בינתיים נשתמש בשלב 7 כדי להסיק שמתקיים ש-\(t=mn\) , ושכל ערך עצמי הוא מהצורה \(\lambda_{kh}=\tau_{k}+\rho_{h}\)
עבור \(0\le k\lt n\) ו-\(0\le h\lt m\) . אז בעצם יש לנו שלושה סוגים שונים של ערכים עצמיים: - הערך העצמי \(\lambda_{00}=\tau_{0}+\rho_{0}=0\) - לא מפתיע שהוא קיים, לכל לפלסיאן יש ערך עצמי 0.

• הערכים העצמיים מהצורה \(\lambda_{k0}=\tau_{k}\) ו-\(\lambda_{0h}=\rho_{h}\)

• אלו שהם פשוט הערכים העצמיים של אחד משני הגרפים \(P_{n},P_{m}\) .

• כל היתר: \(\lambda_{kh}=\tau_{k}+\rho_{h}\) עבור \(1\le k\lt n\) ו-\(1\le h\lt m\) .

עכשיו נציב ב-\(\frac{1}{t}\lambda_{1}\cdots\lambda_{t-1}\) את כל הערכים העצמיים חוץ מ-\(\lambda_{00}\) שלא משתתף בנוסחה הזו, כשבמקום אינדקס רץ בודד \(t\) אני משתמש באינדקסים \(k,h\) כמו קודם. אבל - אני אפריד את הערכים העצמיים מהצורה \(\lambda_{0h},\lambda_{k0}\) מכל היתר. נקבל:

\(\frac{1}{mn}\prod_{k=1}^{n-1}\lambda_{k0}\cdot\prod_{h=1}^{m-1}\lambda_{0m}\cdot\prod_{k=1}^{n-1}\prod_{h=1}^{m-1}\lambda_{hk}\)
עכשיו, מה זה \(\prod_{k=1}^{n-1}\lambda_{k0}\) ? זו פשוט המכפלה \(\prod_{k=1}^{n-1}\tau_{k}\) של כל הערכים העצמיים השונים מאפס של הגרף\(P_{n}\) . אם נכפול אותה ב-\(\frac{1}{n}\) שנמצא שם נקבל \(\frac{1}{n}\prod_{k=1}^{n-1}\tau_{k}=1\) . באופן דומה נשתמש גם ב-\(\frac{1}{m}\prod_{h=1}^{m-1}\tau_{h}=1\) , ועכשיו הביטוי הפך להיות משמעותית יותר פשוט:

\(\prod_{k=1}^{n-1}\prod_{h=1}^{m-1}\lambda_{hk}=\prod_{k=1}^{n-1}\prod_{h=1}^{m-1}\left(\tau_{k}+\rho_{h}\right)\) עכשיו זה זמן טוב להציב את הערכים המפורשים:

\(\prod_{k=1}^{n-1}\prod_{h=1}^{m-1}\left(4\cos^{2}\left(\frac{k\pi}{2n}\right)+4\cos^{2}\left(\frac{h\pi}{2m}\right)\right)\)
וזהו! קיבלנו את הנוסחה מתחילת הפוסט!

\(T\left(n,m\right)=\prod_{k=1}^{n-1}\prod_{h=1}^{m-1}\left(4\cos^{2}\left(\frac{k\pi}{2n}\right)+4\cos^{2}\left(\frac{h\pi}{2m}\right)\right)\)
האם סיימנו? סוג של... יש לנו נוסחה סגורה יפה, אבל אני עדיין רוצה לחשב את הפתרון למקרה הקונקרטי שלי, \(423\times855\) . אם אני אנסה סתם לחשב את זה בפייתון זה לא יעבוד - הולכים לצאת מספרים גדולים מדי והוא לא יצליח לעבוד איתם (כשאני עובד עם הספרייה numpy אני אקבל את התוצאה המרגשת np.float64)inf( - ניסיתי).

אז אני אשתמש בטריק אחד אחרון ואוציא לוגריתם לשני האגפים. היופי בלוגריתמים הוא שהם הופכים מכפלות לסכומים, ולכן המספר שאני אקבל יהיה קטן משמעותית:

\(\log T\left(n,m\right)=\sum_{k=1}^{n-1}\sum_{h=1}^{m-1}\log\left(4\cos^{2}\left(\frac{k\pi}{2n}\right)+4\cos^{2}\left(\frac{h\pi}{2m}\right)\right)\)
אבל מה המשמעות של מספר כזה? בואו ניקח לדוגמא את \(17,138,194\)
וניקח לו לוגריתם על בסיס 10 (שאני פשוט אסמן ב-\(\log\) ):

\(\log17138194=7.233965054625744\)
מה שקיבלנו פה הוא בעצם שני מספרים: ה-7 מספר לנו כמה ספרות יש במספר שלנו - יותר במדויק, הוא אומר שהמספר שלנו גדול מ-\(10^{7}\)
אבל קטן מ-\(10^{8}\) , כלומר יש בו 8 ספרות (הוא קטן יותר מ-1 שאחריו 8 אפסים, כלומר המספר הקטן ביותר עם 9 ספרות). כל ה-\(.233965054625744\) שאחרי הנקודה מספר לנו בכמה צריך לכפול את \(10^{7}\) כדי "לתקן" אותו ולקבל את המספר המדויק \(17138194\) . ליתר דיוק, לא צריך לכפול את \(10^{7}\) במספר הזה אלא ב-10 בחזקת המספר הזה, מה שיוצא בערך \(1.7138194\) . למה זה עובד? פשוט כי אם באופן כללי \(\log a=n+x\) כאשר \(n\in\mathbb{N}\) ו-\(0\le x\lt 1\) , אז

\(a=10^{\log a}=10^{n+x}=10^{n}\cdot10^{x}\)
מכיוון ש-\(x\lt 1\) אז \(10^{x}\) הוא מספר קטן מ-10. זה מוביל אותנו לשיטה שבה אוהבים לתאר מספרים גדולים בצורה לא מדויקת: אם נסמן \(m=10^{x}\) , אז נקבל \(a=m\cdot10^{n}\) - כאן המספר \(m\) נקרא מנטיסה ואילו \(n\) נקרא אקספוננט ובמחשב נכתוב דברים כמו "1.7138e7" כדי לתאר את זה. אז אני לא באמת צריך לחשב את המספר המפלצתי שלי - אני צריך לחשב את הלוגריתם שלו, לקחת את הערך השלם שלו בתור האקספוננט, להעלות בחזקת 10 את היתר ולקבל את המנטיסה, להדפיס את זה יפה וסיימנו.

הנה קוד פייתון שמבצע את כל החישוב ב-4 שניות במחשב המקרטע שלי:

import numpy as np
import itertools
n = 423
m = 855
vals = [np.log10(4*(np.cos(k*np.pi/(2*n)))**2 + 4*(np.cos(h*np.pi/(2*m)))**2)
 for (k,h) in itertools.product(range(1,n), range(1,m))
 ]
a = sum(vals)
n = int(a)
m = 10**(a - n)
print(f"{m}e{n}")

והתוצאה היא... תחזיקו חזק... זה:

3.142182277684719e182690

מה המספר הזה אומר, בעצם? כלום. פשוט כלום. אני לא רואה שום דבר שאפשר לעשות עם הידע הזה. זה סתם רצף אקראי של ספרות. אבל מה שיפה זה שאם אחרים ינסו לבצע את אותו חישוב, אבל בשיטות השונות שלהם, בסופו של דבר נגיע לאותו רצף ספרות אקראי ותתחזק אצלנו עוד יותר התחושה שמה שעשינו הוא נכון - שהנוסחה המגוחכת שהגענו אליה היא נכונה.

בואו נסתכל עליה שוב:

\(\log T\left(n,m\right)=\sum_{k=1}^{n-1}\sum_{h=1}^{m-1}\log\left(4\cos^{2}\left(\frac{k\pi}{2n}\right)+4\cos^{2}\left(\frac{h\pi}{2m}\right)\right)\)
אם היו שואלים אותי על מבוכים לפני שהכרתי את כל הסיפור הזה ואז מראים לי את הנוסחה, הייתי חושב שהעולם השתגע ולא מבין מאיפה זה בא בכלל. אז בפוסט הזה ראינו בפירוט ניכר בדיוק מאיפה זה בא בכלל, ועכשיו אני מרגיש די מיודד עם הנוסחה הזו ועם מבוכים באופן כללי. כנראה שהנוסחה האמיתית הייתה המתמטיקה שפגשנו בדרך.