מה הקטע עם השלמת סדרות ואיך זה קשור לאינטרפולציה פולינומית?

ברשתות החברתיות יש הרבה סוגי שיקוצים שכל מטרתם היא למשוך אנשים כדי שיגיבו ואפילו טוב מכך - שיריבו, כי ריבים וסבל והרס שווים כסף עבור יוצרי השיקוצים הללו. ואחד מהשיקוצים הנאלחים ביותר הן חידות "מתמטיות" של השלמת סדרות. לדוגמא, זו:

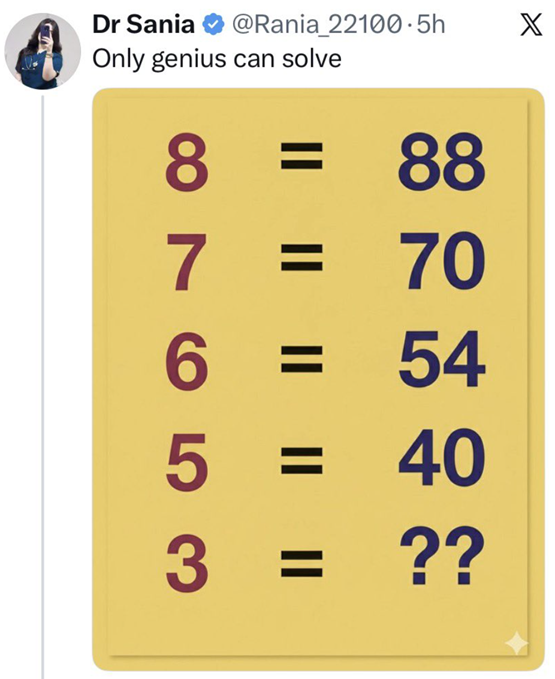
יש כאן כמה דברים ממש מעצבנים עבורי: משפט המחץ על "רק גאון יכול לפתור", סכמת הצבעים הגועלית, השימוש הלא נכון בסימן "=" - אבל כל אלו שטויות, הדברים הללו מהונדסים כדי לעצבן וכדי שנגיב (אבל לא תגובה כמו שלי, של תלונה בבלוג, אלא תגובה לציוץ המקורי בטוויטר כדי להכניס כסף ליוצרים שלו). מעבר לדברים המעצבנים הללו, מה התוכן המתמטי שיש כאן? ובכן, זה משהו שעתיק בהרבה מהרשתות החברתיות - בעיה שבה מציגים לנו סדרה כלשהי של מספרים ושואלים מה האיבר הבא בסדרה. אבל צריך קצת להיזהר - כאן יש שתי סדרות של מספרים. בעצם, מראים לנו מין התאמה שכזו בין המספר מצד שמאל למספר מצד ימין, ואנחנו צריכים להבין את החוקיות של ההתאמה הזו וליישם את החוקיות הזו על האיבר האחרון.

תגובה נפוצה שלי על חידות כאלו היא שזה הכל בולשיט כי כל התאמה היא אפשרית. הרי כל ניחוש שלנו לגבי החוקיות כאן הוא ניחוש בלבד, ויש הרבה סדרות מספרים שבהן נדמה לנו שיש כלל טבעי נחמד אבל בעצם יש המון כללים אפשריים שנותנים תוצאות שונות. למשל, נניח שאני נותן את הסדרה \(2,3,5,7,11\) ושואל מה האיבר הבא - לכאורה נראה ש-13 מתאים (זו התשובה שאני הייתי נותן) כי הסדרה כללה את כל המספרים הראשוניים עד וכולל 11 והבא בתור הוא 13. אבל בעצם, גם 101 מתאים אם אנחנו לא רוצים סתם מספרים ראשוניים אלא מספרים ראשוניים פלינדרומיים, כאלו שנכתבים בייצוג עשרוני בצורה כזו שאם הם נקראים מימין או משמאל הם אותו הדבר. או שאולי 17 הוא האיבר הבא בתור שמתאים כי הסדרה היא בכלל\(\left\lfloor \frac{3^{n}}{2^{n}}\right\rfloor\) עבור \(n=2,3,4,5,6,7\) ? ואולי האיבר הבא הוא 16 כי הסדרה סופרת כמה עלים יכולים להיות בעץ בינארי? את כל הדוגמאות הללו לא טרחתי להמציא - נכנסתי לאתר המופלא של האנציקלופדיה לסדרות מספרים, הקלדתי \(2,3,5,7,11\) ובדקתי אילו השלמות הזויות הוא ימצא לי. ככה זה - העולם גדול ורחב ומעניין וההמשך ה"טבעי" שאנחנו חושבים עליו הוא לאו דווקא מה שחשבו עליו כשיצרו את הסדרה.

אבל בואו ננסה לגשת לחידות הללו מנקודת מבט חיובית: נניח שכן יש פתרון אחד שהוא הרבה יותר סביר מכל פתרון אחר, וננסה למצוא אותו. הנה חידה שכזו, וריאציה על הסגנון של החידה הקודמת:

אני אסביר בסוף את הפתרון של החידה הזו. בואו ננסה עכשיו לחשוב מה יכול להיות הפתרון של החידה הקודמת, זו שבה סדרת המספרים היא:

\(88,70,54,40,??\)

כשיש לנו סדרות של מספרים ואנחנו רוצים לדעת מה האיבר הבא, השאלה שאנחנו שואלים היא - נניח שהסדרה היא הדבר הכי פשוט שיכול להיות מבין כל מה שתואם את המספרים שאנחנו רואים - מהו הדבר הפשוט הזה?

הסדרה הכי פשוטה היא זו שבה כל הערכים הם קבועים, כלומר למשל \(42,42,42,42,\ldots\) . אבל זו לא סדרה כזו מעניינת. דרך אחת לגוון היא שכל איבר יהיה שווה לאיבר הקודם ועוד משהו. לסדרה כזו קוראים "סדרה חשבונית". למשל הסדרה \(2,12,22,33,42,\ldots\) היא כזו: כל איבר בה שווה לאיבר הקודם ועוד 10. סדרות כאלו לא חייבות לעלות, הן יכולות גם לרדת. למשל \(78,66,54,42,\ldots\) היא סדרה שכל איבר בה שווה לאיבר הקודם ועוד \(-12\) , כלומר פחות 12.

האם הסדרה \(88,70,54,40\) היא חשבונית? לא, כי בואו נסתכל על הסדרה שמתקבלת ממנה כשלוקחים את ההפרש בין כל זוג איברים סמוך:

\(-18,-16,-14,\ldots\)

אבל - אה-הא! הסדרה הזו של ההפרשים היא כן סדרה חשבונית! בכל פעם מוסיפים 2 לאיבר הבא! אז אפשר לנחש שההפרש הבא יהיה \(-12\) ! ולכן, אם מוסיפים \(-12\) אל \(40\) שהיה האיבר האחרון שראינו, מקבלים \(28\) ולכן זה הפתרון!

נשמע סביר והגיוני? זה באמת סביר והגיוני! אבל נפלתי במלכודת. זכרו, החידה המקורית לא הייתה שעשוע מחשבה חביב למען רווחת הציבור; היא כלי שאנשים מניפולטיביים משתמשים בו כדי לעורר מהומות שיכניסו לכיסם כסף. אי לכך ובהתאם לזאת, החידה הזו כללה הטרלה: הטעיה מהסוג הניג'סי ביותר. כי אם נסתכל על העמודה השמאלית של המספרים, כתוב שם \(8,7,6,5,3\) - שמים לב לקפיצה? ועכשיו יש שלושה סוגי פותרים: 1. פותרים שבכלל לא מתעניינים במה שקורה בעמודה השמאלית. מבחינתם מה שמגדיר את הסדרה הוא מה שיש בעמודה הימנית וזהו ולכן הפתרון הוא 28.

1. פותרים שרואים בעמודה השמאלית סוג של אינדקס ולכן אם קפצנו מ-5 אל 3 זה אומר שקפצנו על איבר, והאיבר הבא בתור אמור להיות 18 (למה? בשלב הזה כבר אפשר להבין) ולכן זה הפתרון.

2. פותרים שחושבים כמו האלו מ-2 אבל פשוט פספסו או שכחו את הקפיצה הזו וחושבים במובלע שכתוב שם 4 ולכן לדעתם התשובה אמורה להיות 28 והם ירגישו מה-זה מטומטמים כשיבינו שעבדו עליהם.

בגלל שיש כאן שתי תשובות לגיטימיות, זה מזמין ויכוחים ומהומות בין שני צדדים שכל אחד לשיטתו צודק לגמרי - ועוד גל של אנשים ש"טועים"ואחרים שיתקנו אותם, ואז הטועים יגידו וואי וואי וואי איזה טיפשים היינו ועוד ועוד מלל יישפך על הבעיה המיותרת הזו כדי שנצלן אינטרנטי כלשהו יקבל עוד כמה גרושים. כל זה לא חדש, זה כמו המהומות סביב המשוואה \(6\div2(1+2)\) שכתבתי עליה פעם פוסט.

אבל אני רוצה לנצל את החידה הזו בצורה פרודקטיבית, כדי להציג משהו נחמד במתמטיקה. אז בשביל זה, בואו נפסיק לחשוב על \(88,70,54,40,??\) סתם בתור "סדרה"ונחשוב עליה בתור "התאמה": אנחנו מתאימים ל-8 את 88, ול-7 את 70 וכן הלאה. להתאמות כאלו יש שם במתמטית: פונקציות. אני מסמן פונקציה עם סימון כמו \(f\left(x\right)\) שאומר "\(x\) הוא משתנה, אפשר להציב בו ערכים שונים ומשונים, ו-\(f\) זה הסימון שמתאר את הפונקציה עצמה וכשאני מציב ערך קונקרטי ב-\(x\) היא מחזירה לי תוצאה קונקרטית". במקרה שלנו זה ייראה כך:

\(f\left(8\right)=88\)

\(f\left(7\right)=70\)

\(f\left(6\right)=54\)

\(f\left(5\right)=40\)

\(f\left(3\right)=??\)

לכתוב פונקציה על ידי כך שכותבים את כל הערכים שלה במפורש זה מעייף. השאלה המעניינת היא האם יש דרך פשוטה לכתוב פונקציה, ולעתים קרובות יש. בואו נסתכל לרגע על הסדרה \(2,12,22,33,42,\ldots\) . נניח שהטור השמאלי של מספרים שמתאים לה הוא \(0,1,2,3,4,\ldots\) . במקרה הזה, קל לכתוב את הפונקציה שיוצרת את ההתאמה בין שני הטורים:

\(f\left(x\right)=10x+2\) מה זה אומר? זה מתכון לאיך ליצור את הפלט בהינתן הקלט. נתנו לנו \(x\) ? נכפיל אותו ב-10 ונוסיף 2 לתוצאה. למשל \(f\left(3\right)=10\cdot3+2=32\) . זה עובד תמיד - קיבלנו כתיב קומפקטי יחסית עבור הסדרה הזו.

האם אפשר לעשות את זה עבור החידה המקורית? הנה דרך לנסות לגלות. בואו נשתמש באותיות \(a,b\) כדי לסמן מה שנקרא פרמטרים - ערכים מספריים שאני לא מתחייב עליהם כרגע. עכשיו אני אכתוב את הפונקציה בעזרת הפרמטרים:

\(f\left(x\right)=ax+b\) הפונקציה \(f\left(x\right)=10x+2\) שראינו לפני רגע התקבלה עבור הפרמטרים \(a=10\) ו-\(b=2\) , אבל כל הצבה של ערכים שונים לפרמטרים תניב לנו פונקציה שונה. מה ההבדל בין "משתנה"ובין "פרמטר"? אין הבדל עקרוני, פשוט אנחנו חושבים על הפרמטרים בתור משהו שאנחנו מציבים בו ערכים כדי לקבל פונקציה מתוך משפחה גדולה של פונקציות, ועל המשתנים בתור משהו שאנחנו מציבים בו ערך אחרי שכבר יש לנו ביד פונקציה קונקרטית, ואנחנו רוצים לדעת מה היא מחזירה על קלט קונקרטי.

יופי, אז אני מסמן \(f\left(x\right)=ax+b\) . עכשיו, אני יודע ש-\(f\left(8\right)=99\) אז אם אני אציב את זה בנוסחה אני אקבל

\(8a+b=88\) זה נותן לנו קשר כלשהו שצריך להתקיים בין \(a,b\) אבל יש המון דרכים שונות לקיים אותו. למשל, \(a=10,b=8\) . או למשל, \(a=0,b=88\) . זה יותר מדי חופש, אז בואו ננסה לבדוק איזה קשר \(f\left(7\right)=70\) מציע:

\(7a+b=70\) עכשיו קיבלנו מערכת של שתי משוואות בשני משתנים. אפשר לנקוט בתעלול נפוץ - נחסר את המשוואה השניה מהראשונה, מה שייתן לנו

\(a=18\) ועכשיו אפשר להסיק מהמשוואה הראשונה לבדה ש-\(b=-56\) , כלומר הפונקציה שלנו היא \(f\left(x\right)=18x-56\) ...? זה היה... מפתיע? זה בהחלט לא היה הדבר הראשון שחשבנו עליו. אבל כן, אפשר להוכיח את זה (ואסביר בהמשך גם איך) - אם יש פונקציה מהצורה \(f\left(x\right)=ax+b\) שמתארת את הסדרה שבחידה, זו חייבת להיות הפונקציה הזו.

רק שלרוע המזל, היא לא. אם נציב \(x=6\) נקבל \(f\left(x\right)=52\) וזה, מה לעשות, לא ה-54 שהיינו אמורים לקבל. כל מה שעשינו כרגע קרס ונחרב בקול רעש גדול. פשוט לא קיימת פונקציה מהצורה \(f\left(x\right)=ax+b\) שמחזירה את הסדרה הזו.

אז בואו נתפשר על פונקציה קצת פחות פשוטה. כשמסתכלים על משהו כמו \(f\left(x\right)=10x+2\) , אילו פעולות בעצם ביצענו עם \(x\) המסכן? הרשינו לחבר לו מספר כלשהו (וגם לחסר - אם היינו מחברים מספר שלילי). גם הרשינו לכפול אותו במספר קבוע כמו 10 (ואם היינו כופלים ב-\(\frac{1}{2}\) זה היה כמו לחלק ב-2). מה שלא עשינו היה להרשות ל-\(x\) לבצע פעולות עם עצמו. עכשיו, אם אני מחבר את \(x\) עם עצמו אני מקבל \(x+x=2x\) וזה כאילו כפלתי אותו ב-2 ואת זה אנחנו כבר מרשים, אז זה לא מעניין. אבל מה אם אני יכול לכפול את \(x\) בעצמו? אני אקבל את \(x^{2}\) , וזה כבר משהו חדש. אולי פונקציה מהצורה \(f\left(x\right)=ax^{2}+bx+c\) כן תעבוד לנו?

אפשר לעשות בדיוק את מה שעשינו קודם - להציב ערכים קונקרטיים בנוסחה הכללית הזו ולחלץ מהם קשרים בין \(a,b,c\) . יש לנו שלושה משתנים אז נזדקק לשלוש משוואות. אני אציב את \(x=8,7,6\) , אפשט ואקבל

\(64a+8b+c=88\)

\(49a+7b+c=70\)

\(36a+6b+c=54\)

נחסר את המשוואה השניה מהראשונה, ואת השלישית מהשניה, ונקבל

\(15a+b=18\)

\(13a+b=16\)

נחסר את המשוואה השניה מהראשונה ונקבל

\(2a=2\)

כלומר

\(a=1\)

התקדמנו! נציב את זה בשתי המשוואות שקיבלנו לפני רגע ונקבל

\(15+b=18\)

\(13+b=16\)

כלומר

\(b=3\)

התקדמנו! נציב את זה ב-\(64a+8b+c=88\) שממנה התחלנו, ונקבל

\(64+24+c=88\)

כלומר

\(c=0\)

היי, זה יצא די פשוט! קיבלנו את הפונקציה \(f\left(x\right)=x^{2}+3x\) . אם אציב \(x=3\) אקבל \(f\left(3\right)=9+9=18\) , וזו אכן התשובה ה"נכונה". יופי!

האם היה אפשר להגיע לזה יותר בקלות? בוודאי. כשאני ראיתי את החידה לא פתרתי אותה ככה. אמרתי לעצמי - "יש פה \(8\) ו-\(88\) , כלומר \(8\) כפול 11. אה, השורה הבאה זה 7 כפול 10. הבנתי את הקטע, מה שכופלים בו גם כן קטן ב-1. ההפרש ביניהם יישאר 3 באופן קבוע, כלומר זו המכפלה \(x\left(x+3\right)\) ."זו בהחלט דרך סבירה להגיע לפתרון ואני מנחש שרוב הפותרים עושים משהו כזה, אבל מה שחשוב לי להדגיש פה הוא שיש דרך מסודרת להגיע לפתרון - בדיוק באמצעות כתיבת מערכת המשוואות שהצגתי. העניין הוא שיש דרך אפילו עוד יותר מסודרת ובמובן מסוים עוד יותר קלה להגיע לפתרון הזה - מה שנקרא אינטרפולציה פולינומית.

יש כאן שתי מילים מפחידות, נתחיל עם השניה. פולינום זה מה שמקבלים כשיש לנו ביד \(x\) ואנחנו מתעללים בו בדרכים שכבר ראינו: מחברים אותו עם דברים וכופלים אותו עם דברים, כולל איתו עצמו. אם אני כופל את \(x\) בעצמו פעם אחת אני מקבל את \(x^{2}\) , אבל אפשר להמשיך עם זה ולקבל את \(x^{3}\) ואת \(x^{4}\) וכן הלאה. פולינום זה משהו שמתקבל אחרי מספר סופי של פעולות כאלו, ולא קשה להשתכנע שהצורה הכללית שלו תהיה

\(a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots+a_{1}x+a_{0}\) כש-\(a_{0},a_{1},\ldots,a_{n}\) הם מספרים שאני מכנה המקדמים של הפולינום (\(a_{k}\) הוא המקדם של החזקה \(x^{k}\) של \(x\) ), ואני גם מוסיף את הדרישה ש-\(a_{n}=0\) , כלומר \(x^{n}\) היא החזקה הכי גבוהה של \(x\) שמופיעה בפולינום הזה. הנתון הזה - מה החזקה הכי גבוהה של \(x\) שמופיעה בפולינום - הוא די חשוב, אז אני נותן לו שם: הדרגה של הפולינום, או המעלה שלו (אלו מילים נרדפות פה). אז למשל \(x^{2}+3x\) שראינו קודם הוא פולינום ממעלה שניה. כשבתיכון לומדים "לפתור משוואות ממעלה שניה"בעצם מה שקורה הוא שנתון פולינום \(p\left(x\right)=ax^{2}+bx+c\) ממעלה שניה, ומחפשים ערכים להציב בו כך שיתקיים \(p\left(x\right)=0\) .

יש בעולם עוד כל מני דברים חוץ מפולינומים, למשל הפונקציה \(f\left(x\right)=2^{x}\) היא לא פולינום, וגם \(f\left(x\right)=\sin x\) וכדומה. מה שמעניין בפולינומים הוא שהם פונקציות פשוטות יחסית - ראינו שהם נבנים רק מפעולות חשבון הבסיסיות של חיבור, חיסור וכפל - אפילו לא חילוק! (אם היינו מרשים חילוק היינו מקבלים אובייקטים כמו \(\frac{1}{1+x}\) שהם מעניינים בפני עצמם אבל הם לא פולינומים והסיפור שלהם מסובך יותר). הפשטות הזו מובילה לכך שבהרבה מקרים כשיש לנו פונקציה מסובכת, או מידע מבולגן, אנחנו שואלים את עצמנו - האם אפשר לתאר את אותו הדבר בעזרת פולינום? אולי אפילו רק בערך?

התשובה למרבה השמחה היא "כן", מתברר שפולינומים הם עניין מועיל בשלל הקשרים. למשל הפונקציה \(f\left(x\right)=\sin x\) שהזכרתי לפני שניה ממודלת לא רע על ידי הפולינום \(x-\frac{x^{3}}{6}+\frac{x^{5}}{120}\) עבור ערכים קרובים לאפס של \(x\) (ועבור ערכים רחוקים מאפס עדיין אפשר להיעזר בפולינום הזה תוך התבססות על כך שסינוס זו פונקציה שחוזרת שוב ושוב על תבנית בסיסית קטנה יחסית - אני מדבר על זה כאן). אפשר ובצדק לשאול מאיפה הפולינום המוזר הזה צץ - זה קשור למשהו שנקרא טורי טיילור ולא אכנס אליו פה אבל יש לי פוסט בנושא. אני רוצה לדבר הפעם על שימוש אחר בפולינומים לצורך קירובים - בפרט עבור המקרה של "מידע מבולגן"שהזכרתי.

הרעיון הוא כזה - נניח שיש לנו אוסף של פרטי מידע של זוגות מספרים. בואו נראה דוגמא עם נתונים שלקחתי מהאינטרנט ואין לי מושג אם הם נכונים - מרחק עצירה:

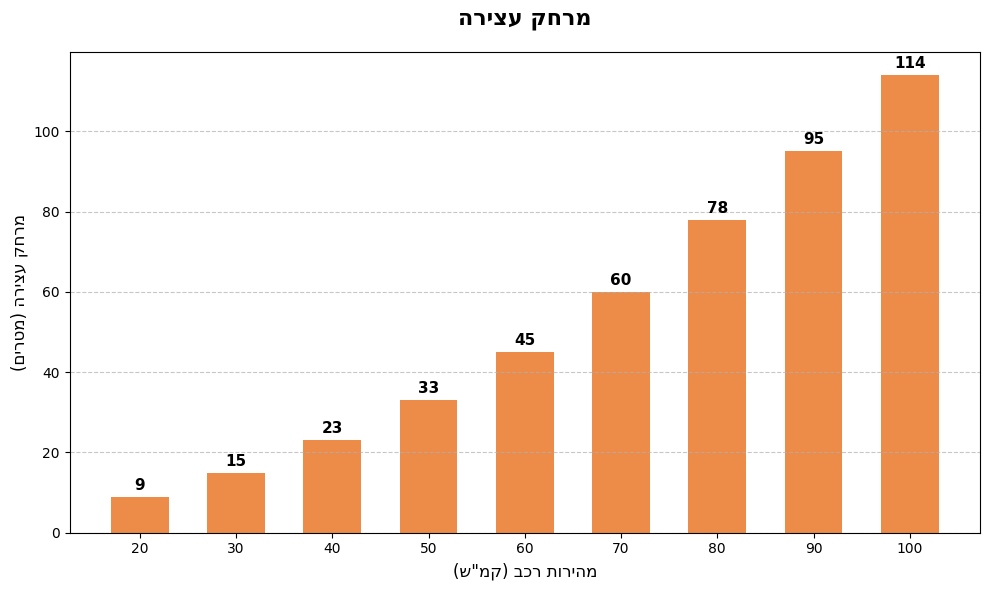
מרחק עצירה הוא המרחק שרכב עובר במקרה של בלימת פתע, החל מהרגע שבו הנהג מזהה את הסכנה שמצריכה בלימת פתע ועד שהרכב עוצר בפועל. זה כולל את המרחק שהרכב עובר בזמן שלוקח לנהג להתחיל לבלום, ואת המרחק שהוא עובר בזמן שהרכב מאט עד לעצירה מוחלטת. מן הסתם המרחק הזה מושפע משלל גורמים, החל במהירות התגובה של הנהג וכלה באיכות הבלמים של הרכב. לכן מלכתחילה הנתון הזה הוא לא איזו אמת מתמטית אבסולוטית שנחתה עלינו משמיים אלא הערכה בלבד, שהדרך הנכונה לאסוף אותה היא לבחון אותה בשטח ולקחת... ממוצע? עזבו, אני אפילו לא בטוח שזו הדרך הנכונה לאמוד אותה. אני כאמור נקטתי בשיטה הלא כל כך אמינה "לגגל באקראי באינטרנט כי אני בסך הכל רוצה מספרים לעבוד איתם".

מבין כל הגורמים שמשפיעים על מרחק העצירה, מה הכי קריטי? שוב, בלי ניסוי מסודר קשה לדעת, אבל די סביר להניח שמהירות הרכב הנוסע תהיה קריטית - רכב שנוסע מהר יותר לוקח יותר זמן לעצור, ובזמן שלוקח לעצור אותו הוא נוסע מרחק גדול יותר. אז הדיאגרמה שלנו מציגה את הזוגות של מהירות ומרחק העצירה שמתאים לה. הזוגות הם:

\(\left(20,8\right),\left(30,15\right),\left(40,23\right),\left(50,33\right),\left(60,45\right),\left(70,60\right),\left(80,78\right),\left(90,95\right),\left(100,114\right)\) הנתונים שלקחתי נותנים את מרחק העצירה עבור מהירויות שמתחלקות ב-10, אבל מה אם אני רוצה לדעת את מרחק העצירה עבור 13? ובכלל, אם אני רוצה לדעת מה הפונקציה שמחזירה לכל מהירות את מרחק העצירה שמתאים לה? ובכן, אף אחד לא אומר שהפונקציה הזו הולכת להיראות נחמד - ככה זה עם מידע "מלוכלך"מהעולם האמיתי. אבל אם אני רוצה פונקציה פשוטה, אני יכול לקבל את זה שהיא בסך הכל תהיה קירוב של הדבר האמיתי, וכל עוד זה קירוב לא רע אני אהיה בסדר עם זה. קירוב כזה נקרא מודל ובסטטיסטיקה אוהבים להגיד "כל המודלים שגויים; חלקם יעילים"כדי שלא נשלה את עצמנו שהמודל הוא-הוא המציאות.

בסטטיסטיקה יש תחום שלם שמוקדש למציאת המודל ה"אופטימלי", כזה שמביא למינימום את השגיאה בין המודל ובין המידע הנצפה, ומודל כזה נקרא רגרסיה וזה תחום מרתק שלא אגיד עליו כלום הפעם כי אני רוצה להסתפק בדיבור על משהו פשוט - אני רוצה למצוא מודל שמתאים בדיוק לחלק מהנתונים, ואני אהיה בסדר עם זה שהוא לא יתאר את היתר בצורה אופטימלית. ואני ארצה שהמודל שלי יהיה פולינום.

הזוג הראשון של קלט/פלט הוא \(\left(20,9\right)\) . הנה פולינום פשוט שעל קלט 20 מחזיר פלט 9: \(p\left(x\right)=9\) . זה... קצת כמו רמאות? פולינום שבכלל לא מתייחס ל-\(x\) ? כן, אבל הוא עובד! אבל בסדר, ברור שהוא לא עובד טוב. למשל, הזוג השני הוא \(\left(30,15\right)\) והפולינום המגוחך שלנו מחזיר 9 גם על הקלט 30 וזה כבר די רחוק מהמספר הנכון. אז אנחנו רוצים פולינום שבו \(x\) כן משתתף. אבל שימו לב רגע למשהו: הזוג \(\left(80,78\right)\) . בזוג הזה הקלט גדול פי 4 מאשר בזוג \(\left(20,9\right)\) אבל הפלט גדול פי 9(בערך). זה רומז לנו שהיחס בין הקלט לפלט הוא לא יחס ישר (מה שפולינום ממעלה ראשונה מתאר) אלא יותר מזה - אז מה שמעניין אותי הוא למצוא פולינום ממעלה שניה שמתאים לנתונים. איך נעשה את זה? וכמה פולינומים כאלו יש? כאן אני רוצה לגלוש טיפה לתיאוריה.

הנה הטענה התיאורטית המרכזית: אם יש לי סדרה של \(d+1\) זוגות, \(\left(x_{0},y_{0}\right),\ldots,\left(x_{d},y_{d}\right)\) אז קיים פולינום יחיד \(p\left(x\right)\) ממעלה לכל היותר \(d\) כך ש-\(p\left(x_{i}\right)=y_{i}\) לכל \(0\le i\le d\) .

מכירות את הקטע הזה של "דרך כל שתי נקודות עובר קו ישר יחיד"? זה בדיוק זה - קו ישר הוא פונקציה שאפשר לתאר על ידי פולינום ממעלה ראשונה, ושני נקודות הן שני זוגות \(\left(x,y\right)\) של מספרים. אז שתי נקודות קובעות חד משמעית קו ישר, ושלוש נקודות יקבעו חד משמעית פרבולה/מעגל (אלו אובייקטים שמתוארים על ידי משוואה ממעלה שניה, אם כי בצורה טיפה יותר מסובכת מאשר סתם פולינום אבל זה מגיע מאותו מקום) וכן הלאה. אני קודם רוצה להסביר למה הפולינום הזה הוא יחיד ואז נגיע לאקשן האמיתי - איך למצוא אותו.

היחידות נובעת מטענה יותר בסיסית על פולינומים: לפולינום ממעלה \(d\) יש לכל היותר \(d\) שורשים - כש"שורש"הוא מספר שמציבים בפולינום ומחזיר 0. בהינתן הטענה הזו, הטענה על היחידות די קלה. נניח שיש לנו שני פולינומים \(p\left(x\right),q\left(x\right)\) ממעלה לכל היותר \(d\) כך ששניהם מקיימים \(p\left(x_{i}\right)=y_{i}=q\left(x_{i}\right)\) לכל \(1\le i\le d\) . עכשיו, בואו נסתכל על ההפרש שלהם, \(a\left(x\right)=p\left(x\right)-q\left(x\right)\) . גם ההפרש הוא פולינום ממעלה לכל היותר \(d\) , אבל הוא מקיים \(a\left(x_{i}\right)=p\left(x_{i}\right)-q\left(x_{i}\right)=0\) לכל \(0\le x_{i}\le d\) , כלומר יש לו \(d+1\) שורשים שונים(אני מניח שכל ה-\(x\) -ים שונים אחד מהשני כי אם אותו \(x\) מופיע פעמיים זה חייב להיות עם אותו \(y\) כי הרי זו פונקציה, אבל אז סתם שכפלתי מידע קיים ולא הוספתי מידע חדש). לכאורה הגענו לסתירה, אבל יש חריג אחד למשפט שאמרתי קודם - אם הפולינום הוא פולינום האפס, כלומר הפולינום \(a\left(x\right)=0\) , אז מן הסתם יש לו אינסוף שורשים - לכן לפעמים מגדירים את הדרגה שלו בתור \(\infty\) במקום 0 כמו שנראה שזה אמור להיות. אבל אם \(p\left(x\right)-q\left(x\right)=a\left(x\right)=0\) אז \(p\left(x\right)=q\left(x\right)\) לכל נקודה, מה שמראה את היחידות.

אם אני כבר בשוונג - למה המשפט על "לכל היותר \(d\) שורשים"הוא נכון? זו כבר טיפה סטייה מהנושא אבל למה לא. בבסיס העניין נמצאת העובדה שאפשר לחלק פולינומים: אם יש לנו \(a\left(x\right),b\left(x\right)\) אז קיימים \(q\left(x\right),r\left(x\right)\) כך ש-\(a\left(x\right)=q\left(x\right)b\left(x\right)+r\left(x\right)\) כך שדרגת \(r\) קטנה ממש מדרגת \(q\) (או ש-\(r\) הוא פולינום האפס).

עכשיו, אם \(p\left(x\right)\) הוא פולינום ו-\(\alpha\) הוא שורש שלו, כלומר \(p\left(\alpha\right)=0\) , אז בואו נחלק את \(p\) בפולינום ממעלה ראשונה \(x-\alpha\) : נקבל שיש \(q\left(x\right)\) ו-\(r\left(x\right)\) כך ש-\(p\left(x\right)=q\left(x\right)\left(x-\alpha\right)+r\left(x\right)\) . אם נציב עכשיו \(x=\alpha\) אז נקבל:

\(0=p\left(\alpha\right)=q\left(\alpha\right)\left(\alpha-\alpha\right)r\left(\alpha\right)=r\left(\alpha\right)\) העניין הוא ש-\(r\) הוא ממעלה קטנה מ-\(x-\alpha\) , כלומר הוא ממעלה 0 או שהוא פולינום האפס. אבל אם הוא ממעלה 0, כלומר קבוע, והוא שווה ל-\(0\) כש"מציבים"בו \(\alpha\) הוא חייב להיות קבוע 0. המסקנה היא ש-\(\left(x-\alpha\right)\) מחלק את \(p\left(x\right)\) ללא שארית, עבור כל שורש \(\alpha\) של \(p\left(x\right)\) . כלומר, \(p\left(x\right)=q\left(x\right)\left(x-\alpha\right)\) - כאן \(q\) הוא ה"מנה"של החלוקה. שימו לב שכל שורש של \(p\) ששונה מ-\(\alpha\) יהיה גם שורש של \(q\) .

עכשיו אפשר להוכיח את הטענה על מספר השורשים באינדוקציה: לפולינום ממעלה 1 בבירור יש רק שורש אחד (כי פולינום כללי ממעלה \(1\) הוא מהצורה \(ax+b\) כאשר \(a\ne0\) וזה מתאפס אך ורק עבור \(x=-\frac{b}{a}\) ). נניח שלפולינום ממעלה \(d\) יש לכל היותר \(d\) שורשים, אז עבור פולינום ממעלה \(d+1\) , אם קיים לו שורש \(\alpha\) אז נחלק אותו ב-\(x-\alpha\) , נקבל פולינום ממעלה \(d\) , נפעיל עליו את הנחת האינדוקציה - יש לו לכל היותר \(d\) שורשים. נצרף אליהם את \(\alpha\) וקיבלנו של-\(p\) יש לכל היותר \(d+1\) שורשים, וסיימנו.

כמובן, עדיין לא הוכחתי את הטענה על חלוקת פולינומים, אבל נראה לי שאעצור כאן - רק שימו לב שהטענה הזו לא נכונה באופן כללי; זה תלוי איפה הפולינומים "חיים". אצלנו אני מניח במובלע שהפולינומים הם עם מקדמים ממשיים, אבל בסיטואציות יותר מורכבות (פולינומים מעל שדות סופיים למשל) לא בהכרח מתקיימת תכונת החלוקה היפה שדיברתי עליה ולפולינום ממעלה \(d\) יכולים להיות יותר מ-\(d\) שורשים (דוגמא קלאסית למי שמכירות: מעל \(\mathbb{Z}_{8}\) לפולינום \(x^{2}-1\) יש ארבעה שורשים).

חזרה אלינו - הראיתי שאם יש פולינום אינטרפולציה של \(d+1\) נקודות אז הוא יחיד (מבין כל הפולינומים ממעלה עד וכולל \(d\) ). אבל איך מוצאים אותו? יש לכך כמה דרכים, ואני אראה את הדרך הנפוצה - אינטרפולציית לגראנז'. אני יכול כמובן פשוט להפיל עלינו את הנוסחה ה"מפחידה", לתת לכולנו להיבהל ואז להסביר מה הולך שם - אבל אני לא אוהב את הגישה הזו, אני מעדיף להראות בדיוק מאיפה הנוסחה הזו מגיעה לפני שמציגים אותה בשלמותה. ולמרבה המזל, הרעיון הבסיסי שמאחוריה הוא פשוט מאוד.

בואו נחזור על מה שיש לנו - אוסף של \(d+1\) זוגות קלט/פלט: \(\left(x_{0},y_{0}\right),\ldots,\left(x_{d},y_{d}\right)\) . אני רוצה לבנות פולינום \(p\left(x\right)\) שמקיים \(p\left(x_{i}\right)=y_{i}\) עבור \(0\le i\le d\) . עכשיו, בואו נניח שהצלחתי למצוא בדרך פלא פולינום \(p_{i}\) שהוא בעל התכונה המופלאה הבאה: על \(x_{i}\) הוא מחזיר את \(y_{i}\) ועל כל \(x_{j}\) אחר מבין הקלטים הוא מחזיר 0. כלומר

\(p_{i}\left(x_{j}\right)=\begin{cases} y_{i} & j=i\\ 0 & j\ne i \end{cases}\)

אם מצאתי \(p_{i}\) כזה לכל \(0\le i\le d\) , סיימתי! אני אגדיר \(p\left(x\right)=p_{0}\left(x\right)+p_{1}\left(x\right)+\ldots+p_{d}\left(x\right)\) , ועכשיו כשאני מציב \(x_{i}\) ב-\(p\) , כל המחוברים מתאפסים חוץ מ-\(p_{i}\left(x_{i}\right)=y_{i}\) .

אז המטרה שלי עכשיו היא להבין איך לממש את \(p_{i}\) . אבל לפני כן, בואו נציב לעצמנו מטרה קצת יותר צנועה - לבנות פולינום שמתאפס על כל \(x_{j}\) עבורו \(j\ne i\) , ולא חשוב כרגע מה הוא מחזיר על \(x_{i}\) . האם אנחנו יודעים לבנות פולינום כזה? ובכן, כן! ראינו את זה לפני רגע למעשה. ראינו שאם \(\alpha\) מאפס פולינום כלשהו, הפולינום חייב להתחלק ב-\(x-\alpha\) , ולכן פולינום שמתאפס על כל \(x_{j}\) כך ש-\(j\ne i\) חייב להתחלק בכל ה-\(x-x_{j}\) -ים הללו. אז בואו פשוט נכפול את כולם:

\(p_{i}\left(x\right)=\left(x-x_{0}\right)\left(x-x_{1}\right)\ldots\left(x-x_{i-1}\right)\left(x-x_{i+1}\right)\ldots\left(x-x_{d}\right)\)

אוקיי הצילו, זה כתיב מסורבל מדי. בואו נכניס את הכתיב המקובל לכפל מקוצר:

\(p_{i}\left(x\right)=\prod_{j\ne j}\left(x-x_{j}\right)\)

הבעיה עם הפולינום הזה היא שכשמציבים בו \(x_{i}\) , לא מקבלים את \(y_{i}\) . מקבלים איזה שהוא ערך שהוא עיסת מישמש לא ברורה:

\(p_{i}\left(x_{i}\right)=\prod_{j\ne j}\left(x_{i}-x_{j}\right)\)

אין לי מושג מה המספר הזה, אני רק יודע שהוא לא 0, כי \(x_{i}-x_{j}\ne0\) לכל \(i\ne j\) . ואם המספר הזה הוא לא 0 אז אפשר לחלק בו. אז בואו נגדיר מחדש את \(p_{i}\) :

\(p_{i}\left(x\right)=\prod_{i\ne j}\frac{x-x_{j}}{x_{i}-x_{j}}\)

הפולינום הזה הוא בעל תכונה מאוד נחמדה:

\(p_{i}\left(x_{j}\right)=\begin{cases} 1 & j=i\\ 0 & j\ne i \end{cases}\)

מה שעשיתי כאן נקרא לנרמל - היה לי משהו שהגודל שלו הוא לא 1, אז חילקתי אותו בגודל שלו והופס, קיבלתי משהו מגודל 1. זה מעולה, אבל אני הרי רציתי שהפולינום יחזיר \(y_{i}\) . למרבה המזל, מרגע שנירמלתי אני פשוט יכול לכפול את הכל ב-\(y_{i}\) , כלומר להגיע להגדרה הסופית של \(p_{i}\) :

\(p_{i}\left(x\right)=\prod_{i\ne j}\frac{x-x_{j}}{x_{i}-x_{j}}y_{i}\)

ועכשיו אפשר להשתמש בסימון המקוצר לחיבור, ולקבל את פולינום האינטרפולציה:

\(p\left(x\right)=\sum_{i=0}^{d}\prod_{i\ne j}\frac{x-x_{j}}{x_{i}-x_{j}}y_{i}\)

הפולינום הזה עובד. שימו לב לכך שהוא ממעלה \(d\) , כי במכפלה \(\prod_{i\ne j}\frac{x-x_{j}}{x_{i}-x_{j}}\) משתתפים רק \(d\) מוכפלים, כל אחד מהם תורם 1 לחזקה של \(x\) . סיימנו! זו הנוסחה המפחידה שדיברתי עליה!

עכשיו אפשר לחזור אל הנתונים הגולמיים שראינו קודם. אם נלך לנתוני מרחק העצירה, ונבצע אינטרפולציה על הנקודות \(\left(20,9\right),\left(30,15\right),\left(40,23\right)\) נקבל את הפולינום \(\frac{x^{2}}{100}+\frac{x}{10}+3\) ובאמת אם ננסה להציב בו \(20,30,40\) נקבל \(9,15,23\) בהתאמה. קסם! אבל מה עם יתר הערכים שיש לנו? אם נציב 50 נקבל 33 ואם נציב 60 נקבל 45, בדיוק כמו בנתונים שלנו! אבל... אם נציב 70 נקבל 59, לא 60. כאן המודל שלנו כבר חורג מהתוצאות הנצפות בפועל.

כמובן, אפשר לנסות לבצע אינטרפולציה חדשה שכוללת את אותן הנקודות \(\left(20,9\right),\left(30,15\right),\left(40,23\right)\) מקודם ובנוסף לכך את הנקודה החדשה \(\left(70,60\right)\) . התוצאה תהיה פולינום ממעלה שלוש שנראה די מפחיד:

\(\frac{x^{3}}{6000}+\frac{17x^{2}}{2000}+\frac{43x}{300}+\frac{13}{5}\) הפולינום הזה תואם את כל הנקודות שהזנתי לאינטרפולציה, אבל הוא מזייף בנקודות אחרות. למשל, עבור \(80\) הוא יחזיר 77 ולא 78. אבל גרוע מכך, על 50 הוא יחזיר \(\frac{331}{10}=33.1\) , לא 33 - איבדנו תוצאה שקיבלנו קודם "במזל"(כי היא הייתה על ערך שלא השתתף באינטרפולציה). אני חושב שהרעיון ברור - אינטרפולציה במובן שהצגתי כאן נותנת התאמה מדויקת לערכים שהזנתי לה, במחיר של ויתור על כל יתר הערכים שלא הזנתי. לכן השיטה הזו היא רק תחילת הסיפור, לא סופו. אבל זו התחלה יפה!

בואו נחזור עכשיו לחידה מתחילת הפוסט:

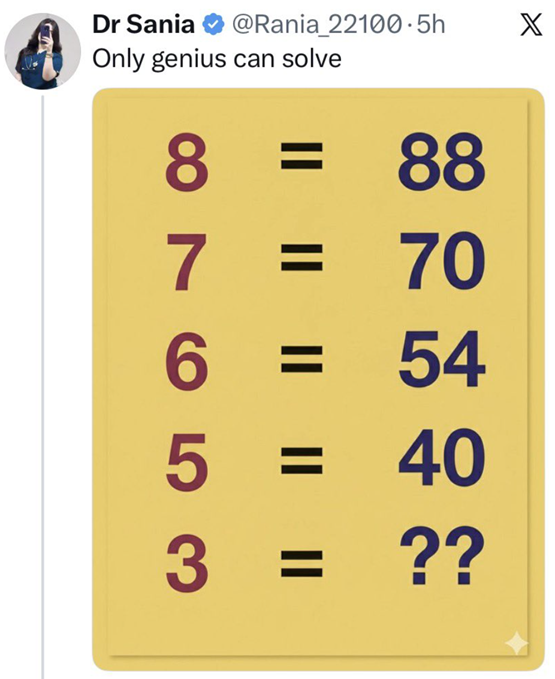
מה שיש לנו פה הוא את סדרת הנקודות \(\left(8,88\right),\left(7,70\right),\left(6,54\right),\left(5,40\right)\) . להזין את זה לנוסחת האינטרפולציה יניב באופן לא מפתיע את הפולינום \(x^{2}+3x\) שהצבה של 3 בו מחזירה 18. האם זה אומר ש-18 הוא אכן הפתרון לחידה? רק אם אנחנו בוחרים להניח שהחידה שואלת משהו בסגנון "אם מוצאים פונקציה פשוטה ביותר שמייצגת את הקשר שמעביר את הקלטים באגף שמאל לפלטים באף ימין ומציבים בה את הערך התחתון ביותר באגף שמאל מה נקבל?" ומוסיפים על זה את ההנחה ש"פשוטה ביותר" זה "פולינומית ממעלה מינימלית". אז כן, אפשר להניח את כל ההנחות הללו, אבל... במקרה הזה, מה בעצם נשאר מהחידה? כמו שאנחנו רואים, אין כאן חשיבה, יש אלגוריתם אינטרפולציה כללי שפשוט צריך להפעיל אותו פה. מה הכיף כאן? אוקיי, ומה עם החידה השניה שהצגתי?

כאן אינטרפולציה של ארבעת הזוגות הראשונים תניב את הפולינום \(p\left(x\right)=-32335x^{3}+392510x^{2}-950185x+591010\) שאיך נגיד, לא מעורר תחושות פשוטות במיוחד. להציב בו \(x=5\) ייתן \(1610960\) שהוא... מספר... כלשהו? מה הקטע פה? ובכן הקטע כמובן הוא שסדרת המספרים הזו לא הגיעה משום פולינום או משום דבר מתמטי כלשהו אלא מהראש המאוד כאוטי של דני סנדרסון - ההתאמה פה היא "\(n\) עובר למספר שאותו שרים בשורה ה-\(n\) בבית האחרון של השיר 'אלף כבאים'":

אלף כבאים, לא יצליחו לכבות

אלפיים צבעים, לא יצליחו לכבות

ארבע מאות אלף פרשים, לא יצליחו לכבות

מיליון ותשע מאות תשעים, לא יצליחו לכבות

אלף כבאים, לא יצליחו לכבות אותי

אז התשובה היא 1,000. סליחה, פולינומים, מתברר שפשוט יש דברים שאתם לא מתאימים להם.