מה בין טופולוגיה, First-person shooters, נמלים שמטיילות על טבעות ובקבוקים בלתי אפשריים?

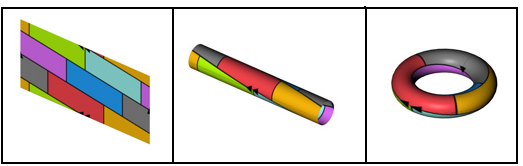
בפוסטים הקודמים עסקתי בטופולוגיה קבוצתית והצגתי בנייה מסובכת למדי - בנייה של מרחב באמצעות “מכפלה” של מרחבים קטנים יותר. למשל, אפשר ליצור מלבן על ידי “הכפלה” של שני קווים. כעת אני רוצה לעסוק בבנייה אחרת, חשובה לא פחות - “הדבקה”. לפני שאציג אותה בצורה פורמלית, הנה הרעיון הכללי: הדבקה היא התהליך שבו אנו מסוגלים להפוך מלבן לטבעת. הרעיון הבסיסי שבהדבקה הוא לקחת שני חלקים מהמרחב שלנו, לשים אותם זה על זה, “למרוח דבק” ולחבר אותם, כך שאנו “שוכחים” שהיו במקור שני קצוות ששמנו אחד על השני - מקום החיבור נראה לנו כמו יחידה רציפה אחת. דוגמה דו ממדית פשוטה לכך היא זו: ניקח קו ישר. נתפוס את שני קצותיו. נמשוך אותם כלפי מעלה עד אשר הם יגעו זה בזה, ואחר “נדביק” אותם. קיבלנו מעגל. כלומר, ניתן לבנות מעגל מקו באמצעות הדבקה.

איך עושים את זה באופן פורמלי? באמצעות המושג של יחס שקילות. יחס שקילות, שכבר תיארתי בעבר, הוא דרך מתמטית להגיד “מעכשיו, בכל ההיבטים שמעניינים אותי, שני האיברים הבאים הם אותו דבר”. במקרה של הקו שהופך למעגל, הדרך הפורמלית להגדיר זאת היא כך: אם הקו שלנו הוא \( [0,1] \), אז נגדיר יחס שקילות לפיו 0 שקול ל-1, ואילו \( x \) שקול רק לעצמו, לכל נקודה \( 0<x<1 \). התוצאה? הפכנו את 0 ו-1 ל”אותו הדבר”, ואילו את שאר הנקודות במרחב לא שינינו.

דרך טובה לחשוב על הסיטואציה הזו היא מנקודת מבטה של נמלה שהולכת “בתוך” הקו: היא מתחילה מהנקודה 0, הולכת הולכת הולכת ימינה, מגיעה ל-1, ואז שום דבר לא עוצר אותה - הרי 1 זהה ל-0, ולכן הגעה ל-1 כמוה כחזרה ל-0, ולכן היא מסוגלת להמשיך ללכת עוד ועוד ועוד ימינה, בלי לעצור לעולם, אבל כאשר היא כל הזמן חולפת על פני נקודות שהיא כבר ראתה בעבר. לדבר כזה יש שם “להסתובב במעגלים”, והוא נכון גם אם הצורה שבה אנחנו הולכים איננה מעגל מושלם. זו נקודה שממחישה יפה את מה שהטופולוגיה עוסקת בו - מבחינה טופולוגית, אין הבדל מהותי בין מעגל וריבוע - אפשר “למתוח” ריבוע עד שהוא יראה כמו עיגול יפה.

איך זה קשור למשחקי מחשב?

אחת מההצלחות המפתיעות יחסית של שנת 2007 היא המשחק Portal. המשחק פותח על ידי החברה שיצרה את סדרת Half-Life - סדרה של משחקי יריות מגוף ראשון ששמה נודע לתהילה, והוא משתמש באותו מנוע שעליו מבוסס Half-Life 2. המשחק ההוא התהדר בעולם דינמי יחסית, שבו ניתן להזיז רבים מהחפצים שנראים על המסך, והדבר היה בסיס לאחד מכלי הנשק המקוריים ביותר במשחקי מחשב - ה-Gravity Gun, כלי נשק שמסוגל למשוך חפצים מרחוק, ואחר כך להשליך אותם בעוצמה (או סתם להניח אותם בשקט). כתוצאה מכך, הסביבה כולה הופכת לכלי נשק פוטנציאלי אחד גדול (ויש עוד דברים משעשעים שניתן לעשות עם הרובה - לא ניכנס לכך כרגע).

עם כל מעלותיה, Half-Life היא בסופו של דבר סדרת משחקי יריות - אתה הולך, באים אויבים ומנסים להרוג אותך, אתה מפוצץ להם את הצורה. פה ושם יש פאזל כלשהו - מכשול שלא ברור איך עוברים וצריך קצת לחשוב - אבל עדיין, השורה התחתונה היא “יש לך כלי נשק - תפצפץ איתם לאויבים את הצורה”. זה גם השימוש המקובל ביותר למנועי תלת-מימד שבהם משתמשים למשחקים שבהם נקודת המבט היא First-person (שימוש נפוץ אחר הוא במשחקי תפקידים ממוחשבים, למשל Oblivion).

לכן Portal הוא חריג יחסית בנוף של ימינו - הוא משחק פאזלים “טהור” יחסית. עיקר האתגר בו אינו לחמוק מאויבים ולירות עליהם בחזרה, אלא לנסות ולפתור חידות שונות ומשונות, שסובבות כולן סביב ה”נשק” היחיד שיש לך - ה-Portal Gun, רובה הפורטלים.

הרעיון שמאחורי הרובה הוא פשוט עד כדי גיחוך - כשיריה מהרובה פוגעת בקיר, נפתח פורטל - שער - בתוך הקיר. יש שני סוגי שערים אפשריים - שער כתום, ושער כחול (אתה שולט על איזה צבע אתה רוצה לירות). בכל פעם שבה אתה פותח פורטל כחול, נסגר הפורטל הכחול הדומה, וכך גם עם הכתום. הפואנטה: אם נכנסים לפורטל הכחול יוצאים דרך הפורטל הכתום, ולהיפך. זה הכל.

על בסיס העיקרון הפשוט הזה ניתן להמציא פאזלים מכאן ועד להודעה חדשה. כמובן שהחיים הם מאוד מסובכים - לא על כל הקירות אפשר לפתוח פורטלים, וכדי לעבור מאיזור לאיזור צריך ללחוץ על כפתורים ולגרור עליהם תיבות ולהתחמק מזקיפים שמנסים לירות בך, וכדומה; אבל הדרך להתגבר על כל האתגרים היא באמצעות מחשבה, כשזריזות הידיים (שנדרשת לפעמים, ואינה רבה) היא רק האמצעי להוציא לפועל את התוכנית המדוקדקת שחשבת עליה.

ההמחשה הנפוצה ביותר לאופן החשיבה השונה שהפורטלים מספקים היא בדרך שהם מציעים לקפוץ מעל תהומות; במשחקים אחרים כנראה שהיינו פשוט רצים ומקווים שהתנופה תספיק לנו. לא בפורטל. בפורטל, פותחים על הקיר מאחוריך שער כתום שפונה אל עבר התהום, מזנקים לתוכה, צוברים מהירות ואז יורים פורטל כחול על הרצפה, במקום שבו אתה עומד לפגוע. התוצאה? אתה מתעופף במהירות דרך השער הכתום שפתחת קודם, בכיוון תנועה שהפך מאנכי לאופקי בן רגע, ועובר את התהום.

כל מי שרוצה להתרשם מהרעיונות הבסיסיים של המשחק יכול לנסות את גרסת הפלאש שלו. מדובר במשחק עצמאי, שלא פותח על ידי אותה חברה, והוא דו ממדי, מבוסס רשת, וגם כן מהנה למדי.

ומה כל זה קשור לטופולוגיה? ובכן, הפורטלים הם בסך הכל המחשה פשוטה לרעיון ה”הדבקה”. הביטו לרגע בתמונה שלעיל ובשני הפורטלים שבה; בדרך כלל כדי להמחיש את רעיון “הרצפה מודבקת לקיר” היינו צריכים לדמיין כיצד יד ענקים תופסת את הרצפה, “מותחת אותה” במעין חצי מעגל עם כיוון השעון עד שהיא נצמדת אל הקיר מאחורה; מהמראה המקורי של החדר לא היה נותר כלום. העיוות הזה אולי בלתי מורגש מבחינה טופולוגית, אבל הוא עשוי להקשות על ההבנה של “איך העולם נראה” אחרי שמבצעים אותו. לעומת זאת, הפורטלים נותנים אינטואיציה שונה. העולם לא השתנה; שום דבר לא זז. מה שכן קרה הוא שנפתחה דרך חדשה, “קסומה”, שמובילה מהרצפה אל הקיר באפס זמן. שני מקומות שלפני רגע היו מרוחקים הפכו לקרובים מאוד, ל”דבוקים”.

הבה ונציג עוד כמה דוגמאות להדבקות, מהסוג שאפשר לעשות בבית גם בלי רובה פורטלים. נתחיל בדוגמה פשוטה ונאה - הטורוס. טורוס הוא פשוט בייגלה - טבעת תלת ממדית. את הברנש הזה ניתן ליצור ממלבן על ידי שתי הדבקות. קחו מלבן והדביקו את שפתו העליונה לשפתו התחתונה. התוצאה היא גליל חלול. כעת קחו את שני קצוות הגליל והדביקו אותם זה לזה (קצת קשה לעשות את זה עם דף נייר) - התוצאה היא הבייגלה.

הצגתי את הטורוס בתור תוצר של שתי הדבקות; למעשה, אפשר להציג אותו גם באמצעות פעולת ההכפלה - הוא מכפלה של שני מעגלים. הטענה הזו עשויה להישמע מוזר למדי בהתחלה, אבל לא קשה לדמיין אותה: נניח שיש לכם חישוק (מעגל מס’ 1) ואתם משחילים עליו CD (שהוא עיגול עם חור באמצע, אבל נניח שזה מעגל), ואתם מוסיפים עוד ועוד CD-ים עד שאין מקום על החישוק - מה שתקבלו ייראה כמו טורוס, ומה שביצעתם הוא בדיוק הכפלה (בכל נקודה אפשרית על המעגל הראשון - החישוק - השחלתם מעגל שני - ה-CD).

הקשר הזה (הטורוס הוא גם תוצר של הדבקות וגם של מכפלות) אינו מקרי, כמובן; מעגל הוא תוצר של הדבקה של קו, ומלבן הוא תוצר של מכפלת שני קווים. לכן הטורוס מתקבל בכל מקרה מהאובייקט היסודי “קו” באמצעות שתי הדבקות והכפלה אחת - או שקודם כל נדביק כל קו עם עצמו ונקבל שני מעגלים, ואז נכפיל אותם ונקבל טורוס; או שקודם כל נכפיל את הקווים ונקבל מלבן, ואז נבצע עליו שתי הדבקות ונקבל טורוס.

המחשה לפעולת ההדבקה ניתן לקבל בתרשים הבא:

התרשים אמור להציג מלבן, כשבמקום צלעות מוצגים חצים. החצים מרמזים על כך שאנחנו עומדים להדביק את הצלעות; הרעיון הוא ששתי צלעות שאנו מדביקים זו על זו צריכות להיות מודבקות כאשר החץ מצביע לאותו כיוון. אם תחשבו על הצורה שבה המלבן מקופל לטורוס, זה אכן מה שקורה. אם כך, מדוע התרשים מעניין? כי אפשר להשתמש באותו סימון כדי להבהיר בניות ברורות פחות.

כעת אפשר לנסות ולהציג שני אובייקטים מופרעים הרבה יותר - האחד, טבעת מביוס, פשוט ביותר לבניה וכל אחד יכול ליצור אותו בבית; השני, בקבוק קליין, לא ממש יכול להתקיים במציאות. נתחיל מטבעת מביוס: הרעיון הוא לקחת מלבן ולבצע הדבקה אחת של שתי צלעות מנוגדות, אולם במקום ההדבקה ה”רגילה” (שראינו שמובילה לגליל - או, במקרה שבו המלבן מאוד ארוך וצר ואנחנו מדביקים את שתי הצלעות הקצרות, למשהו שנראה כמו טבעת דו ממדית, אבל מבחינה פורמלית הוא עדיין גליל) אנחנו עושים “טוויסט” בצלעות לפני שאנחנו מדביקים אותן:

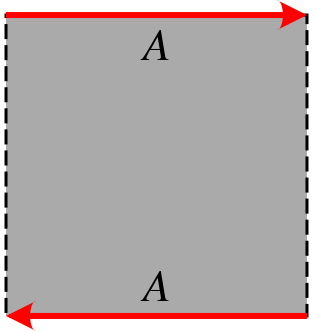
מה שקורה כאן הוא פשוט מאוד - חשבו כיצד ניתן להדביק את שתי הצלעות האדומות זו על זו כך שכיווני החצים בהן (ברגע ההדבקה) יהיה זהה - חייבים לפתל את הנייר כדי להפוך את כיוון החץ באחת מהצלעות. האובייקט שמתקבל נראה כך:

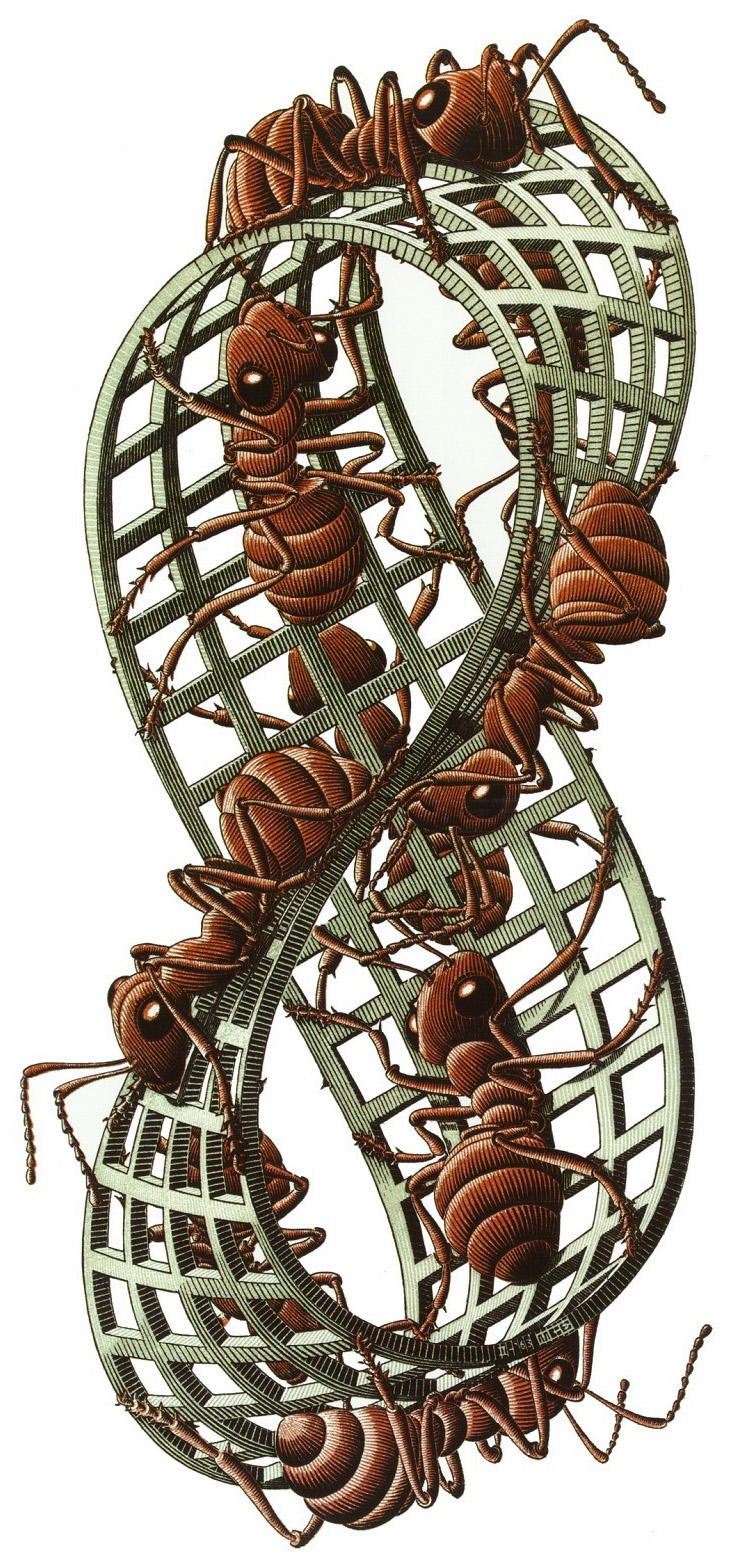
המעניין בו, מבחינה מתמטית, הוא העובדה שמדובר במשטח שלא ניתן לכוון, כלומר אין בו “צד עליון” ו”צד תחתון”. בטבעת רגילה, למשל, היינו מקבלים את הצד שפונה “פנימה” (עוטף את האצבע) והצד שפונה “החוצה” גלוי כלפי חוץ). אם בטבעת רגילה היינו מתחילים לטייל על גבי הצד החיצוני, היינו מסתובבים עליו שוב ושוב לנצח, ולעולם לא היינו מגיעים בטעות לצד הפנימי. לעומת זאת, בטבעת מביוס אין זה משנה איפה נתחיל לטייל - בסופו של דבר נעבור על “שני” חלקי הטבעת. טופולוגים אוהבים לתאר את הטיול הזה באמצעות מה שרואה נמלה (שעולמה צר), וזה כנראה הבסיס לציור המפורסם של אשר על הנמלים שמטיילות על גבי טבעת מביוס:

(או שמא בגלל אשר הטופולוגים אוהבים להשתמש בנמלים?)

כעת לבקבוק קליין. הדיאגרמה של בקבוק קליין אינה מסובכת במיוחד - היא מזכירה מעין שילוב של דיאגרמת הטורוס ודיאגרמת טבעת מביוס (כל התמונות באדיבות ויקיפדיה האנגלית):

מה הולך כאן? קודם כל נדביק את שתי הצלעות האדומות זו לזו. נקבל גליל:

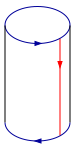
כעת צריך להדביק את שני קצות הגליל, אבל אי אפשר לעשות זאת בשיטה הרגילה, שיוצרת טורוס; החצים לא יתאימו (נסו לדמיין איך זה ייראה). מה שצריך לעשות הוא ליצור מהגליל מעין צורת פרסה:

כעת נתפוס את הקצה הנמוך יותר של הפרסה ונכניס אותו בכוח לתוך הצוואר השני של הפרסה:

כעת אפשר להדביק את שני הקצוות (שהאחד נמצא בתוך השני) זה אל זה. התוצאה נראית בערך כך:

הדבר הזה נקרא “בקבוק קליין” שכן אפשר לדמיין את התהליך כולו עבור בקבוק, שהוא בסך הכל יצור דמוי גליל (מבחינה טופולוגית) - לוקחים את הפיה של הבקבוק, דוחפים אותה מהצד אל תוך הבקבוק, ומדביקים לתחתית (בתחתית יש חור כדי שהבקבוק באמת יהיה גליל).

היצור הזה הוא אנלוגיה תלת ממדית של טבעת מביוס הדו ממדית במובן זה שגם הוא לא ניתן לכיוון: אם תתחילו לטייל כשאתם על הבקבוק, אתם עשויים להגיע לכל נקודה על פני המשטח (חשבו לרגע איך אם התחלתם מבחוץ תוכלו להגיע “פנימה”) אם כן, מה הבעיה בבניה הזו? למה הבקבוק לא יכול להתקיים במציאות? כי החלק של “להכניס את צוואר הבקבוק לתוכו” לא ניתן למימוש מעשי בלי לפעור בגוף הבקבוק חור ולגרום לו לחתוך את עצמו. בקבוק קליין המתמטי לא כולל חיתוך שכזה, ולכן הצורה התלת ממדית שאנו כן מסוגלים ליצור (ולדמיין) איננה בדיוק בקבוק קליין המתמטי. כיצד כן ניתן ליצור את בקבוק קליין, אם כן? נניח שהיינו במרחב בעל ארבעה ממדים ולא שלושה (כן, כן, “הזמן הוא מימד” - עזבו אתכם מזה רגע) - אפשר היה את השלב של “צוואר הבקבוק נכנס פנימה” לבצע באמצעותו מבלי לחתוך את הבקבוק. קשה מאוד לדמיין את זה, אבל למרבה המזל, אפשר לנצל את המרחב התלת ממדי כדי לתת אנלוגיה.

נניח שיש לנו כביש מהיר (כביש הוא אובייקט דו ממדי - אפשר לחשוב עליו כעל מלבן ארוך), ואנו סוללים כביש חדש, שצריך לחצות אותו היכן שהוא. מה נעשה? דרך אחת היא לגרום לשני הכבישים להיחתך, אבל זו דרך גרועה כי איננו רוצים לחתוך כביש מהיר. הדרך השנייה היא לבנות גשר מעל הכביש המהיר - לקחת את האובייקט הדו ממדי של הכביש שאנו בונים, ו”להזיז” אותו בתוך המרחב השלישי, שעד כה טרם ניצלנו - הגובה. אם קטע הכביש שלנו שעובר באותן קוארדינטות במישור של הכביש המהיר יעשה זאת כאשר הקוארדינטה השלישית שלו (הגובה) שונה, לא יווצר חיתוך. הרעיון הזה נשמע ממש טריוויאלי כשמדמיינים אותו בתלת מימד; כל מה שצריך לעשות הוא לדמיין אותו בארבעה ממדים. מתמטיקאים מתארים ללא שום קושי מרחבים בעלי כל מספר סופי של ממדים שרק נרצה - לכל נקודה במרחב בעל n ממדים, פשוט מתאימים n ערכים מספריים של מיקום הקוארדינטה בכל אחד מהממדים. אם כן, מבחינתם כל מה שקורה כאשר “מגביהים” את צוואר הבקבוק בתוך המימד הרביעי הוא שהקוארדינטה הרביעית משנה את ערכה המספרי, ושאר הקוארדינטות לא. אחר כך, כאשר “מזיזים” את צוואר הבקבוק אל תוך הבקבוק יהיה רגע שבו כל שלוש הקוארדינטות הראשונות של צוואר הבקבוק יהיו זהות לקוארדינטות של גוף הבקבוק, כלומר לכאורה אמור להיווצר חיתוך; אלא שהקוארדינטה הרביעית תהיה שונה, ולכן לא יווצר חיתוך וכולם יהיו מרוצים.

לרוע המזל, קשה לדמיין את זה בעיניים, כי אי אפשר לדמיין בקבוק שזז במישור הרביעי מבלי לזוז בכלל באף מישור אחר; לכן צריך להסתפק בתמונת הגשר התלת ממדית, ולהגיד “זה אותו הדבר בדיוק גם בבקבוק”.

מי יודע, אולי בקרוב ייצא משחק מחשב שיספק אינטואיציה טובה יותר גם לגבי זה?