איך אוילר עוזר לנו לבנות בתים ולטייל על גשרים

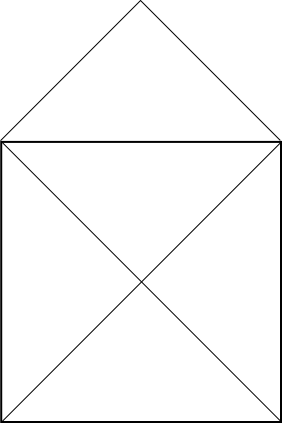
שעשוע ידוע שנהוג לתת לילדים הוא זה:

האתגר כאן פשוט - האם ניתן לצייר את ה”בית” מבלי להרים את העפרון מהדף, כלומר בקו אחד. התשובה חיובית - נסו למצוא איך.

אחרי שהילדים פותרים את החידה הזו, נותנים להם חדשה דומה מאוד, זו:

מה ההבדל המהותי בין שני המקרים? והאם יש שיטה כללית (“אלגוריתם”) שבודקת האם ניתן לצייר במשיכה אחת צורה כלשהי, ואם כן, איך?

התשובה היא שקיימת שיטה שכזו, והיא אפילו פשוטה מאוד. שורש השיטה נעוץ במשפט מפורסם של לאונרד אוילר מתורת הגרפים - אחד מהמשפטים הראשונים, אם לא הראשון, של תורה זו. לפני שניכנס למשפט נציג קודם את המושג של גרף, שהוא ככל הנראה המושג המתמטי המרכזי ביותר במדעי המחשב.

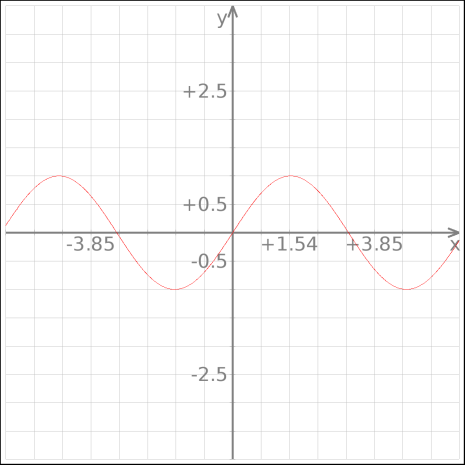
ראשית, צריך להבהיר על מה אנחנו מדברים, כי למילה “גרף” מספר משמעויות שונות, גם במתמטיקה. אנחנו לא מדברים על הדבר הבא:

הדבר שלעיל מכונה “גרף של פונקציה”, והוא אובייקט חשוב בפני עצמו, אבל לא מה שעליו אנחנו מדברים כאן. הגרפים “שלנו” מזכירים מאוד את שתי התמונות למעלה. התמונות הללו הורכבו מקווים ישרים ומנקודות חיבור שלהן (“קודקודים”); גרף פשוט מכליל את המושג והופך אותו לאבסטרקטי יותר.

גרף בבסיסו הוא קבוצה של קודקודים או “צמתים”, שנהוג לסמן באות V, וקבוצה של “קשתות” שמסמנים באות E. כל קשת מחברת שני צמתים בגרף. זהו, זה הרעיון הבסיסי. דוגמאות לא חסר ויש לאלפים. דוגמה מאוד פופולרית היא זו של רשת כבישים בין ערים - כל עיר היא צומת, וכל כביש שמחבר שתי ערים הוא קשת. דוגמה שונה היא עץ משפחה, שבו כל אדם הוא צומת ויש קשת בין כל שני אנשים שהם קרובים מדרגה ראשונה. דוגמה נוספת היא רשת תקשורת - כל מחשב/נתב הוא צומת, ויש קשת בין כל שני צמתים שיש קו תקשורת ישיר שמחבר אותם. גם אתרי אינטרנט הם סוג של גרף - כל דף הוא צומת, ויש קשת בין כל שני דפים שיש לינק מאחד מהם אל השני.

בחלק מהדוגמאות, ובפרט באחרונה, יש הרגשה חזקה מאוד של חוסר סימטריה - הרי ייתכן מאוד שאני אקשר לאתר כלשהו למרות שהוא לא יקשר אלי, אז למה הקשת היא “בין שנינו”? לכן נהוג להבדיל בין שני סוגים עיקריים של גרפים - מכוונים ולא מכוונים. גרף לא מכוון הוא גרף שבו הקשת היא “בין” הצמתים; גרף מכוון הוא כזה שבו כל קשת היא “מצומת א’ אל צומת ב’”, כלומר לכל קשת יש כיוון.

כמובן שייתכן שבין שני צמתים יהיו שתי קשתות, אחת לכל כיוון; אבל באופן כללי לרוב לא מתעסקים בגרפים שבהם יש “קשתות עודפות” (כלומר, שתי קשתות בין זוג צמתים מסויים בגרף לא מכוון, או שתי קשתות מכוונות לאותו הכיוון בין אותם צמתים בגרף מכוון) - אבל כשאני אומר “לרוב”, חשוב להבין שלעתים (לא נדירות עד כדי כך) דווקא כן יש שימוש לקשתות עודפות שכאלו - בפרט, בבעיה שאנו עוסקים בה מותר לדבר על גרפים שכאלו.

עוד משהו שלפעמים מרשים שיהיה בגרף ולפעמים לא הוא קשתות מצומת אל עצמו. לדברים שכאלו קוראים “חוגים עצמיים” - ושוב, אין סטנדרט אחיד שתמיד הולכים לפיו. לפעמים נוח להרשות כאלו דברים, ולפעמים נוח לאסור עליהם, תלוי בשימוש הספציפי שאנו רוצים לעשות בגרף.

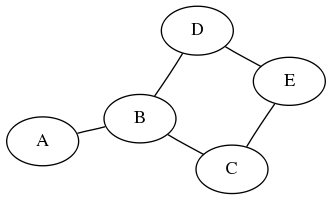
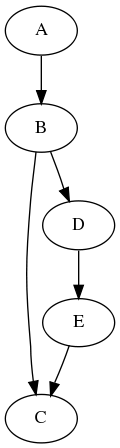
הנה דוגמאות סטנדרטיות לגרפים:

הגרף השני מכוון והראשון לא, אבל פרט לכך אלו בדיוק אותם גרפים; אותם קודקודים (A,B,C,D,E) ואפילו אותן קשתות. אם מוחקים את החצים מהקשתות בגרף השני, מקבלים את הגרף הראשון (אומרים בכזו סיטואציה שהגרף הלא מכוון הוא “גרף התשתית” של הגרף המכוון). זוהי דרך הציור הסטנדרטית והמקובלת של גרפים (למי שתוהה, הגרפים הללו ציורו באמצעות התוכנות שבחבילה graphviz, שמאפשרות ציור אוטומטי של גרפים אם מספקים תיאור סכמטי טקסטואלי פשוט שלהם. מומלץ בחום).

אם כן, הכרנו גרפים. מה הקשר של זה לבין חידת הילדים שלעיל? לצורך כך יש לגרור למשחק עוד מושג אחד שניתן להגדיר על גרפים - מסלול.

מסלול בגרף, באופן די טבעי, הוא פשוט סדרה של צמתים כך שיש קשת בין כל שני צמתים עוקבים בסדרה (ואם הגרף מכוון, אז קשת “בכיוון הנכון”). למשל, בדוגמה שלעיל, A,B,C הוא מסלול. גם C,B,A הוא מסלול תקין בגרף הלא מכוון, אבל בגרף המכוון הוא “נגד הכיוון”. ברמה העקרונית יש לציין בכל מסלול גם על איזו קשת עוברים, אבל כל עוד בין כל שני צמתים יש רק קשת אחת בכל כיוון, המידע הזה ברור.

כמובן שאפשר במסלול לבקר כמה פעמים באותה הצומת. למשל, בגרף הלא מכוון, B,D,E,C,B,D,B,C הוא מסלול מטורלל שכזה. מכאן קצרה הדרך להגדרה של מעגל בתור מסלול שמתחיל ונגמר באותה הצומת, אבל בגרפים לא מכוונים זה יוצר בעיה, כי “מעגל” על פי הגדרה זו יהיה גם מסלול שמתחיל ללכת בכיוון מסויים, “מתחרט” וחוזר על עקבותיו. לכן לרוב עוסקים רק במעגלים ומסלולים “פשוטים” - כאלו שבהם כל צומת מופיע פעם אחת בדיוק, עם היוצא מן הכלל היחיד שלפיו צומת ההתחלה יכול להיות גם צומת הסיום.

לסיום, גרף לא מכוון הוא “קשיר” אם קיים מסלול מכל צומת בגרף לכל צומת אחר בגרף (בגרפים מכוונים התכונה הזו נקראת “קשיר היטב” - לא ניכנס לזה). קל לראות את המשמעות של מסלול וגרפים קשירים בדוגמאות שנתתי - למשל, בגרף שממדל רשת תקשורת מסלול ממחשב אחד לשני מתאר נתיב אפשרי להעברת מידע בין מחשבים, וגרף קשיר הוא גרף שבו כל מחשב מסוגל להתחבר לכל מחשב אחר; בעץ משפחה מסלול ממדל קרבת משפחה וגרף הוא קשיר אם כל האנשים שמתוארים בו הם קרובים זה לזה (בעצי משפחה זה תמיד כך; בפוסטים הבאים אני מקווה להרחיב על עצים ואז נראה שקשירות היא חלק מהותי מההגדרה של עץ).

עכשיו סוף סוף אפשר להציג את הצורה שבה תורת הגרפים עוזרת לפתרון החידה, אבל קודם כל שעת סיפור. מעשה בעיר בשם קניגסברג (קלינינגרד בימינו) בה עבר נהר שחילק את העיר לארבעה חלקים - שתי גדות, אי קטן באמצע, ועוד אי גדול אחר כך, ועל כל המהומה הזו יש שבעה גשרים:

כמובן, טיול בעיר שכזו לא שווה גרוש אם הוא לא כולל מעבר על הגשרים. השאלה היא האם ניתן לטייל בעיר בצורה כזו שבה עוברים על כל הגשרים, אבל לא עוברים על אף גשר יותר מפעם אחת (ולא חוצים את הנהר בשיטות אחרות, כמו קפיצה במוט).

קל לנחש שהתשובה שלילית. קל לנחש, כי אם התשובה הייתה חיובית, כנראה שלא הייתה כאן שאלה והפתרון היה מתגלה יחסית מהר (בדומה לבעיה של משחק ה-15). לרוע המזל, הוכחות של “אי אפשר לעשות את זה” או “קשה לעשות את זה”, שבהן צריך איכשהו לכסות מגוון רחב של דרכי פעולה, הן מסובכות יותר לעתים קרובות מהוכחות היתכנות, שבסך הכל צריכות להראות דרך אחת לא רעה לעשות את זה.

ואז הגיע אוילר. לאונרד אוילר היה אולי המתמטיקאי החשוב ביותר של המאה ה-18, ואחד מהמתמטיקאים הפורים ביותר בכל הזמנים. לצערי, איני יודע מה היה הפתרון המדוייק שלו; אני יודע רק את דרך ההצגה ה”מודרנית” שלו, שמשתמשת במושג הגרף האבסטרקטי שלא היה קיים אז. מה שנאה במיוחד בפתרון של אוילר הוא שהוא לא רק פותר את בעיית הגשרים של קניגסברג, אלא את כל הבעיות מסוגה, ובפרט את שתי בעיות הציור שהצגתי לעיל.

את כל הבעיות הללו ניתן לנסח באופן הבא: בהינתן גרף, האם קיים בו מסלול או מעגל שעובר בכל הקשתות בדיוק פעם אחת? למסלול/מעגל שכזה קוראים “מסלול/מעגל אוילריאני”, לכבודו של אוילר. ברור שבעיית הגשרים של קניגסברג היא בעיה של בדיקת קיום מסלול אוילריאני; כדי לראות שגם בעיות הציור הן כאלה צריך רק לשים לב לכך ש”מסלול אוילריאני” פירושו “ציור קווים מבלי להרים את העפרון מהדף ומבלי לחזור על קו שכבר ציירנו”, כאשר הגרף שלנו מושרה מהצורה - הצמתים הם נקודות החיבור של הקווים, והקווים עצמם הם הקשתות.

מה שנאה במיוחד בפתרון של אוילר הוא שהקריטריון לבדיקת קיום מסלול אוילריאני הוא פשוט ביותר, וניתן לבדיקה על ידי כל ילד. ראשית, הכרחי שהגרף יהיה קשיר; מן הסתם אם הגרף לא קשיר יהיו קשתות שפשוט לא נוכל להגיע אליהן. לכן מגבילים את עצמנו מראש לדיון על גרפים קשירים בלבד (שימו לב שלא אוסרים על כמה קשתות בין אותם צמתים - בגרף שמתקבל מהגשרים של קניגסברג יש דבר שכזה).

הקריטריון של אוילר מתבסס על מושג הדרגה של צומת. דרגה של צומת, בגרף לא מכוון, היא פשוט מספר הקשתות שמחוברות אליו. למשל, בדוגמה שנתתי לעיל הדרגה של A היא 1 והדרגה של B היא 3. הקריטריון הוא כדלהלן: בגרף יש מעגל אוילריאני אם ורק אם הדרגה של כל הצמתים היא זוגית; ויש בו מסלול אוילריאני אם ורק אם לשני צמתים יש דרגה אי זוגית ולכל היתר יש דרגה זוגית.

מה שזה מראה מייד הוא שבעיית הגשרים של קניגסברג לא פתירה, כי הגרף שמתאים לה הוא זה:

ובגרף הזה הדרגה של כל צומת היא 3 פרט לשמאלי ביותר שדרגתו 5, כלומר הקריטריון של אוילר לא מתקיים. באופן דומה, הריבוע עם איקס בפנים גם כן לא מקיים את הקריטריון - אם לא מחשיבים את נקודת החיתוך שבאמצע בתור צומת ויש רק ארבעה צמתים, אז הדרגה של כל אחד מהם היא 3; אם כן מחשיבים אותה כצומת, אמנם מקבלים צומת אחת עם דרגה זוגית 4, אבל הדרגה של שאר הצמתים לא משתנה.

אז למה הבית כן בר-ציור? ראשית, הגג הוא צומת מדרגה 2; שנית, שני הקודקודים העליונים ב”ריבוע” הופכים להיות מדרגה 4 בזכות הגג; לכן נשארים רק עם שני צמתים מדרגה אי זוגית, והגרף כן עונה על קריטריון אוילר - במקרה זה, מובטח לנו מסלול אוילריאני אבל לא קיים מעגל אוליריאני ולכן אנחנו אמנם מסוגלים לצייר את הבית, אבל לא לסיים את הציור בקודקוד שממנו התחלנו. למעשה, כפי שנראה תכף כשאתאר את ההוכחה, הקריטריון אומר שכדי להצליח לצייר את הבית חייבים להתחיל מאחד מהקודקודים בעלי הדרגה האי זוגית, ולסיים את הציור בקודקוד האי זוגי השני.

הנה הוכחה (לא לגמרי פורמלית) של הקריטריון.ראשית נטפל במקרה שבו לכל הצמתים דרגה זוגית. ניקח צומת שרירותי ונתחיל “לטייל” ממנו על הגרף, כשאנחנו מסמנים כל קשת שבה עברנו כדי שלא נעבור בה שוב בטעות. האבחנה המהותית בנוגע לטיול היא זו: כשאנחנו נכנסים לצומת, אנחנו מקטינים את הדרגה שלו ב-1 (כי “מחקנו” את הקשת שנכנסה אליו) וכשאנחנו יוצאים מצומת, אנחנו שוב מקטינים את הדרגה שלו ב-1 (כי “מחקנו” את הקשת שיצאה ממנו). אחרי הצעד הראשון בטיול שלנו, הדרגה של הצומת שממנו התחלנו תהיה אי זוגית (כי קודם היא הייתה זוגית והקטנו אותה ב-1), אבל פרט לכך כל הזמן אנחנו מקטינים דרגות של צמתים ב-2 (כי אנחנו גם נכנסים לצומת וגם יוצאים ממנו) ולכן הדרגות של כל שאר הצמתים נותרות זוגיות.

כעת, מתי הטיול שלנו ייתקע? הטענה היא שאם נתקענו (כלומר, הגענו לצומת שאין לנו יציאה ממנה - דרגתה 0) בהכרח שבנו לצומת שממנו התחלנו. זאת מכיוון שאם אחרי כניסה לצומת דרגתו היא 0, פירוש הדבר הוא שרגע לפני שנכנסו אליו דרגתו הייתה 1 - כלומר בפרט אי זוגית, וזה יכול להיות רק לצומת שממנו התחלנו.

הטיעון שלעיל עשוי בהחלט להישמע כמו “רמאות” אבל הוא תקף לחלוטין. היופי כאן הוא שאיננו צריכים כלל לנסות ולתאר את המסלול שלנו על גבי הגרף או לדרוש ממנו כלום, ועם זאת עדיין מובטח לנו שהוא יכול להיתקע אך ורק בצומת שממנה התחלנו. זו הדגמה נוספת לכוחן של שמורות - במקרה הזה, השמורה של “כל הצמתים בגרף פרט לזה שהתחלנו ממנו הם בעלי דרגה זוגית”.

אם כן, הטיול שלנו בגרף הסתיים במעגל שכיסה לפחות חלק מהקשתות, אבל לא בטוח שאת כולן. אם נמחק מהגרף את הקשתות שכבר עברנו עליהן, נקבל גרף חדש, עם פחות קשתות (אולי אפילו כמה גרפים קטנים יותר כי הגרף יפסיק להיות קשיר) אבל עם אותה תכונה בדיוק - הדרגה של כל צומת היא זוגית. לכן אפשר להפעיל גם על הגרף החדש את השיטה שלנו, למצוא גם בו מעגל, וכן הלאה. בסופו של דבר נמצה את כל הקשתות בגרף ונקבל אוסף של מעגלים בו.

כעת האבחנה היא שניתן “לאחד” שני מעגלים שיש להם צומת משותף; מטיילים על גבי מעגל אחד עד לצומת המשותף, ברגע שמגיעים אליו נכנסים למעגל השני, הולכים לכל אורך המעגל השני ומסיימים אותו חזרה בצומת המשותף, ואז ממשיכים את הטיול במעגל הראשון. לכן אפשר להתייחס לכל שני מעגלים בעלי צומת משותף כאל מעגל אחד. אלא שלא תיתכן סיטואציה שבה יש לנו אוסף של מעגלים כך שהצמתים של כל שני מעגלים זרים, כי מכך ינבע שהגרף אינו קשיר, כי מצומת של אחד המעגלים אין דרך להגיע לצומת של מעגל אחר (אחרת הייתה לנו קשת שמחברת בין שני מעגלים, ולכן צומת משותף לשני מעגלים, והיינו מאחדים אותם). לכן אחרי כל האיחודים אנו מקבלים מעגל אחד שמכיל את כל קשתות הגרף ולא עובר באף אחת מהן יותר מפעם אחת - זהו מעגל אוילריאני, וסיימנו.

כעת הטיפול במקרה של שני צמתים מדרגה אי זוגית הוא טריוויאלי. הגרף הוא קשיר, ולכן ניקח מסלול שמוביל מצומת אחד בעל דרגה אי זוגית, אל השני. כמקודם, “נמחק” כל קשת שעברנו עליה. התוצאה? אחרי המחיקות שהמסלול הזה משרה מקבלים גרף שדרגת כל הצמתים בו זוגית. לכן אפשר לפרק אותו לאוסף של מעגלים, ו”להרכיב” את המעגלים הללו על המסלול בין שני הצמתים האי זוגיים שבנינו בהתחלה, בדרך זהה לזו שבה הרכבנו שני מעגלים, וסיימנו.

לסיום, ייתכן שכבר שאלתם את עצמכם האם מתעניינים גם בשאלה המקבילה - האם קיים בגרף מסלול/מעגל שעובר בכל הצמתים בדיוק פעם אחת. התשובה היא שבהחלט מתעניינים במסלולים שכאלו והם זכו לשם משל עצמם - מסלולים המילטוניים. עם זאת, בניגוד למסלולים האוילריאניים שראינו כי קל, אפילו טריוויאלי לבדוק, לא ידוע שום אלגוריתם יעיל שבודק האם בגרף יש מסלול המילטוני; למעשה, זו בעיה NP-שלמה, כלומר פתרון יעיל שלה יגרור פתרון יעיל של אוסף עצום של בעיות קשות דומות (ולא סביר עד כדי כך שפתרון כזה קיים בכלל).

האם בכך מיצתה תורת הגרפים את השימושיות שלה? בוודאי שלא. אנסה להציג עוד שימושים (שונים מהותית מהשימוש הנוכחי) בפוסטים הבאים.