אוטומטים סופיים ושפות רגולריות

נתקלתי לא מזמן בתוצאה פשוטה אך מקסימה בקומבינטוריקה, שעוסקת באופן שבו ניתן למצוא פונקציות יוצרות לשפות רגולריות. לרוע המזל, כדי להסביר את הקשר צריך להסביר ראשית כל מהן פונקציות יוצרות ומהן שפות רגולריות, ולכן אקדיש לכך את הפוסטים הבאים - בשני המקרים מדובר בנושאים מתמטיים בסיסיים בתחומם ומעניינים מאוד גם בלי הקשר שבינם. אתחיל מהנושא שמוכר לי קצת יותר (לא שאני יכול להתיימר לבקיאות רבה באף אחד מהם) - השפות הרגולריות; זה נושא שניתן לגשת אליו במספר דרכים, ואבחר דרך “חישובית” משהו.

דיברתי כאן בעבר על המודל המתמטי של חישוב - מכונת טיורינג. אין צורך להיכנס שום לפרטי המודל, אלא רק לכך שהוא היה מעין מחשב פרימיטיבי מאוד, ועם זאת חזק מספיק כדי להריץ כל תוכנית מחשב קיימת (אולי לא הכי ביעילות). ה”כוח” של מכונת טיורינג נמדד בדרך כלל בכמות המשאבים שמותר לה להשתמש בה, ושני המשאבים העיקריים הם זמן וזיכרון. קשה להפריד את שני המשאבים הללו זה מזה, בגלל שניתן להשיג שיפור בזמן הריצה אם מגדילים את כמות הזכרון (ומה קורה כשמביאים את הגישה הזו לאבסורד הדגמתי לא מזמן), וגם ניתן לשפר את הזכרון לעתים במחיר זמן ריצה גדול יותר (על כך לא פירטתי ולא אכנס לנושא כעת). לכן דיון בהגבלות סיבוכיות, כדאי שיביא בחשבון את שניהם. אתמקד דווקא במדד הפחות “פופולרי” של סיבוכיות זכרון - הסיבה לכך תתברר בהמשך.

השאלה היא אילו בעיות עדיין ניתן לפתור ככל שאנחנו מצמצמים את צריכת הזכרון של המכונה שלנו. הזכרון שמותר להשתמש בו תמיד נמדד כפונקציה של אורך הקלט, \( n \); ותמיד מתכוונים ל”זכרון העבודה” בלבד - כלומר, לא כוללים את הזכרון שהקלט עצמו דורש. אם מרשים למכונה להשתמש בכמות פולינומית של זכרון (ולא מגבילים את זמן הריצה), התוצאה היא מחלקת הבעיות PSPACE, שהיא ענקית וכוללת את המחלקה P (שנחשבת ל”מחלקת כל הבעיות שניתנות לפתרון בזמן יעיל”), את NP (שעליה פירטתי בעבר) ועוד ועוד. אז כמות פולינומית של זכרון זה יותר מדי; השלב הבא הוא לבצע צמצום דרסטי ולהרשות רק כמות לוגריתמית של זכרון, כלומר רק \( O\left(\log n\right) \) זכרון. בניסוח מילולי לא פורמלי - מותר להשתמש במעט מאוד זכרון ביחס לגודל הקלט. גם במחלקה המצומצמת הזו, שנקראת L, עדיין יש בעיות מעניינות - המפורסמת שבהן היא בעית הישיגות בגרף לא מכוון (האם ניתן להגיע מצומת א’ לצומת ב’ בגרף לא מכוון); ההוכחה לכך שבעיה זו פתירה בזכרון לוגריתמי ניתנה בשנת 2004 על ידי מדען המחשב הישראלי עומר ריינגולד (ממכון וייצמן). עם זאת, אני רוצה לחלוף ביעף גם על פני המחלקה המעניינת הזו ולהמשיך לצמצם - כמה עוד אפשר?

מסתבר שלא הרבה. אפשר לדבר גם על המחלקה של הבעיות שפתירות בזכרון \( O\left(\log\log n\right) \), אבל כל מגבלה חריפה עוד יותר מכך תפיל אותנו אל התחתית - זכרון \( O\left(1\right) \). דהיינו - אם אנחנו מרשים רק כמות זכרון קטנה מאוד מאוד מאוד ביחס לקלט, למשל \( \log\log\log n \), כבר אפשר היה לוותר על זה לחלוטין ולהסתפק בכמות זכרון קבועה מבלי לשנות את קבוצת הבעיות שאנו יכולים לפתור. לא אכנס כרגע להוכחה של הטענה הזו, אבל בהחלט ייתכן שאדבר עליה בפוסט בהמשך, שכן לטעמי היא מעניינת למדי (אם כי לא מסובכת).

אז מעתה ואילך נמקד את הדיון הכי נמוך שרק אפשר - זכרון קבוע. “זכרון קבוע” משמעותו שכמות הזכרון שבה האלגוריתם משתמש אינה תלויה בגודל הקלט בכלל. רק כדי להבין מה זה אומר, למתכנתים שבכם, חשבו על תוכנית שאסור לה לבצע רקורסיות ואסור לה להקצות דינמית זכרון בתוך לולאות, ואסור לה להשתמש במשתנים שגודלם דינמי (כלומר, ספריות של “מספרים שלמים גדולים כרצונך” לא מותרות).

השאלה המעניינת הראשונה היא מה קורה מבחינת סיבוכיות זמן. האם ייתכן שנוכל עדיין לפתור בעיות מסובכות, אם ירשו לנו לרוץ זמן רב מאוד? התשובה (המפתיעה?) שלילית - מסתבר שדי בזמן ריצה לינארי באורך הקלט, \( O\left(n\right) \), כדי לפתור את כל מה שבכלל פתיר בזכרון קבוע. יותר מכך - מספיק שהאלגוריתם יקרא כל ביט בקלט בדיוק פעם אחת, יבצע חישוב כלשהו (בזכרון קבוע ובזמן קבוע גם כן) ואז יעבור לביט הבא - ואחרי קריאת כל הביטים, יעצור ויחזיר את הפלט (במקרה שלנו מדברים על פלט של “כן/לא”, למרות שאפשר לדבר גם על פלטים אחרים). גם זו תוצאה מפתיעה למדי (לדעתי) ואציג אותה שוב מנקודת מבט שונה עוד מעט.

אם כן, אנחנו רוצים לעבור מדיבורים על מכונות טיורינג לדיבורים על מודל חישובי עוד יותר פרימיטיבי - יש לו רק כמות קבועה של זכרון עבודה (שתלויה באלגוריתם שהוא מריץ אבל לא בקלט הספציפי), הוא רץ על הקלט בדיוק פעם אחת באופן סדרתי, ובסוף מחזיר תשובה. למודל המוגבל הזה קוראים אוטומט סופי. ברשותכם, אתאר את האוטומט הזה בצורה יחסית פורמלית, כולל סימונים מתמטיים - הדבר חשוב לתוצאה שאני רוצה לתאר בסופו של דבר. מי שלא אוהב אותיות יווניות יכול שלא להסתכל על המתמטיקה, בינתיים.

השלב הראשון בהגדרה הפורמלית של המודל הוא לפשט עוד יותר את כל עניין זכרון העבודה. במקום לדבר על סרט זכרון עם ראש קורא וכותב, כמו שיש במכונת טיורינג, מסתפקים בלהגיד שיש לאוטומט “מצבים”. אפשר לחשוב על כל מצב כמייצג יחידת מידע בסיסית כלשהי. למשל, אם האוטומט שלנו מנסה לפתור את הבעיה “האם המספר שקיבלת כקלט מתחלק ב-3 ללא שארית?” המצבים שלו יהיו “מה שקראתי עד כה מהקלט הוא מספר שמתחלק ב-3 ללא שארית”, “מה שקראתי עד כה מהקלט הוא מספר שמתחלק ב-3 עם שארית 1”, ו-“מה שקראתי עד כה מהקלט הוא מספר שמתחלק ב-3 עם שארית 2”. מסתבר שדי בשלושת המצבים הללו כדי לפתור את הבעיה. מבחינה פורמלית נוהגים לסמן את קבוצת המצבים של האוטומט באות \( Q \), ואת המצבים עצמם לסמן בסימונים קומפקטיים, למשל \( q_{0},q_{1},q_{2} \) הם המצבים במקרה של האוטומט שלעיל.

כעת ניתן לתאר את הריצה של אוטומט על קלט כלשהו באופן הבא: האוטומט קורא ביט מהקלט (נניח לצורך העניין שהקלט מיוצג בבסיס בינארי). על בסיס הביט הזה, ועל בסיס המצב הנוכחי שלו, הוא “בוחר” מצב חדש לעבור אליו. כך אחרי כל קריאת ביט האוטומט עובר מצב, ואפשר לתאר את החישוב שלו כולו בתור מעבר בין מצבים, עד שלבסוף מסתיים הקלט והאוטומט צריך להחזיר תשובה. כדי לפשט את החיים עוד יותר, מגדירים מראש קבוצה של “מצבים מקבלים” - אם החישוב מסתיים במצב מקבל, האוטומט מחזיר “כן”, אחרת הוא מחזיר “לא”. בדוגמה שלנו, \( q_{0} \) הוא מצב מקבל והשאר לא. את קבוצת המצבים המקבלים מסמנים בדרך כלל באות \( F \).

את האופן שבו האוטומט “בוחר” איך לעבור בין מצבים אפשר לתאר באמצעות פונקציה: \( \delta\left(q,\sigma\right)=p \) אם האוטומט עובר מהמצב \( q \) למצב \( p \) אחרי קריאת התו \( \sigma \). מי שלא אוהב פונקציות יכול לחשוב על זה בתור “טבלת מעברים” שהשורות בה הן המצבים של האוטומט, והעמודות הן התווים האפשריים לקריאה, כך שבתא שבשורה שמסומנת על ידי \( q \) והעמודה שמסומנת על ידי \( \sigma \) כתוב \( p \) אם האוטומט עובר מהמצב \( q \) למצב \( p \) אחרי קריאת התו \( \sigma \).

ייתכן שלחלק מכם פתאום מצלצלת בראש המילה “גרף”. אכן, אפשר לתאר כל אוטומט באופן ציורי בתור גרף. הנה הגרף של האוטומט שתיארתי כאן:

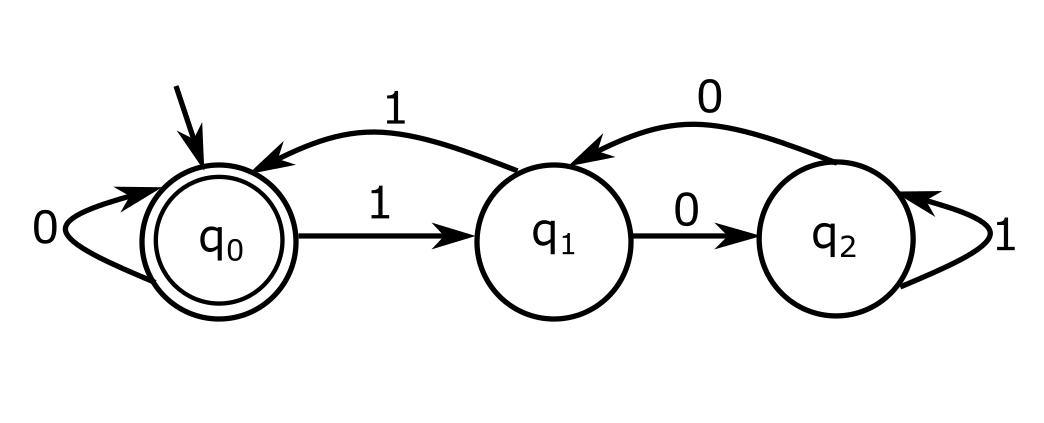
כמו שאפשר לראות, קל מאוד לתאר באמצעות ציור את פונקצית המעברים של האוטומט. חץ שנכנס משום מקום למצב מרמז שזהו המצב ההתחלתי, ומצב שמסומן בעיגול כפול הוא מצב מקבל. עכשיו תוכלו “לשחק” עם האוטומט ולראות שהוא עובד - כתבו מספר כלשהו בבסיס בינארי, “הריצו” את האוטומט על המספר משמאל לימין, כשאתם מתחילים במצב \( q_{0} \), ותראו לאן תגיעו.

אם כן, זהו המודל הבסיסי. המילה “סופי” בשם האוטומט מרמזת שמספר המצבים שלו הוא סופי (מספר מצבים אינסופי יגרום למודל להיות חזק יותר ממכונת טיורינג, ולמעשה - כל יכול מבחינה חישובית). אפשר קצת להקל על ההנחה המובלעת שלי שהאוטומט יודע לעבוד רק על מספרים בייצוג בינארי, ולהרשות לו לעבוד על סדרות של תווים כלשהם מתוך קבוצה סופית מסויימת - לקבוצה שכזו קוראים “אלפבית” ונהוג לסמן אותה באות \( \Sigma \). קלט לאוטומט יהיה סדרה סופית של אותיות מתוך \( \Sigma \) - לסדרה כזו נהוג לקרוא “מילה”, ולאוסף של מילים - “שפה”. המילה “שפה” אולי קצת מטעה כאן - באמצעות סדרות סופיות כאלו של תווים אפשר לתאר דברים רבים ושונים - מספרים שלמים, גרפים, רצפים של DNA, קבצי וידאו, מודל של מערכת השמש וכו’.

לסיום נחזור להערה שהערתי בהתחלה. המודל שתיארתי כאן קורא את הקלט סדרתית, ביט אחרי ביט, ולא חוזר אחורה אף פעם. ניתן להוכיח (וההוכחה אינה פשוטה) שמודל זה שקול למודל שכן מותר לו לחזור אחורה - למעשה, שיכול ללכת קדימה ואחורה כאוות נפשו. במילים אחרות, אין צורך בקריאת כל תו קלט יותר מפעם אחת. זה מוביל מייד למסקנה שאם הגבלנו את כמות הזכרון שלנו ל-\( O\left(1\right) \), אז אין צורך בזמן ריצה גדול יותר מ-\( O\left(n\right) \) (אבל זמן ריצה כזה הוא הכרחי; לפעמים כל תו במילה יכול לשנות התשובה שיש להחזיר עליה, והאוטומט שנתתי לעיל הוא דוגמה לכך, ועל כן חייבים לקרוא את כל הקלט).

אם יש לנו אוטומט, אז אוסף המילים שעליהן הוא אומר “כן” הוא “השפה שמקבל האוטומט”. לשפה כזו, שיש אוטומט סופי שמזהה אותה, קוראים שפה רגולרית. השאלה הראשונה שקופצת לראש היא מהן, אם כן, כל השפות הרגולריות - האם יש להן אפיון פשוט? למרבה השמחה, מתברר שכן. כל שפה סופית היא רגולרית (כי כל מה שצריך לעשות הוא להשוות את מילת הקלט לרשימה סופית ונתונה מראש של מילים - אין צורך בזכרון עבודה שתלוי בגודל הקלט כדי לעשות זאת). אם יש שתי שפות רגולריות, גם איחודן - השפה שהמילים בה הן מילים ששייכות לפחות לאחת משתי השפות המקוריות - הוא רגולרי. בנוסף לכך, יש עוד שתי פעולות הרכבה מתוחכמת יותר שניתן לבצע על שפות כדי לקבל שפה רגולרית.

ראשית, אם יש לנו שתי מילים כלשהן, \( u,v \), אז אפשר לדבר על השרשור שלהן, שמסומן ב-\( u\cdot v \) - זו פשוט מילה שמתחילה ב-\( u \), ואחרי ש-\( u \) נגמרת, מתחילה \( v \). למשל, אם \( u=101 \) ואילו \( v=110 \), אז השרשור שלהן הוא \( u\cdot v=101110 \). כעת אפשר לדבר גם על שרשור של שפות - שרשור שתי שפות \( L_{1},L_{2} \) הוא אוסף כל המילים שהן שרשור של מילה מ-\( L_{1} \) עם מילה מ-\( L_{2} \). בצורה פורמלית, \( L_{1}\cdot L_{2}=\left\{ u\cdot v|u\in L_{1},v\in L_{2}\right\} \).

בעזרת פעולת השרשור אפשר להגדיר גם פעולת “חזקה” - \( L^{i} \) הוא פשוט שרשור של \( L \) עם עצמה בדיוק \( i \) פעמים. ניתן להראות ששרשור של שתי שפות רגולריות הוא שפה רגולרית בעצמו, ולכן גם חזקה כלשהי של שפה תהיה רגולרית. אלא שכל הפעולות הללו הן סופיות במהותן - אם נפעיל אותן על שפות סופיות, נקבל שוב שפות סופיות, אבל הרי יש גם שפות לא סופיות שהן רגולריות, כמו זו בדוגמת ההתחלקות ב-3 שנתתי. אז מה עוד חסר?

הפעולה הנוספת אינה כה מסובכת. כבר הסכמנו שלכל \( i \), החזקה ה-\( i \)-ית של \( L \) רגולרית היא בעצמה רגולרית. אם כן, למה לא לבנות שפה שמורכבת מאיחוד כל החזקות הללו? מכאן מגיעה ההגדרה הפורמלית של “סגור קלייני” (Kleene) \( L^{*}=\bigcup_{i=0}^{\infty}L^{i} \) (\( L^{0} \) מוגדרת בתור שפה שמכילה רק את המילה הריקה - מושג טכני שלא אכנס אליו כאן). ניתן להוכיח כי גם \( L^{*} \) רגולרית אם \( L \) רגולרית (ולעתים אף יותר מכך - תוצאה יפה ומעניינת היא שאם האלפבית של המילים בשפה \( L \) כלשהי מכיל תו בודד, אז \( L^{*} \) תהיה תמיד רגולרית). מה שעוד ניתן להוכיח והוא הפאנץ’ של כל זה הוא שכל שפה רגולרית יכולה להתקבל מהשפות הסופיות על ידי הפעלות נשנות של שלוש הפעולות שהצגתי - איחוד, שרשור וסגור קלייני. האפיון הזה הוא הבסיס לעיסוק בביטויים הרגולריים - עוד נושא שראוי לפוסט נפרד.

אם כן, “שדה המשחק” של השפות הרגולריות הוא יחסית ברור. בדרך כלל הדיון ממשיך מכאן לכיוון מציאת תכונות סגור נוספות ואפיונים נוספים של שפות רגולריות, אך כאמור - אני רוצה לעבור כעת לקומבינטוריקה ולדבר על פונקציות יוצרות. על כך - בפוסט הבא.